[백준] 11722번: 가장 긴 감소하는 부분 수열

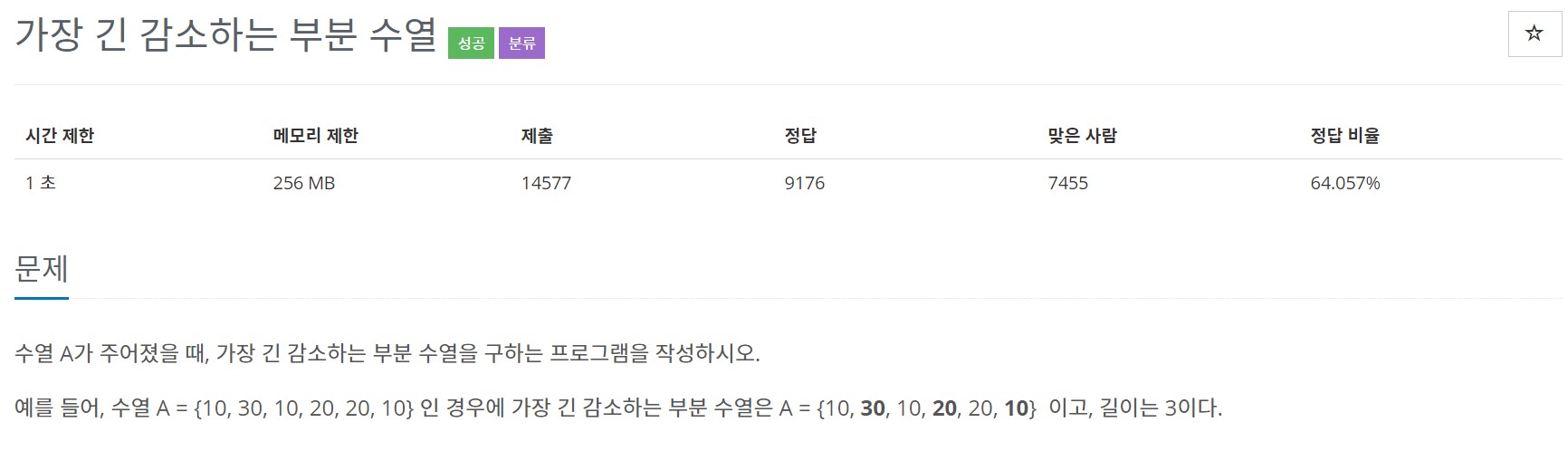
이 문제는 말 그대로 가장 긴 감소하는 부분 수열의 길이를 구하면 된당😝

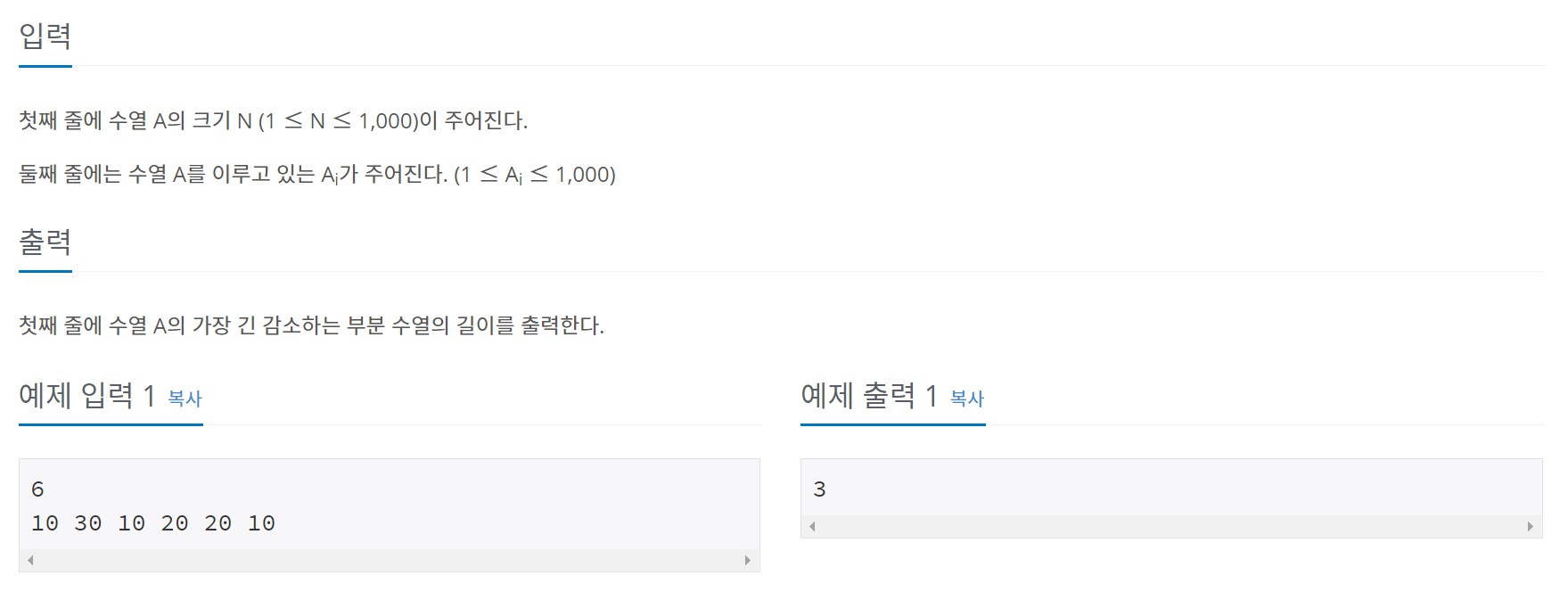
입력으로 들어오는 수열의 크기를 먼저 입력받고 수열이 들어온다. 반복문으로 받으면 된당

아래는 전체 소스코드다🙄

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.Arrays;
import java.util.StringTokenizer;

public class boj11722 {
    public static void main(String[] args) {
        try {
            BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
            BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

            int num = Integer.parseInt(br.readLine());

            int[] seq = new int[num]; // 수열 입력받을 배열
            int[] dp = new int[num]; // dp 배열 - 각 요소까지의 최장 감소수열 길이
            Arrays.fill(dp, 1);

            StringTokenizer st = new StringTokenizer(br.readLine(), " ");
            br.close();
            for(int i = 0; i < num; i++) {
                seq[i] = Integer.parseInt(st.nextToken());
            }

            // dp 계산
            for(int i = 0; i < seq.length; i++) {
                int idx = -1;
                int maxLength = -1;

                for(int j = 0; j < i; j++) {                    
                    if(seq[i] < seq[j] && maxLength < dp[j]) {
                        maxLength = dp[j]; // maxLength 갱신
                        idx = j;
                    }                   
                    if(idx != -1)
                        dp[i] = dp[idx] + 1;
                }
            }
            
            // dp 배열의 최댓값 출력
            int solution = Arrays.stream(dp).max().getAsInt();
            bw.write(Integer.toString(solution));
            bw.flush();
            bw.close();

        } catch (Exception e) {
            e.printStackTrace();
        }

    }
}

여기서 dp계산은 아래의 반복문에서 이뤄진다🤭
수열의 원소 별로, 차례로 값을 계산한다🤗
dp[i] 👉🏻 부분 수열 seq(0,i) 내의 가장 긴 감소하는 수열의 길이.

for(int i = 0; i < seq.length; i++) {
    int idx = -1;

    // maxLength는 검사하는 원소 이전의 가장 긴 감소하는 수열의 길이임
    int maxLength = -1;

    for(int j = 0; j < i; j++) {
        // 감소하는 수열: seq[i]가 seq[j]보다 작아야함.
        // 그리고 maxLength가 가장 긴 인덱스를 idx에 저장한다.
        if(seq[i] < seq[j] && maxLength < dp[j]) {
            maxLength = dp[j]; // maxLength 갱신
            idx = j;
        }
        // idx가 -1이 아니면 (= 최장 비내림차순 수열 길이가 바뀌었으면)
        if(idx != -1)
            dp[i] = dp[idx] + 1;
    }
}

내가 실수 했던 부분이 있는데, maxLength를 반복문 내에서 1로 초기화했던 것이다. 내가 dp를 전부 1로 초기화해서, 원소별로 maxLength와 비교했을 때 갱신이 이뤄지지 않았고, idx가 그대로 -1이어서 dp[i] = dp[idx] + 1; 이 실행되지 않았다.

사소한 실수였는데 꽤나 기억에 남을 거 같다. 하하

---

2020.03.30 수정

내가 왜 저렇게 풀었는지 모르겠다.
일단 자바로 쓴 코드에서 잘못한 부분이 있었다.

for(int j = 0; j < i; j++) {                    
    if(seq[i] < seq[j] && maxLength < dp[j]) {
        maxLength = dp[j]; // maxLength 갱신
        idx = j;
    }                   
    if(idx != -1)
        dp[i] = dp[idx] + 1;
}

대체 왜 dp[i]를 for j 안에서 계속 갱신한거냐구..ㅎ

그래서 파이썬 코드에서는 j 반복 끝내고 나서 갱신해주었다.

N = int(input())
A = list(map(int, input().split()))
dp = [1]*N

for i in range(1, N):
    idx = -1
    maxLength = -1
    for j in range(i):
        if A[j] > A[i] and dp[j] > maxLength:
            maxLength = dp[j]
            idx = j
    if idx != -1:
        dp[i] = dp[idx] + 1

print(max(dp))

파이썬으로 다시 풀면서 짜증났던 부분이 마지막에 max(dp)로 답을 내는 거.. 였다.

결국에는 이런식으로 ans 변수를 둬서 마지막에 최댓값을 찾을 필요는 없게 수정했다. 하지만 더 좋은 방법이 있을 것 같은데 어떤 방식을 써야 답을 dp[N-1]로 만들 수 있을지 모르겠다.

N = int(input())
A = list(map(int, input().split()))
dp = [1]*N

ans = 1
for i in range(1, N):
    idx = -1
    maxLength = -1
    for j in range(i):
        if A[j] > A[i] and dp[j] > maxLength:
            maxLength = dp[j]
            idx = j
    if idx != -1:
        dp[i] = dp[idx] + 1
        ans = max(dp[i], ans)
        # 이렇게 하면 dp[N-1]이 최댓값이 되지 않을 때에도
        # 답을 한 번에 낼 수 있다.

print(ans)

더 찾아봐야겠다.