본 포스팅은 제가 읽었던 논문을 간단하게 정리하는 글입니다. 논문의 모든 내용을 작성하는 것이 아닌, 일부분만 담겨 있으므로 자세한 내용은 원본 논문을 확인해 주시기를 바랍니다. 또한, 논문을 잘못 이해한 부분이 있을 수 있으므로, 양해 바랍니다.

1. Introduction

이미지 생성을 위한 Generative Adversarial Networks (GAN)이 등장한 후, GAN은 많은 발전을 이루었음. 이미지 생성 GAN만큼은 아니지만, 시계열 데이터 (time series data) 생성 GAN 또한 발전을 이루었음.

본 논문에서는 시계열 데이터 생성에 적용된 GAN (time series GAN)에 대하여 조사함. 다양한 GAN 아키텍처와 함께, GAN을 적용할 수 있는 문제 상황, GAN 사용 시 고려해야 하는 프라이버시 문제 등을 소개함.

GAN은 진짜 데이터와 유사한 합성 데이터를 생성하는 네트워크로, 다양한 현실 문제에 적용될 수 있음. 한 가지 예시는 data shortage 문제임. 크기가 작은 데이터셋에 GAN을 적용하여 새로운 데이터를 생성, 데이터 증강(augmentation) 효과를 얻을 수 있음.

또한, 데이터가 누락되거나 더럽혀진 (corrupted) 경우, GAN을 활용하여 데이터를 대체할 수 있음. 노이즈 등을 제거하거나 누락된 값을 그럴듯한 값으로 채워 넣어 데이터의 품질을 향상시킴.

이렇게 GAN은 다양한 곳에 적용될 수 있지만, Data protection & privacy 측면에서 주의해야 할 점이 있음. 특히 의료 관련 데이터와 같이 개인의 민감한 데이터를 생성하는 GAN이라면, GAN의 출력을 보고 원본 데이터를 추정할 수 없어야 함. 이는 아래 7. Privacy 섹션에서 보다 자세히 다룸.

아래 2. Related Work에서는 GAN review와 관련된 논문 소개를, 3. Generative Adversarial Networks에서는 기초적인 GAN 관련 배경지식을 소개함. 4. Taxonomy of Time Series based GANs에서는 시계열 데이터와 관련된 다양한 GAN 아키텍처를 소개하며, 5. Applications, 6. Evaluation Metrics, 7. Privacy에서는 각각 시계열 GAN을 적용할 수 있는 분야, 생성된 시계열을 평가할 수 있는 지표, GAN 사용 시 고려해야 하는 프라이버시 문제에 대하여 소개함.

2. Related Work

GAN, 특히 이미지 생성 GAN이 많은 발전을 이룬 만큼 수많은 GAN review paper가 발표되었음. 하지만 대다수의 review paper가 computer vision domain에 초점이 맞춰져 있어 time series GAN 관련된 조사가 부족함.

본 논문은 time series GAN에 초점을 맞춘 첫 번째 review paper임. Time series GAN 관련된 다양한 아키텍처, 손실 함수, 평가 지표, trade-off 등을 소개함.

3. Generative Adversarial Networks

이번 섹션에서는 GAN과 관련된 기본적인 배경지식을 소개함.

3.1 Background

GAN은 기본적으로 두 개의 neural network, Generator $G$ 와 Discriminator $D$ 로 구성됨.

Generator $G$는 random noise $z \in \mathbb R^r$를 입력받아 훈련 데이터 분포와 유사한 합성 데이터(synthetic data)를 생성함. Discriminator $D$는 입력받은 이미지가 진짜 데이터(훈련 데이터)인지, 합성 데이터인지 구분함.

$G$의 목표는 $D$를 속일 만큼 진짜 같은 합성 데이터를 생성하는 것이고, $D$의 목표는 $G$에서 생성한 합성 이미지를 잘 구분하는 것임. 아래의 Figure 2는 전체적인 GAN 아키텍처를 보여줌.

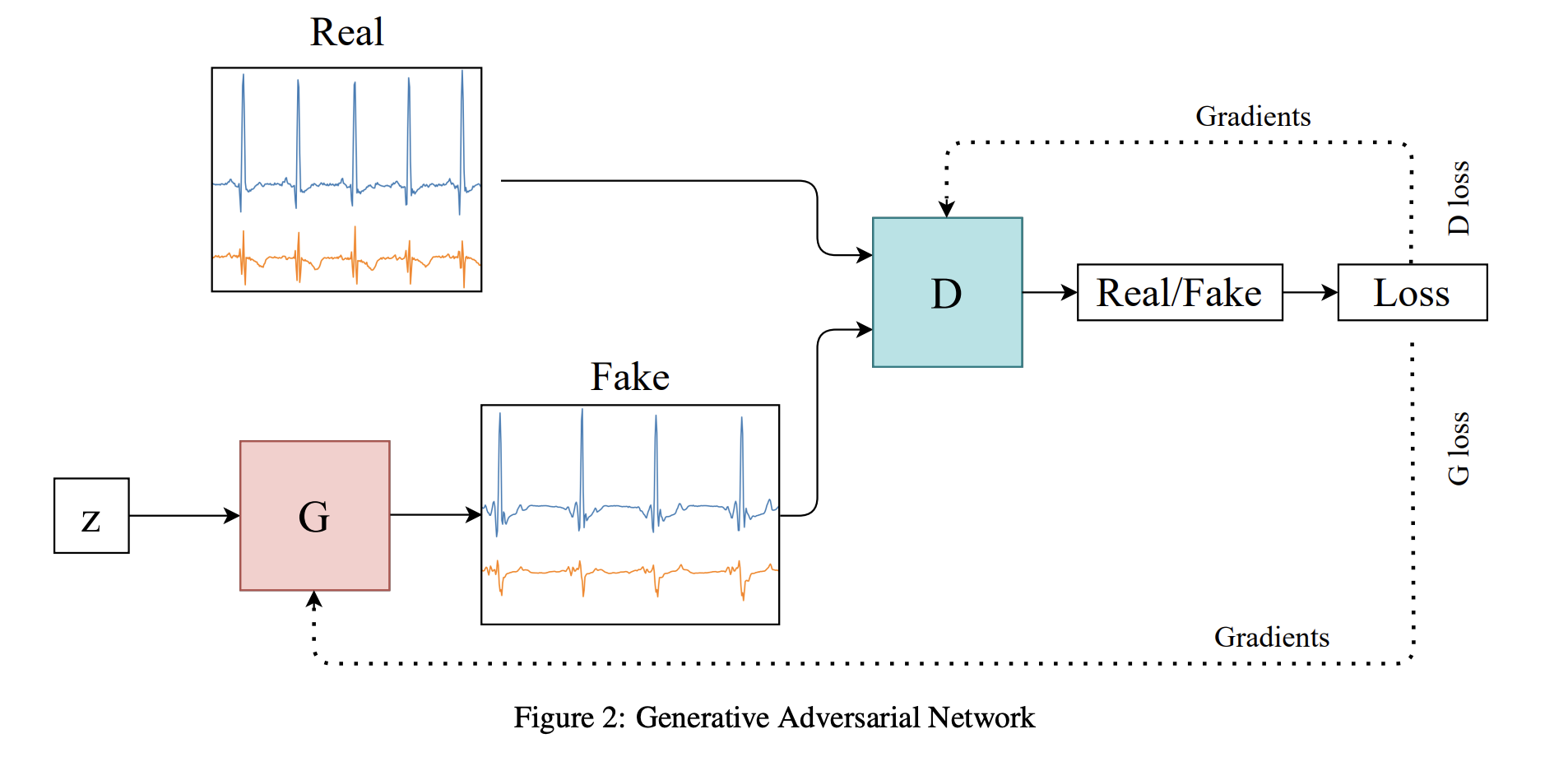
GAN은 아래의 목표 함수를 통해 학습을 진행함. 각 network가 하나의 player가 되어, minmax 게임을 수행함. $D(\mathbf x)$는 이미지 $\mathbf x$를 입력받았을 때 Discriminator가 출력한 진짜 이미지일 확률임.

Ian Goodfellow가 발표한 최초의 GAN은 $G, D$ 네트워크 모두 multi-layer perceptron으로 구현되었음. 이후 deep convolutional layer를 사용한 DCGAN 등 다양한 GAN variants가 발표되었음.

3.2 Challenges

GAN에는 크게 아래와 같은 3가지의 주요 문제가 존재함.

이번 섹션에서는 수학적 개념이 조금 필요합니다.

이렇게 따로 표시된 부분에 대한 보다 자세한 설명은 아래 Appendix에서 확인하실 수 있습니다.

Training stability
GAN 훈련에 대한 global optimality와 convergence는 이미 처음 논문에서 증명되었음.

$V(D^*, G)$를 최소화하는 것이 $D_{JS}(p_{data} \Vert p_g)$를 최소화하는 것과 동일하다는 것을 뜻합니다. $p_r = p_{data}$ 입니다.

Global optimality가 증명되었지만, GAN을 훈련할 때는 vanishing gradients 문제와 mode collapse 문제가 발생할 수 있어 훈련이 매우 불안정함.

식 (1)에서 소개된 식을 그대로 훈련에 사용하면 vanishing gradients 문제가 발생할 수 있음. 만약 $D$가 optimality에 도달하면, $G$에 대한 식 (1)은 Jensen-Shannon (JS) divergence를 최소화하는 것으로 정리됨.

JS divergence는 두 분포 $p_r, p_g$ 사이에 overlap이 없을 때 상수 값($log2 = 0.693$)을 가지며, 이는 $G$ 학습에 사용되는 gradient 값이 0임을 의미함. None-zero gradient가 있기 위해서는 $p_r, p_g$ 사이에 어느 정도의 overlap이 존재해야 함.

실제로 초기의 $G$가 생성하는 이미지는 실제 이미지와 상당히 다를 것이므로, $G$ 학습을 위한 gradient가 매우 작아 학습에 어려움이 있음. 이러한 문제를 보완하고자, $G$에 대한 loss 식을 다음과 같이 변경함.

위의 식은 $\mathbb E_{\mathbf x \sim p_g} \log [D(\mathbf x)]$를 최대화하는 것과 동일함. 식 (1)과 비교하면, $\log (1 - D(\mathbf x))$을 최소화하는 것에서 $\log D(\mathbf x)$을 최대화하는 것으로 식이 수정되었음.

아래의 그림은 $\log x$(빨간색), $\log (1-x)$(파란색)의 그래프를 그린 것임.

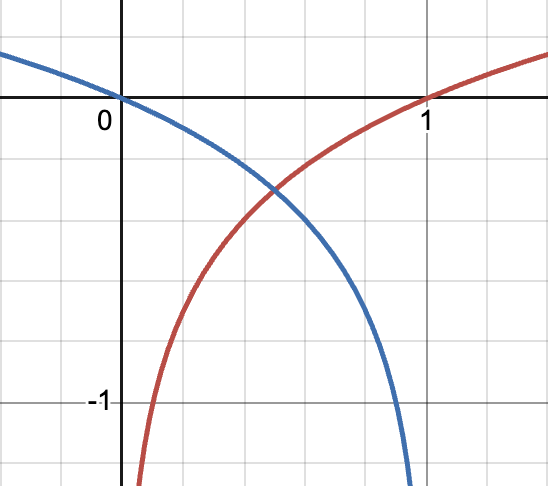
초기 $G$의 출력은 진짜 이미지와 많이 다르기 때문에, $D$가 판별하기 쉬울 것임. 따라서, $D(\mathbf x_{fake})$의 값이 0에 가까움. 위의 그래프를 보면, $x=0$ 근방일 때 $\log x$의 기울기(gradient)가 $\log (1-x)$의 기울기보다 훨씬 큰 것을 확인할 수 있음. 이는 $G$ 학습을 위한 gradient가 식 (3)을 사용할 때 더 큰 것을 의미함.

위와 같이 $G$에 대한 손실 함수를 개선함으로 vanishing gradients 문제를 어느 정도 보완할 수 있음. 하지만, 식 (3)은 mode collapse 문제를 야기하기도 함.

식 (3)을 최적화하는 것은 reverse KL divergence $D_{KL}(p_g \Vert p_r)$을 최소화하는 것으로 정리됨. Reverse KL divergence를 사용하여 최적화할 경우, $p_r$이 여러 개의 mode를 가지고 있을 때 $p_g$가 하나의 mode에 수렴하는 mode collapse 문제가 발생할 수 있음. 이는 아래의 그림에서 오른쪽 경우에 해당함. ($p(x) = p_r$, $q^*(x) = p_g$)

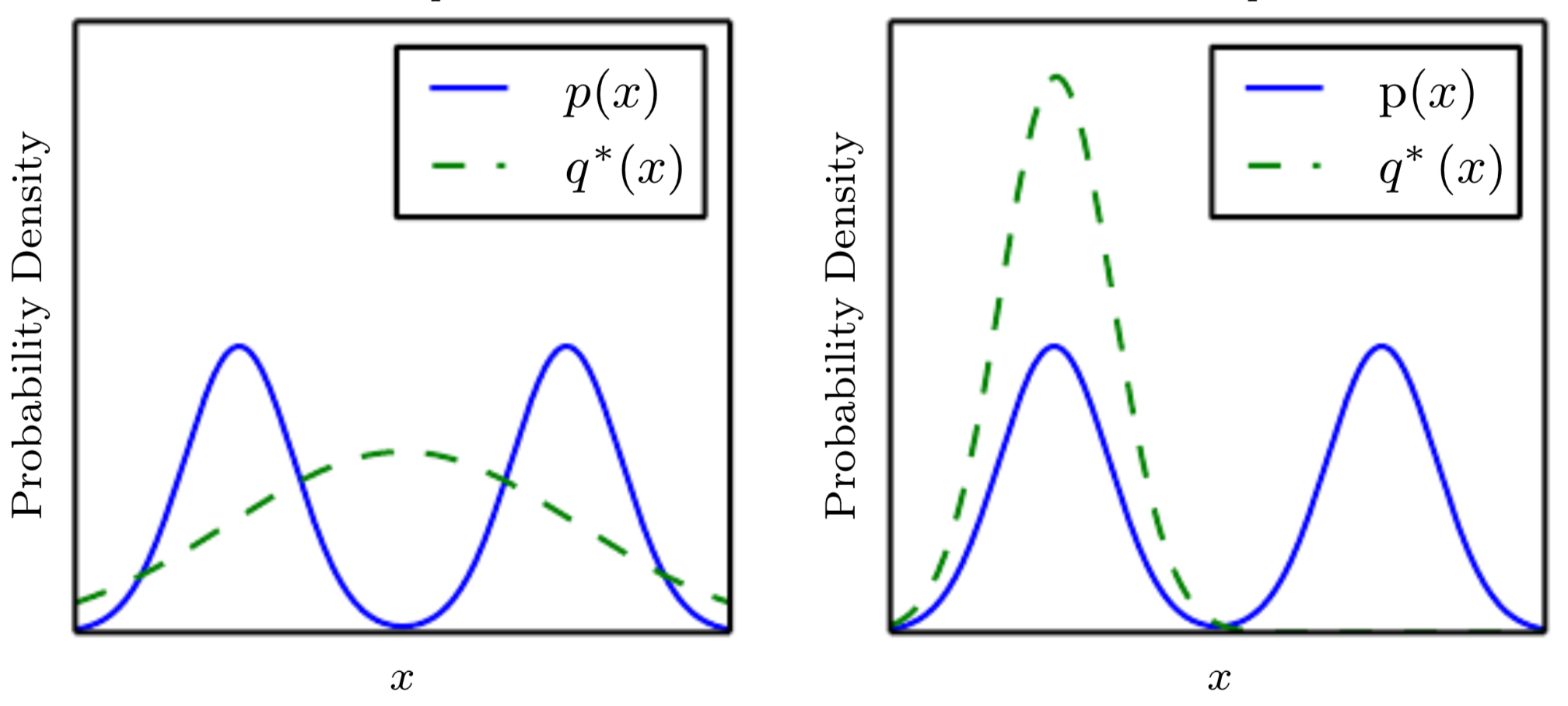
[이미지 출처]

이는 $G$가 실제 데이터 클래스 중 일부 클래스만 생성하는 것으로 이해할 수 있음. 훈련 데이터셋에 개, 고양이, 코끼리 이미지가 있을 때 $D$를 잘 속일 수 있는 고양이 이미지만 생성하는 것임. 이러한 문제는 모델의 아키텍처나 손실 함수 등 근본적인 구조를 개선해야 함.

자세한 증명은 Appendix를 참고해 주세요.

Evaluation
GAN의 성능을 평가하기 위한 다양한 평가 지표가 제안되었음. 평가 지표는 생성된 데이터의 정량적인 부분과 정성적인 부분을 평가함. 이미지 생성 GAN의 경우, maximum mean discrepancy (MMD), Inception Score, Fréchet Inception Distance (FID) 등 다양한 지표가 제안되었음.

시계열 생성 GAN의 경우, 시계열 데이터의 특성상 사람을 통한 정성적인 평가가 어려움. 즉, 생성된 샘플을 보고 진짜 데이터와 얼마나 유사한지 평가하기 어려움. 시계열 데이터에 대한 정성적 평가의 경우 t-SEN, PCA를 사용하여 원본 데이터 분포와 얼마나 유사한지를 비교하며, 정량적 평가의 경우 two-sample test를 수행할 수 있음.

Privacy risk
GAN이 생성한 데이터의 품질을 떠나, GAN이 생성한 데이터와 관련된 프라이버시 문제 또한 반드시 고려되어야 함.

일반적인 비식별화 기술로는 공격자가 추가 데이터를 사용하여 개인을 재식별화하는 것을 막을 수 없다고 연구된 바가 있음. 의료 청구 기록이 비식별화되어 저장된 공개 데이터셋에서, 암호화되지 않은 부분과 개인에 대한 알려진 정보를 사용하여 개인을 재식별한 연구 결과 또한 존재함.

공개된 데이터셋에 대한 재식별화 기술은 건강 정보 등 개인의 민감한 정보를 유출할 수 있으므로, 데이터 생성 시 이 부분을 반드시 고려해야 함. GAN의 경우, 생성된 데이터를 통해 특정 개인이 원본 데이터에 포함되었는지 등 원본 데이터를 추정할 수 없도록 추가적인 방법을 고안해야 함.

3.3 Popular Datasets

Computer vision domain의 경우 CIFAR, MNIST, ImageNet 등 standard benchmarking dataset이 존재하나, 시계열 데이터 생성의 경우 이러한 대표 데이터셋이 존재하지 않음.

이는 time series GAN의 경우 각 문제마다 상황 및 제약 조건이 달라, 모델이 생성하는 시계열의 길이 등 기대하는 출력의 형태가 모두 다르기 때문임. 생성하는 출력 형태가 모두 다르므로, 이를 모두 고려하며 평가할 수 있는 데이터셋이 아직 존재하지 않음.

아래 Table 1은 시계열 데이터 생성에서 자주 사용되었던 데이터셋을 정리한 것임.

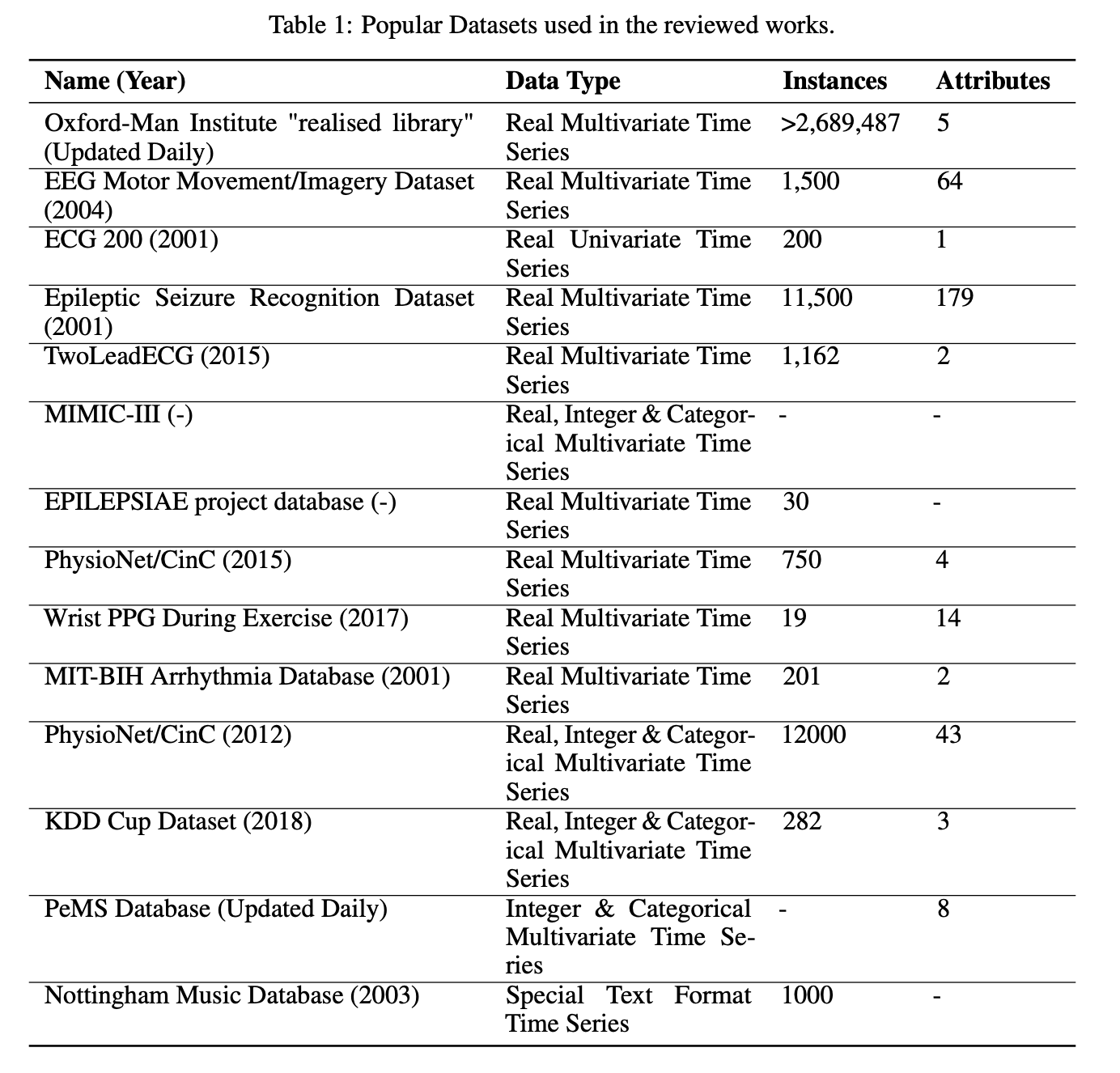
4. Taxonomy of Time Series based GANs

본 논문에서는 time series GAN을 크게 discrete variants와 continuous variants로 분류하였음.

Discrete variants의 경우, Figure 3의 왼쪽과 같이 discrete value를 생성함. Text generation 또한 discrete variants에 속함. Continuous variants의 경우, Figure 3의 오른쪽과 같이 continuous value를 생성함.

Challenges with discrete time series generation
Discrete data를 생성하는 경우, discrete object의 분포가 미분 불가능하여 direct gradient가 없다는 문제가 있음. 이러한 문제는 역전파를 통해 단독으로 $G$를 학습시킬 수 없게 함.

Discrete data의 대표적인 예시는 단어 토큰임. 두 단어 "apple", "banana"가 있을 때, 단어 apple과 banana 사이의 공간은 의미 없는 공간임. 즉, apple의 gradient를 조금씩 업데이트하여 banana에 도달할 수 없음. 어떠한 연속적인 값 $x$가 있을 때, $x + 0.01$ 등의 과정을 반복하여 원하는 값으로 도달할 수 있지만 (gradient descent), $\text{apple} + 0.01$ 등의 연산은 수행할 수 없음.

이러한 문제로 인해 discrete data 생성 시 직접적인 gradient 계산 방식으로 모델을 훈련할 수 없음. 강화 학습, policy gradient 등 다른 방법론을 사용하여 Generator를 학습시켜야 함.

Challenges with continuous time series generation
시계열 데이터의 경우, 시간의 흐름뿐만 아니라 다른 특성에 영향을 받을 수 있음. 심전도 데이터(ECG)의 경우, 각 환자의 나이, 성별, 건강 상태 등 다양한 요소에 의해 영향을 받으므로 이러한 특성을 고려할 수 있어야 함.

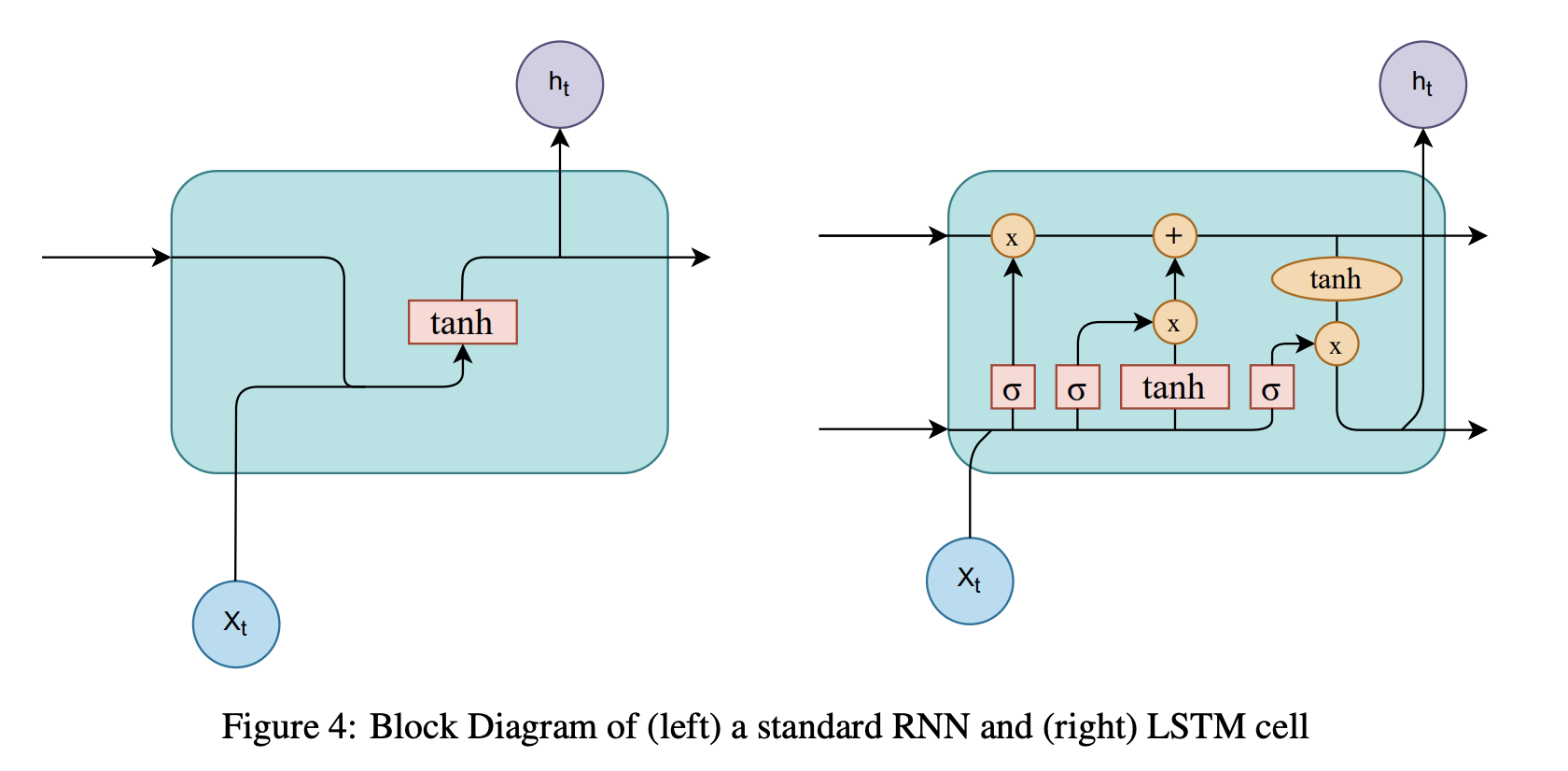
Figure 4의 Recurrent neural networks(RNNs)는 sequential data를 모델링할 때 주로 사용되는 딥러닝 아키텍처임. 내부의 loop-like structure로 인하여 sequential data의 특성을 잘 포착할 수 있음.

Figure 4 왼쪽의 vanilla RNN 보다는 Long-term dependency를 보다 잘 모델링하기 위하여 GRU, 혹은 Figure 4 오른쪽의 LSTM 등 발전된 RNN 아키텍처를 주로 사용함.

RNN 기반의 아키텍처는 sequential data, 즉 time series data 모델링에 적절하므로 많은 time series GAN에서 RNN cell을 사용하여 시계열 데이터를 생성하고 판별하였음.

4.1 Discrete-variant GANs

Sequence GAN (SeqGAN)

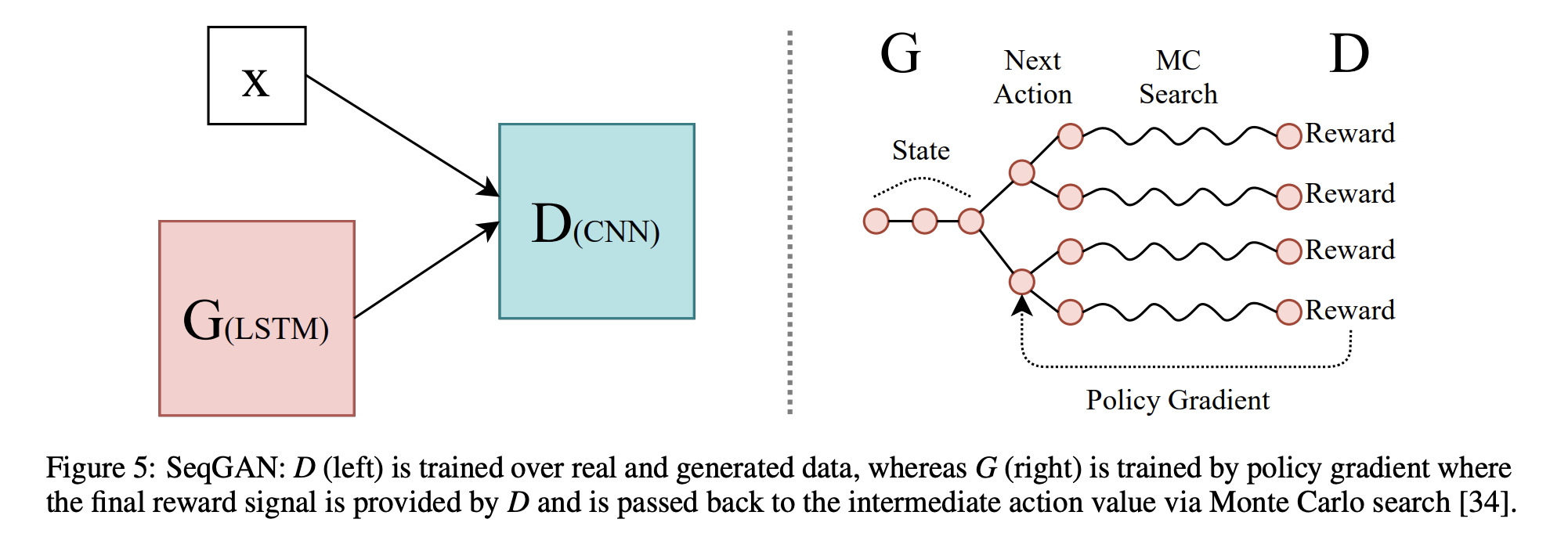
2016년 9월에 발표된 SeqGAN은 time series data에 GAN을 적용한 최초 연구 사례임. SeqGAN은 기존의 generative modeling 방법을 뛰어넘는 성능을 보여주었음. LSTM을 generator로, CNN을 discriminator로 사용하였으며 generator는 단어 토큰을 생성하도록 학습되었음.

앞서 언급하였듯, discrete time series generation에서는 direct gradient를 계산할 수 없음. 따라서, SeqGAN은 policy gradient와 MC(Monte Carlo) Seach를 사용하였음. Generator $G$는 강화학습을 통해 학습되며, Discriminator $D$로부터 받는 보상을 최대화하도록 학습됨. $D$는 입력받은 데이터가 진짜 같다면 positive reward를 제공함.

MC Search는 알파고에 사용되었던 탐색 알고리즘으로, $G$가 단어 토큰을 생성할 때마다 미래의 가능한 시퀀스를 계산한 다음 $D$로부터 예상되는 보상을 계산함. 이후 가장 높은 보상을 얻을 것으로 예상되는 시퀀스를 선택하여 다음 토큰을 생성함.

Quant GAN

2019년 7월에 발표된 Quant GAN은 금융 시계열 데이터에서의 long-range dependencies를 모델링하기 위하여 제안되었음. Generator, Discriminator 두 네트워크 모두 dilated causal convolutional layer를 사용하는 Temporal Convolutional Networks (TCN) 구조임.

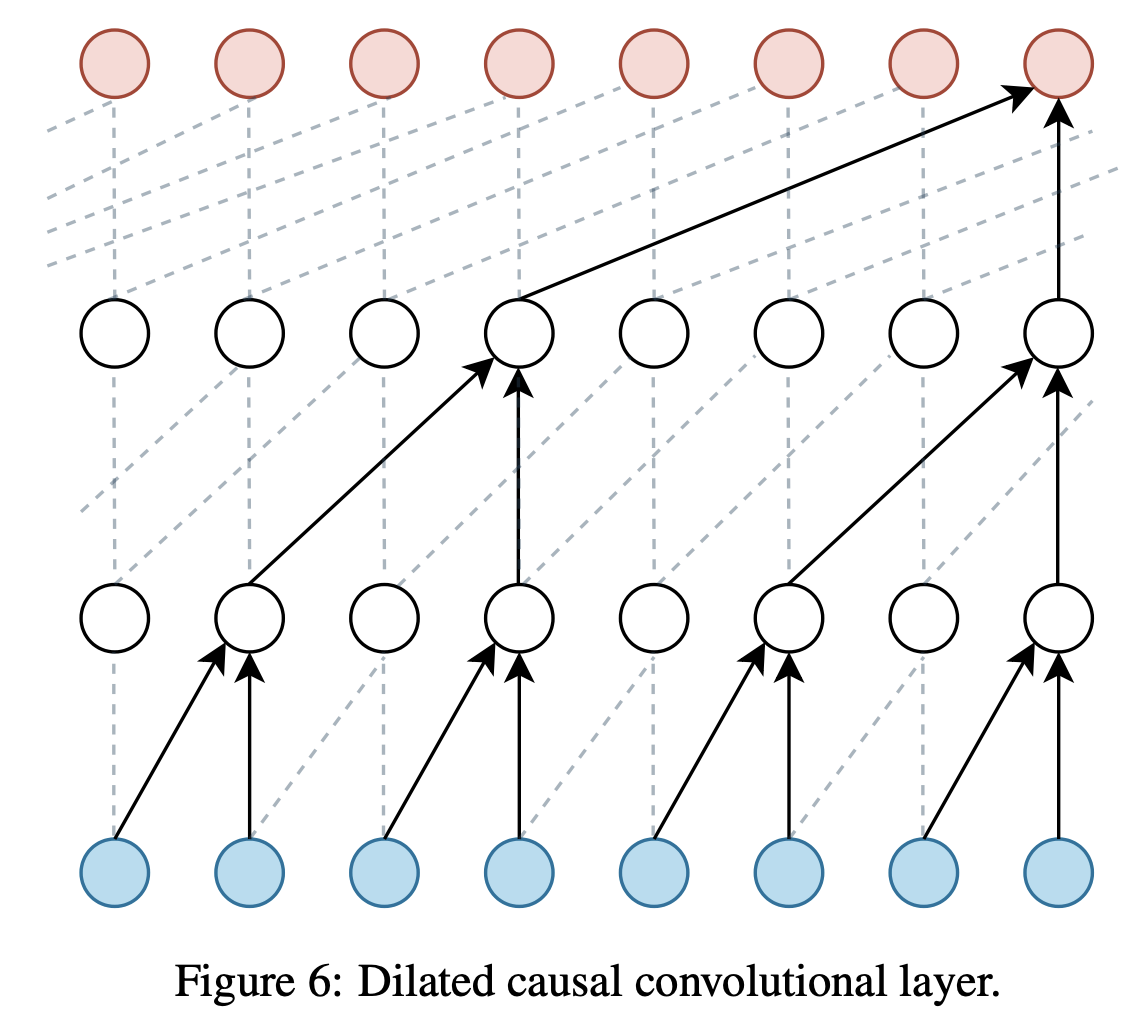
Dilated causal convolutional layer는 위의 Figure 6과 같이 convolution filter의 간격을 조절하고, 미래의 입력을 참고하지 못하도록 조절한 convolutional layer를 의미함. RNN과 함께 시계열 데이터를 모델링할 때 주로 사용되는 딥러닝 아키텍처임.

Figure 6과 같이 두 개의 dilated causal conditional layer를 가지는 $G$는 TCN을 통해 시계열 데이터의 volatility, drift component를 생성함. Quant GAN은 2009년부터 2018년 사이의 S&P 500 주가 데이터로 훈련되었음.

4.2 Continuous-variant GANs

Continuous RNN-GAN (C-RNN-GAN)

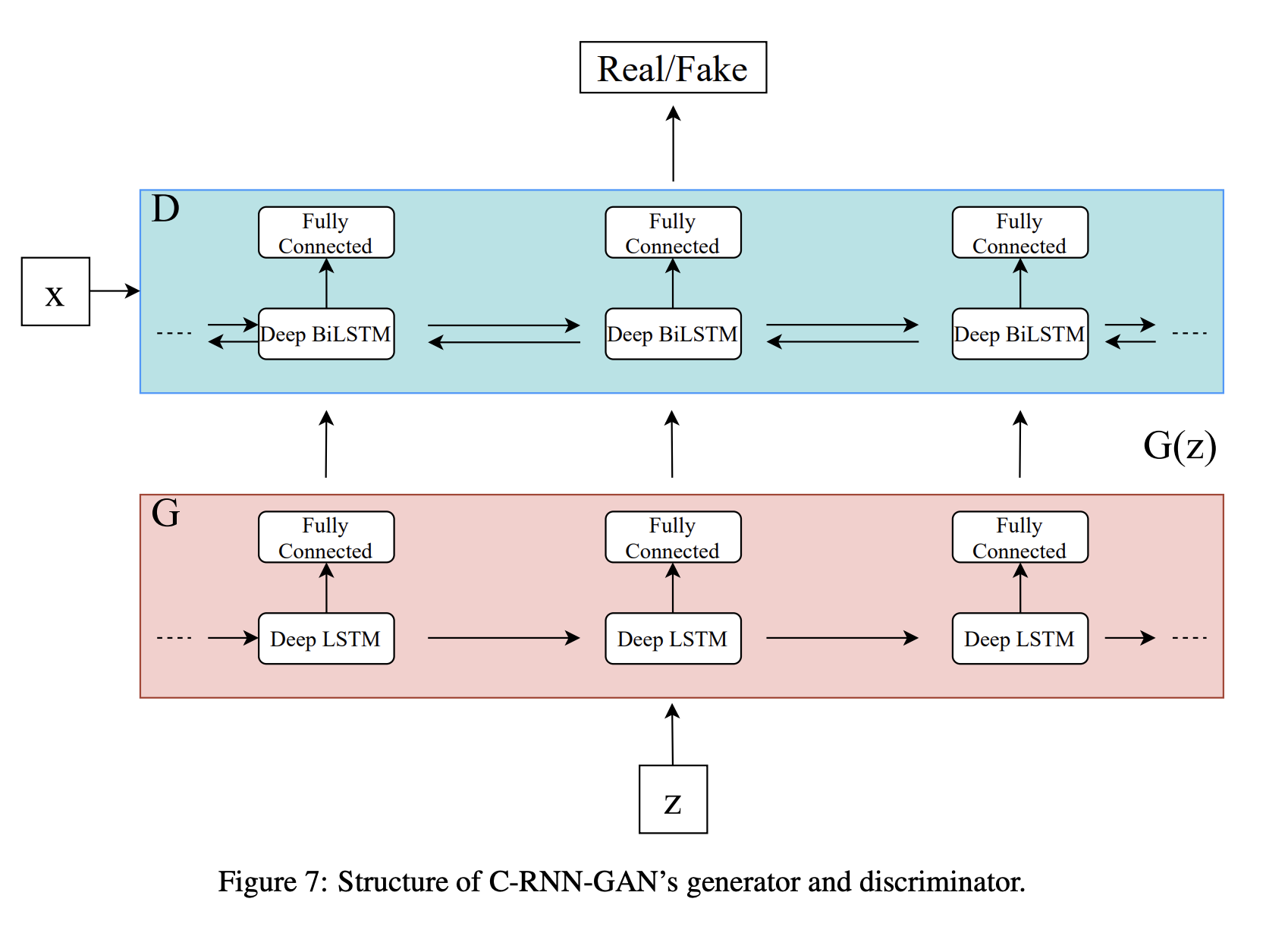
2016년 11월에 발표된 C-RNN-GAN은 GAN을 사용하여 continuous sequential data를 생성한 첫 번째 연구 중 하나임. 다양한 클래식 음악 작곡가의 미디 파일에서 학습되었음.

C-RNN-GAN의 generator는 RNN이며, discriminator는 bidirectional RNN을 사용하였음. 사용된 RNN은 2개의 LSTM layer가 연결된 형태이며, 각 LSTM cell은 350개의 hidden unit을 가지고 있음. Generator $G$는 uniform random vector $z^{(i)}$를 입력받아 sequence를 생성함.

C-RNN-GAN은 backpropagation through time(BPTT) 알고리즘을 통해 훈련되었으며, L2 정규화가 적용되었음. $G, D$ 네트워크 중 한 네트워크가 다른 네트워크에 비해 성능이 너무 좋아지면 freezing을 적용하여 두 네트워크 사이의 밸런스를 조절하였음.

Recurrent Conditional GAN (RCGAN)

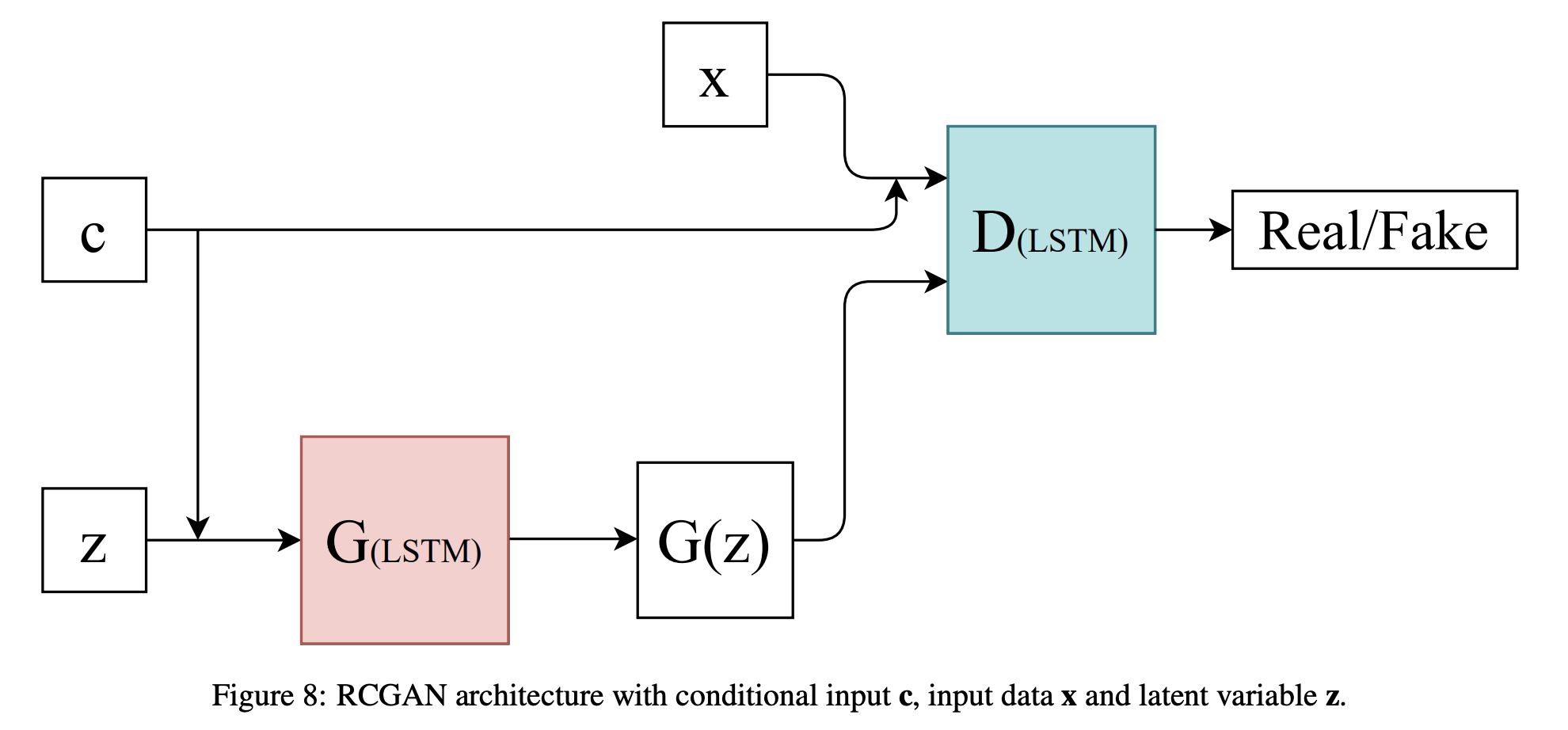
2017년에 발표된 RGAN, RCGAN(RGAN + Condition)은 C-RNN-GAN과 유사하게 LSTM cell을 사용하였지만, unidirectional LSTM을 Discriminator 사용하고 Generator $G$의 출력이 다음 time step에 입력되지 않는다는 등 몇 가지 차이점이 존재함.

[출처 : Esteban, Cristóbal, Stephanie L. Hyland, and Gunnar Rätsch. "Real-valued (medical) time series generation with recurrent conditional gans." arXiv preprint arXiv:1706.02633 (2017).]

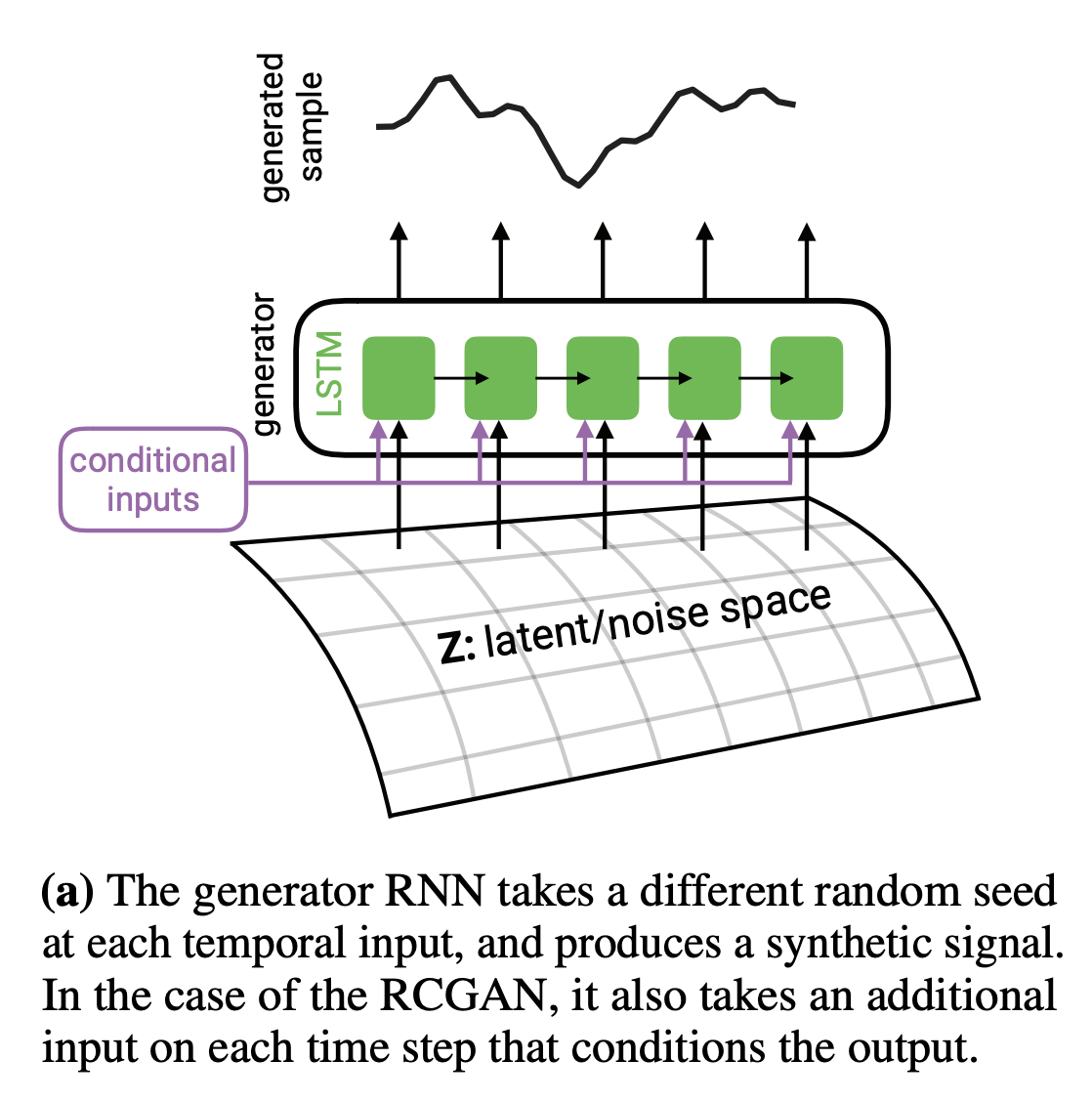
위의 그림과 같이, 각 time step $t$ 마다 $G$는 새로운 random seed(noise)를 입력받아 sequence를 생성함. 하나의 seed(noise, $z$)를 받아 전체 데이터를 생성하는 이전의 모델과 차이점이 있음.

RGAN, RCGAN의 목적은 downstream task에 적용할 수 있는 continuous medical data를 생성하는 것이며, 이는 continuous medical data generation 관련 첫 번째 연구임.

Conditional case(RCGAN)의 경우, Conditional VAE, Conditional GAN과 같이 conditional information $c_n$이 $D, G$에 입력됨. 해당 논문의 저자들은 RCGAN 아키텍처와 함께 해당 모델을 평가할 수 있는 새로운 평가 지표 $\text{MMD}^2$을 제안하였음.

Sequentially Coupled GAN (SC-GAN)

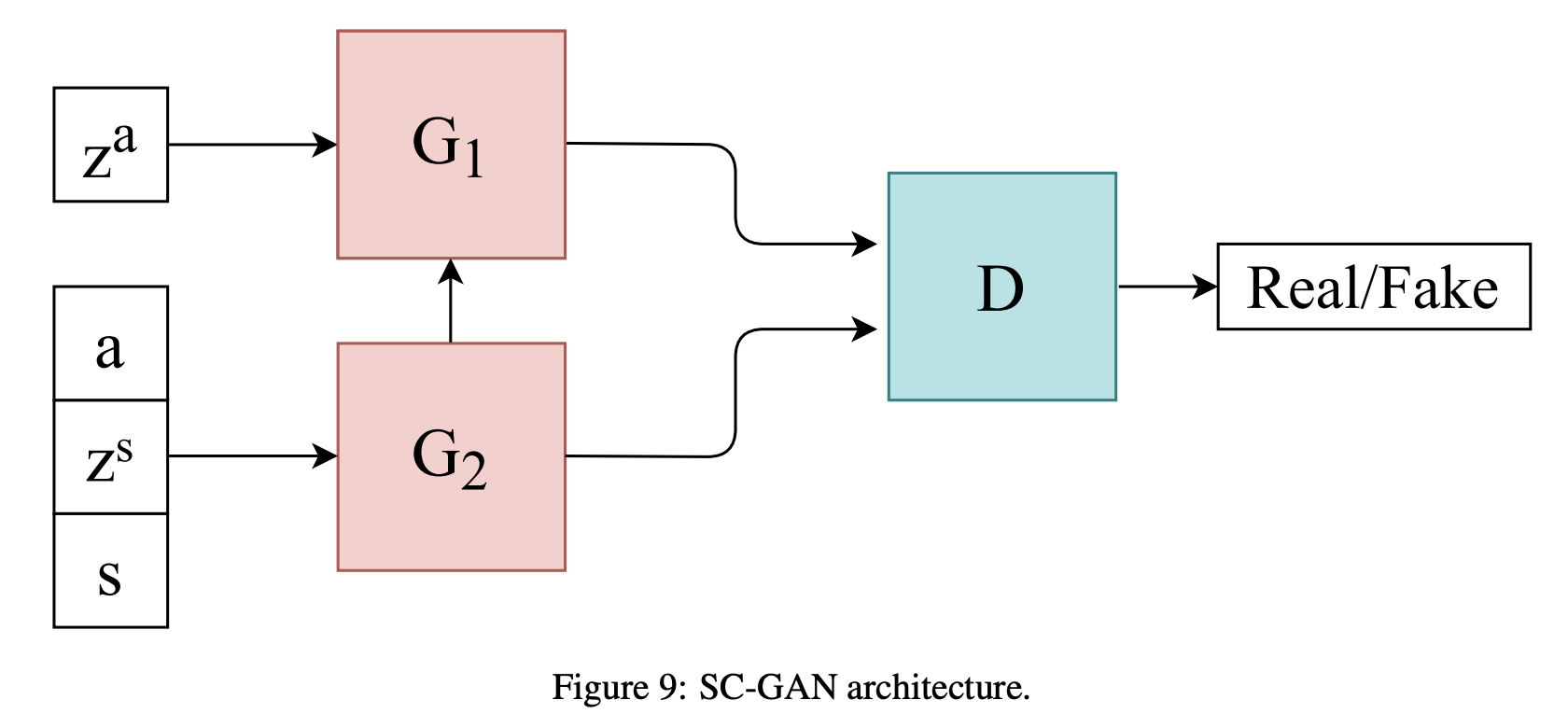
2019년 4월에 발표된 SC-GAN은 환자의 현재 상태와, 각 환자 상태에 맞는 권장 약물 복용량을 생성하기 위하여 제안되었음. 두 개의 coupled 된 generator가 각각 권장 복용량과 환자의 현재 상태를 생성함. Generator $G$는 두 개의 unidirectional LSTM으로 이루어져 있으며, Discriminator $D$는 두 개의 bidirectional LSTM으로 이루어져 있음.

$G_1$은 권장 약물 복용량을, $G_2$는 환자의 현재 상태를 생성하며 $D$는 입력된 sequential patient-centric record가 진짜 데이터인지 합성 데이터인지 구별함. SC-GAN은 MIMIC-III 데이터에서 훈련되었으며, 특정 use case에서는 SC-GAN이 SeqGAN, C-RNN-GAN, RCGAN 보다 나은 성능을 보여주었음.

Noise Reduction GAN (NR-GAN)

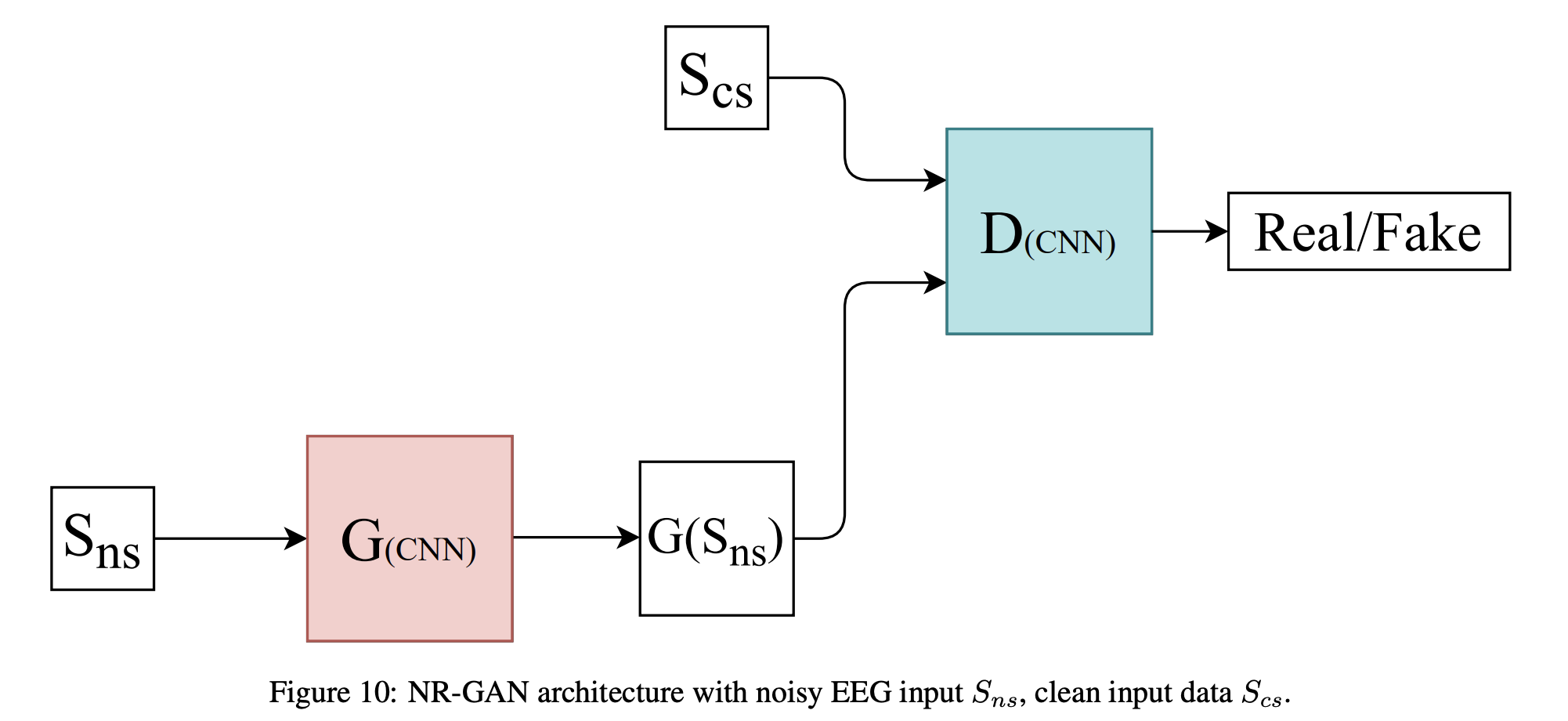
2019년 10월에 발표된 NR-GAN은 mice electroencephalogram(EEG) 신호에서의 noise reduction을 위하여 제안되었음. EEG 신호는 뇌의 전기적 활동을 측정하며, 많은 노이즈가 포함될 수 있음.

NR-GAN의 주요 아이디어는 EEG 신호의 frequency domain representationd에서 노이즈를 제거하는 것임. Generator $G$는 2개의 1D CNN layer와 fc layer로 구성되었으며, Discriminator $D$는 softmax 활성화 함수와 이어지는 2개의 1D CNN layer로 구성되어 있음.

각 네트워크의 손실 함수는 아래와 같음.

$S_{ns}$는 noise signal을, $S_{cs}$는 clear EEG signal을 의미함. $\alpha$는 noise reduction 강도를 조절하는 하이퍼파라미터임.

위의 손실 함수를 보면, $G$는 latent space($z$)에서 데이터를 생성하는 것이 아님을 확인할 수 있음($x \in S_{ns}$). $G$는 noise signal을 입력받은 후, clear signal을 생성하도록 훈련됨.

NR-GAN은 기존의 noise reduction filter와 경쟁력 있는 성능을 보여주었음. 하이퍼파라미터 $\alpha$ 조절 등의 문제가 있긴 하지만, NR-GAN은 GAN을 활용한 새로운 noise reduction 방법을 제안하였음.

TimeGAN

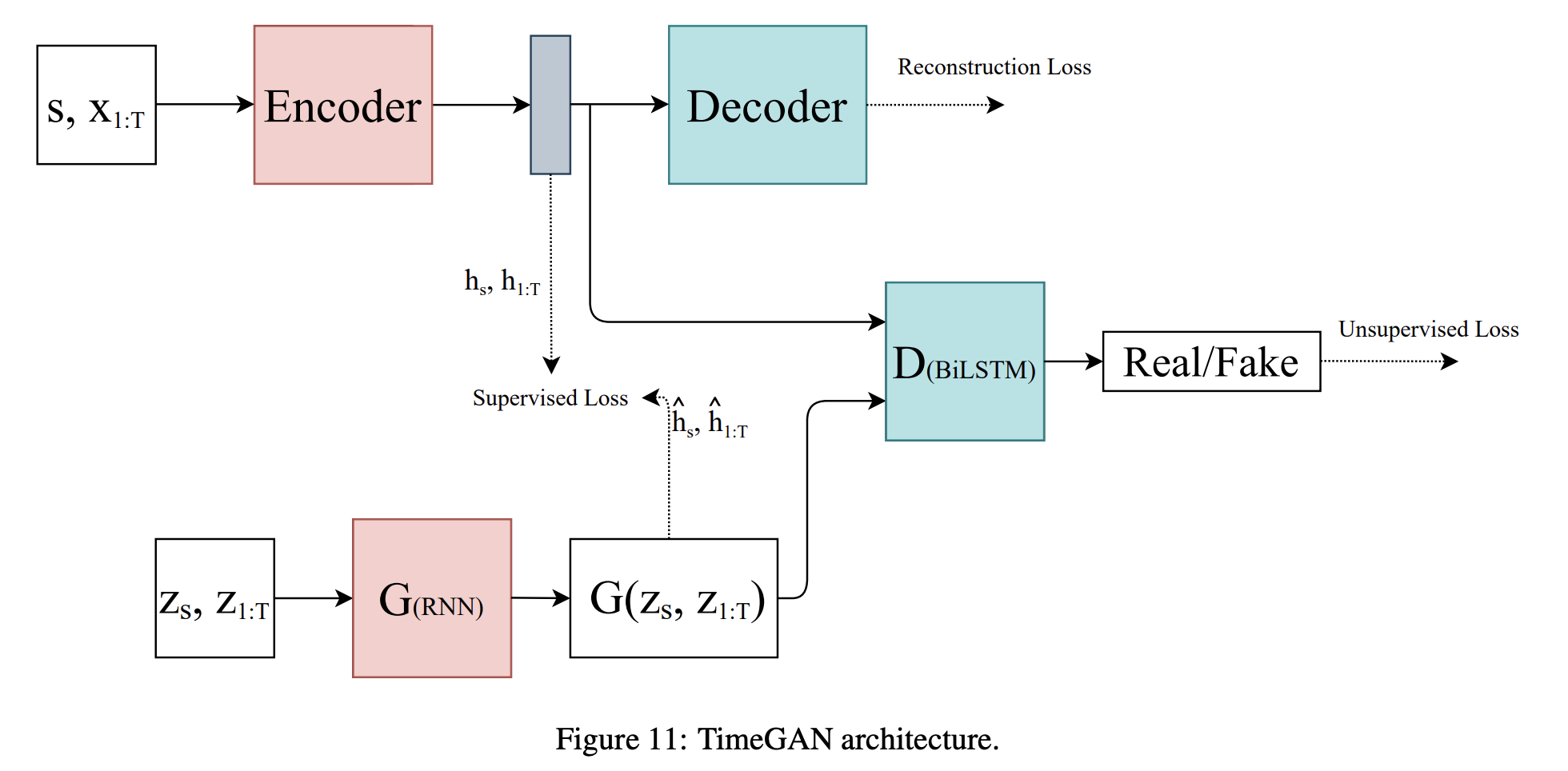
2019년 12월 발표된 TimeGAN은 conventional unsupervised GAN training method와 supervised learning approach를 동시에 사용하였음. Unsupervised GAN에 supervised autoregressive model을 추가함으로, 생성된 시계열 데이터는 원본 데이터의 temporal dynamics를 그대로 가지고 있음.

네트워크에 입력되는 $\mathbf{s}$는 static feature를, $\mathbf{x}$는 temporal feature를 의미함. Generator $G$는 실제 시계열 데이터를 생성하는 것이 아니라, latent code $h$를 생성함. $G$의 latent code와 encoder의 latent code를 사용하여 supervised loss를 계산하며, Discriminator $D$는 입력받은 latent code가 진짜인지 합성인지 구분함.

논문의 저자들은 generating sine wave 실험과 함께 stocks, energy, event dataset에서 TimeGAN의 성능을 확인하였으며, TimeGAN은 state-of-the-art (SOTA) 성능을 달성하였음.

Conditional Sig-Wasserstein GAN (SigCWGAN)

2020년 6월에 발표된 SigCWGAN은 lomg time series generation을 위하여 제안되었음.

이미지 생성에 있어, Wasserstein GAN(WGAN)은 discriminator network 대신 EM distance critic을 사용하였음. 해당 critic은 $p_g, p_r$ 분포 사이의 유사도를 계산함. WGAN은 $D$ network가 없으므로 generator / discriminator 사이의 균형을 조절할 필요가 없으며, 이러한 구조를 통해 mode collapse 문제를 해결하였음.

WGAN에서 EM distance critic을 사용한 것처럼, SigCWGAN은 생성된 데이터를 평가할 수 있는 새로운 지표 Signature Wasserstein-1 (Sig-W1)을 제안하였음. 해당 지표는 time series model의 temporal dependency를 포착하며, Wasserstein 지표처럼 높은 computation cost를 요구하지 않음.

또한 새로운 generator 구조, autoregressive feed-forward neural network(AR-FNN)를 제안하였음.

SigCWGAN은 S&P 500 index, Dow Jones index 등 다양한 현실 데이터셋과 합성 데이터셋에서 TimeGAN, RCGAN 등과 비교하여 state-of-the-art (SOTA) 성능을 달성하였음.

Decision Aware Time series conditional GAN (DAT-CGAN)

2020년 9월에 발표된 DAT-CGAN은 금융 포트폴리오 선택에서 최종 사용자의 의사 결정 프로세스를 지원하도록 설계되었음. Generator $G$는 decision-related quantities를 계산하는 데 사용되는 자산 수익률을 생성함.

해당 논문의 저자들은 DAT-CGAN이 최종 사용자의 의사결정 프로세스를 지원할 수 있는 높은 신뢰도의 시계열을 생성할 수 있다고 주장하였음. 다만, 모델의 계산 복잡도가 매우 크고 단일 생성 모델에 대해 1개월의 훈련 시간이 필요하다는 단점이 존재함.

Synthetic biomedical Signals GAN (SynSigGAN)

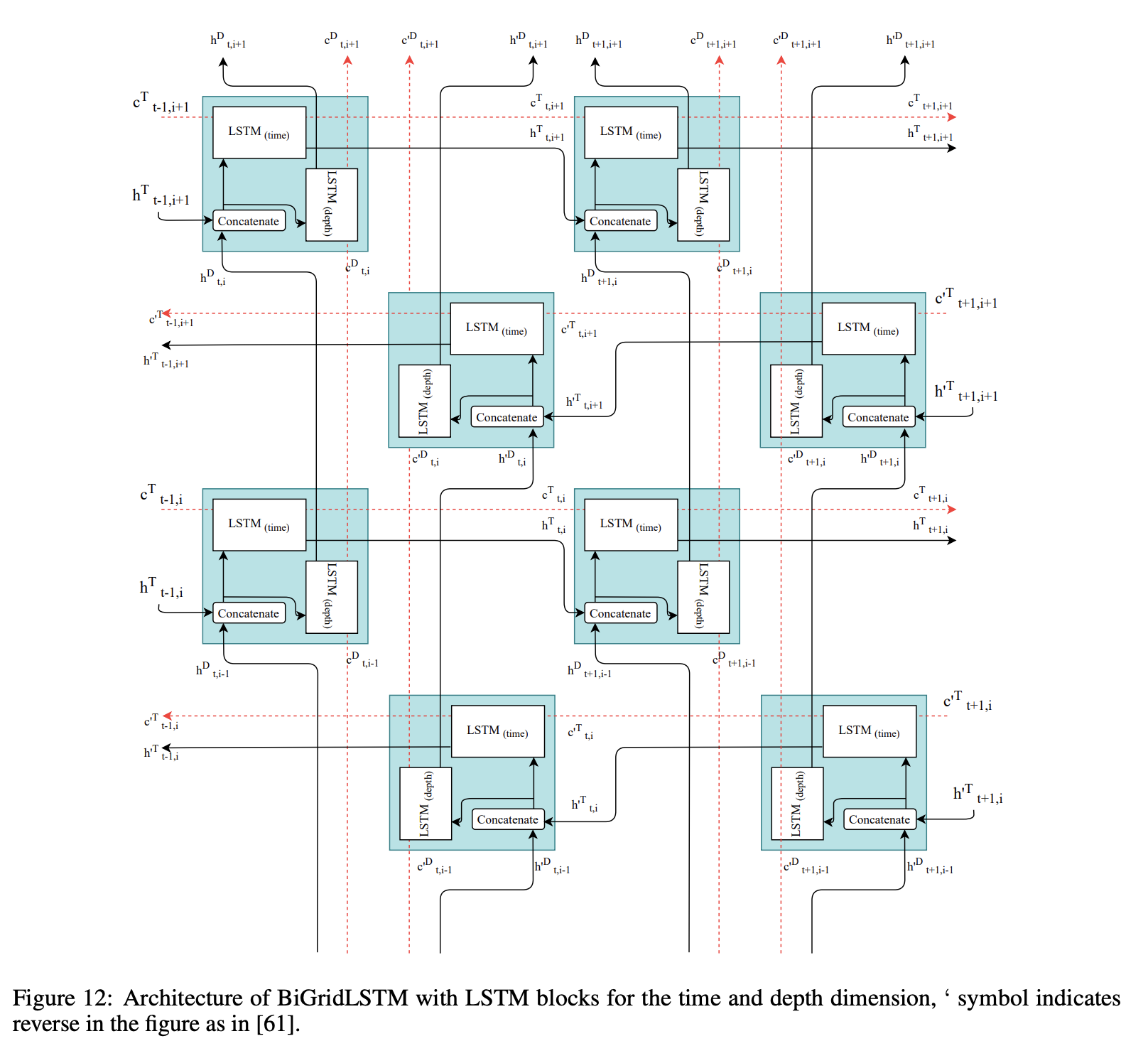
2020년 12월에 발표된 SynSigGAN은 다양한 종류의 연속적인 생리학 / 바이오메디컬 신호를 생성하기 위하여 제안되었음. SynSigGAN은 electrocardiogram (ECG), electroencephalogram (EEG), electromyography (EMG), photoplethysmography (PPG) 신호를 생성할 수 있음.

SynSigGAN은 bidirectional grid long short term memory (BiGridLSTM)를 사용하여 generator를 구현하였으며, CNN을 사용하여 discriminator를 구현하였음. BiGridLSTM은 GridLSTM의 조합으로, GridLSTM은 시공간 데이터를 모델링하기 위하여 horizontal 방향뿐만 아니라 vertical 방향으로도 정보(hidden state, cell state 등)가 전파되도록 개선된 아키텍처임.

SynSigGAN은 최대 191개의 데이터 포인트를 가지는 시계열 데이터를 생성할 수 있음.

5. Applications

이번 섹션에서는 time series GAN을 적용할 수 있는 상황에 대하여 알아봄.

5.1 Data Augmentation

데이터 부족(data shortage) 문제에 주로 사용되는 방법은 전이 학습(transfer learning)임. 전이 학습은 이미지 분류 등의 문제에서 많은 성과를 이루었음.

최근에는 GAN을 활용한 데이터 증강 기법을 사용하여, 전이 학습보다 더 나은 성능을 달성한 몇 가지 사례가 있음. 데이터의 양이 적고, 프라이버시 문제 등 접근이 어려운 private dataset의 경우 GAN을 사용한 데이터 증강이 기존의 전이 학습 방법보다 더 효과적일 수 있음.

의료 데이터와 같이 personal sensitive data와 관련된 연구를 진행하는 연구자들은 해당 데이터에 접근할 때 많은 어려움을 느낌. 이러한 데이터들은 소수의 연구자만 접근할 수 있고, 데이터와 데이터를 활용한 연구 결과 또한 자유롭게 공개할 수 없음. 이러한 문제는 해당 분야의 연구 발전 속도를 느리게 함.

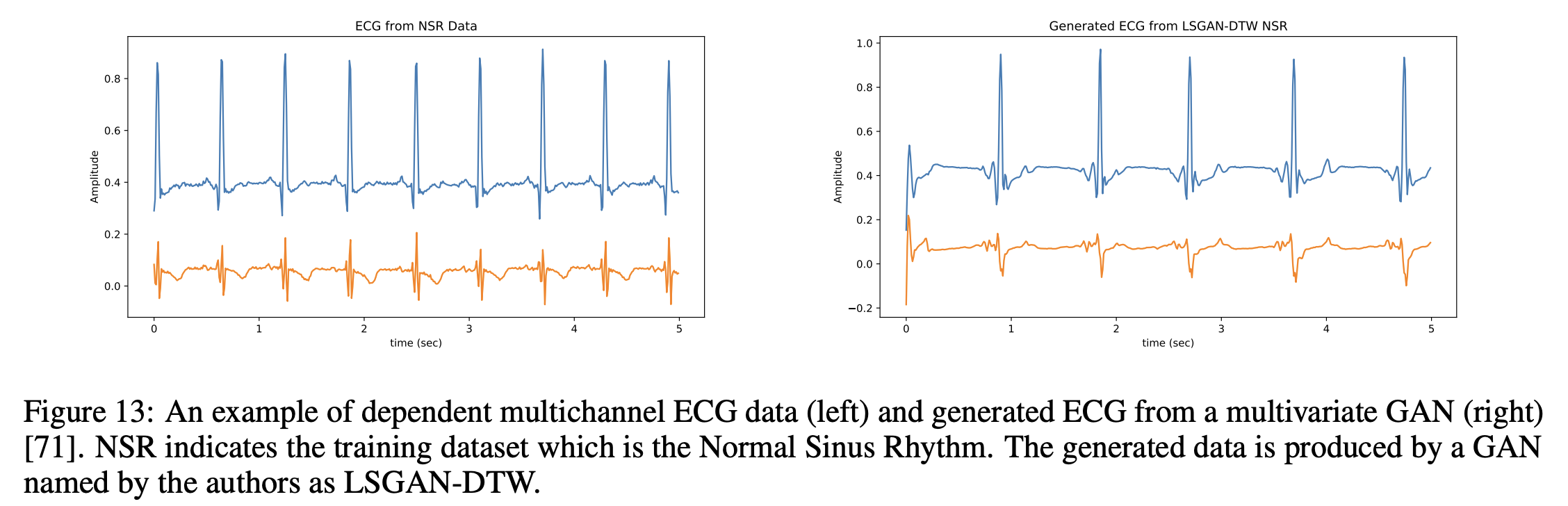
최근에는 GAN을 사용하여 의료 시계열 데이터를 생성하는 다양한 연구들이 진행되고 있음. 위의 Figure 13에서 생성된 예시를 확인할 수 있음.

의료 데이터뿐만 아니라, audio generation, text-to-speech(TTS), approximate / predict / forecast time series 등 GAN은 다양한 분야에 적용될 수 있음.

5.2 Imputation

현실 세계의 데이터는 쉽게 누락되거나 오염될 수 있음. 누락, 혹은 오염된 데이터를 다루는 전통적인 방법은 데이터 자체를 제거하거나, 평균 등의 통계량을 사용하거나, 머신러닝 기반의 방법을 사용하여 해당 값을 대체하는 것임.

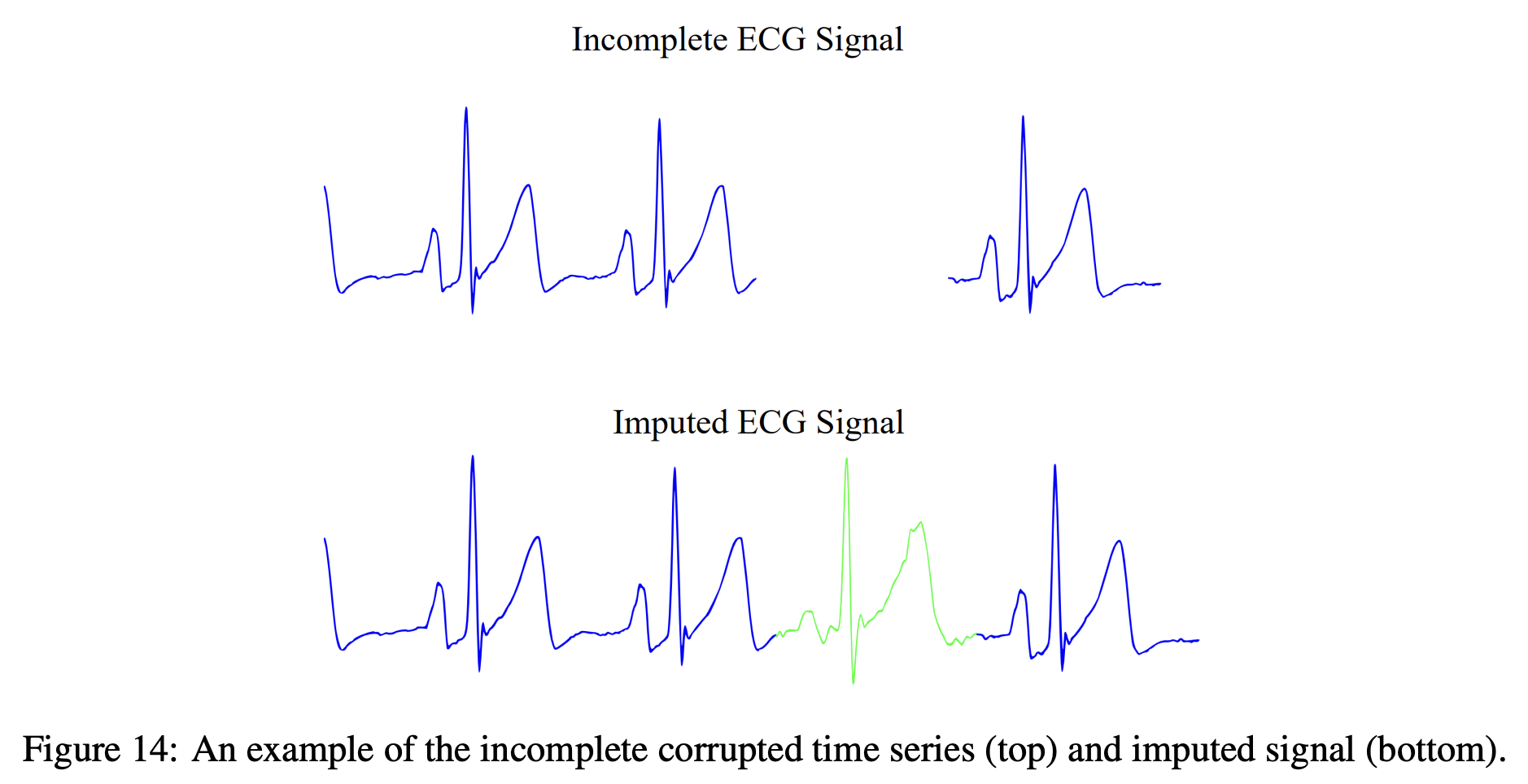
전통적인 방법뿐만 아니라, 위의 Figure 14와 같이 GAN을 사용하여 data imputation 작업을 수행할 수도 있음.

5.3 Denoising

시계열 데이터에는 자주 노이즈가 포함됨. 노이즈를 다루는 전통적인 방법은 adaptive linear filtering 과정을 수행하는 것임.

앞서 소개한 NR-GAN과 같이, GAN을 사용하여 시계열 데이터 내의 노이즈를 제거할 수도 있음. NR-GAN은 EEG 신호에서의 노이즈를 줄임.

5.4 Anomaly Detection

시계열 데이터에서 이상 탐지를 수행하는 것 또한 중요한 과제 중 하나임. 환자의 악성 상태 전조를 탐지하거나, 주식 시장의 비정상적인 트레이딩 패턴 등을 감지하는 것은 큰 도움이 될 수 있음.

통계량 기반의 이상 탐지 방법은 표면적으로는 잘 작동할 수 있으나, deeper feature에서는 중요한 이상치를 놓칠 수 있음. 또한, 기존의 통계 기반 방법은 large unlabelled dataset에서 좋은 성능을 얻지 못할 수 있음.

딥러닝 기반의 이상 탐지 기법은 large unlabelled dataset에서 기존의 방법보다 뛰어난 성능을 달성할 수 있고, GAN 기반의 이상 탐지 방법 또한 기존의 통계 기반 방법보다 더 나은 성능을 달성하였다는 연구 결과가 존재함. 이 외에도 GAN을 활용하여 심혈관 질환, 악의적인 플레이어, 주가 조작 등 비정상 샘플을 탐지한 연구 결과가 존재함.

5.5 Other Applications

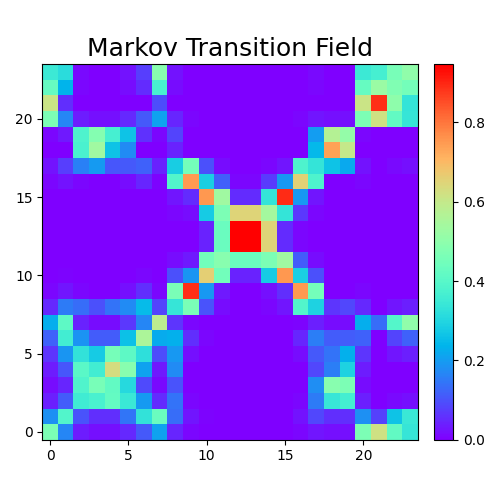
[이미지 출처]

위와 같이 시계열 데이터에 transformation function을 적용하여 이미지로 변환한 뒤, image-based GAN을 사용한 연구가 있음. GAN이 수렴되면, 훈련 데이터와 비슷한 이미지를 생성하고, 생성된 이미지에 inverse transformation을 적용하여 시계열 데이터를 얻음.

이러한 방법을 사용한 audio generation, anomaly detection, physiological time series generation 연구가 존재함.

6. Evaluation Metrics

앞서 언급하였듯 GAN의 성능을 평가하는 것은 어려우며, 어떤 평가 지표가 GAN의 성능을 가장 잘 표현하는지 아직까지도 합의된 것이 없음. 또한 지금까지 제안된 대다수의 평가 지표는 computer vision domain에 적합한 경우가 많음.

Time series GAN을 평가하는 지표는 크게 정성적 지표와 정량적 지표로 구분할 수 있음. 정성적 지표는 human visual assesment와 동일한 의미이며, 시계열 데이터의 특성상 객관적인 평가를 내리기 어려움.

정량적인 평가의 경우 대부분 통계량과 관련되어 있음. Correlation Coefficient (PCC), percent root mean square difference (PRD), (Root) Mean Squared Error MSE and RMSE, Mean Relative Error (MRE), Mean Absolute Error (MAE) 등의 지표가 흔하게 사용됨.

이미지 생성 GAN의 평가 지표인 Inception Score (IS), Fréchet (Inception) Distance (FD and FID), Structural Similarity Index (SSIM), maximum mean discrepancy (MMD), Sliced-Wasserstein Distance 등의 지표 또한 시계열 데이터 평가에 사용할 수 있음.

GAN을 사용하여 데이터를 생성한 다음 downstream classification task를 수행할 경우, Train on Synthetic, Test on Real (TSTR), 혹은 Train on Real, Test on Synthetic (TRTS) 평가 방법을 사용할 수도 있음. 이러한 방법은 downstream classifier의 precision, recall, F1 scores 등 다양한 성능을 확인하여 classifier의 학습 결과와 함께 생성된 데이터의 품질을 평가하는 방법임.

시계열 데이터에서 주로 사용되는 distance, similarity measures로는 Euclidean Distance (ED), Dynamic Time Warping (DTW) 알고리즘 등이 존재하며, 이 또한 생성된 시계열의 품질을 평가할 수도 있음.

이 외에도, 아래와 같이 다양한 분야의 평가 방법이 있음.

• Financial Sector: autocorrelation function (ACF) score, DY metric.
• Temperature Estimation: Nash-Sutcliffe model efficiency coefficient (NS), Willmott index of agreement (WI), Legates and McCabe index (LMI).
• Audio Generation: Normalised Source-to-Distortion Ratio (NSDR), Source-to Interference Ratio (SIR), Source-to-artifact ratio (SAR), t-SNE.

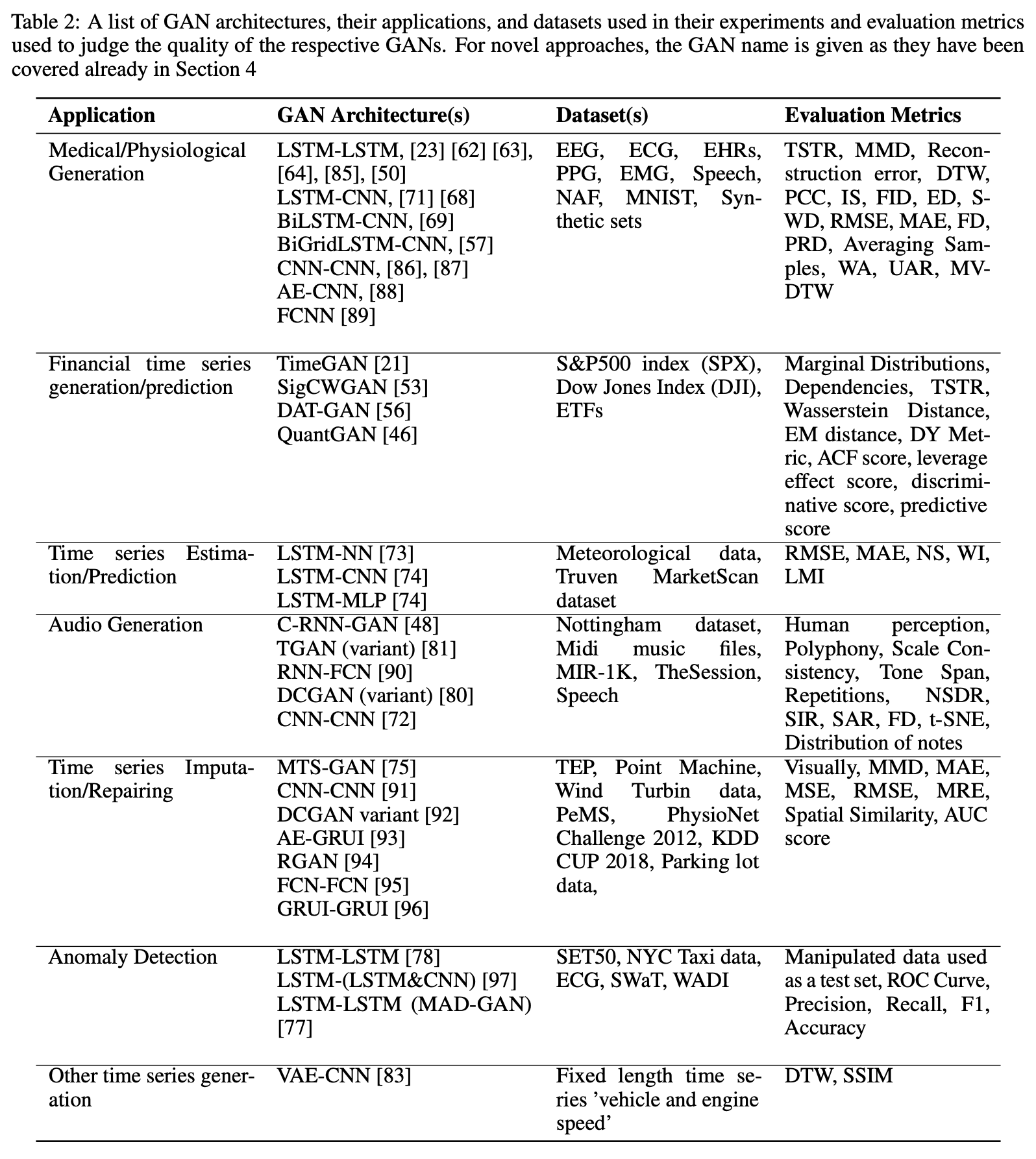
본 논문에서 소개된 다양한 GAN과 사용한 데이터셋, 평가 지표는 아래의 Table 2에서 확인할 수 있음.

7. Privacy

생성되는 데이터의 품질뿐만 아니라, 생성되는 데이터로 인해 발생할 수 있는 프라이버시 문제 또한 고려해야 함.

7.1 Differential Privacy

차등 정보 보호(Differential Privacy, DP)의 개념은 데이터베이스 A에서, 모든 자료가 존재했을 때의 데이터 분포와 어떤 자료 a를 제외했을 때의 데이터 분포가 동일하다면 정보 보호가 가능하다는 개념임. 예를 들어, 의료 데이터 분석을 진행할 때, 환자 a의 데이터가 포함되었는지 여부에 따라 분석 결과가 크게 달라지면 안 된다는 것임.

정보 보호를 위한 기존의 마스킹 방법 등은 다른 데이터와 결합할 경우 개인의 정보를 쉽게 추정할 수 있어, DP와 같이 정보 보호를 위한 새로운 개념 등이 제시되고 있음.

GAN의 경우, 생성된 데이터를 통해 특정 개인의 데이터가 GAN 훈련에 사용되었는지 여부를 알 수 없어야 DP를 달성할 수 있음. 즉, GAN의 생성 결과를 통해 원본 훈련 데이터의 개별 샘플을 추적 및 추정할 수 없어야 함.

DP와 같이 프라이버시를 보호할 수 있는 머신러닝 메커니즘이 많이 연구되고 있으며, 훈련 중 gradient에 noise를 더하여 DP를 달성한 differentially private GAN (DPGAN) 등 관련 연구가 존재함.

7.2 Decentralised / Federated Learning

기존의 머신러닝 & 딥러닝은 전체 훈련 데이터를 하나의 서버에 저장한 뒤 모델을 훈련하였음. Decentralised / Federated Learning은 전체 데이터를 하나로 모으지 않고, 각 환경에서 모델을 학습한 다음 모델 간 통신을 통하여 전체 모델을 학습시키는 방법론을 뜻함.

이러한 방법을 통해 이동이 어려운 민감한 데이터를 외부로 방출시키지 않을 수 있어, 프라이버시 관련 제약 조건을 지킬 수 있음. Federated learning GAN(FedGAN)과 같이 관련된 GAN 연구가 존재하나, FedGAN의 경우 differential privacy를 달성하였는지 실험하지 않고 향후 연구로 남겨두었음.

이러한 federated learning과 differential privacy를 결합한 새로운 GAN 알고리즘을 개발한다면, 개인 정보 유출 없이 데이터를 생성할 수 있는 완전히 분산된 개인 정보 보호 GAN(fully decentralised private GAN)으로 이어질 것임.

7.3 Assessment of Privacy Preservation

생성 모델이 프라이버시를 얼마나 보호하고 있는지 실험할 수도 있음. 대표적인 방법은 membership inference attack임. 해당 방법은 머신러닝 모델이 훈련에 사용된 개별 데이터 레코드에 대한 정보를 어느 정도 누출하는지 정량적으로 평가함.

허용 가능한 수준의 개인정보 보호를 위해서는 GAN이 생성하는 데이터의 품질을 희생해야 한다는 연구 결과가 존재하며, 반대로 DP 네트워크가 differential privacy를 준수하고 생성된 데이터의 품질 저하 없이 membership inference attack에 성공적으로 견딜 수 있는 데이터를 생성하였다는 연구 결과 또한 존재함.

8. Discussion

다양한 GAN 아키텍처와 목적 함수가 제안되었지만, 최고의 GAN은 아직 결정되지 않았음. GAN은 application-specific 한 경향이 있어 의도한 목적대로는 잘 동작하지만, 다른 도메인에서는 잘 일반화되지 않는 경우가 많음. 예를 들어, 고품질의 생리학적 시계열을 생성하는 GAN은 아키텍처 또는 손실 함수에 의해 부과된 제한으로 인해 고품질 오디오를 생성하지 못할 수 있음.

Time series GAN의 주요 한계점은 각 아키텍처마다 생성하고 잘 관리할 수 있는 sequenc의 길이가 모두 다르다는 것임. 다양한 time series GAN이 다양한 데이터 길이에 얼마나 잘 적응할 수 있는지에 대한 문서화된 실험 검증은 아직까지 존재하지 않음.

9. Conclusion

본 논문에서는 시계열 데이터에 적용할 수 있는 다양한 Generative Adversarial Networks에 대하여 알아보았음. 다양한 GAN 아키텍처와 함께, GAN을 적용할 수 있는 문제, 관련 데이터셋 및 각 도메인에 사용된 평가 지표 등을 소개하였음.

또한, time series GAN을 위한 평가 지표, differential privacy 및 federated learning 등 GAN과 관련된 다양한 open challenge를 소개하였음.

Appendix

Appendix에서는 3.2 Challenges에서 소개한 수학적 개념들을 보다 자세히 다룹니다.

KL Divergence

이 블로그의 포스팅을 참고하였습니다. 꼭 읽어보시기를 추천해 드립니다.

어떠한 이산 확률 분포 $p$가 있을 때, $p$의 Entropy $H(p)$는 다음과 같이 계산할 수 있습니다.

만약 $p$가 연속 확률 분포라면 $H(p) = \int p(x)\log_2 p(x)dx$ 등으로 계산할 수 있습니다. 엔트로피 $H$는 어떤 문제 $p$에 대한 최적의 전략하에 필요한 질문 개수(정보량)의 기댓값을 뜻합니다.

두 확률 분포 $p, q$가 있을 때, 두 분포 사이의 Cross Entropy $H(p, q)$는 다음의 식으로 계산할 수 있습니다.

Cross entropy는 어떤 문제($p$: 확률 분포)에 특정 전략($q$: 확률 분포)을 사용하였을 때, 예상되는 정보량의 기댓값입니다. 각 문제에 맞는 최적에 전략을 사용할 때, Cross entropy는 entropy와 동일하게 되어 최솟값을 가집니다.

$H(p, q)$을 다음과 같이 표현할 수 있습니다.

즉, $H(p, q)$는 $H(p)$에 어떠한 값이 더해진 것입니다. 이때 더해진 어떠간 값이 바로 KL divergence (쿨백-라이블러 발산) $D_{KL}$ 입니다.

KL divergence는 두 분포 $p, q$ 사이의 차이를 표현합니다. 값이 클수록 두 분포가 많이 차이 납니다. 위키백과의 정의는 다음과 같습니다.

"쿨백-라이블러 발산(Kullback–Leibler divergence, KLD)은 두 확률분포의 차이를 계산하는 데에 사용하는 함수로, 어떤 이상적인 분포에 대해, 그 분포를 근사하는 다른 분포를 사용해 샘플링을 한다면 발생할 수 있는 정보 엔트로피 차이를 계산한다 ... 쿨백-라이블러 발산은 어떠한 확률분포 $p$가 있을 때, 샘플링 과정에서 그 분포를 근사적으로 표현하는 확률분포 $q$를 $p$ 대신 사용할 경우 발생하는 엔트로피 변화를 의미한다."

$D_{KL}(p \Vert q)$는 아래와 같이 표현할 수 있습니다.

$D_{KL}(p \Vert q) = H(p, q) - H(p)$이고, $H(p, q)$의 lower bound가 $H(p)$이므로 $D_{KL}(p \Vert q) \ge 0$ 입니다.

또한, $D_{KL}(p \Vert q) \ne D_{KL}(q \Vert p)$ 입니다. 두 분포 $p, q$ 사이의 거리가 아닌 차이를 표현한다고 말한 것이 이 때문입니다. 거리를 표현한다면 $D_{KL}(p \Vert q) = D_{KL}(q \Vert p)$이 되어야 합니다.

KL divergence를 분포 간의 distance metric으로 사용할 수 있는 방법은 Jenson-Shannon Divergence $D_{JS}$를 사용하는 것입니다.

$D_{JS}$는 아래와 같습니다.

Global Optimity of GAN

생성 모델의 목표는 모델이 생성하는 데이터의 분포 $p_g$와 실제 데이터의 분포 $p_{data}$가 서로 유사해지는 것입니다.

두 분포가 유사하다는 것은 어떻게 계산할 수 있을까요? 한 가지 방법은 위에서 소개한 Jenson-Shannon divergence $D_{JS}(p_{data} \Vert p_g)$를 사용하는 것입니다. $D_{JS}(p_{data} \Vert p_g)$ 값이 작다는 것은 두 분포가 서로 유사하고, 생성 모델이 잘 학습되었다는 것을 의미합니다.

GAN은 아래의 목적 함수를 통해 최적화를 진행합니다.

$V(D,G)$를 최적화하는 것이 정말로 $p_{data}$와 $p_g$를 서로 유사하게 만들어줄까요? 즉, GAN의 최적해는 존재하는 것일까요? GAN의 저자는 아래의 수식을 통해 이를 증명하였습니다.

Discriminator
먼저, $D$ network를 먼저 훈련합니다. 따라서 위의 $\underset{G}{\text{min}} \, \underset{D}{\text{max}} \, V(G, D)$에서 $G$는 고정입니다.

식을 전개하면 다음과 같습니다. $D$를 훈련하므로, 아래의 식을 최대화해야 합니다.

$V(D, G)$를 최대화하는 것은 $p_{data}(x) \log D(x) + p_{g}(x) \log (1-D(x))$을 최대화하는 것과 동일합니다. 따라서, 찾고자 하는 최적의 $D^*$는 다음과 같습니다.

이때 $p_{data}(x)=a, p_g(x)=b, D(x)=y$로 치환하면 위의 식은 $a \log y + b \log (1-y)$가 되고, 이 식을 $y$에 대하여 미분하면 $\frac{a}{y} + \frac{-b}{1-y}$가 됩니다.

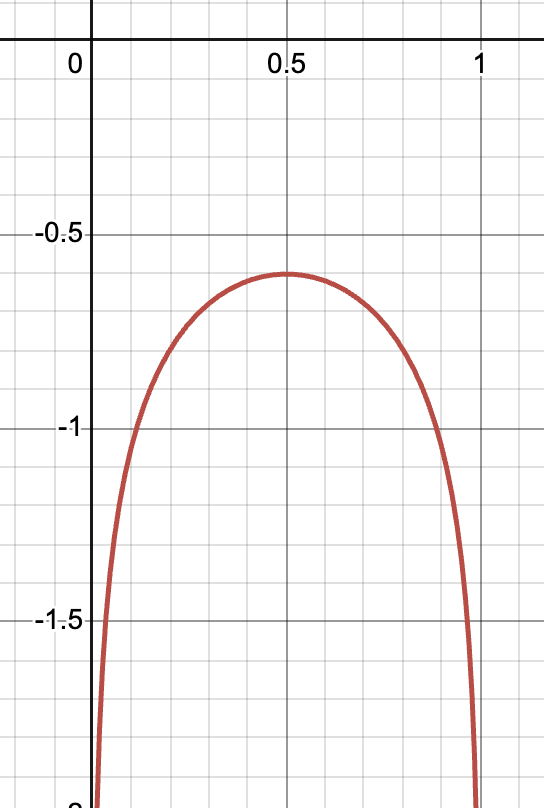
[ $\log x + \log (1-x)$의 그래프 개형 ]

미분한 식이 0이 되게 하는 $y$를 찾으면 $p_{data}(x) \log D(x) + p_{g}(x) \log (1-D(x))$이 최대가 되게 하는 $y=D(x)$를 찾을 수 있습니다. 몇 가지 간단한 연산을 통해, $y = \frac{a}{a+b}$ 일 때 최대라는 것을 알 수 있습니다.

즉, $D^*(x) = \frac{p_{data}(x)}{p_{data}(x) + p_g(x)}$ 일 때 $V(D,G)$를 최대화합니다.

Generator
$D$ 다음으로 $G$ network를 최적화합니다. $D$는 고정하고 $D^*$를 사용합니다. 즉, $\underset{G}{\text{min}} \, \underset{D}{\text{max}} \, V(G, D)$에서 $\underset{G}{\text{min}} \, V(G, D^*)$로 문제가 바뀌었습니다.

앞의 $-\log 4$는 상수이므로, $V(G, D^*)$를 최소화하는 것은 $D_{JS}(p_{data}(x) \Vert p_g(x))$를 최소화하는 것과 동일합니다. 즉, 두 데이터 분포 $p_g, p_{data}$가 서로 가까워집니다.

최적의 $G^*$는 $p_{data}(x) = p_g(x)$ 일 것입니다. 이때, $D^*(x) = \frac{p_{data}(x)}{p_{data}(x) + p_g(x)} = \frac12$가 됩니다.

Optimizing Reversed KL Divergence

앞서, gradient vanishing 문제를 해결하기 위하여 $G$에 대한 loss 식을 다음과 같이 변경하였습니다.

$G$에 대한 손실 함수를 개선함으로 vanishing gradients 문제를 어느 정도 보완할 수 있었지만, 식 (3)은 mode collapse 문제를 발생시킬 수도 있다고 하였습니다. 그리고 그 이유는, 식 (3)을 최적화하는 것이 reverse KL divergence $D_{KL}(p_g \Vert p_r)$을 최소화하는 것이기 때문이라고 언급하였습니다.

우선, 식 (3)이 왜 reverse KL divergence $D_{KL}(p_g \Vert p_r)$가 되는지 알아보겠습니다. $p_r$는 위에서 설명한 $p_{data}(x)$, 즉 실제 데이터 분포입니다.

마지막 식에 의해, $\mathcal L_G$는 다음과 같이 두 개의 식으로 분리됩니다.

이는 $\underset{G}{\text{min}} \, V(G, D^*) = \mathbb E_{x \sim p_{data}(x)}[\log D^*(x)] + \mathbb E_{x \sim p_g(x)}[\log (1 - D(x))]= -\log4 + 2 \times D_{JS}(p_{data} \Vert p_g)$ 이기 때문입니다. $p_r = p_{data}$ 입니다.

$\mathcal L_G$는 앞의 두 항에만 영향을 받습니다. $\log 4$는 상수이고 $\mathbb E_{x \sim p_r}[\log D^*(x)]$ 또한 $G$에 대한 식이 아니기 때문입니다. 또한, 전체 식은 $D_{KL}(p_g \Vert p_r)$에 의해 주로 영향을 받습니다. 이는 아래의 그림과 같이 $D_{JS}(p_r \Vert p_g)$의 값이 $[0, \ln2]$ 사이에만 존재하기 때문입니다. 이는 $D_{JS}(p_r \Vert p_g)$의 영향력이 전체 식에서 그리 크지 않다는 것을 의미합니다.

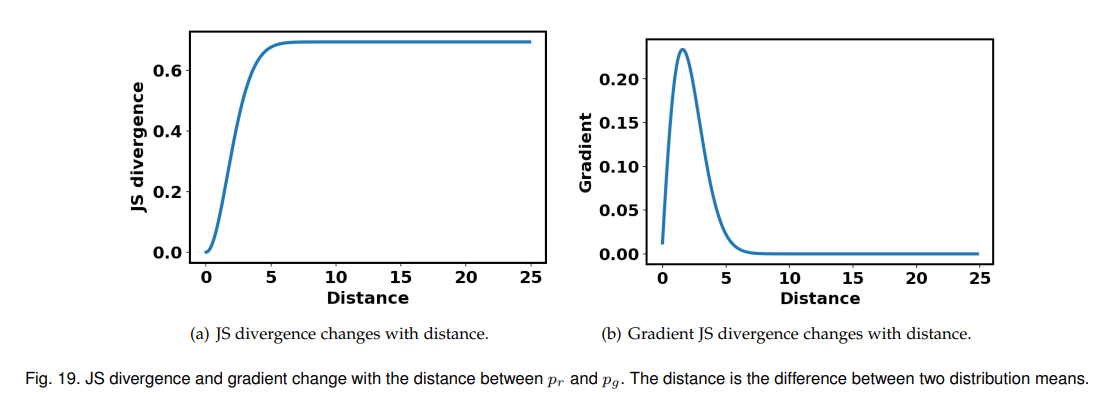
[출처 : Wang, Zhengwei, Qi She, and Tomas E. Ward. "Generative adversarial networks in computer vision: A survey and taxonomy." ACM Computing Surveys (CSUR) 54.2 (2021): 1-38.]

위의 식을 통해, $\mathcal{L}_G$를 줄이는 것은 결국 $D_{KL}(p_g \Vert p_r)$을 줄이는 것과 거의 동일한 것임을 알았습니다. $D_{KL}(p_g \Vert p_r)$에서, $p_r$과 $p_g$의 위치가 반대가 되었기 때문에 이를 reverse KL divergence라고 합니다. 보통은 실제 분포 $p_r$이 왼쪽에 적혀 있습니다.

그렇다면, reverse KL divergence $D_{KL}(p_g \Vert p_r)$을 최적화하는 것이 왜 아래 이미지의 오른쪽과 같은 mode collapse를 발생시킬 수 있을까요?

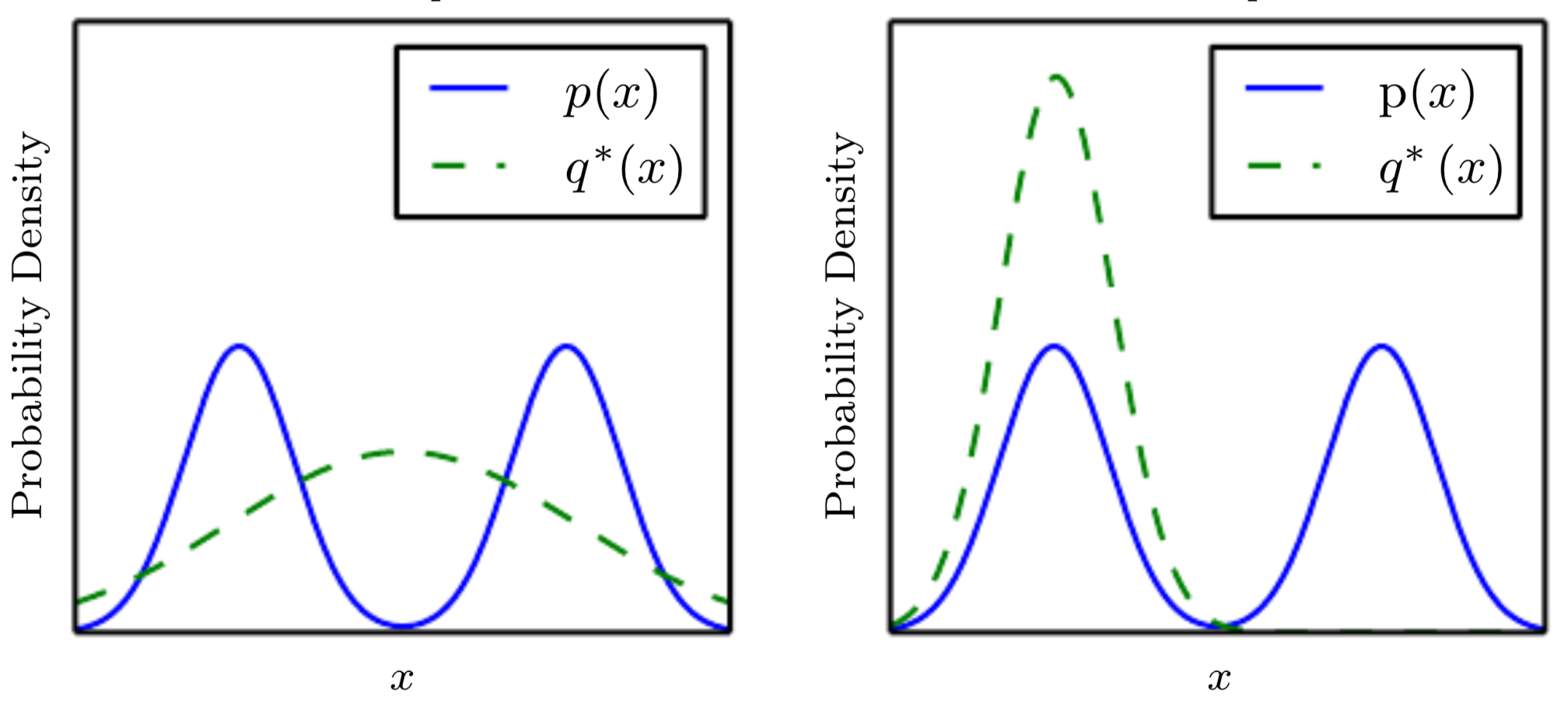
위의 그래프에서 $p(x)$를 $p_r$, 즉 이미 고정된 데이터의 실제 분포라 생각하고, $q^*(x)$를 생성 모델이 생성하는 데이터 분포 $p_g$라고 생각하겠습니다. $p(x)$는 고정되었지만 $q^*(x)$는 모델 학습 결과에 따라 얼마든지 달라질 수 있습니다.

이제, $D_{KL}(p_g \Vert p_r)$을 최소화하겠습니다. 간단히 $p, q$로 적겠습니다. $\theta$는 $q$의 파라미터입니다.

$\mathbb E_{x \sim q_\theta}[\log p(x)]$ 부분을 보면, $q$에서 나타나는 $x$에 대해, $p(x)$ 값이 커지도록 유도합니다. $H(q_\theta)$ 부분은 $q$ 분포의 엔트로피를 증가시켜 분산이 큰 분포를 유도합니다.

만약 위 그림의 왼쪽 그래프와 같이, $q$에서 나타나는 $x$가 전 영역을 커버한다면 어떻게 될까요? $p(x)$의 그래프 형태상, 중간에 위치하는 $x$에 대한 $p(x)$ 값은 매우 작아질 것입니다.

반대로 위 그림의 오른쪽 그래프와 같이, $q^*(x)$가 $p(x)$의 하나의 mode로 수렴되면 어떻게 될까요? $x$에 대한 $p(x)$ 값은 매우 커질 것입니다. 즉, $\mathbb E_{x \sim q_\theta}[\log p(x)]$ 부분 때문에 $q$ 분포가 $p$ 분포의 하나의 mode로 수렴되어 mode collapse 문제가 발생하는 것입니다.