---

본 포스팅은 제가 읽었던 논문을 간단하게 정리하는 글입니다. 논문의 모든 내용을 작성하는 것이 아닌, 일부분만 담겨 있으므로 자세한 내용은 원본 논문을 확인해 주시기를 바랍니다. 또한, 논문을 잘못 이해한 부분이 있을 수 있으므로, 양해 바랍니다.

Overview

Image segmentation을 위한 foundation model Segment Anything (SAM)은 2D natural image에서는 많은 성과를 이루었지만, CT, MRI와 같은 3D medical image에 SAM을 적용하기에는 아직 어려운 점이 남아 있음.

어려운 점 중 하나는 SAM이 훈련된 2D natural image와 3D medical image 사이에 많은 차이가 있다는 것임. 이러한 차이를 극복할 수 있는 추가적인 모델 설계가 필요함. 이 외에도, SAM의 특성상 생성되는 mask의 클래스를 예측하지 못한다는 것, box 또는 point 등 적절한 input prompt가 필요하다는 것 등 다양한 문제가 존재함.

본 논문에서는 3D medical image segmentation을 수행할 수 있는 prompt-free SAM architecture인 MaskSAM를 제안함. 아래의 Fig. 1과 같이 Prompt Generator라는 새로운 구조를 추가하여, 이미지 입력 시 자동으로 $N$개의 binary(auxiliary) mask, box, classifier token을 생성함. Binary mask와 box는 이후 mask decoder의 prompt로 사용되며, classifier token은 생성된 mask의 class 예측을 위해 사용됨.

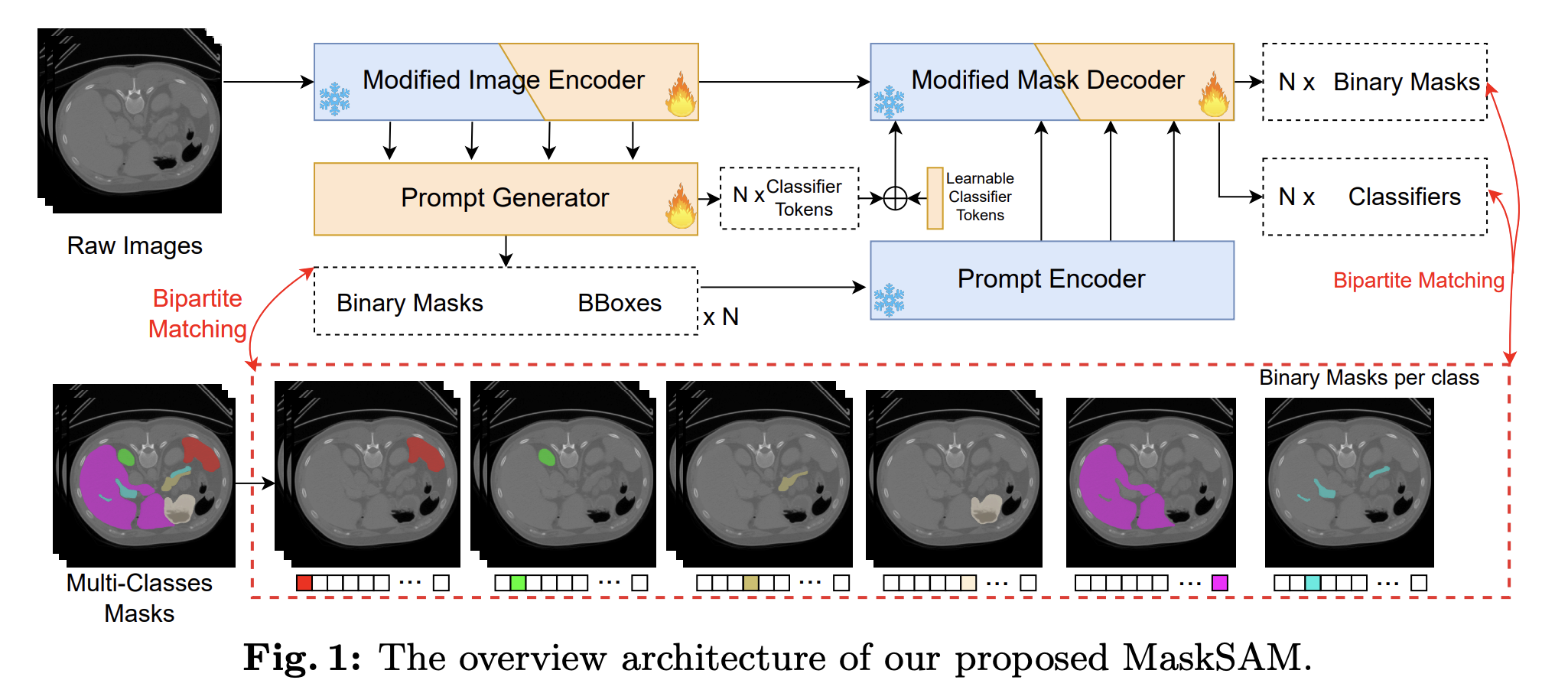
모델 학습을 위해, 주어진 multi-class segmentation dataset의 각 이미지를 Fig. 1의 하단 부분처럼 여러 개의 GT binary mask로 분할하였음.

각 class에 대한 one-hot encoding 처리로 이해하시면 됩니다.

Prompt Generator는 $N$개의 mask 등을 생성하며, $N$은 한 이미지 내에서 등장할 수 있는 최대 class의 개수보다 큰 값임.

객체 탐지 모델인 DETR에서와 같이, 생성된 $N$개의 mask와 set of GT binary mask 사이의 bipartite matching을 찾은 후, 최적의 permutation에 대한 loss를 기준으로 모델을 학습시킴. 자세한 것은 아래 내용 참고.

또한, 아래와 같이 SAM 내부 구조에 깊이 정보를 고려할 수 있는 lightweight adapter를 추가하여 효율적인 fine-tuning 작업(PEFT)을 수행할 수 있도록 하였음.

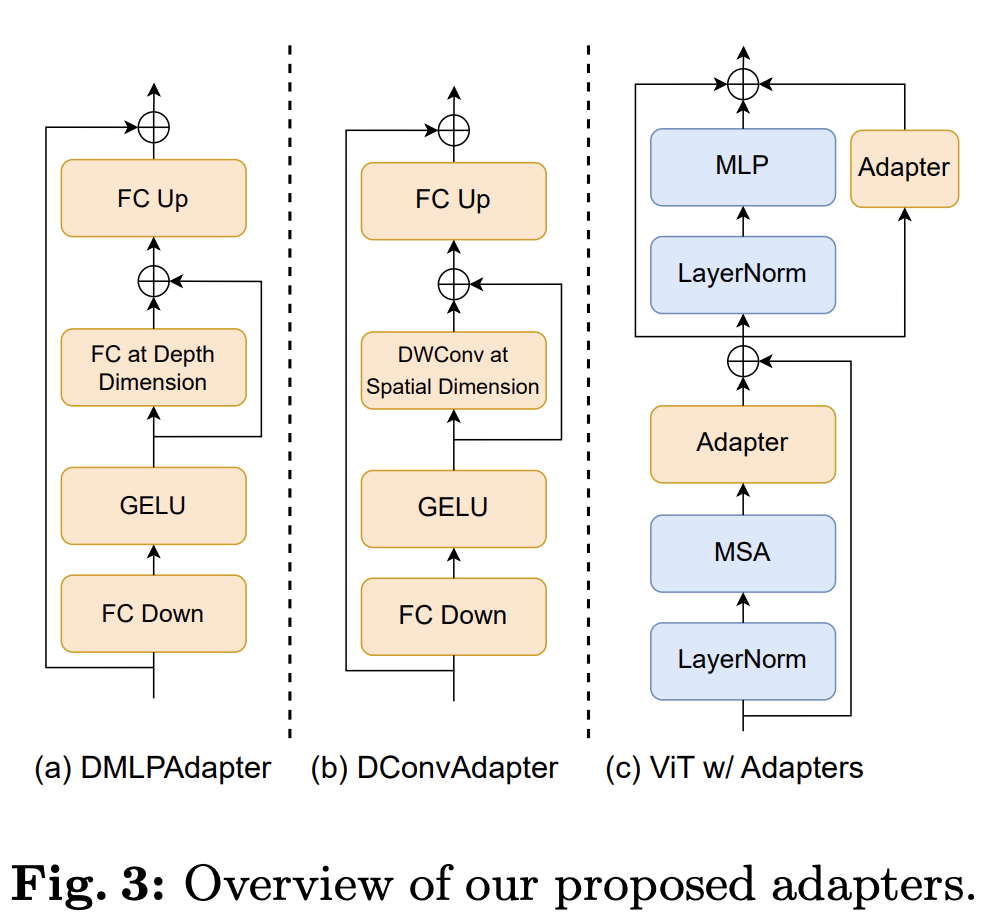
기존의 SAM 파라미터는 추가로 학습하지 않고, 새로 추가되는 구조(prompt generator, adapter 등)만 학습하여 효율적인 학습을 진행하였음. Adapter 구조는 image encoder와 mask decoder에 추가됨.

공식 코드 구현이 공개되어 있지 않아 부정확한 정보가 있을 수 있습니다.

Background

이번 섹션에서는 모델 학습의 핵심 단계인 bipartite matching에 대해 간단히 알아봄.

DETR 논문 리뷰를 다룬 블로그 포스팅을 참고하여 작성합니다.

Bipartite Matching

Bipartite matching은 두 집합 사이의 일대일 대응 시 가장 비용이 적게 드는 매칭을 의미함. 여기서 비용은, 우리가 흔히 아는 loss 등으로 이해할 수 있음.

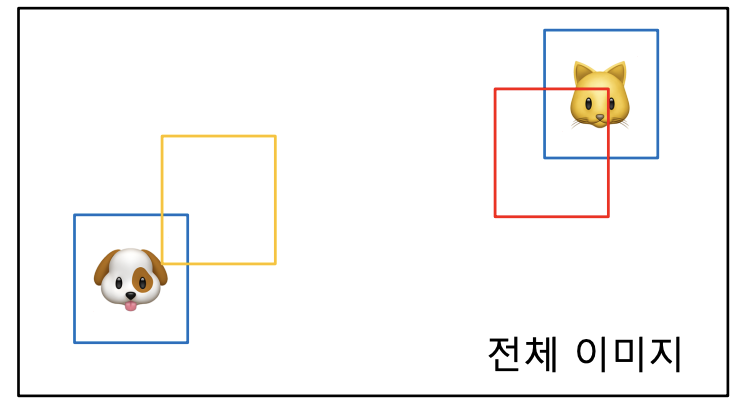
위와 같이 이미지에 2개의 객체(강아지, 고양이)가 있고, 2개의 bbox(빨강, 노랑)가 생성(예측)되었다고 하면, 아래와 같이 2개의 매칭이 생성될 수 있음.

• {(빨간색, 고양이), (노란색, 강아지)}
• {(빨간색, 강아지), (노란색, 고양이)}

고려하는 비용(loss)이 IoU loss($1 - \text{IoU}$)라면, {(빨간색, 고양이), (노란색, 강아지)} 매칭에 더 적은 비용이 필요함. 즉, 해당 매칭이 바로 bipartite matching임.

실제로는 이미지 내 더 많은 객체가 있을 수 있고, 더 많은 개수($N$)의 bbox가 생성되므로 hungarian algorithm을 사용하여 bipartite matching을 찾음. Hungarian algorithm에 대한 자세한 설명은 생략함.

아래의 예시는 이미지 내에 2개의 객체가 있고, 5개의 bbox를 예측한 경우임.

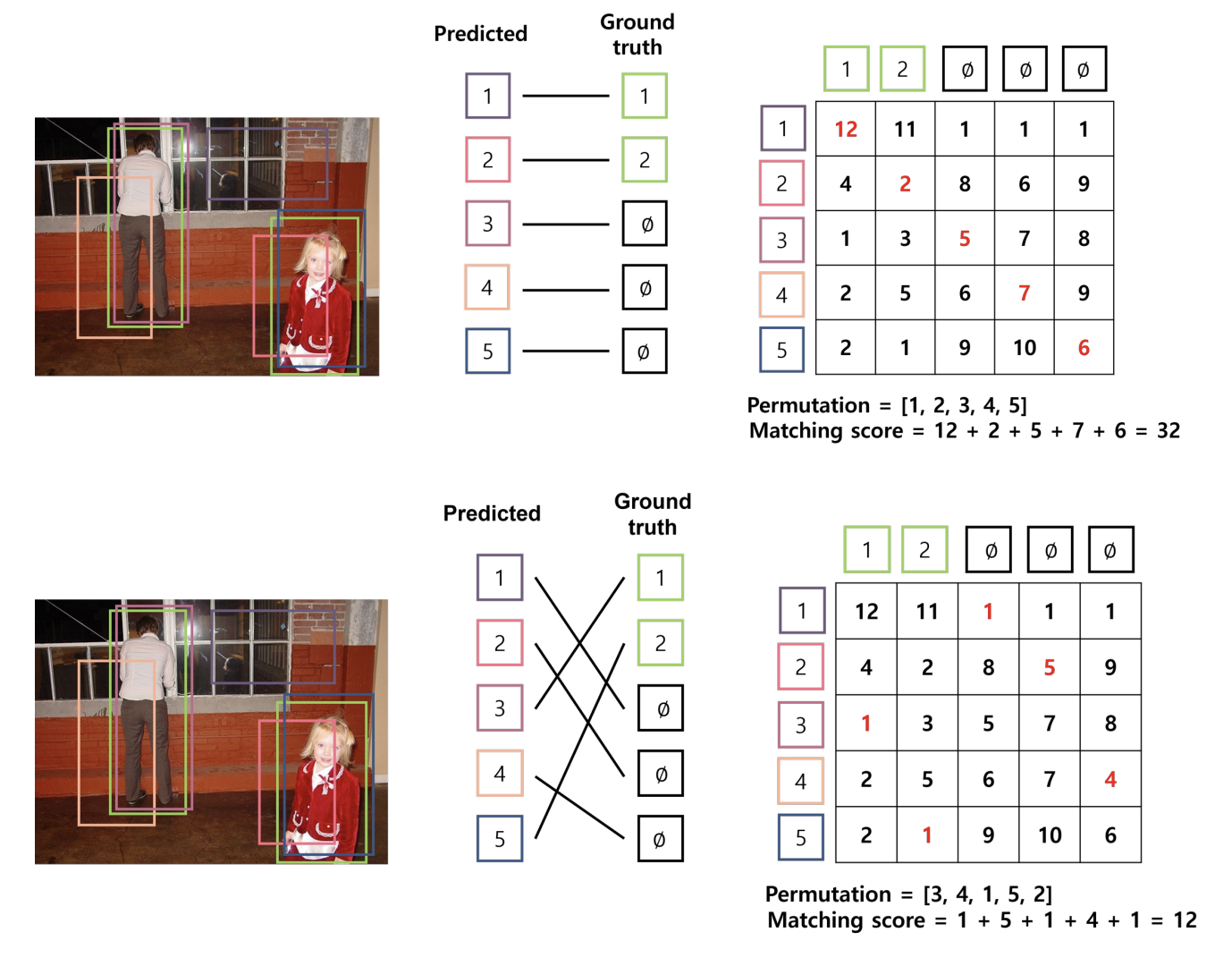
[이미지 출처]

생성된 5개의 bbox 중 GT bbox와 비용이 가장 적게 드는 2개의 bbox를 찾아 매칭하고, 나머지 3개의 bbox는 $\varnothing$(no object)와 매칭함. 예측 bbox와 GT bbox 사이의 매칭 결과에 따라 matching score(cost)가 달라지는 것을 볼 수 있음.

이와 같이, 모델 학습 과정에서 matching score를 최소로 하는 permutation $\sigma$를 찾고, 해당 매칭에 대한 loss를 계산하여 파라미터를 업데이트함.

Cost Matrix

위의 예시에서는 단순히 IoU loss만을 비용으로 사용하였지만, 다양한 요소를 조합하여 matching에 대한 비용을 계산할 수 있음.

DETR에서는 다음의 수식으로 비용을 정의함. $c_i$와 $b_i$는 GT class label과 bbox를 의미함.

$\hat p_{\sigma(i)}(c_i)$는 예측 결과에 대한 class probability를 의미하고, $\hat b_{\sigma(i)}$는 예측 bbox를 의미함.

$\mathcal L_{box}$는 아래의 수식으로 계산됨.

$\mathcal L_{iou}$는 GIoU loss를 의미함.

즉, $\mathcal L_{match}$는 생성된 예측의 올바른 클래스 확률이 높을수록, 생성된 bbox와 GT bbox 사이의 거리가 가깝고(L1 loss) 많이 겹칠수록(GIoU loss) 작아짐. 아래의 그림으로 간단한 예시를 확인할 수 있음. 클래스 확률은 임의로 설정하였음.

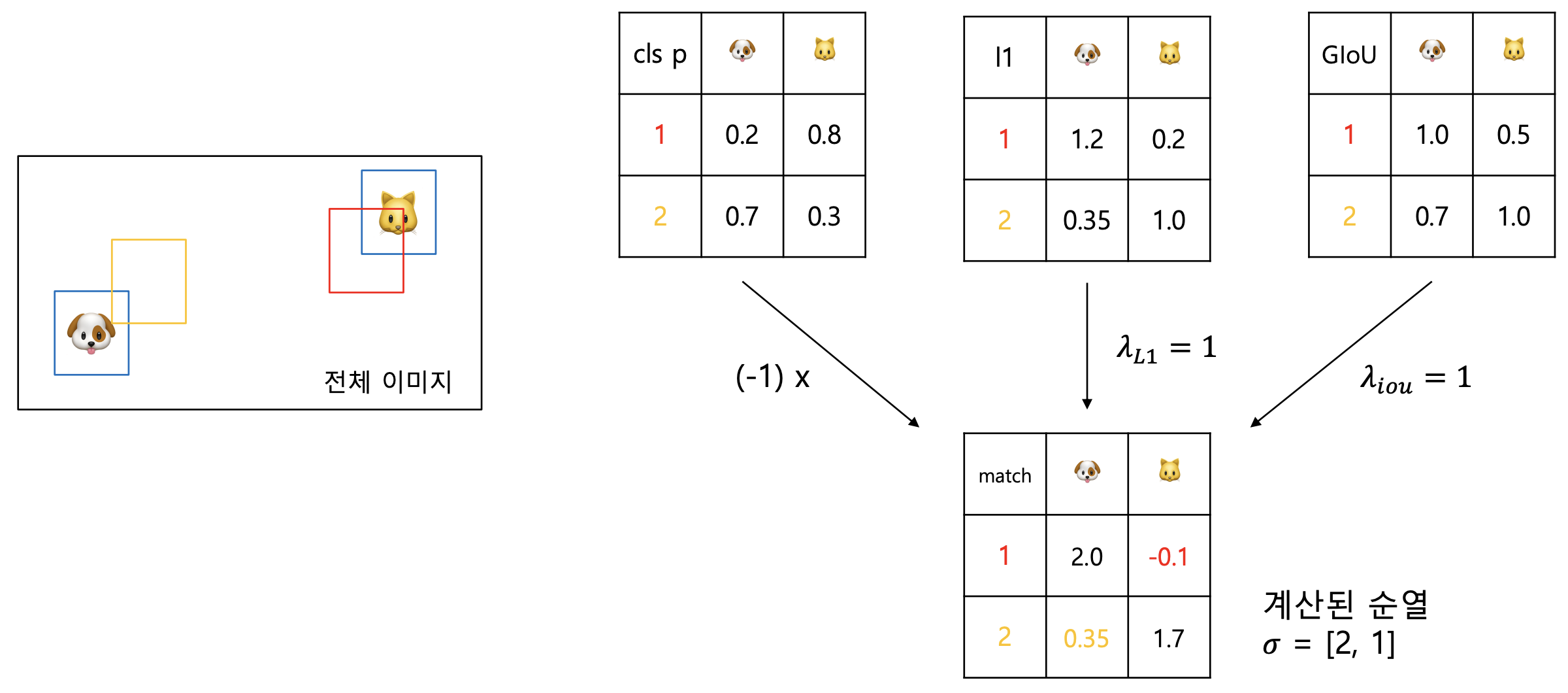
Loss & Update

Hungarian algorithm을 통해 최적의 permutation $\hat \sigma$를 찾으면, 해당 permutation을 기반으로 모델 학습을 위한 hungarian loss를 계산함.

위의 수식에서와 같이 클래스 확률에 대한 negative log-likelihood loss와 앞서 사용한 box loss를 사용함. 실제로는 $c_i = \varnothing$인 경우가 훨씬 많으므로, $c_i = \varnothing$에 대한 log probability를 1/10로 줄여 불균형 문제를 완화함.

DETR은 위의 과정을 따라 학습을 진행함. MaskSAM의 경우 $N$개의 binary mask와 bbox가 생성되는데, 생성된 mask & bbox에 대한 최소 비용을 가지는 permutation $\hat \sigma$을 찾은 후 loss를 계산하여 학습을 진행함.

Method

아래의 Fig. 4를 통해 MaskSAM의 전체 아키텍처를 확인할 수 있음.

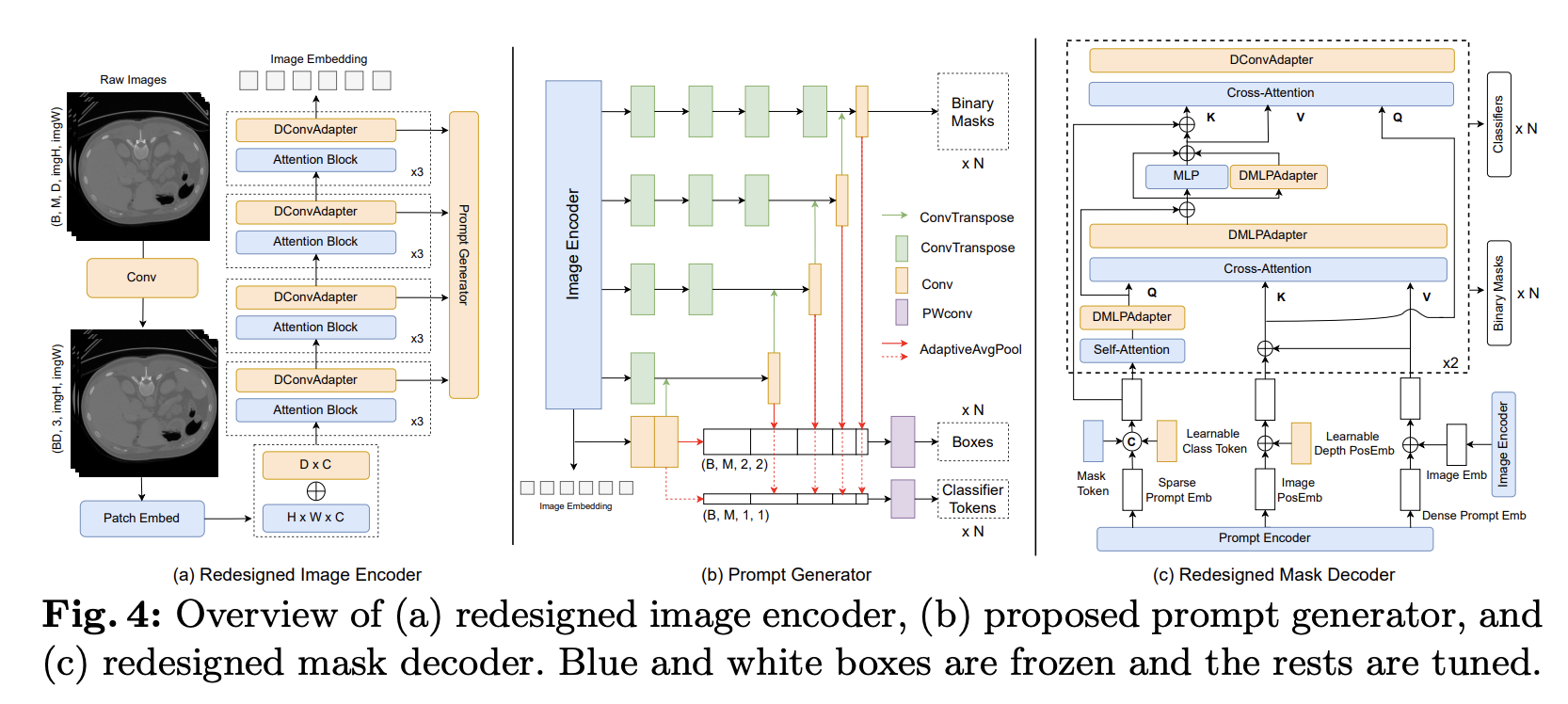
Proposed Prompt Generator

Fig. 4의 (b)에서 본 논문에서 제안하는 prompt generator를 확인할 수 있음.

Image encoder(vit-b)의 3, 6, 9, 12번째 transformer block 출력 feature map과 최종 출력을 prompt generator에 입력하여 $N$개의 binary mask, box, classifier token을 생성함.

생성되는 최종 mask는 입력 이미지와 동일한 크기를 가지며, $N$개의 채널을 가짐. 즉, 하나의 채널이 하나의 binary mask를 의미함. Transformer block 출력 텐서의 크기(e.g., ($B, 64, 64, \text{embed\_dim}$))를 원본 이미지의 크기만큼 늘리기 위하여 여러 번의 ConvTranspose 연산을 수행함.

각 feature map은 마지막 ConvTranpose 이후 Conv layer를 지나 lower level의 feature map과 이어짐(concatenate). Conv layer를 지난 feature map에 adaptive average pooling layer를 적용하여 고정된 크기((2, 2) & (1, 1))의 feature map을 생성하고, 이를 통해 $N$개 mask에 대한 box 좌표(x, y, w, h)와 classifier token을 계산함.

Prompt generator를 통해 아래와 같은 auxiliary prompt를 생성할 수 있음.

본 논문에서는 (d) 방법을 사용하여 실험을 진행하였음.

Modified Image Encoder

Fig. 4의 (a)에서 본 논문에서 제안하는 modified image encoder를 확인할 수 있음.

본 논문에서 새로 제안하는 DConvAdapter와 함께, 3D medical image의 깊이 차원을 고려하는 learnable depth positional embedding 등이 추가되었음.

Modified Mask Decoder

Fig. 4의 (c)에서 본 논문에서 제안하는 modified mask decoder를 확인할 수 있음.

Prompt generator에서 생성된 mask & box & classifier token을 image embedding과 함께 입력받아 최종 $N$개의 mask를 생성함. 생성된 classifier token 정보를 활용하여, 각 mask의 semantic label을 예측하도록 구현됨.

이 외에도, 본 논문에서 새로 제안하는 DMLPAdapter, DConvAdapter 등이 추가되었음. 모델 구조에 대한 자세한 설명은 원본 논문을 참고.

Losses and Matching

MaskSAM은 $N$개의 auxiliary mask, box, classfier token과 함께 $N$개의 최종 binary mask, mask class prediction 결과를 생성함. 앞서 설명한 DETR의 학습 과정과 유사하게, 생성된 $N$개의 예측 집합과 GT 집합 사이의 bipartite matching $\hat \sigma$을 찾아 학습을 진행함.

Cost matrix를 계산하기 위해 아래의 세 loss를 고려함.

• $\mathcal L_{mask}^{aux}$ : auxiliary mask prediction에 대한 binary cross-entropy loss와 dice loss
• $\mathcal L_{box}$ : auxiliary bbox에 대한 L1 loss와 GIoU loss
• $\mathcal L_{mask}^{final}$ : final mask prediction에 대한 binary cross-entropy loss와 dice loss + mask class prediction에 대한 cross-entropy loss

위의 수식을 통해 각 매칭에 대한 cost를 계산하고, hungarian algorithm을 사용하여 최적의 매칭 $\hat \sigma$을 찾은 후 모델 학습을 위한 loss를 계산함.

모델 학습을 위한 loss는 아래와 같이 계산됨.

Experiments

공개된 3개의 데이터셋, AMOS22 Abdominal CT Organ Segmentation, Synapse multiorgan segmentation, Automatic Cardiac Diagnosis Challenge(ACDC)에서 실험을 수행하였음.

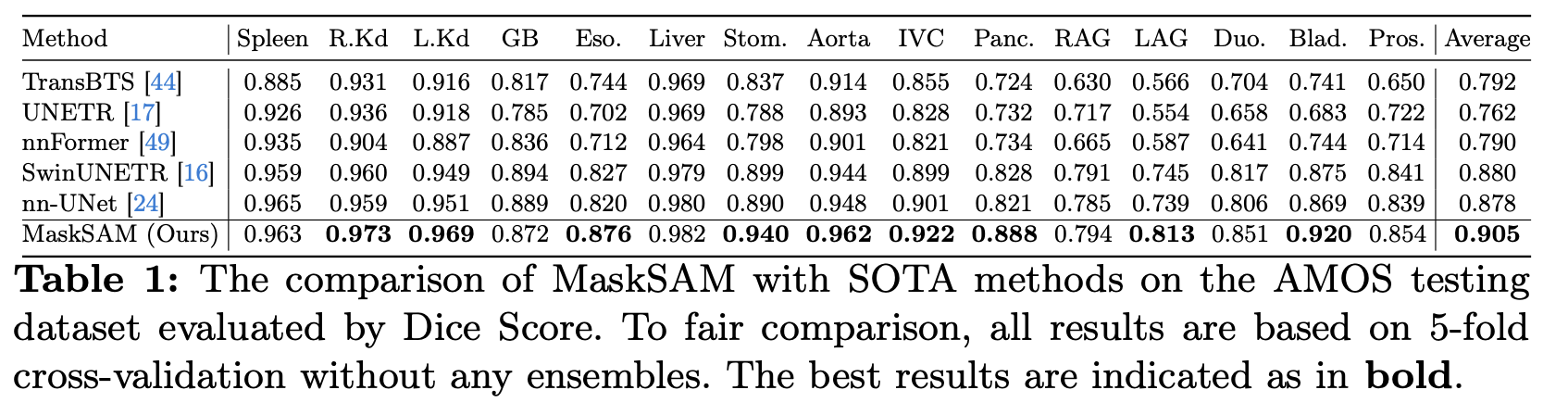
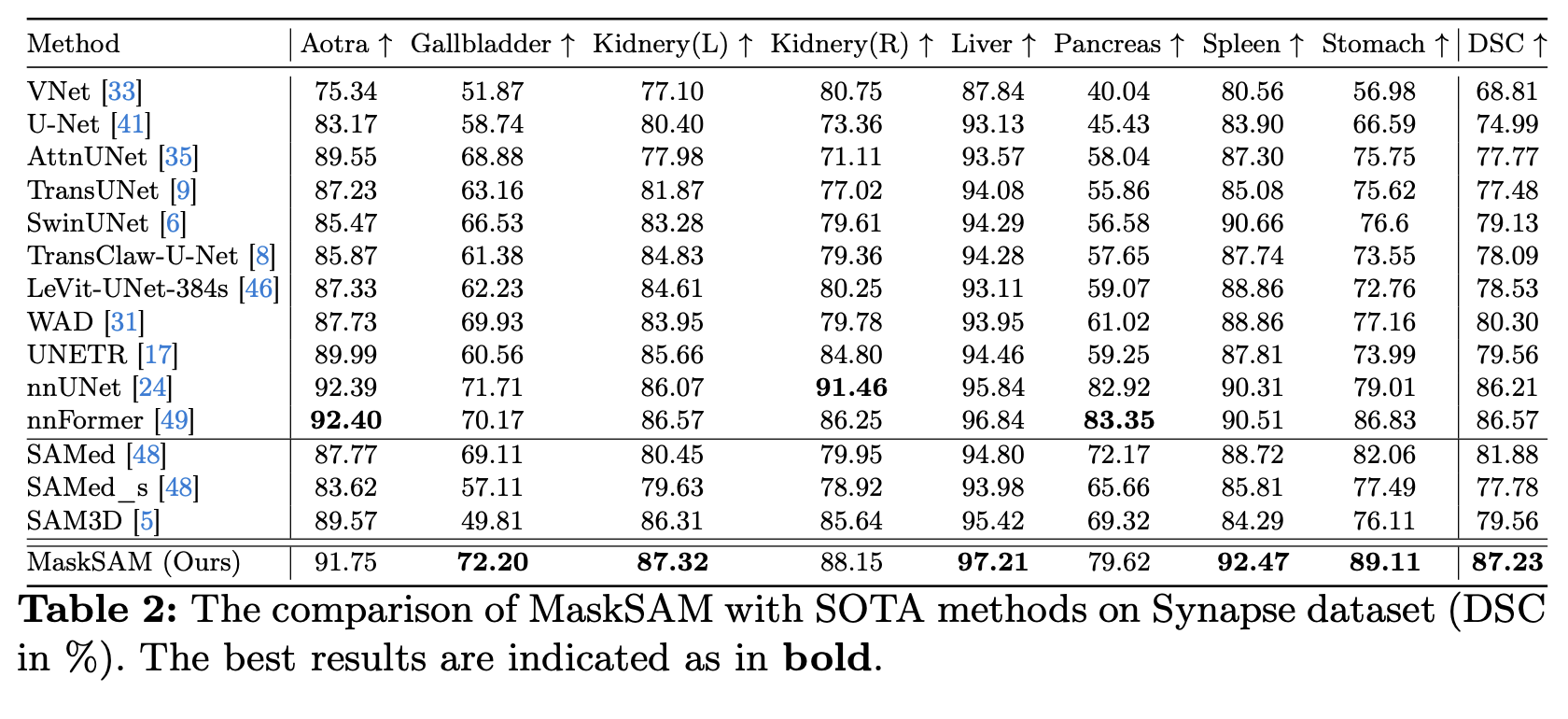
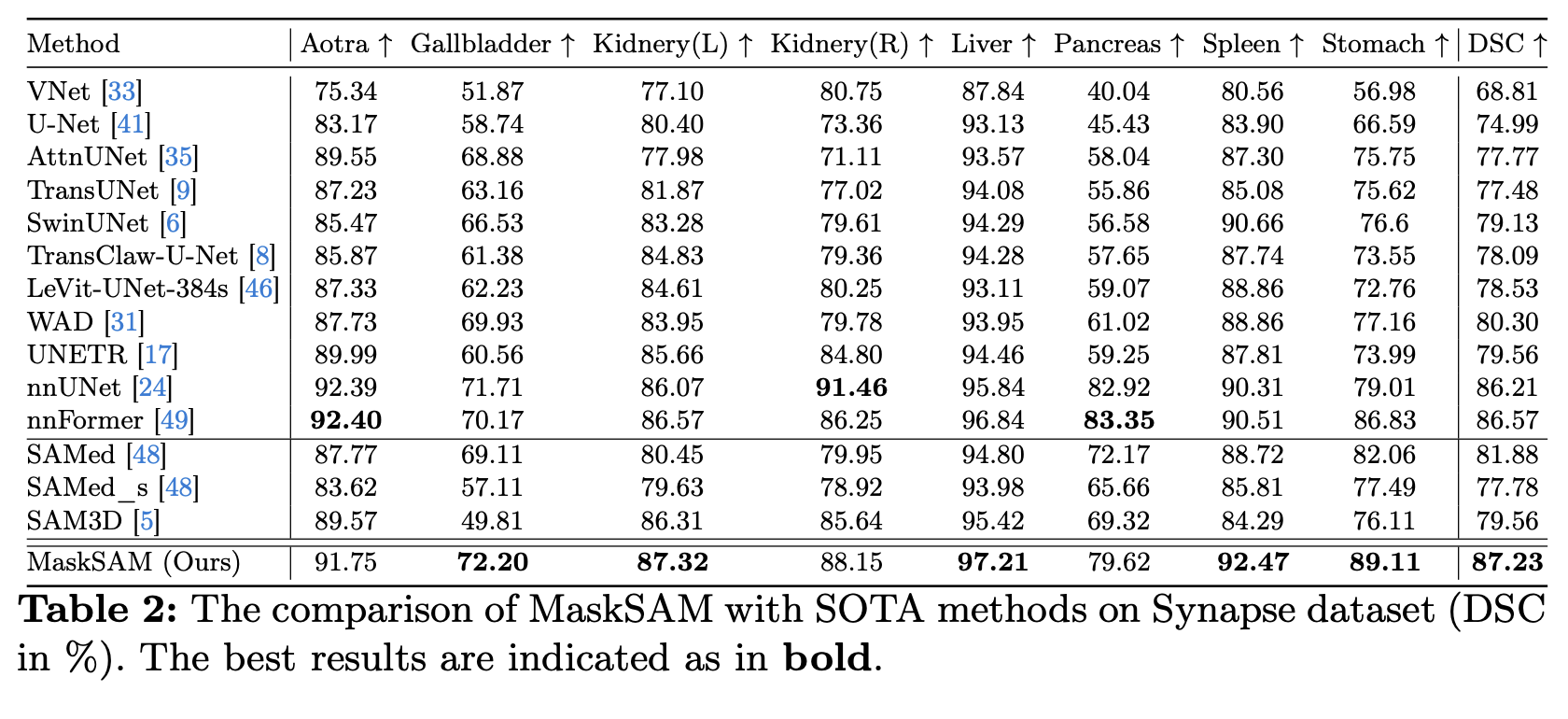
Ablation study 등 추가적인 내용은 원본 논문을 참고.