본 포스팅은 제가 읽었던 논문을 간단하게 정리하는 글입니다. 논문의 모든 내용을 작성하는 것이 아닌, 일부분만 담겨 있으므로 자세한 내용은 원본 논문을 확인해 주시기를 바랍니다. 또한, 논문을 잘못 이해한 부분이 있을 수 있으므로, 양해 바랍니다.

---

Abstract

최근, 정형 데이터를 위한 딥러닝 아키텍처가 연구되고 발표되고 있음. 여러 논문에서 새로 제안하는 모델과 기존 모델들 사이의 성능 비교를 제시하지만, 제안되는 모델들이 서로 제대로 비교되지 않는 경우가 많고, 서로 다른 벤치마크 및 실험 프로토콜을 사용하였음. 결과적으로, 어떤 모델이 가장 우수한지 알기 어려움. 또한, 다양한 문제에서 경쟁력 있는 성능을 제공하며 사용하기 쉬운 베이스라인 모델이 여전히 부족함.

이번 논문에서는 정형 데이터를 위한 주요 딥러닝 아키텍처들의 개요를 알아보고, 간단하고 강력한 딥러닝 아키텍처 2가지를 소개함으로 베이스라인의 기준선을 높이고자 함.

첫 번째 모델은 ResNet-like 구조로, 종종 강력한 베이스라인 모델로 소개되었음. 두 번째 모델은 트랜스포머 구조를 정형 데이터에 간단히 적용한 것으로, 대부분의 작업에서 뛰어난 성능을 발휘하였음.

두 모델을 다양한 작업에서 동일한 훈련 및 튜닝 프로토콜에 따라 기존의 아키텍처들과 비교하였음. 또한 가장 성능이 좋았던 딥러닝 모델을 Gradient Boosted Decision Trees와 비교하여, 보편적으로 우수한 모델은 없다는 결론을 내렸음.

Introduction

딥러닝은 이미지, 오디오, 텍스트 등 다양한 도메인에서 성공을 이루었고, 이러한 성공을 정형 데이터의 문제로 확장하려는 여러 연구가 진행되었음. 딥러닝의 잠재적인 더 높은 성능과 함께, 정형 데이터에 딥러닝을 적용하는 것은 multi-modal(정형 데이터 + 이미지, 오디오 등) 문제를 위한 파이프라인을 구성할 수 있어 매력적인 방법임. 이러한 파이프라인은 gradient 최적화를 통해 end-to-end 학습이 가능함. 이러한 이유로, 정형 데이터를 위한 딥러닝에 대한 연구가 계속되서 발표되고 있음.

하지만 정형 데이터에는 ImageNet, GLUE 등과 같이 확립된 벤치마크가 존재하지 않아 기존 논문들은 모델 간의 평가를 위해 서로 다른 데이터셋을 사용하였고, 새로 제안된 모델이 서로 적절히 비교되지 않는 경우가 많았음. 따라서 현재의 논문들을 보면 일반적으로 어떤 딥러닝 모델이 성능이 좋은지, 또한 GBDT가 딥러닝 모델을 능가하는지의 여부는 불분명함.

새로운 모델들이 계속 제안되고 있음에도, 이 분야는 여전히 적당한 노력으로 경쟁력 있는 성능을 달성할 수 있고 많은 작업에서 안정적인 성능을 제공하는 간단하고 신뢰할 수 있는 솔루션(베이스라인)이 부족함. 이런 측면에서 MLP는 여전히 이 분야의 간단한 베이스라인으로 남아있지만, MLP는 다른 모델들에게 어려운 기준선이 되지 않음.

이러한 문제를 기반으로, 이번 논문을 통해 최근 Deep tabular learning에 대한 연구 상황을 검토하고, 정형 데이터를 위한 딥러닝의 베이스라인 기준을 높이고자 함. 다른 분야에서 이미 검증된 아키텍처에서 영감을 얻어 두 가지 간단한 모델을 제안함. ResNet-like 모델과 트랜스포머 구조를 정형 데이터에 맞게 변형한 FT-Transformer 모델을 제안하며, 이 두 모델을 동일한 훈련 / 튜닝 과정하에 다양한 작업에서 기존 모델들과 비교하고자 함.

논문에서 고려된 어떠한 모델도 지속적으로 ResNet-like 모델을 능가할 수 없었음. ResNet-like의 단순한 구조를 생각해 보면, 이 모델은 향후 연구에 강력한 베이스라인이 될 수 있을 것임. 또한, FT-Transformer는 대부분의 작업에서 최고의 성능을 보여주어 강력한 솔루션이 되었음. 마지막으로 가장 좋은 성능의 딥러닝 모델과 GBDT를 비교하였을 때, 아직 보편적으로 우수한 모델은 없다는 결론을 내렸음.

본 논문의 주요 내용을 요약하면 다음과 같음.

• 다양한 set of tasks에서 정형 데이터를 위한 딥러닝 모델을 철저하게 평가하여 상대적인 성능을 조사함.
• 간단한 ResNet-like 모델이 효과적인 베이스라인이 될 수 있음을 입증함. 향후 연구의 베이스라인으로 ResNet-like 모델을 권장함.
• 새롭고 강력한 솔루션이 될 수 있는 FT-Transformer를 제안함. FT-Transformer는 광범위한 task에서 우수한 성능을 발휘한 보편적인 아키텍처임.
• 딥러닝 모델과 GBDT를 비교하였을 때, 아직까지 보편적으로 우수한 솔루션이 없다는 것을 확인함.

Related work

The “shallow” state-of-the-art

정형 데이터를 위한 “shallow” state-of-the-art 모델은 ML 경진 대회에서 일반적으로 가장 많이 선택되는 GBDT와 같은 결정 트리의 앙상블임. XGBoost, LightGBM, CatBoost 등 다양한 GBDT 라이브러리가 사용되고 있음. 이러한 구현은 세부적으로는 다르지만, 대부분의 작업에서 그 성능은 크게 다르지 않음.

최근 몇 년 동안 정형 데이터를 위한 딥러닝 모델이 많이 발표되었음. 이러한 모델의 대부분은 크게 아래의 세 가지 그룹으로 분류할 수 있음.

Differentiable trees

첫 번째 그룹은 결정 트리 앙상블의 강력한 성능에 영향을 받았음. 결정 트리는 미분 불가능하고 gradient 최적화가 불가능하기 때문에, end-to-end 파이프라인의 구성 요소로 사용될 수 없음. 이러한 문제를 해결하기 위해 트리 내부 노드의 결정 함수를 smooth 하여 전체 트리 함수와 트리 routing을 미분 가능하게 하는 연구가 발표되었음. 실험 결과, 이 계열의 방법은 일부 작업에서 GBDT를 능가하였지만, ResNet-like 모델을 일관되게 능가하지 못하였음.

Attention-based models

다양한 도메인에서 어텐션 기반 아키텍처가 성공함에 따라, 여러 연구자들은 정형 데이터에도 어텐션 기반 딥러닝 모델을 사용할 것을 제안하였음. 이번 실험에서, 적절히 튜닝된 ResNet-like 모델이 기존의 어텐션 기반 모델보다 뛰어나다는 것을 확인하였음.

Explicit modeling of multiplicative interactions

추천 시스템과 클릭률 예측에 대한 연구에서, MLP는 특성 간 multiplicative interaction을 모델링하는 데 적합하지 않다고 알려져 있음. 이러한 문제에 따라, 몇몇 연구는 MLP에 feature product를 통합하는 방법을 제안하였음. 실험 결과, 이러한 방법들은 적절히 튜닝된 베이스라인보다 성능이 좋지 않았음.

마지막으로, 본 논문에서는 위 3가지 카테고리에 속하지 않은 다른 아키텍처(Grownet, Self-normalizing neural networks) 또한 고려하였음.

Models for tabular data problems

이번 섹션에서는 주요 딥러닝 아키텍처에 대해 설명함. 사용하기 쉬운 베이스라인의 존재가 중요하므로, ResNet-like 모델과 FT-Transformer 모델을 설계할 때 DL building blocks을 재사용하려고 노력하였음.

Notation
이번 연구에서는 지도 학습 문제(이진 분류 / 다중 분류 / 회귀)만을 고려함. 전체 데이터셋을 train, val, test 세 종류로 분할하며, train은 훈련, val은 early stopping과 하이퍼파라미터 튜닝, test는 최종 평가에 사용함.

MLP

MLP 모델의 구조를 다음의 식으로 공식화함.

MLP($x$) = Linear(MLPBlock(. . .(MLPBlock($x$))))
MLPBlock($x$) = Dropout(ReLU(Linear($x$)))

ResNet

ResNet-like 모델의 구조를 다음의 식으로 공식화함.

ResNet($x$) = Prediction(ResNetBlock(. . .(ResNetBlock(Linear($x$)))))
ResNetBlock($x$) = $x$ + Dropout(Linear(Dropout(ReLU(Linear(BatchNorm($x$))))))
Prediction($x$) = Linear(ReLU(BatchNorm($x$)))

ResNetBlock에서, 출력에 입력을 더한 residual connection을 확인할 수 있음.

FT-Transformer

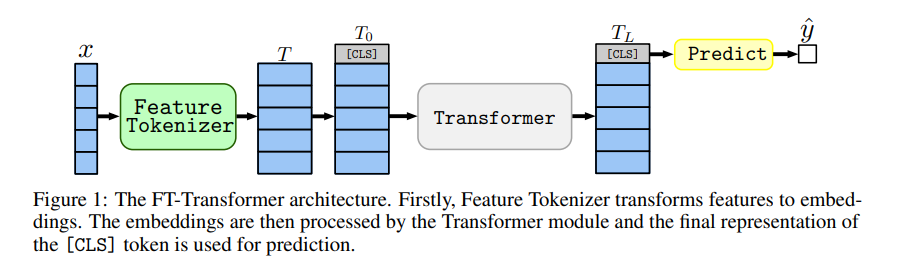
FT-Transformer(Feature Tokenizer + Transformer)는 정형 데이터를 위한 트랜스포머 아키텍처의 간단한 변형임. 모든 특성(범주형, 숫자형)을 Feature Tokenizer를 사용해 임베딩한 후 Transformer 모듈에 입력하여 처리함.

Feature Tokenizer

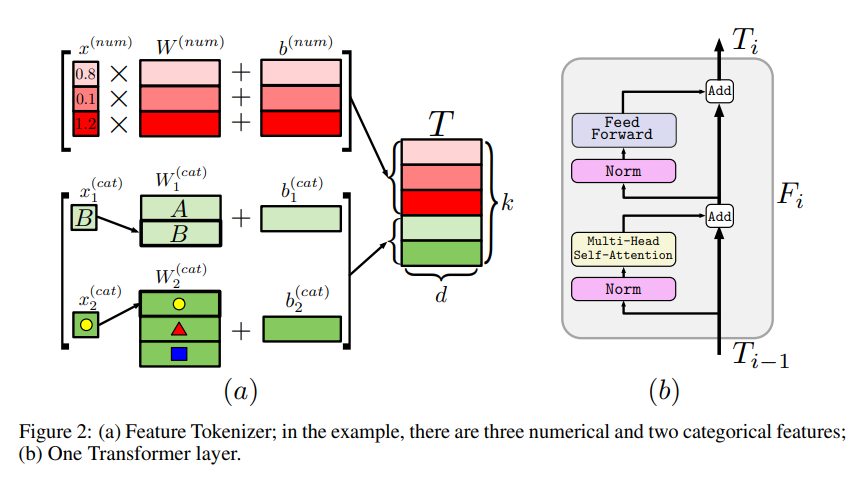
Feature Tokenizer는 입력 $x$를 임베딩 $T \in \mathbb R^{k \times d}$로 변환함. 주어진 특성 $x_j$에 대한 임베딩은 다음과 같이 계산됨: $T_j = b_j + f_j(x_j) \in \mathbb R^d \qquad f_j: \mathbb X_j \rightarrow \mathbb R^d$.

이때 $b_j$는 $j$번째 특성의 bias임. 결과적으로 종합하면 다음과 같음. 전체 특성의 개수를 $k$라고 정의함.

$T_j^{(\text{num})} = b_j^{(\text{num})} + x_j^{(\text{num})} \cdot W_j^{(\text{num})} \qquad \in \mathbb R^d$
$T_j^{(\text{cat})} = b_j^{(\text{cat})} + e_j^T W_j^{(\text{cat})} \qquad \in \mathbb R^d$
$T_j^{(\text{num})} = \text{stack} [T_1^{(\text{num})}, \cdots, T_{k^{(\text{num})}}^{(\text{num})}, T_1^{(\text{cat})}, \cdots, T_{k^{(\text{cat})}}^{(\text{cat})}] \qquad \in \mathbb R^{k \times d}$

$f_j^{(\text{num})}$은 벡터 $W_j^{(\text{num})}$에 대한 element-wise multiplication으로 구현되고, $f_j^{(\text{cat})}$은 lookup table $W_j^{(\text{cat})}$으로 구현됨. $e_j^T$는 해당 범주형 특성에 대응하는 one-hot 벡터임.

[CLS] 토큰의 임베딩을 $T$에 추가함. $T_0 = \text{stack} [[\text{CLS}], T]$이고, $L$개의 Transformer layer $F_1, \cdots , F_L$를 적용함. $T_i = F_i(T_{i-1})$

보다 쉬운 최적화를 위해 PreNorm variant를 사용함. PreNorm 설정에서, 좋은 성능을 위해 첫 번째 Transformer layer에서는 첫 번째 정규화를 제거해야 한다는 것을 발견함.

Prediction

[CLS] 토큰의 최종 representation이 예측에 사용됨.

$\hat y$ = Linear(ReLU(LayerNorm($T_L^{[\text{CLS}]}$)))

Limitations

FT-Transformer는 ResNet-like 모델보다 훈련에 더 많은 리소스를 필요로 하며, 특성의 개수가 너무 많은 데이터셋에는 적용하기 어려울 수 있음. 이러한 문제의 주요 원인은 특성 수에 대한 vanila Multi-Head Self-Attention (MHSA)의 quadratic complexity 때문임.

MHSA의 효율에 대한 문제는 MHSA의 근사치를 사용하여 문제를 완화할 수 있음. 또한, 더 나은 추론 성능을 위해 FT-Transformer를 간단한 아키텍처로 증류(distill)할 수 있음.

Other models

다음은 실험 비교에 사용된 모델들임.

SNN
SELU 활성화 함수를 포함한 MLP-like 아키텍처

NODE
미분 가능한 oblivious decision trees의 앙상블

TabNet
특성 선택과 피드포워드 모듈을 반복하는 아키텍처

GrowNet
weak MLPs의 Gradient boosting 모델

DCN V2
MLP-like 모듈과 특성 교차 모듈(a combination of linear layers and multiplications)로 구성

AutoInt
특성을 임베딩한 후 어텐션 기반 트랜스포머에 적용

XGBoost
GBDT implementation

CatBoost
oblivious decision tree를 weak learner로 사용한 GBDT implementation

Experiments

언급된 딥러닝 모델과 GBDT를 상호 비교함.

Scope of the comparison

다양한 아키텍처의 상대적 성능에 초점을 맞추며, 사전 학습 / 추가적인 손실 함수 / 데이터 증강 / 증류 / 학습률 감쇠 등의 model-agnostic DL practices를 적용하지 않음. 이러한 practices는 모델 성능을 향상시킬 수 있지만, 이번 논문의 목표는 다양한 모델 아키텍처에 부여된 귀납적 편향의 영향을 평가하는 것임.

Datasets

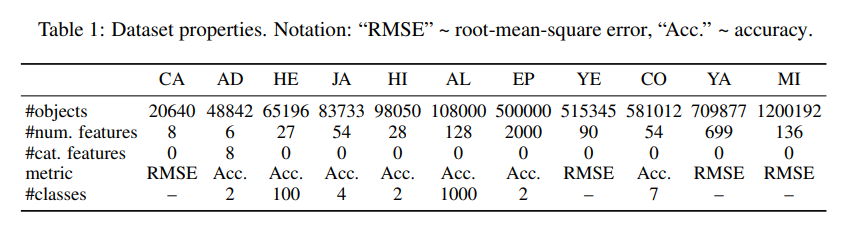
11개의 공개 데이터셋을 사용함. 각 데이터셋을 훈련-검증-테스트 데이터셋으로 분할함. 사용한 데이터셋은 다음과 같음.

• California Housing (CA, real estate data, Kelley Pace and Barry (1997))
• Adult (AD, income estimation, Kohavi (1996))
• Helena (HE, anonymized dataset, Guyon et al. (2019))
• Jannis (JA, anonymized dataset, Guyon et al. (2019))
• Higgs (HI, simulated physical particles, Baldi et al. (2014); we use the version with 98K samples available at the OpenML repository (Vanschoren et al., 2014))
• ALOI (AL, images, Geusebroek et al. (2005))
• Epsilon (EP, simulated physics experiments)
• Year (YE, audio features, Bertin-Mahieux et al. (2011))
• Covertype (CO, forest characteristics, Blackard and Dean. (2000))
• Yahoo (YA, search queries, Chapelle and Chang (2011))
• Microsoft (MI, search queries, Qin and Liu (2013))

각 데이터셋은 분류 또는 회귀를 위한 데이터셋임.

Implementation details

Data preprocessing
공정한 비교를 위해 모두 동일한 전처리 방법을 사용함. 기본적으로 사이킷런의 quantile transformation을 사용하였고, Helena와 ALOI에는 표준화(mean subtraction and scaling)를 적용함. Epsilon 데이터셋에 전처리를 적용할 경우 모델 성능에 악영향을 주었으므로 전처리를 진행하지 않았음.

회귀 문제의 타깃값($y$)의 경우, 표준화를 적용함.

Tuning
검증 데이터셋에서 가장 좋은 성능을 가진 조합을 최선의 하이퍼파라미터로 결정하며, 테스트 데이터셋은 튜닝에 사용하지 않음. 대부분의 경우 Optuna를 사용하여 베이지안 최적화를 수행하였고, 나머지의 경우 해당 논문에서 권장하는 사전 정의된 조합을 반복하였음.

Evaluation
튜닝된 모델에 대해, 서로 다른 랜덤 시드를 사용해 15번의 실험을 수행한 뒤 테스트 데이터셋에 대한 성능을 제시함. 일부 알고리즘의 경우 하이퍼파라미터를 튜닝하지 않은 기본 모델의 성능 또한 제시함.

Ensembles
각 모델에 대해, 각 데이터셋에서 15개의 단일 모델을 동일한 크기의 세 개의 분리된 그룹으로 나누고, 단일 모델들의 예측의 평균을 구하여 3개의 앙상블을 얻음.

Neural networks
분류 문제에는 크로스 엔트로피를, 회귀 문제에는 mse를 사용함. TabNet과 GrowNet의 경우 원래의 구현과 Adam optimizer를 사용함. 나머지 알고리즘의 경우 AdamW optimizer를 사용함. 또한, learning rate schedules를 사용하지 않음.

각 모델의 논문에서 배치 사이즈에 대한 특별한 지침이 있지 않은 한, 모든 알고리즘에 미리 정의된 배치 크기를 사용함. 검증 데이터셋에 대한 개선이 patience + 1 이상 없다면 학습을 종료하며, 모든 알고리즘에 대해 patience = 16로 설정함.

Categorical features
XGBoost의 경우 one-hot 인코딩을, CatBoost의 경우 자체 내장된 기능을 사용함. 신경망의 경우 모든 범주형 특징에 대해 동일한 차원의 임베딩을 사용함.

Comparing DL models

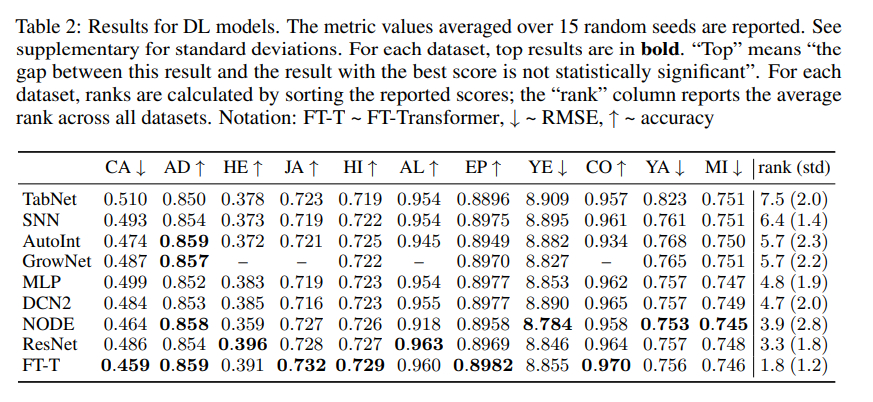
딥러닝 모델 간 성능 비교 결과는 다음과 같음.

• MLP는 여전히 준수한 성능을 보여줌.
• ResNet-like 모델은 어떤 모델도 지속적으로 능가할 수 없는 효과적인 베이스라인임.
• FT-Transformer는 대부분의 작업에서 최고의 성능을 보여주었음.
• 하이퍼파라미터 튜닝을 통해 MLP, ResNet-like 모델과 같은 단순한 모델도 경쟁력을 갖출 수 있음.

FT-Transformer를 제외하고, NODE 만이 여러 작업에서 좋은 성능을 보여주었음. 하지만 ResNet-like 모델보다 복잡한 구조임에도 불구하고 6개의 데이터셋에서 ResNet-like 모델보다 낮은 성능을 보여주었음.

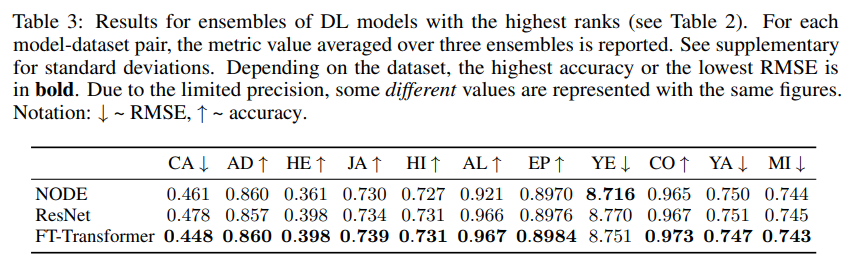
FT-Transformer와 ResNet-like 모델은 앙상블을 통해 더 많은 이점을 얻을 수 있음. 앙상블 결과, FT-Transformer는 NODE보다 성능이 뛰어나며 ResNet-like 모델은 NODE와의 격차가 줄어들었음. 그럼에도 불구하고 NODE는 트리 기반 접근 방식 중 여전히 두드러진 솔루션임.

Comparing DL models and GBDT

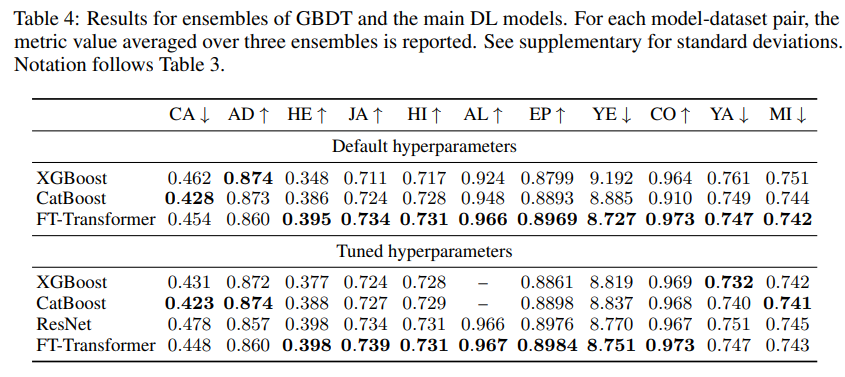
하드웨어 요구 사항과 속도를 고려하지 않고, GBDT와 딥러닝 모델을 사용하여 달성할 수 있는 최고의 성능을 비교함. GBDT는 기본적으로 앙상블 기술이므로 성능을 평가할 때 단일 모델 대신 앙상블을 사용하여 비교함.

모든 데이터셋에 대해, 기본 하이퍼파라미터와 튜닝된 하이퍼파라미터의 점수를 모두 비교함.

Default hyperparameters
CA, AD 데이터셋을 제외하고 FT-Transformer는 GBDT의 성능을 뛰어넘었음. 흥미롭게도 기본 FT-Transformer의 앙상블은 튜닝된 FT-Transformer의 앙상블과 거의 비슷한 성능을 발휘함.

Tuned hyperparameters
하이퍼파라미터가 적절히 튜닝되면, GBDT가 추가적으로 몇몇 데이터셋(California Housing, Adult, Yahoo)에서 우위를 점함. 이러한 경우, GBDT와 딥러닝 모델 사이의 격차가 충분히 커서 딥러닝 모델이 GBDT를 보편적으로 능가하지 못한다고 결론을 내릴 수 있음.

본 실험의 딥러닝 모델이 대부분의 작업에서 GBDT보다 성능이 뛰어나다고 해서, 딥러닝 솔루션이 어떤 의미에서든 더 낫다는 것은 아님. 이것은 구축된 벤치마크가 DL-friendly 문제에 약간 편향되어 있다는 것을 의미함. 물론, GBDT는 클래스가 많은 다중 분류 문제에는 여전히 부적절함. 클래스 수에 따라 GBDT는 만족스럽지 못한 성능을 보이거나(Helena), 매우 느린 훈련으로 하이퍼파라미터의 튜닝이 불가능할 수도 있음(ALOI).

An intriguing property of FT-Transformer

FT-Transformers는 GBDT가 ResNet-like 모델보다 우수한 문제에 대해서 ResNet-like 모델에 비해 대부분 더 나은 성능을 가졌고, 나머지 문제에 대해서는 ResNet-like 모델과 거의 동등한 성능을 가짐. 즉, FT-Transformer는 모든 작업에서 경쟁력 있는 성능을 제공하는 반면, GBDT와 ResNet-like 모델은 일부 하위 집합에서만 우수한 성능을 보여줌.

이러한 실험 결과는 FT-Transformer가 정형 데이터를 위한 보다 보편적인 모델이라는 증거일 수 있음. 이러한 현상은 앙상블과 관련 없으며, 단일 모델에서도 관찰되는 현상임.

Analysis

When FT-Transformer is better than ResNet?

FT-Transformer와 ResNet-like 모델 간 성능 차이의 원인을 이해하기 위해 실험을 진행함. 실험을 위해 sequence of synthetic tasks를 설계하는데, 두 모델의 성능 차이가 무시할 수 있는 수준에서 극적으로 변화하도록 설계함.

$n$개의 오브젝트 $x_i$를 생성한 뒤, 각 $x_i$에 해당하는 regression target $y$를 다음과 같이 생성함.

$y = \alpha \cdot f_{\text{GBDT}}(x) + (1 - \alpha) \cdot f_{\text{DL}}(x)$

$f_{\text{GBDT}}$는 GBDT에 더 쉬울 것으로 예상되는 매핑 관계이고, $f_{\text{DL}}$은 ResNet-like 모델에 더 쉬울 것으로 예상되는 매핑 관계임. $f_{\text{GBDT}}$는 무작위로 구성된 30개의 결정 트리의 평균 예측값이며, $f_{\text{DL}}$은 무작위로 초기화된 3개의 hidden layer를 가진 MLP의 예측값임.

타겟값은 모델 훈련 전 표준화되었고, 실험 결과는 다음과 같음.

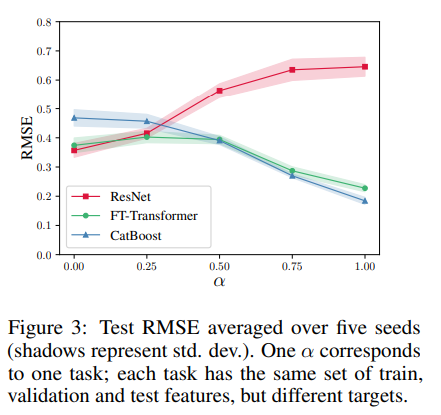
• ResNet-friendly 타겟에서, ResNet-like 모델과 FT-Transformer는 비슷한 성능을 보였으며 CatBoost 보다 성능이 우수하였음.
• 타겟이 GBDT-friendly가 되면 ResNet-like 모델의 상대적 성능이 크게 떨어짐.
• FT-Transformer는 전체 작업 범위에서 경쟁력 있는 성능을 제공하였음.

이 실험을 통해 FT-Transformer가 ResNet-like 모델보다 더 잘 근사화할 수 있는 함수 유형을 확인할 수 있음.

또한, 이러한 함수가 결정 트리를 기반으로 한다는 것은 An intriguing property of FT-Transformer 섹션의 관찰 결과와 모델 간 성능 비교 결과와 상관관계가 있음. GBDT가 ResNet-like 모델보다 성능이 뛰어난 데이터셋에서 FT-Transformer가 ResNet-like 모델에 비해 가장 확실한 개선을 보인다는 사실과도 일치함.

Ablation study

이번 섹션에서는 FT-Transformer의 몇 가지 디자인을 실험함. 첫 번째로, FT-Transformer와 가장 가까운 경쟁자라고 할 수 있는 AutoInt를 비교함. AutoInt 역시 모든 특성을 임베딩으로 변환하고 셀프 어텐션을 적용함. 그러나 세부적으로 다음과 같이 몇 가지 다른 점이 있음.

• AutoInt의 임베딩 layer는 feature bias를 사용하지 않음.
• AutoInt의 백본은 vanila Transformer와 크게 다름.
• 추론에 있어 [CLS] 토큰을 사용하지 않음.

두 번째로, 동일한 훈련 과정을 가진 feature bias가 없는 FT-Transformer의 성능을 확인하여 feature bias가 Feature Tokenizer에 필수적인지 확인함.

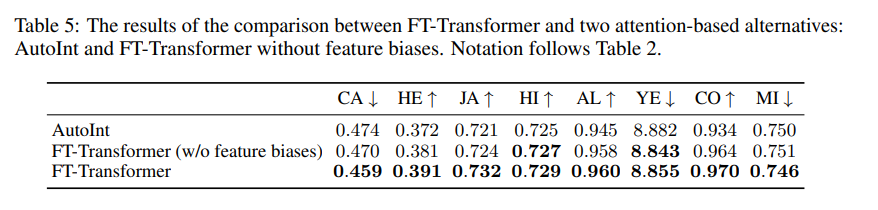
마찬가지로 15회의 테스트가 있었으며, 실험 결과 FT-Transformer의 Transformer 백본이 AutoInt 보다 우수하다는 것과 feature bias의 필요성을 모두 입증하였음.

Obtaining feature importances from attention maps

FT-Transformer의 어탠션 맵을 평가하여 주어진 데이터셋에 대한 특성 중요도로 사용할 수 있을지 확인함.

$i$번째 샘플에 대해, Transformer의 forward pass의 [CLS] 토큰을 사용하여 평균 어탠션 맵 $p_i$를 계산함. 그런 다음, 개별 분포를 평균화하여 특성 중요도를 나타내는 분포 $p$를 계산함.

$p = \frac{1}{n_{\text{samples}}} \sum_i p_i \qquad p_i = \frac{1}{n_{\text{heads}} \times L} \sum p_{ihl}$

$p_{ihl}$은 $i$번째 샘플의 $l$번째 Transformer layers, $h$번째 헤드의 [CLS] 토큰의 어탠션 맵임. 이러한 기법의 큰 장점은 효율성임. 모델 내부에 존재하는 한 번의 forward pass만으로 계산할 수 있음.

이러한 접근 방법을 평가하기 위해, 어탠션 맵과 Integrated Gradients(IG)를 비교함. 모든 데이터셋에 permutation test를 수행하여 모델의 해석 능력을 확인함.

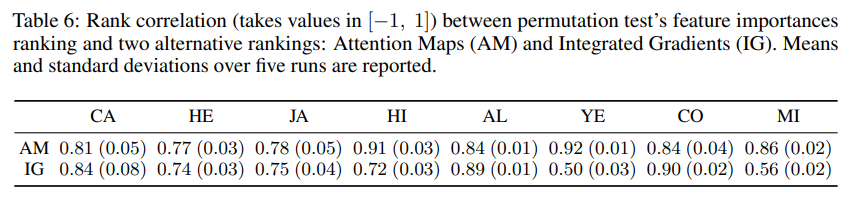
제안된 어탠션 맵 기반 방법은 합리적인 특성 중요도를 산출하였고, IG와 유사하게 작동하였음. IG의 느린 계산 속도와 계산 비용을 고려하였을 때, 어탠션 맵 기반의 단순 평균 방법이 비용 효율성 측면에서 좋은 선택이 될 수 있음.

Conclusion

본 논문을 통해 정형 데이터를 위한 딥러닝 연구의 현주소를 조사하고, 정형 데이터에서의 베이스라인의 기준선을 개선하였음. 간단한 ResNet-like 아키텍처는 효과적인 베이스라인 역할을 할 수 있으며, 제안한 FT-Transformer는 대부분의 작업에서 뛰어난 성능을 보여주었음. 또한 GBDT와의 성능 비교를 진행하였으며, 일부 작업에는 여전히 GBDT가 우세함을 확인함.

Supplementary material

Software and hardware

모든 실험은 같은 소프트웨어 버전과 하드웨어에서 수행되었음.

Data

회귀 문제에 대해서, 타겟값 $y$를 표준화하였음. 딥러닝 모델을 위한 전처리는 본문 내용에서 확인할 수 있음. features with few distinct values에 대하여, quantile preprocessing의 매개변수(quantiles)를 계산할 수 있도록 $N(0, 1e-3)$의 노이즈를 훈련 데이터의 숫자형 특성에 추가하였음. GBDT에 대해서는 별다른 전처리를 진행하지 않았음.

Results for all algorithms on all datasets

통계적 유의성을 확인하기 위해 one-sided Wilcoxon test with p = 0.01 검정을 수행함.

Additional results

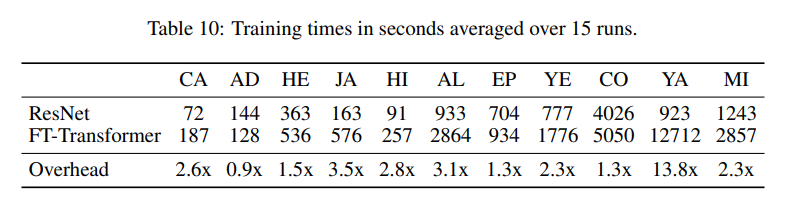
ResNet-like 모델과 FT-Transformer의 훈련 시간 차이를 확인할 수 있음. 특성의 개수가 많은 경우(YA), 훈련 시간의 차이가 매우 크게 남.

훈련 시간에 따른 성능 차이를 비교하고자, XGBoost, MLP, ResNet-like, FT-Transformer 4개의 모델을 사용하여 실험을 진행함. California Housing, Adult, Higgs Small 3개의 데이터셋을 사용하였으며, 각 데이터셋마다 5번의 독립적인 하이퍼파라미터 최적화를 수행함.

15분, 30분, 1시간, 2시간, 3시간, 4시간, 5시간, 6시간 동안 하이퍼파라미터를 튜닝한 뒤 성능을 확인함. 모델의 성능과 함께 Optuna의 반복 횟수 또한 확인함(5개 랜덤 시드에 대한 평균값). 실험 결과는 다음과 같음.

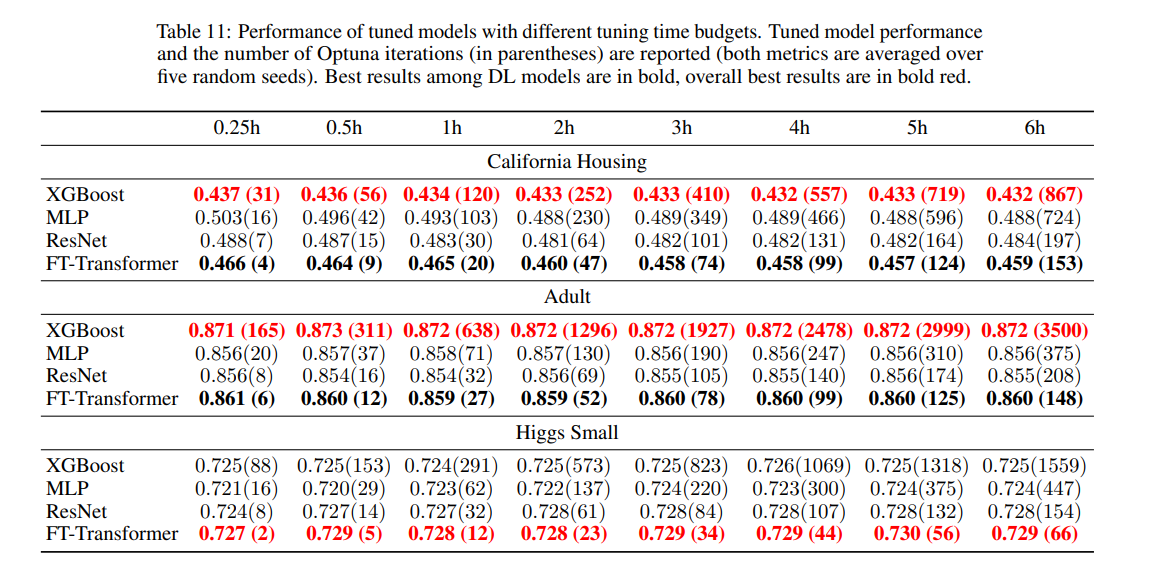
• FT-Transformer는 무작위로 샘플링된 구성에서 좋은 결과를 얻음(Optuna는 처음 10회 동안 simple random sampling을 수행함).
• FT-Transformer는 훈련에 오랜 시간이 걸림.
• Optuna의 반복 횟수가 올라가도 유의미한 개선이 생기지 않았음.

FT-Transformer

MLP, ResNet-like처럼, FT-Transformer도 다음과 같이 공식화할 수 있음.

FT-Transformer($x$) = Prediction(Block(. . .(Block(AppendCLS(FeatureTokenizer($x$))))))
Block($x$) = ResidualPreNorm(FFN, ResidualPreNorm(MHSA, $x$))
ResidualPreNorm(Module, $x$) = $x$ + Dropout(Module(Norm($x$)))
FFN($x$) = Linear(Dropout(Activation(Linear($x$))))

정규화를 위해 LayerNorm를 사용하였으며, MHSA에서는 $n_{\text{heads}}=8$을 적용함. ReGLU 활성화함수를 사용하였고, 간단하고 동일한 최적화를 위해 PreNorm을 사용함(Transformer 원본은 PostNorm을 사용함).

Analysis

When FT-Transformer is better than ResNet?
가상의 데이터들은 $x \sim N(0, I_{100})$의 분포를 가진 100차원의 데이터로 생성되었으며, 훈련 데이터 500,000개, 검증 데이터 50,000개, 테스트 데이터 100,000개의 샘플이 생성됨. 각 데이터 샘플의 경우 앞에서 50개의 특성만이 타겟 $y$를 생성하는데 사용되었고, 나머지 50개의 특성은 노이즈의 역할을 함.

---

Attention Map?

Obtaining feature importances from attention maps에서, IG와 어탠션 맵의 특성 중요도를 비교하는 실험 과정이 자세히 적혀 있지 않아 나름의 추론 후 추가적인 글을 작성합니다.

논문에서 Rank correlation을 계산하기 위해 permutation test를 진행하였는데, 언급된 permutation test의 레퍼런스가 Random Forests 논문이므로 랜덤 포레스트에서 특성 중요도를 구할 때 사용한 방법(OOB permutation)과 비슷하게 특성 중요도를 계산한 것 같습니다.

공식 코드나 추가적인 자료에도 자세한 실험 과정이 적혀 있지는 않지만, 랜덤 포레스트의 permutation, "performs similarly to IG (note that this does not imply similarity to IG’s feature importances), Means and standard deviations over five runs are reported." 이라는 논문 내 내용, 그리고 각 데이터셋에 대해 AM, IG의 Rank correlation이 모두 적혀있는 점(e.g. CA: AM(0.81), IG(0.84))을 고려하여 유추해 본 특성 중요도 비교 실험 과정은 다음과 같습니다.

• 원래 데이터셋에 대해 AM, IG 방법으로 특성 중요도를 계산한 뒤, 순위(rank)를 계산한다.
• 임의의 한 특성을 permutation 한 후, 두 방법으로 특성 중요도를 다시 계산하여 순위를 계산한다.
• 각 방법 AM, IG에 대해, 원래 데이터셋과 permutation 데이터셋의 순위를 사용하여 correlation을 계산한다.
• (논문의 방법) 5번의 반복 후 평균과 표준편차를 작성한다.

위와 같은 방법을 통해 AM, IG가 유사한 방식으로 작동함을 확인하였다고 생각합니다. 간단한 예시를 들어보겠습니다.

전체 특성의 개수가 3개인 데이터셋을 가정합니다. 특성 a, b, c에 대해서, AM과 IG를 통해 계산한 특성 중요도 순위가 다음과 같다고 하겠습니다.

• AM: a(1), b(2), c(3), IG: a(1), b(2), c(3)

즉 두 방법의 특성 중요도가 같습니다(AM과 IG가 유사하게 작동합니다). 이제, 특성 중요도가 가장 높은 특성 a를 permutation 한 후, 다시 특성 중요도 순위를 계산하였다고 하겠습니다. 가장 중요한 특성이 permutation 되었을 것이므로 모델에 큰 영향을 줄 것이며, 특성 중요도가 떨어질 것입니다. 특성 중요도 순위가 다음과 같이 변했다고 생각하겠습니다.

• AM': a(3), b(1), c(2), IG': a(3), b(1), c(2)

이때 AM과 AM', IG와 IG' 사이의 순위 상관관계를 계산해 보면(Jamovi를 사용하여 계산하였습니다), 두 경우 모두 -0.50의 값을 가집니다.

반대로, 특성 a가 아닌 특성 중요도가 가장 낮은 특성 c를 permutation 한 후 다시 특성 중요도를 계산합니다. 가장 특성 중요도가 낮으므로, permutation의 영향이 적을 것이며 특성 중요도의 변화가 없을 것입니다. 이 경우는 AM과 AM', IG와 IG'의 순위 상관관계가 모두 1.00입니다. 요약하면, AM 기반 특성 중요도 계산 방법과 IG 기반 특성 중요도 계산 방법이 비슷하게 동작한다면 계산되는 순위 상관관계가 어떤 값을 가지던 비슷한 값을 가집니다.

반대로, AM과 IG가 정반대의 방법으로 특성 중요도를 계산한다고 가정하겠습니다. 특성 a, b, c에 대해서, AM과 IG를 통해 계산한 특성 중요도 순위가 다음과 같다고 하겠습니다.

• AM: a(1), b(2), c(3), IG: a(3), b(2), c(1)

AM이 가장 중요하다고 판단한 특성을 IG는 가장 덜 중요하다고 판단하였습니다. 즉, AM과 IG는 유사하게 작동하지 않습니다(논문의 저자가 바라지 않는 상황입니다). 이때 특성 a를 permutation 하고 특성 중요도를 계산합니다. AM의 경우, 특성 a는 가장 중요한 특성이므로 특성 중요도 순위에 큰 변화가 있을 것입니다. 반대로 IG는 가장 덜 중요한 특성이므로 변화가 없을 것입니다. 새로 계산된 특성 중요도가 다음과 같다고 하겠습니다.

• AM': a(3), b(1), c(2), IG': a(3), b(2), c(1)

이 경우, AM과 AM', IG와 IG' 사이의 순위 상관관계를 계산해 보면 AM은 -0.50, IG는 1.00이 계산됩니다. 반대로 특성 c를 permutation 한다면 AM이 1.00, IG는 -0.50이 계산될 것입니다.

정리하자면, AM과 IG가 유사하게 특성 중요도를 계산한다면(계산된 특성 중요도가 값이 같다는 것이 아닌, 중요도의 순서가 같은 경우) rank correlation이 서로 비슷한 값을 가지게 될 것이고, AM과 IG가 서로 상이하게 특성 중요도를 계산한다면 rank correlation은 서로 상이한 값을 가질 것입니다.

논문의 실험 결과를 보면, 대부분의 데이터셋에서 AM과 IG는 서로 비슷한 값을 가지고 있습니다. 이는 AM과 IG가 유사하게 특성 중요도를 계산한다는 것으로 생각할 수 있겠습니다. 즉, simple averaging of attention maps가 특성 중요도로써 사용될 수 있음을 뜻합니다.