---

본 포스팅은 제가 읽었던 논문을 간단하게 정리하는 글입니다. 논문의 모든 내용을 작성하는 것이 아닌, 일부분만 담겨 있으므로 자세한 내용은 원본 논문을 확인해 주시기를 바랍니다. 또한, 논문을 잘못 이해한 부분이 있을 수 있으므로, 양해 바랍니다.

ABSTRACT

오늘날 DNN은 CV, NLP, speech 등 다양한 도메인에서 주요 도구로 사용되고 있으나, 정형 데이터에서의 DNN의 장점은 여전히 의문시되고 있음. 딥러닝 모델이 정형 데이터에서 가장 많이 사용되는 GBDT를 능가할 수 있다는 충분한 증거가 존재하지 않음.

본 논문에서는 모든 정형 데이터에서 사용할 수 있는 새로운 Deep Tabular Model인 Neural Oblivious Decision Ensembles (NODE)를 소개함.

NODE 아키텍처는 oblivious decision trees의 앙상블을 일반화하며, gradient 기반의 end-to-end 방식과 multi-layer hierarchical representation learning의 장점을 모두 활용함.

많은 데이터셋에서 GBDT 패키지와 실험한 결과, 대부분의 작업에서 경쟁자보다 좋은 성능을 확인할 수 있었음. NODE의 PyTorch 구현을 오픈소스로 구현하였으며, 정형 데이터를 위한 보편적인 프레임워크가 될 것이라고 기대함.

INTRODUCTION

역전파를 사용한 gradient 기반 최적화, 계층적 표현 학습은 머신러닝 모델의 성능을 크게 향상시켰고, 최근 DNN은 CV, NLP, Speech Recognition 등 다양한 도메인에서 좋은 성능을 보여주고 있음.

다양한 영역에서의 deep architectures의 우수성을 의심할 여지가 없지만, 정형 데이터에 대한 머신러닝은 여전히 DNN의 이점을 충분히 활용하지 못함. 흔히 SOTA라 불리는 정형 데이터에서의 최첨단 성능은 GBDT와 같은 "shallow" 모델을 통해 달성되는 경우가 많음.

정형 데이터를 위한 딥러닝의 중요성은 많은 사람들이 인식하고 있으며, 많은 연구에서 이러한 문제를 다르고 있으나 아직까지 일관되게 우수한 성능을 발휘하는 아키텍처는 존재하지 않음.

본 논문에서는 정형 데이터를 위한 새로운 아키텍처, Neural Oblivious Decision Ensembles(NODE)를 소개함. NODE는 CatBoost에서 영감을 받았음.

CatBoost는 oblivious decision trees에 대해 gradient boosting을 수행하며, 추론이 매우 효율적이고 과대적합을 억제할 수 있음. 본질적으로 NODE는 CatBoost를 일반화하며, 분할 특성 선택과 결정 트리 routing을 미분가능하게 함. 또한, NODE는 multi-layer architectures를 사용하여 end-to-end 방식으로 훈련된 deep GBDT와 같은 구조를 구축할 수 있음.

oblivious decision trees 외에도, 중요한 design choice는 entmax 변환임. 이는 NODE 내부의 결정 트리에서 ”soft” splitting feature choice를 효과적으로 수행함.

많은 실험을 통해, NODE가 경쟁자(GBDT)보다 더 일관적으로 우수한 성능을 보였음을 확인함.

이번 논문을 다음과 같이 요약할 수 있음.

1. 정형 데이터를 위한 새로운 DNN 아키텍처를 제안
2. 실험을 통해 NODE가 기존 GBDT 구현보다 성능이 뛰어남을 확인
3. NODE의 PyTorch 구현을 오픈소스로 사용 가능

RELATED WORK

The state-of-the-art for tabular data

정형 데이터에서 가장 많이 사용되는 것은 GBDT, Random Forest와 같은 결정 트리의 앙상블임. XGBoost, LightGBM, CatBoost와 같은 GBDT 패키지들이 널리 사용되고 있음. 이러한 패키지들은 세부적으로는 다르지만, 대부분의 작업에서 비슷한 성능을 보여줌.

CatBoost의 가장 중요한 차이점은 약한 학습자로 oblivious decision trees (ODTs)를 사용하는 것임. ODTs는 NODE의 중요한 구성 요소이기도 함.

Oblivious Decision Trees

oblivious decision tree는 동일한 깊이의 모든 내부 노드에서 동일한 분할 특성과 분할 임계값을 사용하도록 제약된 깊이 $d$의 트리임. 이러한 제약은 ODT가 일반적인 결정 트리보다 훨씬 약한 학습자가 되게 함.

앙상블에서 이러한 트리를 사용하게 되면 과대적합이 덜 발생하는 것을 확인하였으며, ODT의 추론은 매우 효율적임.

Differentiable trees

트리 기반 방법의 가장 큰 단점은 일반적으로 end-to-end 기반 최적화를 지원하지 않으며, 트리 구성을 위해 greedy한 lcoal 최적화 절차를 사용한다는 것임. 이러한 단점으로 인해 트리 기반 방법은 end-to-end 방식으로 학습된 파이프라인의 구성 요소로 사용할 수 없었음.

이러한 문제를 해결하기 위해 여러 연구에서 내부 트리 노드의 결정 함수를 soften 하어 전체적인 트리 함수와 트리 라우팅을 미분가능하게 하는 것을 제안함.

이번 논문에서는 결정 트리를 soften 하기 위해 최근 발표된 entmax 변환을 사용함. 이러한 접근 방법은 이전의 접근 방법에 비해 장점이 있음을 실험을 통해 확인하였음.

Entmax

entmax 변환은 실수값 score 벡터를 이산 확률 분포에 매핑함. 이 변환은 softmax와 sparsemax를 일반화한 것임.

entmax는 대부분의 확률이 0과 같은 희소 확률 분포를 생성할 수 있음. 이번 논문에서는 entmax가 NODE에 대해 적절한 귀납적 편향을 제공하는 것으로 주장함.

직관적으로, entmax는 데이터 특성의 하위 집합을 기반으로 분할 결정을 학습할 수 있으며 다른 요소로부터 원치 않는 영향을 피할 수 있음.

추가적으로, 특성 선택에 entmax를 사용하면 미리 계산된 희소 선택 벡터를 사용하여 효율적으로 추론할 수 있음.

Multi-layer non-differentiable architectures

랜덤 포레스트, GBDT와 같이 미분 불가능한 블럭을 사용하여 multi-layer 구조를 구축하는 연구가 존재함.

최근 연구에서는 multi-layer GBDT를 도입하고 각 계층 구조가 미분가능할 필요가 없는 훈련 절차를 제안함.

이와 반대로, 본 논문은 end-to-end 훈련이 중요하다고 주장하며, 실험을 통해 이 주장을 확인함.

Specific DNN for tabular data

많은 선행 연구에서 정형 데이터를 위해 설계된 아키텍처를 제안하지만, 대부분 적절한 기준선-적절히 튜닝된 GBDT와 비교하지 않았음. NODE는 많은 수의 데이터셋에서 튜닝된 GDBT를 일관되게 능가하는 최초의 접근 방식임.

NEURAL OBLIVIOUS DECISION ENSEMBLES

DIFFERENTIABLE OBLIVIOUS DECISION TREES

NODE의 중요 빌딩 블럭은 Neural Oblivious Decision Ensemble (NODE) layer임. 이 layer는 깊이 $d$의 미분 가능한 $m$개의 ODTs로 구성됨. 모든 $m$개의 트리는 일반적인 벡터 $x \in \mathbb R^n$을 입력받으며, $n$은 숫자형 특성의 개수임.

본질적으로, ODT는 데이터를 $d$개의 분할 특성으로 데이터를 분할하고 임계값과 비교하는 decision table임. 그런 다음, 트리는 비교 결과에 해당하는 $2^d$개의 가능한 응답 중 하나를 반환함.

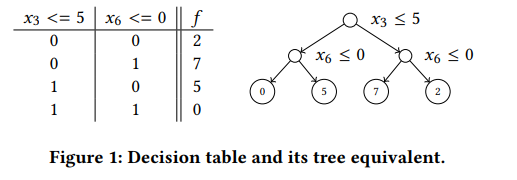
(Source: BDT - Gradient Boosted Decision Tables for High Accuracy and Scoring Efficiency)

따라서, 개별 ODT는 분할 특성 $f \in \mathbb{R}^d$, 분할 임계값 $b \in \mathbb{R}^d$, $d$차원의 response 텐서 $R$에 의해 완전히 결정됨.

트리의 출력은 다음의 수식으로 작성할 수 있음.

$h(x) = R[\mathbb{1}(f_1(x)-b_1), \cdots, \mathbb{1}(f_d(x)-b_d)]$

이때 $\mathbb{1}(\cdot)$은 Heaviside 함수로, 단위 계단 함수를 의미함(0보다 작은 실수는 0, 0보다 큰 실수는 1, 0에 대해서 0.5를 갖는 함수)

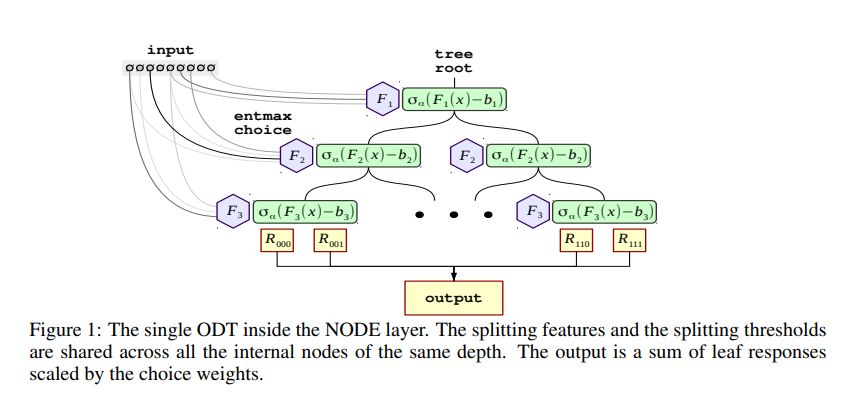
트리의 출력을 미분 가능하게 하기 위해, 분할 특징 선택 $f_i$와 비교 연산자 $\mathbb{1}(f_i(x) - b_i)$를 연속적인 것으로 대체함. 결정 트리의 미분가능한 선택 함수에 대한 여러 연구가 있었지만, 기존의 접근 방식은 일반적으로 긴 훈련 시간이 필요하여 실제 적용에 문제가 될 수 있음.

그 대신, 기본적인 경사 하강법을 사용하여 sparse choice를 학습할 수 있는 $\alpha$-entmax 변환을 사용함. 따라서, 선택 함수는 특성 간 weighted sum으로 대체되며, 각 가중치는 학습 가능한 특성 선택 행렬 $F \in \mathbb{R}^{d \times n}$에 대해 entmax로 계산된 가중치임.

$\hat f_i(x) = \sum_{j=1}^n x_j \cdot \text{entmax}_\alpha(F_{ij})$

다음으로, Heaviside 함수를 two-class entmax $\sigma_\alpha(x) = \text{entmax}_\alpha(\lfloor x, 0 \rfloor)$로 완화함. 특성 사이 스케일이 다를 수 있으므로, 스케일된 버전 $c_i(x) = \sigma_\alpha(\frac{f_i(x)-b_i}{\tau_i})$를 사용하며, $b_i, \tau_i$ 모두 학습 가능한 임계값과 스케일 값임.

$c_i(x)$를 기반으로, choice 텐서 $C$를 정의함. 이는 response 텐서 $R$와 동일한 크기를 가짐. $C$는 모든 $c_i$의 outer product로 계산함.

$C(x) = \begin{bmatrix} c_1(x)\\1-c_1(x) \end{bmatrix} \otimes \begin{bmatrix} c_2(x)\\1-c_2(x) \end{bmatrix} \otimes \cdots \otimes \begin{bmatrix} c_d(x)\\1-c_d(x) \end{bmatrix}$

최종 예측은 response 텐서 $R$과 choice 텐서 $C$의 가중치가 적용된 선형 조합으로 계산됨.

$\hat h(x) = \sum_{i_1, \cdots, i_d \in \{0, 1\}^d} R_{i_1, \cdots , i_d} \cdot C_{i_1, \cdots , i_d}(x)$

마지막으로, NODE layer의 출력은 $m$개의 개별적 출력을 연결한 것으로 구성됨.

$\begin{bmatrix} \hat h_1(x), \cdots, \hat h_m(x) \end{bmatrix}$

GOING DEEPER WITH THE NODE ARCHITECTURE

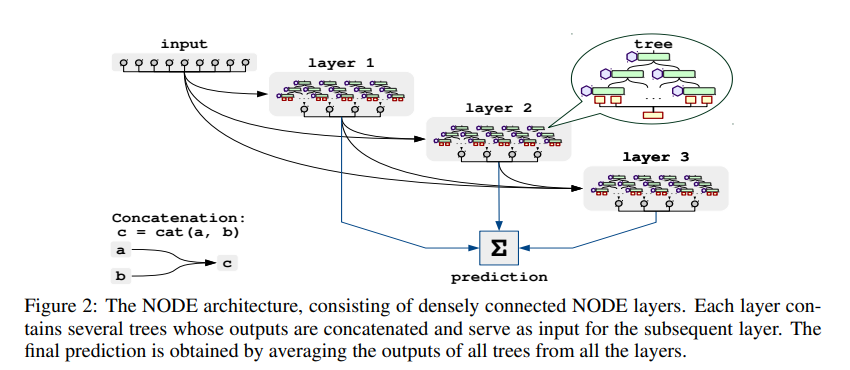
NODE layer는 단독 또는 복잡한 구조 내에서 훈련될 수 있으며, multi-layer 구조로 구성할 수도 있음. 이번 논문에서는 DenseNet 모델을 따르는 새로운 아키텍처(Concatenation)를 도입하고 역전파를 통해 훈련시킴.

DenseNet과 유사하게, NODE는 $k$개의 NODE layer를 가지며 각 레이어는 모든 이전 레이어의 연결(concatenation)을 입력으로 사용함. 이러한 설계를 통해 shallow, deep 의사 결정 규칙을 모두 학습할 수 있음. $i$번째 layer의 단일 트리는 최대 $i-1$개의 layer 출력 체인을 특성으로 사용할 수 있으므로 복잡한 종속성을 포착할 수 있음.

결과 예측은 모든 layer의 모든 결정 트리의 단순 평균임.

TRAINING

training protocol은 다음과 같음.

Data preprocessing
사이킷런의 quantile transform을 사용하여 특성 변환 수행. 실험에서, quantile transform을 적용하는 단계가 안정적인 학습과 빠른 수렴을 위해 중요하다는 것을 확인함.

Initialization
좋은 초기 파라미터 값을 얻기 위해 data-aware initialization을 수행함. 특징 선택 행렬 $F$는 균일하게 $U(0,1)$로 초기화하고, 임계값 $b$는 첫 번째 데이터 배치에서 관찰된 임의의 특성 값 $f_i(x)$로 초기화함. $\tau_i$ 첫 번째 배치의 모든 샘플이 $\sigma_\alpha$의 선형 영역에 속하도록 초기화되어 0이 아닌 기울기를 받도록 함. response 텐서 $R$는 표준 정규 분포 $N(0,1)$로 초기화됨.

Training
미니 배치 SGD를 사용하여 end-to-end 방식으로 학습하며, 모든 파라미터를 공동으로 최적화함. 전통적인 손실 함수(cross-entropy, mse)를 사용하였지만, 미분 가능한 다른 함수도 사용할 수 있음. optimizer로 Quasi-Hyperbolic Adam을 사용하였으며, 5개의 연속된 체크포인트에 대해 모델 파라미터의 평균을 구하고 검증 데이터셋을 사용해 최적의 중지 지점을 선택함.

Inference
훈련 중에는 entmax 함수를 계산하고 choice 텐서를 곱하는 과정에 상당한 시간이 필요함. 모델이 학습되면, entmax feature selectors를 미리 계산하고 이를 희소 벡터로 저장하여 추론을 더욱 효율적으로 수행할 수 있음.

EXPERIMENTS

COMPARISON TO THE STATE-OF-THE-ART.

다양한 데이터셋에서 NODE 아키텍처와 GBDT를 비교함. 모든 실험에서, entmax 변환의 $\alpha$ 값을 1.5로 설정하였음.

Datasets

총 6개의 데이터셋(Epsilon, YearPrediction, Higgs, Microsoft, Yahoo, Click)을 사용하여 실험을 수행하였음. 모든 데이터셋은 훈련/테스트 데이터셋으로 분할 되었으며, 훈련 데이터셋의 20%를 검증 데이터로 사용하여 하이퍼파라미터 튜닝에 사용하였음.

분류 문제의 경우 cross-entropy를 최소화하는 방향으로, 회귀 문제의 경우 mse를 최소화하는 방향으로 학습을 진행하였음.

Methods

NODE 아키텍처와 다음의 모델들을 비교함.

CatBoost
The recent GBDT implementation that uses oblivious decision trees as weak learners.

XGBoost
The most popular GBDT implementation widely used in machine learning competitions.

FCNN
Deep neural network, consisting of several fully-connected layers with ReLU nonlinearity layers.

Regimes

다음의 두 경우에서 실험을 진행함

Default hyperparameters
트리의 개수(XGBoost, CatBoost)를 제외한 하이퍼파라미터를 튜닝하지 않고 기본 옵션만을 사용하여 성능을 측정함. 이 실험에서는 FCNN을 고려하지 않았음. NODE의 경우 깊이 6의 2,048개의 결정 트리가 있는 단일 layer만 포함되어 있음. 단일 layer, 즉 shallow한 구조를 가지지만 여전히 역전파를 통한 end-to-end 학습의 이점을 누릴 수 있음.

Tuned hyperparameters
검증 데이터셋을 사용하여 하이퍼파라미터를 튜닝함. NODE의 경우, 2개에서 8개 사이의 NODE layer를 포함하며 모든 layer에 걸친 총 트리 수는 2,048개를 초과하지 않음.

Result

실험 결과는 다음과 같음. 10번의 서로 다른 랜덤 시드를 사용한 뒤 평균과 표준편차를 제시함. 분류 문제의 경우 classification error, 회귀 문제의 경우 mse를 의미함.

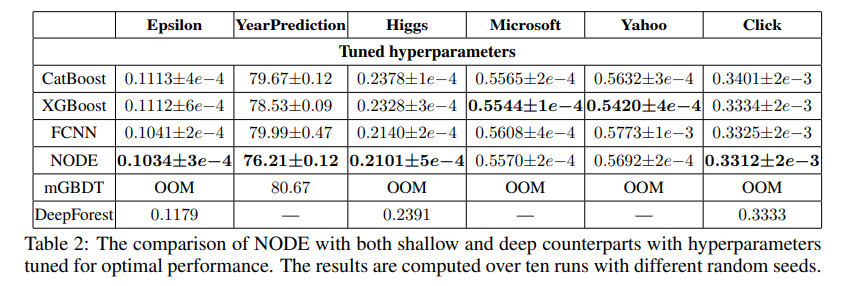
1. 기본 하이퍼파라미터를 사용할 경우 NODE는 모든 데이터셋에서 최고의 성능을 보여줌.
2. 튜닝된 하이퍼파라미터를 사용할 경우 NODE는 대부분의 작업에서 최고의 성능을 보여줌. Yahoo, Microsoft 데이터셋에서는 튜닝된 XGBoost가 가장 좋은 성능을 보여줌. Yahoo 데이터셋에서의 XGBoost의 이점을 감안하면, 이 데이터셋에 대해 ODTs를 사용하는 것이 부적절한 귀납적 편향이라고 추측할 수 있음.
3. 튜닝된 하이퍼파라미터를 사용하는 경우에서, FCNN은 일부 데이터셋에서 GBDT보다 성능이 뛰어났으나 다른 데이터셋에서는 GBDT가 FCNN 보다 우수하였음. 한편, NODE는 대부분의 가장 높은 성능을 제공하는 범용적인 도구로 보여짐.

추가로, 정형 데이터를 위한 기존의 딥러닝 아키텍처와 비교하였음. 소스 코드가 공개되어 있는 mGBDT, DeepForest(only in classification)를 사용하였으나, 메모리 부족 오류(OOM)가 발생하거나 GBDT 보다 성능이 낮았음.

ABLATIVE ANALYSIS

이번 섹션에서는 모델을 정의하는 주요 아키텍처 구성 요소를 분석함.

Choice functions

분할 특성 선택과 결정 트리 라우팅에 사용되는 choice function을 바꾸어 가며 성능을 평가함. 다음의 4가지 옵션을 실험하였음.

Softmax
모든 항목이 0이 아닌 가중치를 갖는 dense decision rules를 학습

Gumbel-Softmax
단일 요소를 확률적으로 샘플링하는 방법을 학습

Sparsemax
소수의 항목만 0이 아닌 가중치를 갖는 sparse decision rules를 학습

Entmax
sparsemax와 softmax의 일반화. sparse decision rules를 학습할 수 있으나 sparsemax보다 smoother하여 gradient 기반 최적화의 적절함.

Choice function에 따른 실험 결과는 다음과 같음.

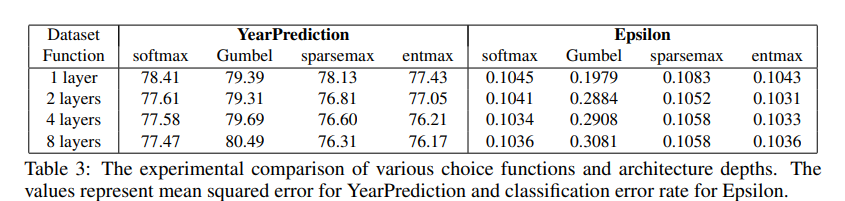
실험 결과, $\alpha=1.5$일 때의 entmax가 모든 실험에서 가장 뛰어난 성능을 보여주었음. sparsemax와 softmax는 보편적으로 우수한 성능을 보여주지 않았고, Gumbel-softmax는 딥러닝 아키텍처에 적절하지 않은 모습을 보여주었음.

Feature importance

이번 실험에서는 NODE에 의해 학습된 internal representations를 분석함. permutation test(feature importance)를 통해 여러 layer에서의 특성 중요도를 추정하였음.

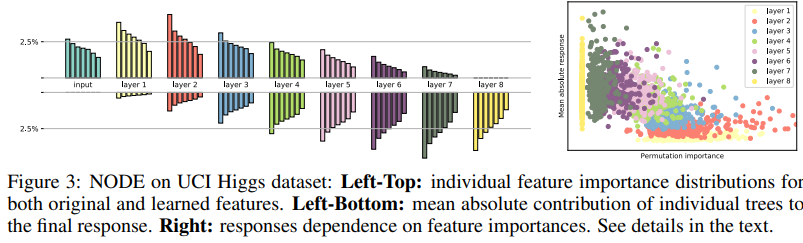
Higgs 데이터셋의 10,000개의 객체에 대해 각 특성의 값을 무작위로 섞어 분류 오류의 증가를 계산함. 그런 다음 각 layer에 대해 특성 중요도 값을 7개의 동일한 구간으로 나누고 각 구간의 특성 중요도 합을 계산함.

이를 통해, 첫 번째 layer의 특성이 가장 많이 사용되며 깊이가 깊어질수록 특성 중요도가 감소하는 것을 발견하였음. 이것은 deep layer가 중요한 특성을 생성할 수 있음을 의미함.

다음으로 최종 response에 대한 개별 트리의 mean absolute contribution을 추정하였고, deep trees가 최종 response에 더 많이 기여한다는 reverse trend를 확인할 수 있음.

오른쪽 산점도를 통해 최종 response에서 특성 중요도와 기여도 간 반비례 관계가 있음을 확인할 수 있음. 이것은 ealier layer의 역할은 informative features를 생성하는 것이고, latter layer의 역할은 정확한 예측을 위해 informative features를 사용하는 것임을 의미함.

Training/Inference runtime

마지막으로, NODE와 GBDT의 훈련 및 추론 시간을 비교함. 이 실험에서는 다른 모든 파라미터를 기본값으로 설정한 상태에서 깊이 6의 1,024개 트리로 구성된 앙상블을 평가함.

전반적으로, NODE의 추론 시간은 순수 PyTorch로 구현되었음에도 불구하고 최적화된 GBDT 라이브러리와 동등한 수준을 보임.

CONCLUSION

본 논문을 통해 정형 데이터를 위한 새로운 DNN 아키텍처를 제안함. 이 아키텍처는 역전파를 통해 end-to-end로 학습된 미분 가능한 deep GBDT 구조임. 광범위한 실험을 통해, 이 아키텍처의 장점을 입증하였음.

다음 연구 방향은 역전파를 통해 학습된 복잡한 파이프라인에 NODE layer를 통합하는 것임. 예를 들어, multi-modal 문제에서 이미지에 CNN을 사용하거나 시퀀스에 RNN을 사용하는 것처럼 정형 데이터를 통합하는 방법으로 NODE layer를 사용할 수 있을 것임.