[C++/MFC] 엣지검출 - 캐니 검출

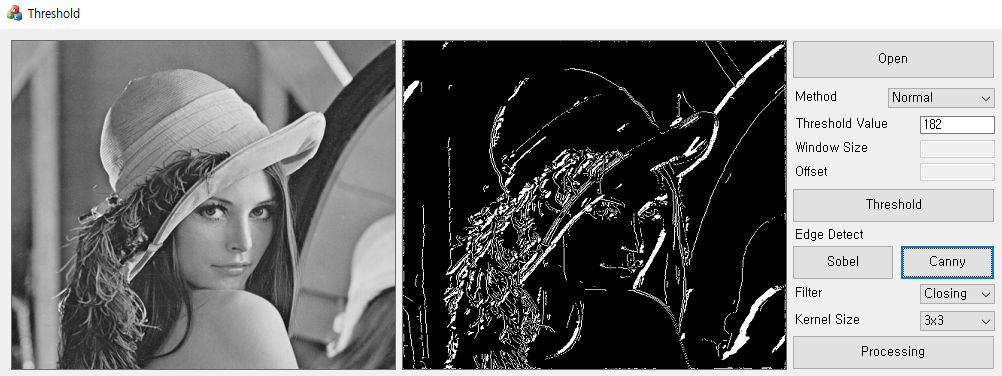
캐니 엣지는 윤곽을 잘 찾아내면서도, 원래 영상들의 노이즈를 제거하는데도 유용한 엣지검출 방법이다. 이미지를 대상으로 소벨 검출과 캐니 검출을 둘 다 시행했을 때 캐니 검출이 보다 블롭을 찾아내기 쉬웠다.

하지만 소벨 검출에 비해서는 과정이 많이 복잡하고 시간이 오래걸려 구현이 쉽지는 않았다.

캐니 검출은 다음과 같은 과정을 통해 진행된다.

1. 가우시안 필터링 진행

우선 이미지의 노이즈를 제거하고 블러처리하는 작업이 필요하다. 이를 위해서는 메디안 필터를 사용하거나, 보편적으로 가우시안 함수를 적용한다. 우린 이전에 가우시안 필터링을 구현했으니 이를 이용해본다.

float gaussianKernel[5][5] = {
	{1 / 273.0f, 4 / 273.0f, 7 / 273.0f, 4 / 273.0f, 1 / 273.0f},
	{4 / 273.0f, 16 / 273.0f, 26 / 273.0f, 16 / 273.0f, 4 / 273.0f},
	{7 / 273.0f, 26 / 273.0f, 41 / 273.0f, 26 / 273.0f, 7 / 273.0f},
	{4 / 273.0f, 16 / 273.0f, 26 / 273.0f, 16 / 273.0f, 4 / 273.0f},
	{1 / 273.0f, 4 / 273.0f, 7 / 273.0f, 4 / 273.0f, 1 / 273.0f}
};

void GaussianFilter(BYTE* src, BYTE* dst, int width, int height, float sigma)
{
	int size = 5; // 가우시안 커널 크기
	int half = size / 2;
	float sum = 0.0f; // 커널의 합을 저장

	// 가우시안 커널 생성
	float** kernel = new float*[size];
	for (int i = 0; i < size; i++) {
		kernel[i] = new float[size];
	}

	// 가우시안 커널 계산
	for (int i = -half; i <= half; i++) {
		for (int j = -half; j <= half; j++) {
			kernel[i + half][j + half] = exp(-(i * i + j * j) / (2 * sigma * sigma)) / (2 * 3.141592653589793238 * sigma * sigma);
			sum += kernel[i + half][j + half];
		}
	}

	// 가우시안 커널 정규화
	for (int i = 0; i < size; i++) {
		for (int j = 0; j < size; j++) {
			kernel[i][j] /= sum;
		}
	}

	// 가우시안 블러 적용
	for (int y = half; y < height - half; y++) {
		for (int x = half; x < width - half; x++) {
			float pixel = 0.0f;

			for (int i = -half; i <= half; i++) {
				for (int j = -half; j <= half; j++) {
					pixel += src[(y + i) * width + (x + j)] * kernel[i + half][j + half];
				}
			}

			dst[y * width + x] = (BYTE)pixel;
		}
	}

	// 메모리 해제
	for (int i = 0; i < size; i++) {
		delete[] kernel[i];
	}
	delete[] kernel;
}

2. 그래디언트 계산

다음은 미분 값을 통해 경사를 찾고, 엣지를 검출한다.
즉, 원래 이미지를 미분하여 Image의 강도가 급격히 변하는 부분을 찾아낸다.
그를 위해서는 경사의 방향과 크기를 찾아내야한다.

우선 크기는 다음과 같다.

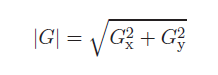
이를 코드로 구현하면 다음과 같다.

for (int i = -1; i <= 1; i++) {
				for (int j = -1; j <= 1; j++) {
					dx += src[(y + i) * width + (x + j)] * Gx[i + 1][j + 1];
					dy += src[(y + i) * width + (x + j)] * Gy[i + 1][j + 1];
				}
			}

			// 그래디언트 크기 계산 -> root(x^2 + y^2)
			grad[y * width + x] = (BYTE)sqrt(dx * dx + dy * dy);
               

이후에 경사의 방향은 아크탄젠트를 통해 세타값을 얻을 수 있다.

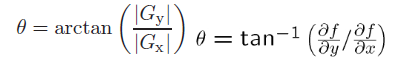
// 그래디언트 방향 계산
			if (dx == 0) { // 수직 방향
				theta[y * width + x] = 90;
			}
			else {
				theta[y * width + x] = (BYTE)atan2(dy, dx) * 180 / 3.141592653589793238;
			}

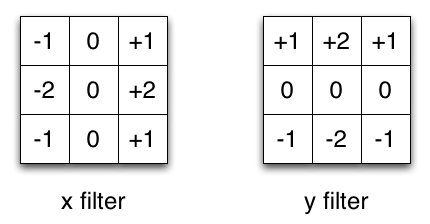
이렇게 그래디언트를 계산하기 위해서 이전에 만든 소벨 연산자를 활용했다.

void ComputeGradient(BYTE* src, BYTE* grad, BYTE* theta, int width, int height)
{
	int Gx[3][3] = { {-1, 0, 1}, {-2, 0, 2}, {-1, 0, 1} }; // 소벨 연산자 (수평)
	int Gy[3][3] = { {-1, -2, -1}, {0, 0, 0}, {1, 2, 1} }; // 소벨 연산자 (수직)

	for (int y = 1; y < height - 1; y++) {
		for (int x = 1; x < width - 1; x++) {
			int dx = 0, dy = 0;

			// 소벨 연산자 적용
			for (int i = -1; i <= 1; i++) {
				for (int j = -1; j <= 1; j++) {
					dx += src[(y + i) * width + (x + j)] * Gx[i + 1][j + 1];
					dy += src[(y + i) * width + (x + j)] * Gy[i + 1][j + 1];
				}
			}

			// 그래디언트 크기 계산 -> root(x^2 + y^2)
			grad[y * width + x] = (BYTE)sqrt(dx * dx + dy * dy);

			// 그래디언트 방향 계산
			if (dx == 0) { // 수직 방향
				theta[y * width + x] = 90;
			}
			else {
				theta[y * width + x] = (BYTE)atan2(dy, dx) * 180 / 3.141592653589793238;
			}
		}
	}
}

3. Non-maximum Suppression

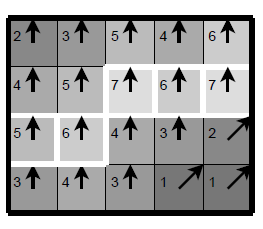
다음은 극값을 선택해야한다. 즉, Edge가 아님에도 검출되는 영역이 없도록 잘못된 노이즈를 제거하는 작업이 필요하다.

void NonMaximumSuppression(BYTE* grad, BYTE* theta, BYTE* nms, int width, int height)
{
	// grad 배열을 복사해서 nms 배열 초기화
	memcpy(nms, grad, width * height * sizeof(BYTE));

	for (int y = 1; y < height - 1; y++) {
		for (int x = 1; x < width - 1; x++) {
			int dir = theta[y * width + x] / 45; // 그래디언트 방향 (4방향)

			// 그래디언트 방향에 따른 비 최대 억제
			switch (dir) {
			case 0: // 수평 방향
				if (grad[y * width + x] <= grad[y * width + x - 1] || grad[y * width + x] <= grad[y * width + x + 1]) {
					nms[y * width + x] = 0;
				}
				break;
			case 1: // 대각선 방향 (/)
				if (grad[y * width + x] <= grad[(y - 1) * width + x + 1] || grad[y * width + x] <= grad[(y + 1) * width + x - 1]) {
					nms[y * width + x] = 0;
				}
				break;
			case 2: // 수직 방향
				if (grad[y * width + x] <= grad[(y - 1) * width + x] || grad[y * width + x] <= grad[(y + 1) * width + x]) {
					nms[y * width + x] = 0;
				}
				break;
			case 3: // 대각선 방향 (\)
				if (grad[y * width + x] <= grad[(y - 1) * width + x - 1] || grad[y * width + x] <= grad[(y + 1) * width + x + 1]) {
					nms[y * width + x] = 0;
				}
				break;
			}
		}
	}
}

4. Double Thresholding

이제 마지막으로 남아있는 일부 잡음(noise)을 잡아내기 위해 임계값을 사용한다.

그를 위해서는 강한 엣지와 약한 엣지로 두 부분을 나누어서 잡아낸다.

for (int y = 0; y < height; y++) {
		for (int x = 0; x < width; x++) {
			// 강한 가장자리
			if (nms[y * width + x] >= upper) {
				edge[y * width + x] = 255;
			}
			// 약한 가장자리
			else if (nms[y * width + x] >= lower) {
				edge[y * width + x] = 128;
			}
			// 비 가장자리
			else {
				edge[y * width + x] = 0;
			}
		}
	}

즉, 이미지의 하얗게 진한 영역은 강한 엣지, 옅은 회색 영역은 약한 엣지이고 이 약한 엣지만 최종적으로 판별할 수 있으면 된다.

for (int y = 1; y < height - 1; y++) {
		for (int x = 1; x < width - 1; x++) {
			// 약한 가장자리
			if (edge[y * width + x] == 128) {
				// 주변에 강한 가장자리가 있는지 확인
				if (edge[(y - 1) * width + x - 1] == 255 || edge[(y - 1) * width + x] == 255 || edge[(y - 1) * width + x + 1] == 255 ||
					edge[y * width + x - 1] == 255 || edge[y * width + x + 1] == 255 ||
					edge[(y + 1) * width + x - 1] == 255 || edge[(y + 1) * width + x] == 255 || edge[(y + 1) * width + x + 1] == 255) {
					edge[y * width + x] = 255; // 강한 가장자리로 판정
				}
				else {
					edge[y * width + x] = 0; // 비 가장자리로 판정
				}
			}
		}
	}

이제는 강한 엣지를 포함하는 Blob은 보존하고, 그 외의 부분은 날려버리는 작업을 하면 된다.
최종적으로 필터링이 끝난 이미지는 Sobel과 비교해서 유의미한 차이를 보인다.

본 게시물은 https://carstart.tistory.com/188를 참고했습니다.