Interpolation (내삽)
Interpolation(내삽)은 2점 사이에 있는 점의 값을 구하는 방법이다.

3,5 사이에 점 4가 있다.
이 경우 4는 3,5 정 중앙에 있기 때문에 평균을 내면 바로 구하는게 가능하다.
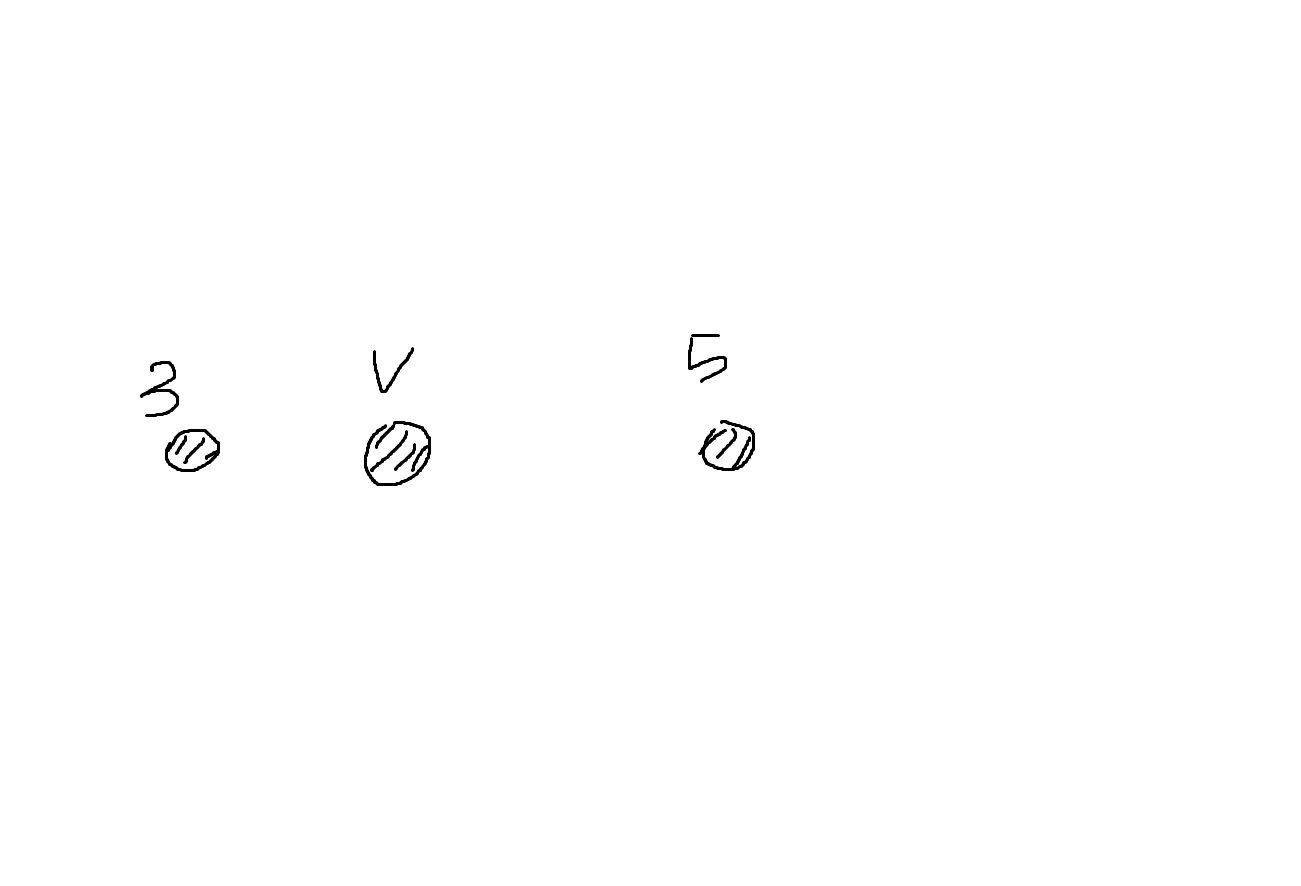
중앙에 있지 않는 점 V의 값은 어떻게 구할까?
V의 값은 내삽을 이용하여 구한다.
내삽의 아이디어는 다음과 같다.
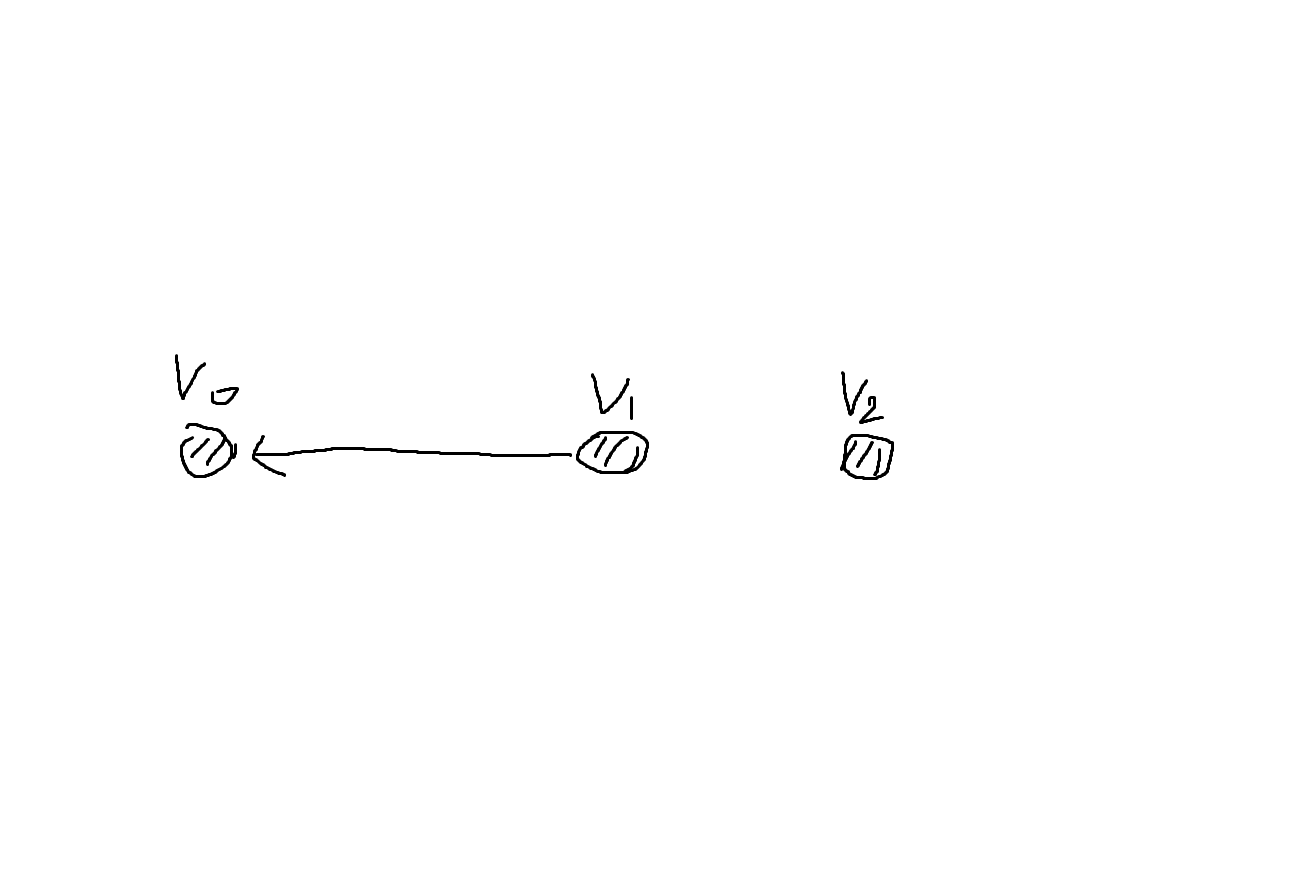
점 V1은 V0와 멀수록 v2에 가깝다.
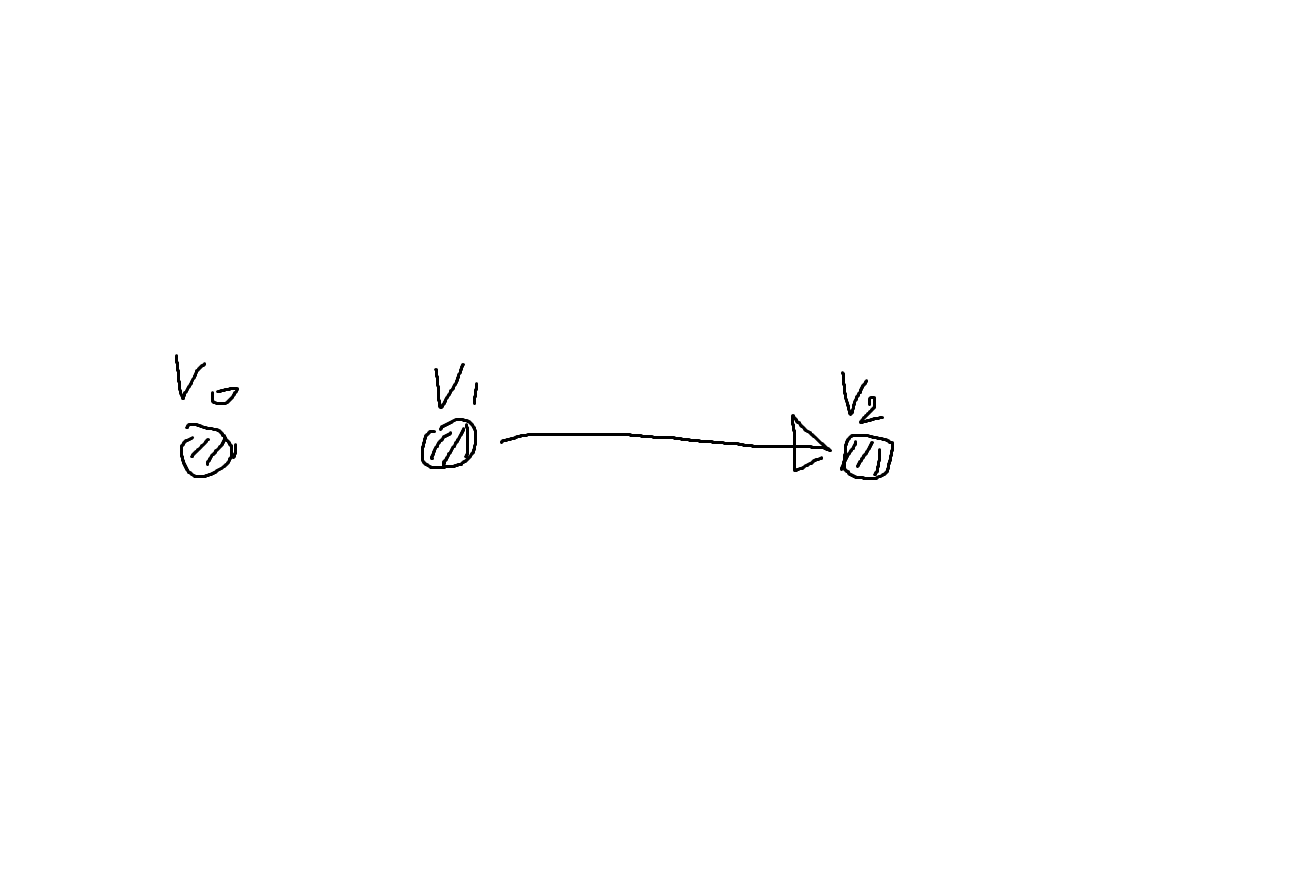
V2와 거리가 멀수록 V1에 가깝다.
이걸 관계식으로 구성하면 다음과 같다.
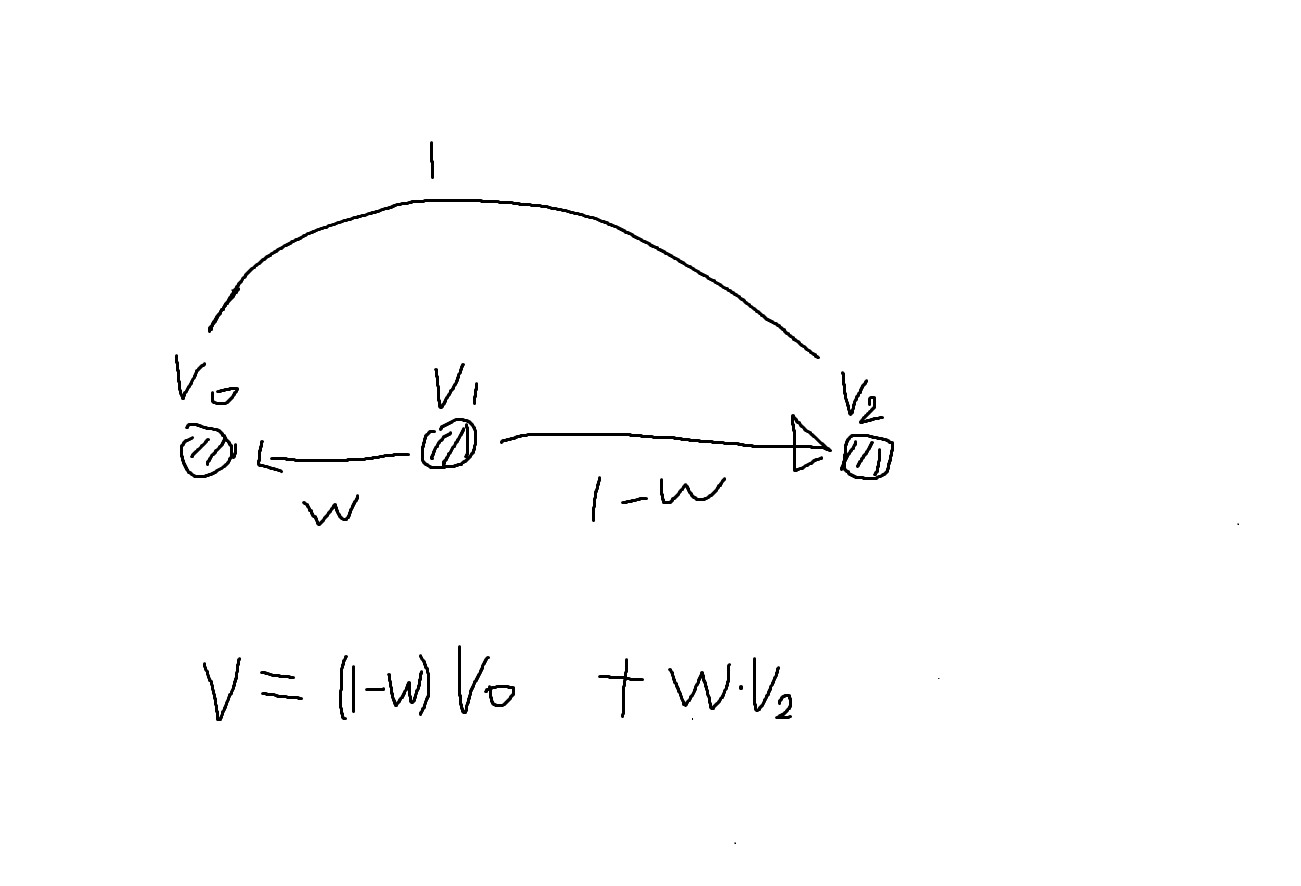
V1이 V2에 가까워질수록 w 가중치가 높아진다.
반대로 V1이 V0에 가까워질수록 1-W 가중치가 높아진다.
이를 식으로 공식으로 세우면 보간법이 된다.
Barycentric coordinate (무게 중심 좌표계)
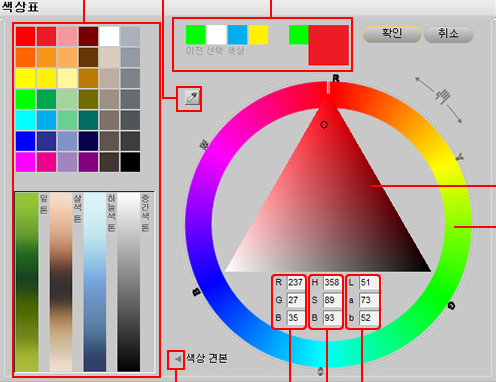
프론트 개발을 하다보면 위처럼 생긴 삼각형 색상 좌표계를 본적이 있다. 이건 무게중심 좌표계를 사용하여 만들 수 있다.
무게중심 좌표계는 나중에 텍스처링을 공부할때 사용되고 내삽을 이용하여 구현한다.
어떻게 내삽을 이용하여 저런 삼각형 좌표계를 만들 수 있는지 설명하겠다.
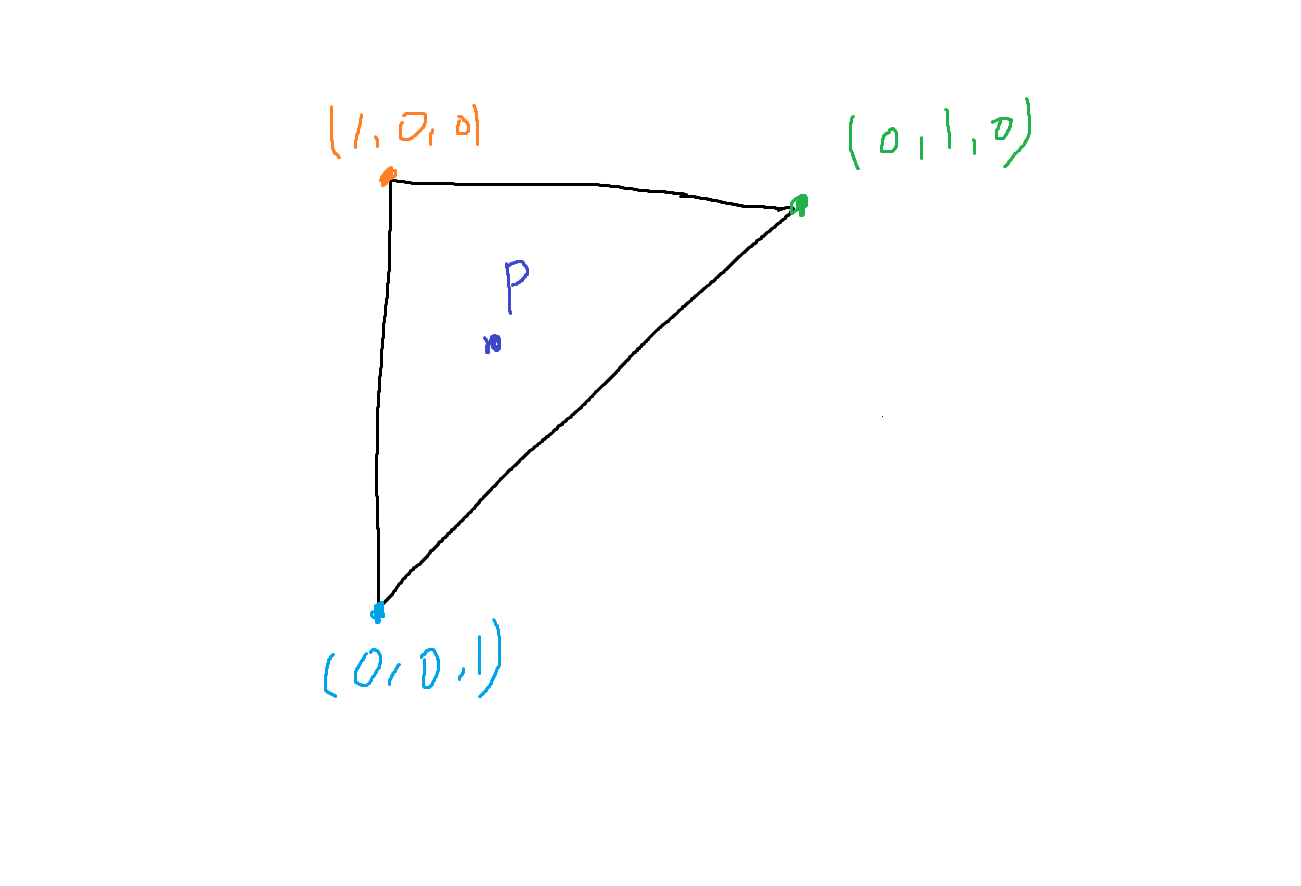
삼각형의 각 끝을 RGB 좌표계로 보고 접근하자.
여기서 점 P를 구하면 된다.
P와 각 끝점을 이어보자.
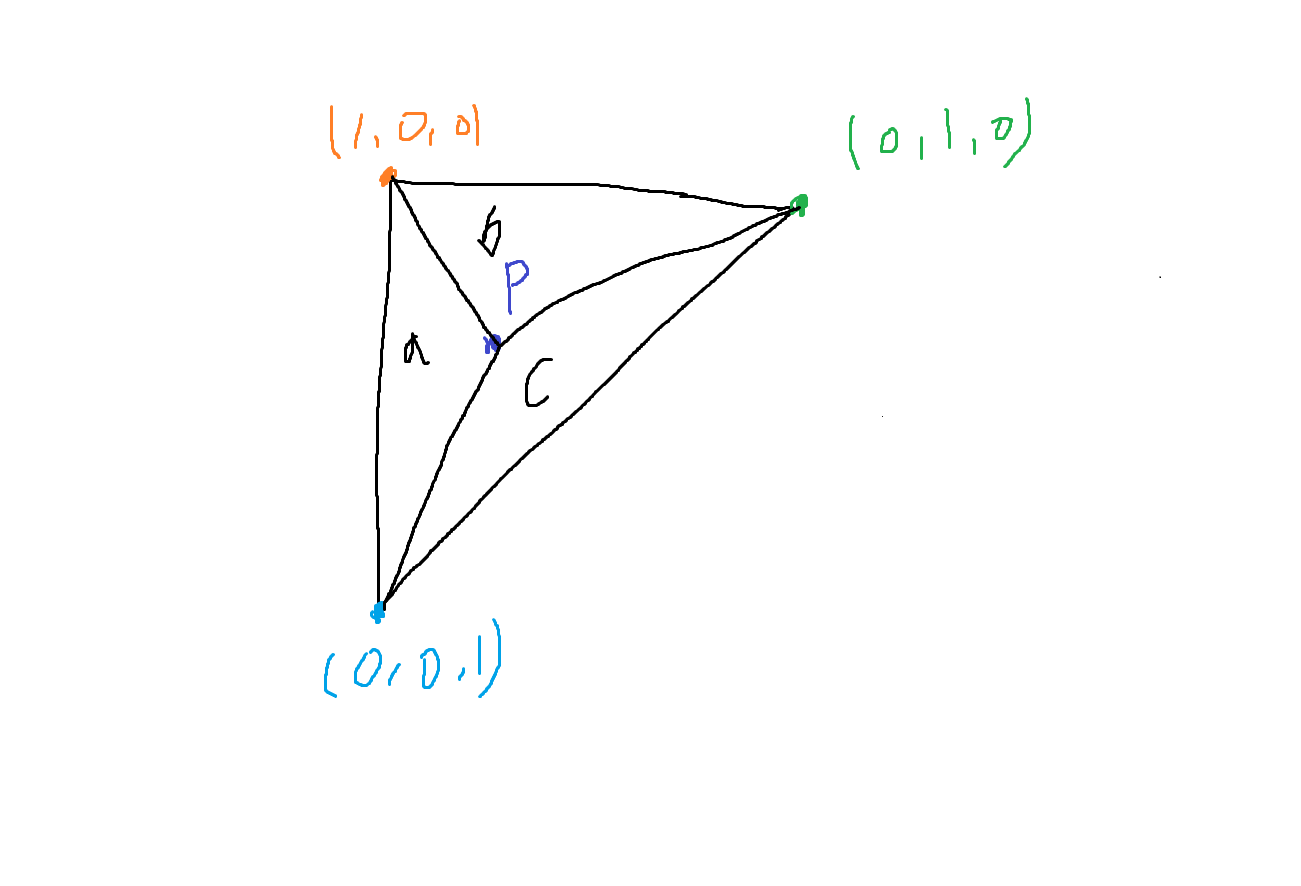
각 끝점을 이으면 3개의 삼각형 (a,b,c)가 생긴다.
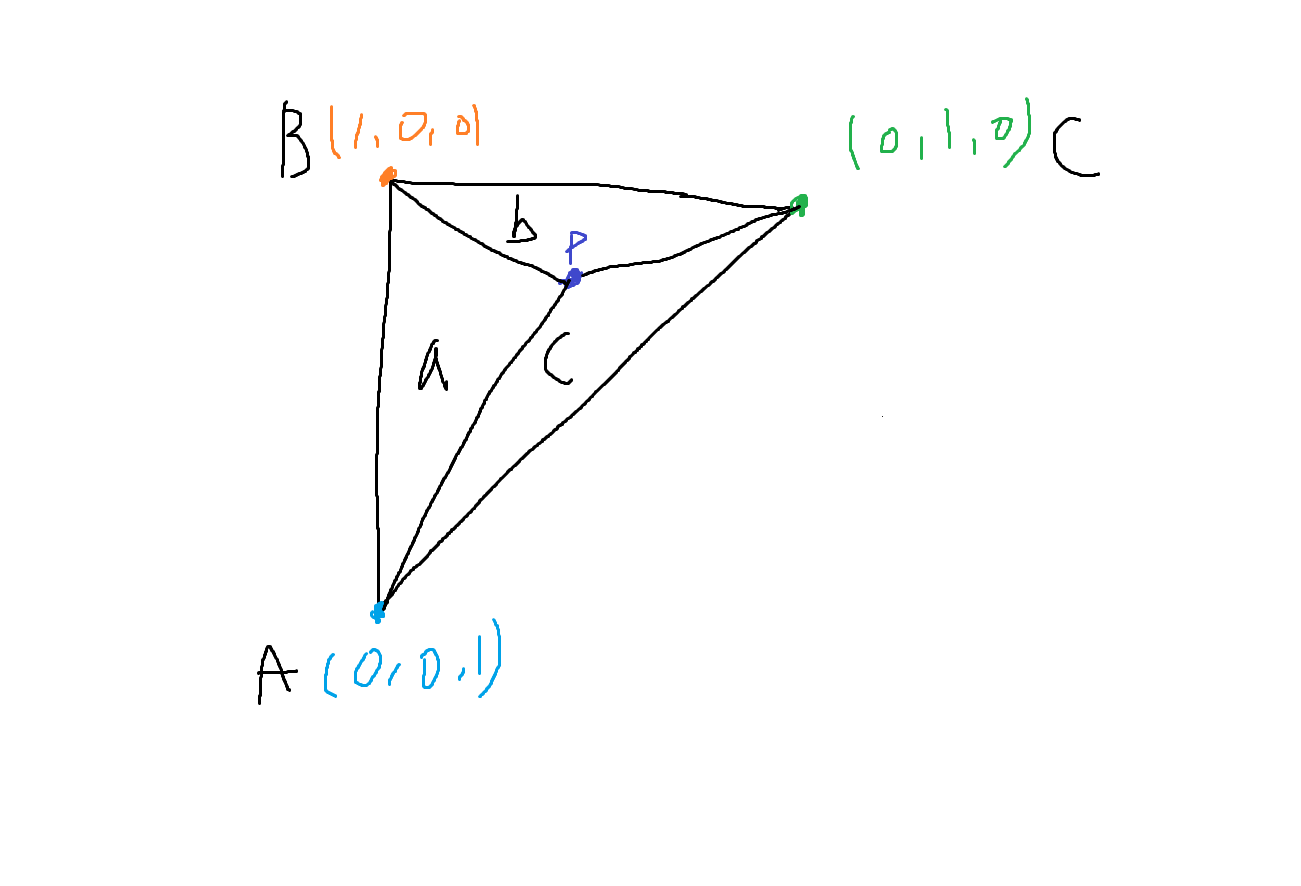
점 P는 벡터 C에 가까워질수록 a 삼각형의 넓이가 커진다.
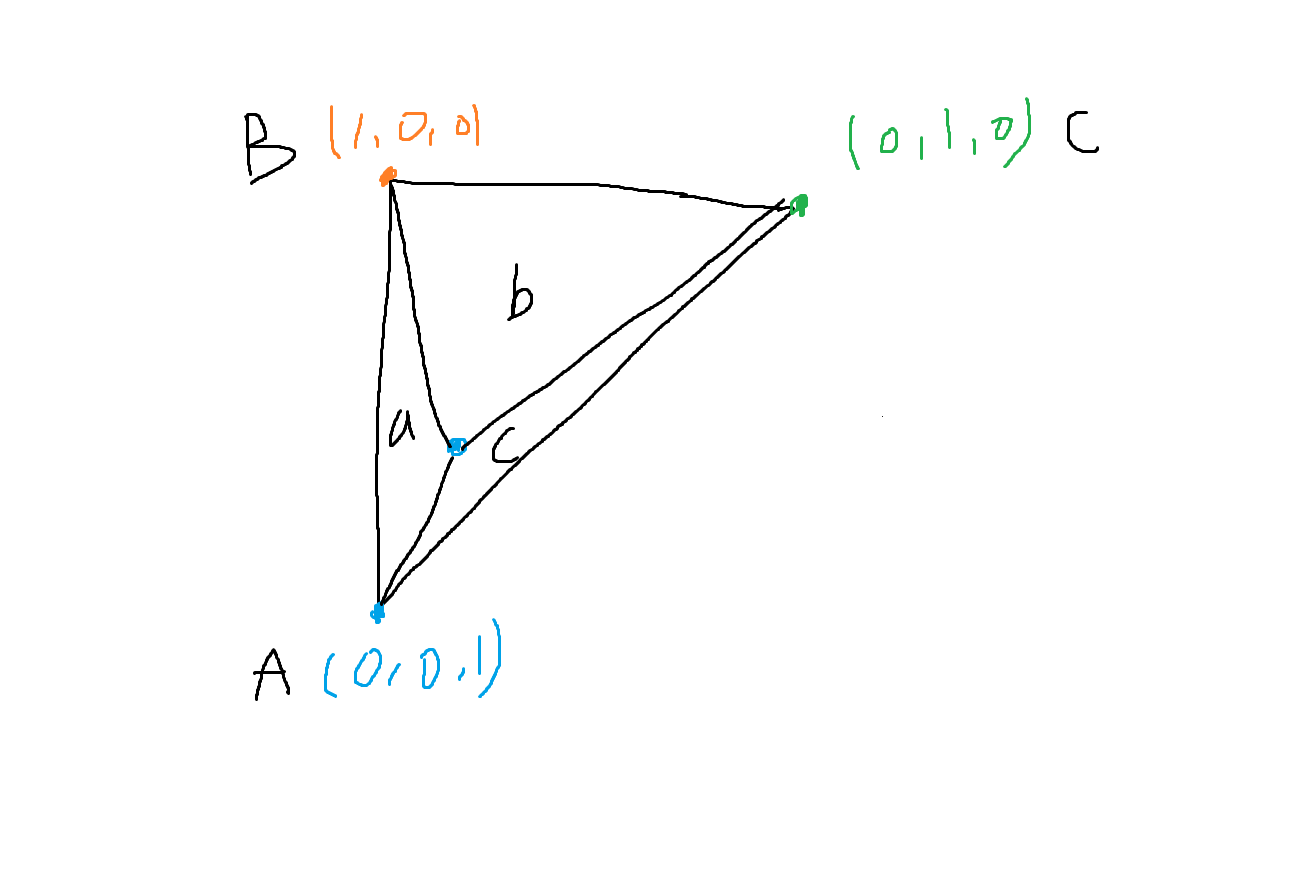
점 P가 벡터 A에 가까워 질수록 b 삼각형의 넓이가 커진다.
마찬가지로 P가 B에 가까워질수록 c 삼각형의 넓이가 커진다.
이제 이를 바탕으로 관계식을 짜보면 다음과 같다.
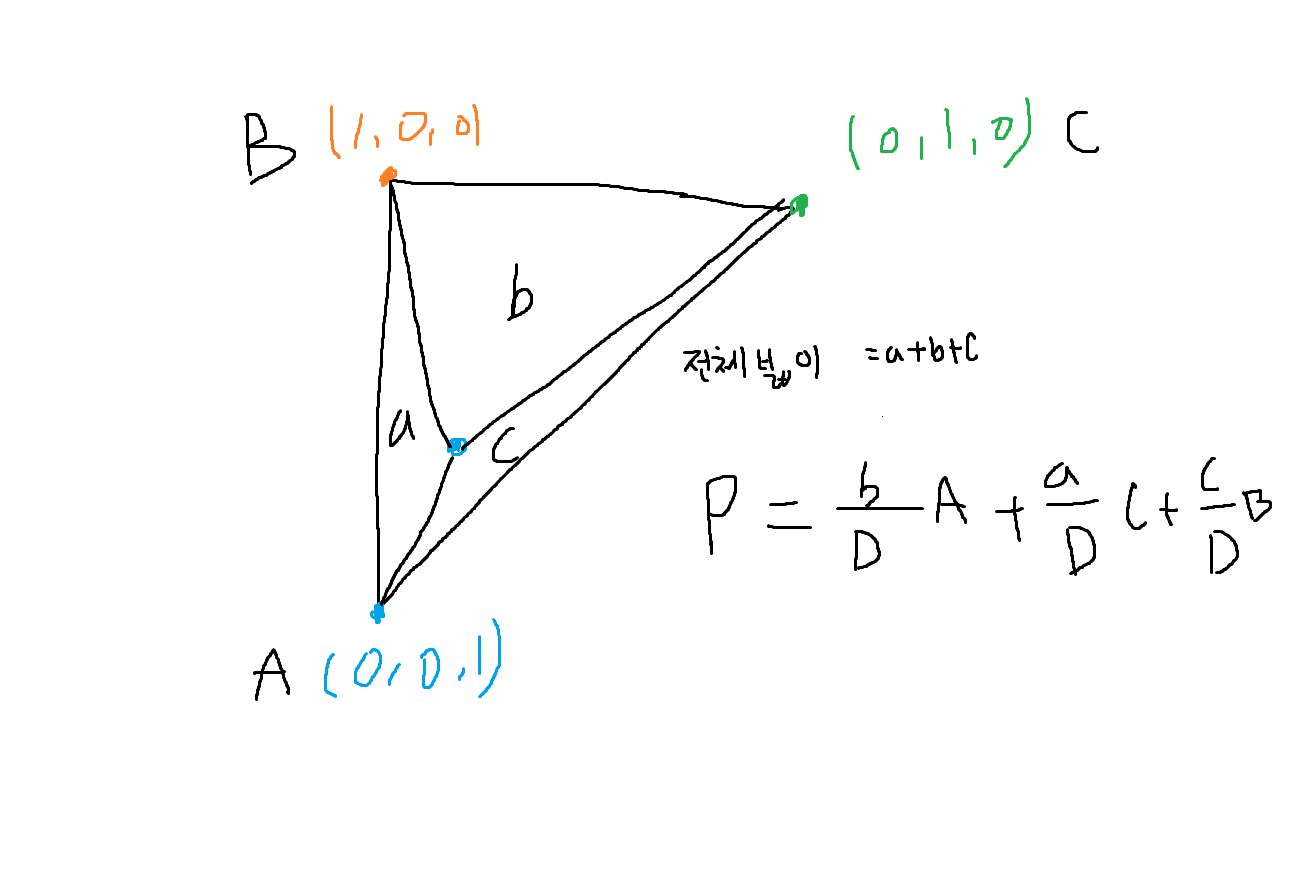
삼각형 a,b,c는 벡터 외적을 통해 구하는게 가능하다.
또한 벡터 * 스칼라 = 벡터 이기 때문에 벡터의 값이 나와 P 의 위치를 구하는것이 가능하다.
