https://honglab.co.kr/ 그래픽스 파트를 읽고 중요한 개념들을 정리하는 글입니다.
레이트레이싱의 기본 틀은 다음과 같다.
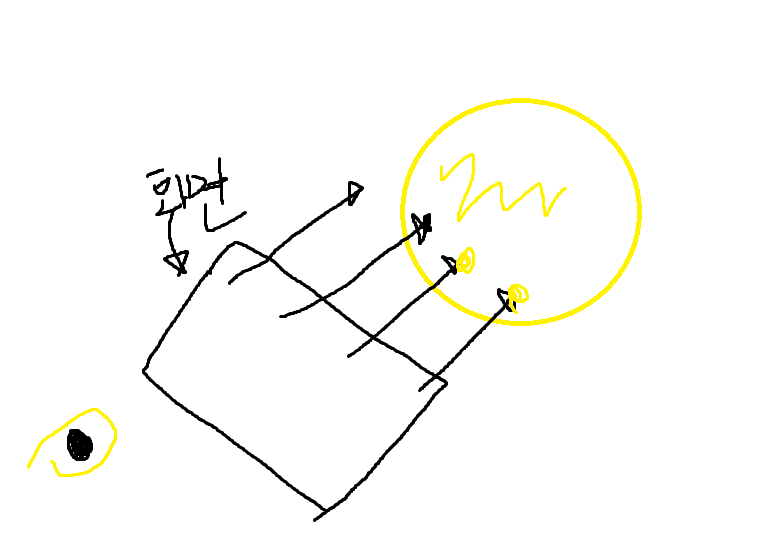
컴퓨터속에 3D 물체가 있고, 그리고자 하는 화면의 각 픽셀에서 Ray (광선을) 쏴 3D 물체에 맞는지 확인하고 물체에 충돌했다면 물체의 색상을 픽셀에 그리는 구조로 돌아간다.
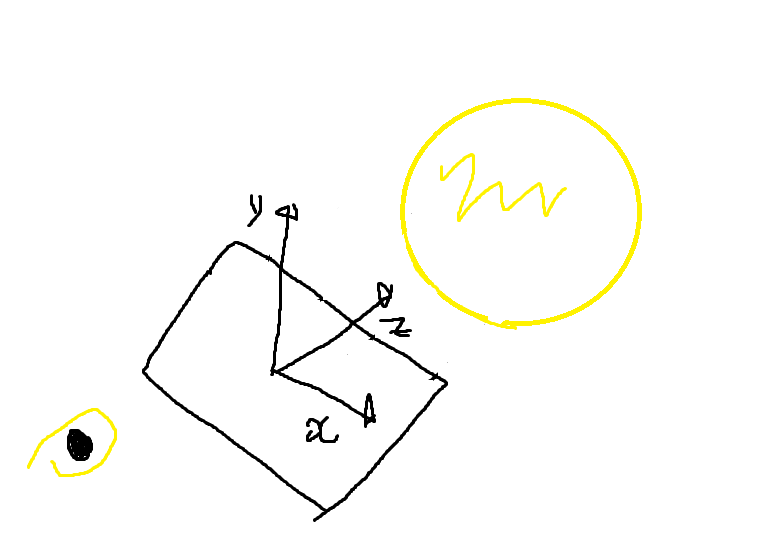
이때 화면은 X,Y 축이고 물체와 떨어진 거리는 Z 로 표현할 수 있다.
이때 Ray의 방향은 Z의 방향이고 (0,0,1) 로 표현이가능하다.
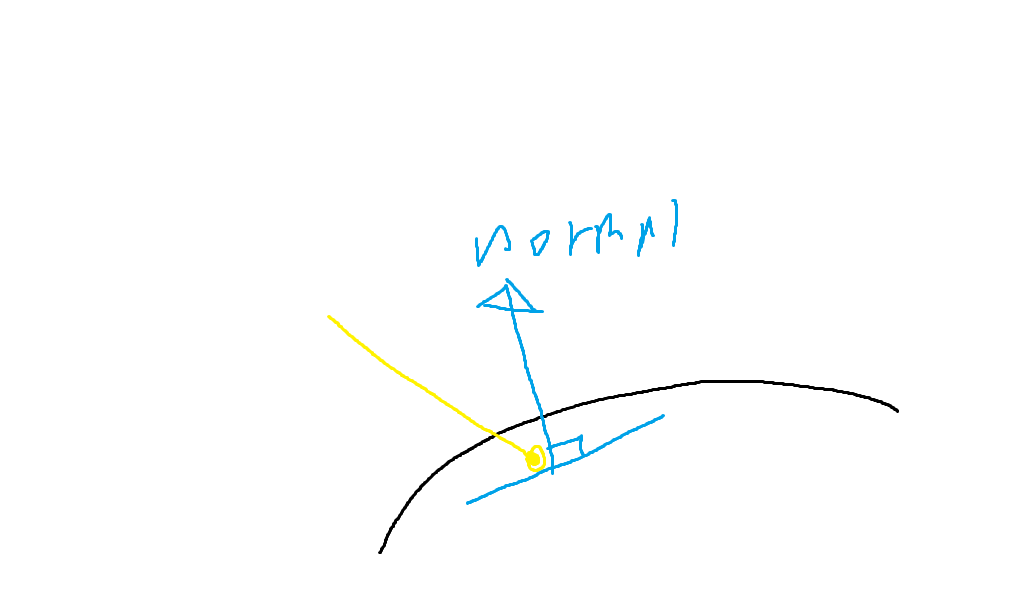
이때 구와 충돌한 점에서, 충돌한 지점에서 수직으로 나가는 법선벡터를 normal 벡터라고 부른다.
구의 경우 단순히 충돌지점 P와 구의 중심 C 에서 P-C가 normal 벡터가 된다.
구의 충돌 공식은 다음 위키 피디아에서 확인할 수 있다.
https://en.wikipedia.org/wiki/Line%E2%80%93sphere_intersection
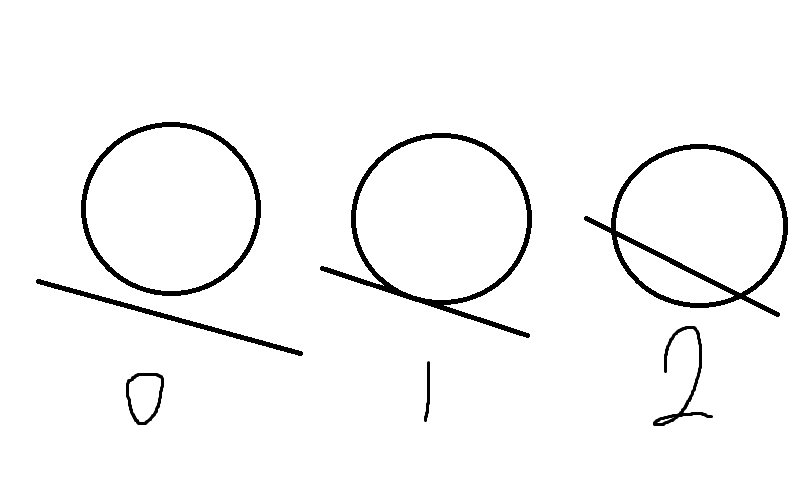
어떤 한 직선이 구와 만나는 케이스는 3가지가 있다.
- 완전히 빗겨나가서 충돌하지 않는다.
- 접선으로 구의 표면중 1개와 부딪힌다.
- 구를 뚫고 2개의 표면과 부딪힌다.
구와 충돌하는 케이스는 2,3 이고 위키피디아에서 공식을 통해서 값을 구하면 된다.

구의 공식은 다음과 같다.

아래는 선 (Ray)의 공식이다.
선과 구가 만나는 케이스는 선의 공식 ( x = o + du ) 을 구의 공식에 대입하면 구할 수 있다.
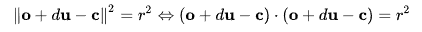
이를 대입한 공식이 위키피디아의 이 공식이다.
수식을 풀어서 정리하면 이렇게 다시 정리할 수 있다.
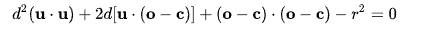
여기서 똑똑하신 분들이 이 공식을 근의 정리를 통해서 해결할 수 있음을 발견했다. 원점에서의 거리 d를 근의공식으로 푸는 공식은 아래와 같다.

(어질어질 ... 하다 )
사실 위의 공식들은 그다지 핵심 사항이 아니다.
구의 충돌을 구현하는데 중요한 수식은 위키피디아의 마지막에 정리되어져 있다.
근의공식으로 푼 수식중 이 부분이 나블라이다.

나블라가 ( 역삼각형 ) < 0 일땐 구에 충돌이 일어나지 않았고
>= 0 일 경우 충돌이 일어났다.
따라서 위 수식에서 나블라를 구하면 구의 충돌을 쉽게 판별할 수 있다.
재밋는 점은 d에서 나블라를 +- 연산을 하고 있다.
그렇기 때문에 d값은 d1,d2값 2개로 나온다. d1 d2를 그림으로 그리면 아래와 같다.
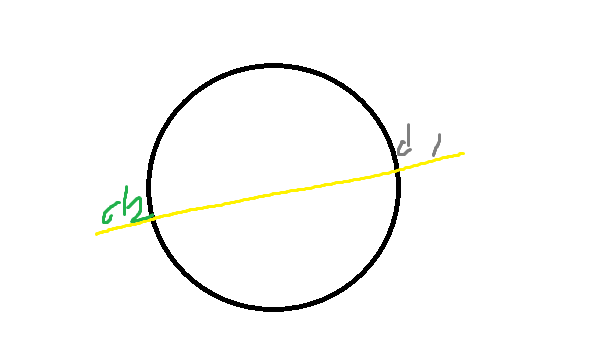
구와 충돌할때 점이 2개가 나오므로 d1,d2 2개의 값이 나오고 화면에선 앞 부분만 노출되기 때문에 d1,d2중 가까운 값(작은 값)을 사용하면 된다.
종종 d1,d2가 음수로 나오는 경우도 있는데 그 케이스는 아래와 같다.
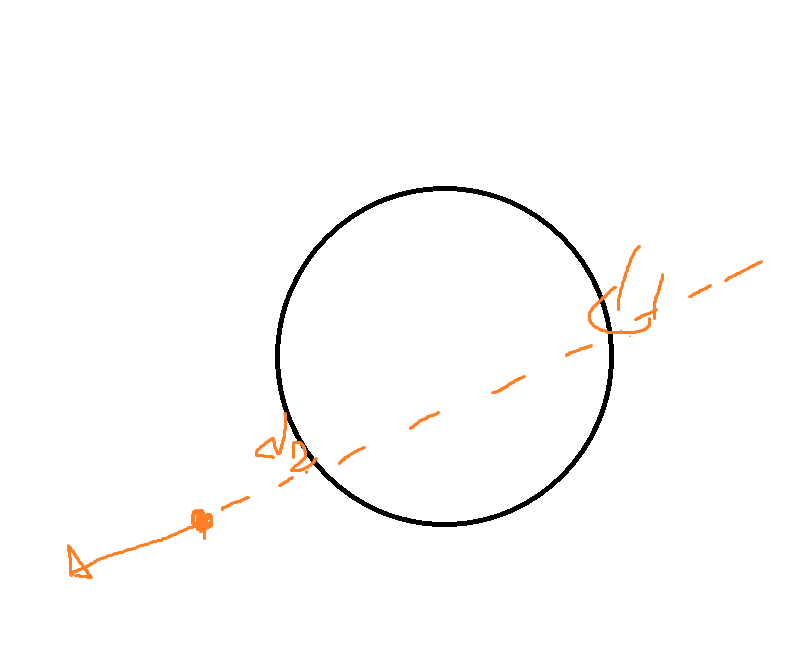
d1,d2 값이 화면 밖으로 나갔을 경우이다. 화면 밖에 나간 구는 그리지 않아야 함으로 음수값이 나올경우 렌더링 하지 않아야 한다.
