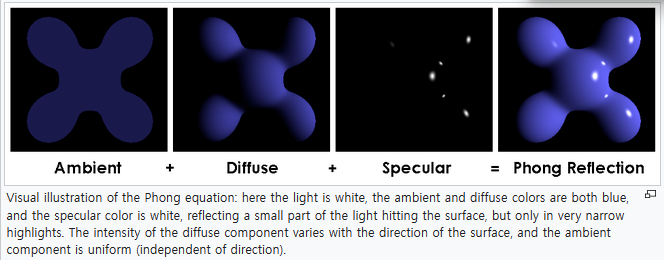
퐁 모델은 Ambient + Diffuse + Specular를 사용하여 물체를 그리는 방법이다.
Ambient
Ambient는 간접조명을 의미한다.
Ambient는 빛에 노출되지 않아도 다른 물체로부터 반사되어온 빛이기 때문에 광원과 관계없이 "모든" 사물의 면에 비추게 된다.
따라서 빛에 반사된 지점의 normal 벡터와 관계가 없이 독립적인 값으로 그린다.
Diffuse
Diffuse는 난반사를 의미한다.
반사를 표현함으로 인해서 3D 모델을 더 사실적이게 표현하게 된다.
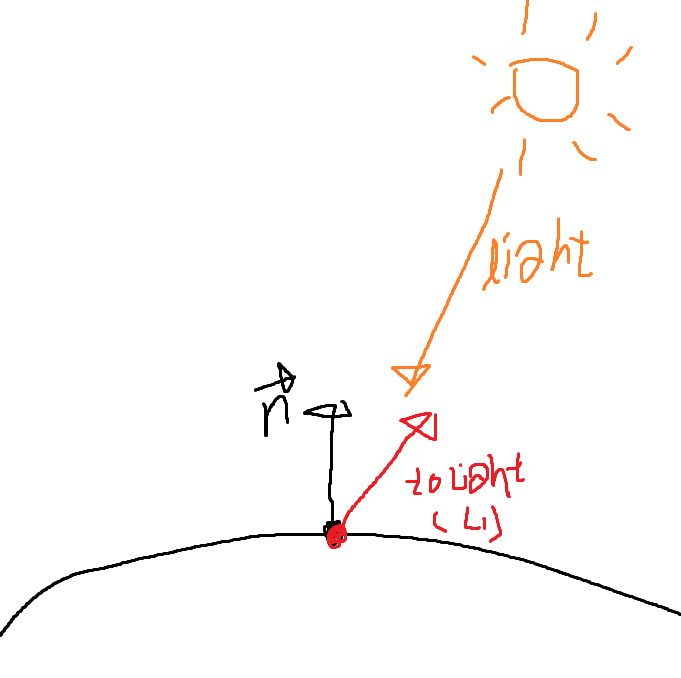
구에서의 Diffuse를 그림의로 보현하면 위 사진과 같다.
오른쪽 위에 광원이 있고 구 표면에 충돌했다.
n은 normal vector이고, toLight은 충돌한 구 표면에서 조명으로 향하는 L1 벡터이다.
Diffuse는 빛의 각도에 따른 표면의 밝기를 조절해야한다. 이는 벡터의 내적을 사용하여 구현할 수 있다.
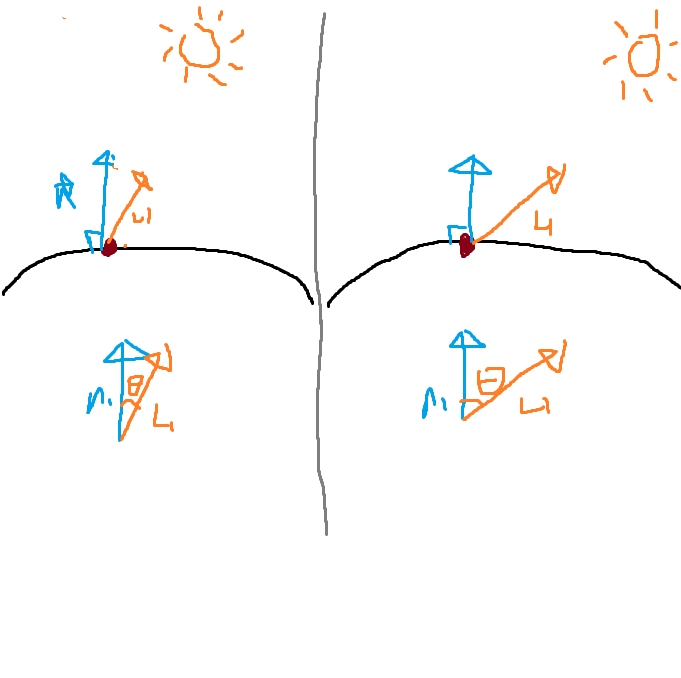
normal 벡터는 항상 표면과 수직이고 L1 벡터는 조명의 위치에 따라 달라진다.
조명이 수직에 가까울수록 normal 벡터와 L1 벡터의 사이 각도는 좁아지고
조명이 멀어질수록 각도는 넓어진다.
normal 벡터는 유닛 벡터이므로 n * l 내적을 구하여 값이 클수록 빛을 더 받고 있다는 의미이다.
이때 l 벡터도 normalize 하면 값의 크기가 1이 되고
내적의 값은 항상 cos(theta)가 된다.
따라서 n * l(normalize) = cos(theta)가 된다.
처리해야할 예외 케이스가 하나 있는데 조명이 반대편에 있을 경우이다.
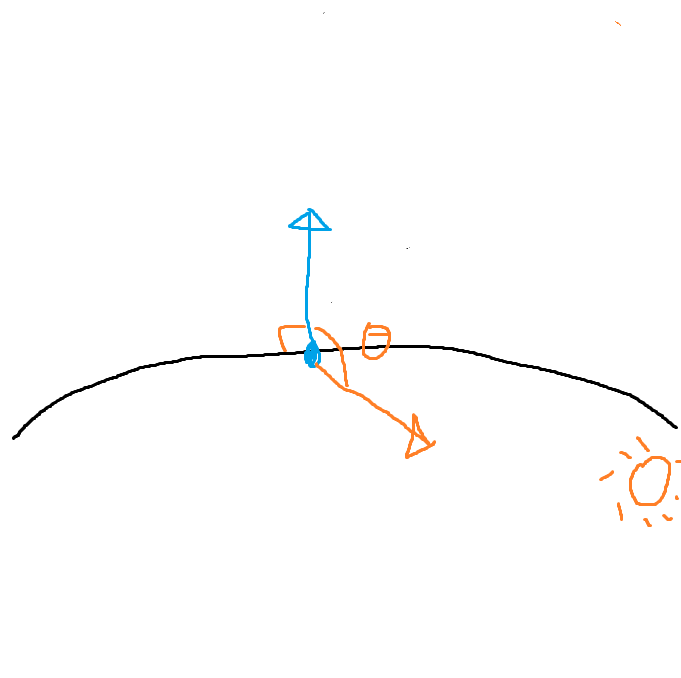
조명이 지구 반대편에 있을 경우 빛은 0이다.
하지만 cos은 90도가 넘는 경우에도 값이 있기 때문에 0.0f 보다 낮은 값이 안나오도록 처리해야한다.
max(n*l,0.0f)
Specular
Specular는 표면의 반짝임을 구현할때 사용한다.
현실 세계에서 반짝이는 부분은 빛이 반사되어 시야에 제대로 들어올때 반짝인다.
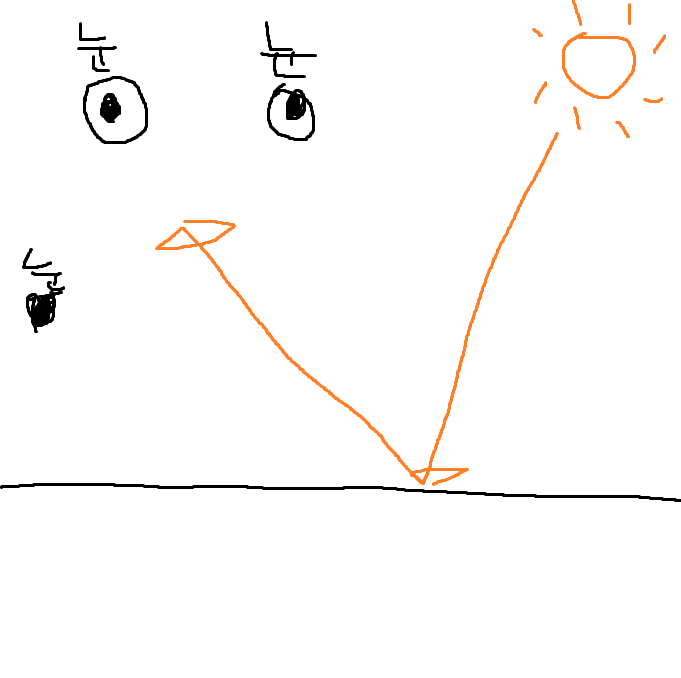
(그림처럼 정확히 눈에 들어와야한다.)
전반사가 되는 지점을 찾아야한다 이를 벡터로 표현하면 다음과 같다.
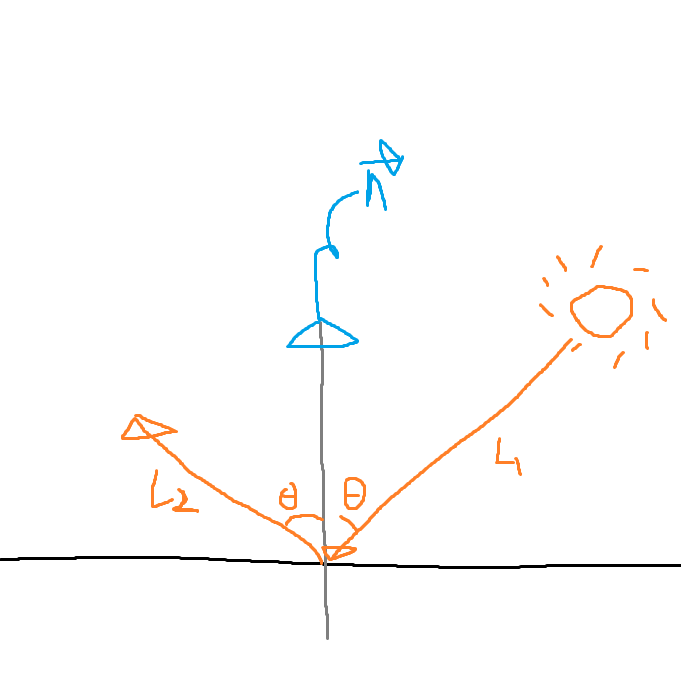
L2 벡터를 구해야하는데 전반사이기 때문에 같은 각도를 가지며 반사되고 있다.
L1을 회전 시켜 L2를 구할 수 있지만 다른 방법으로 벡터를 구하는 방법도 있다.
우선 L1을 n와 내적시켜 거리를 구한다.
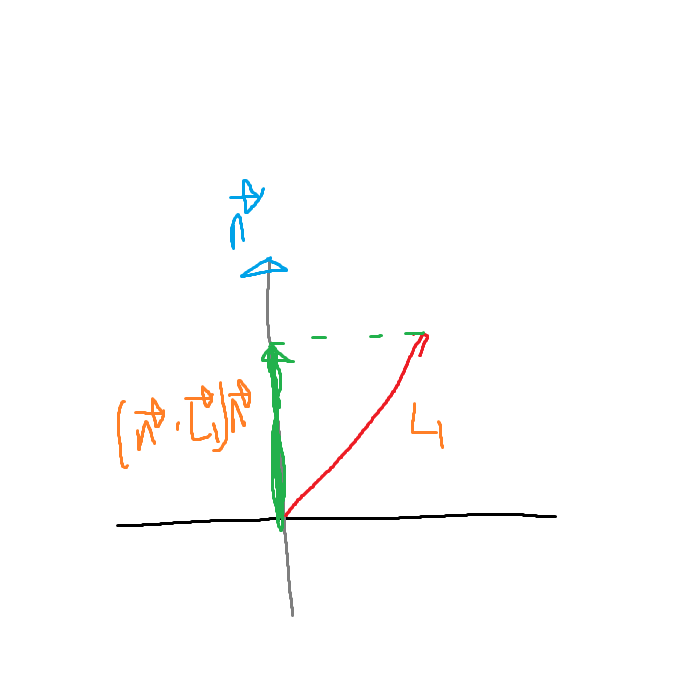
n 벡터는 유닛벡터이기 때문에 L1 * n 내적 시키면 거리량이 나온다. 이를 다시 유닛벡터로 곱하면, L1의 y축값만큼의 스칼라를 가지지만 n벡터 와 같은 방향인 벡터가 나온다. ( 벡터 S라고 부르겠다. )
이제 S에서 L을 향하는 벡터 A를 구한다.
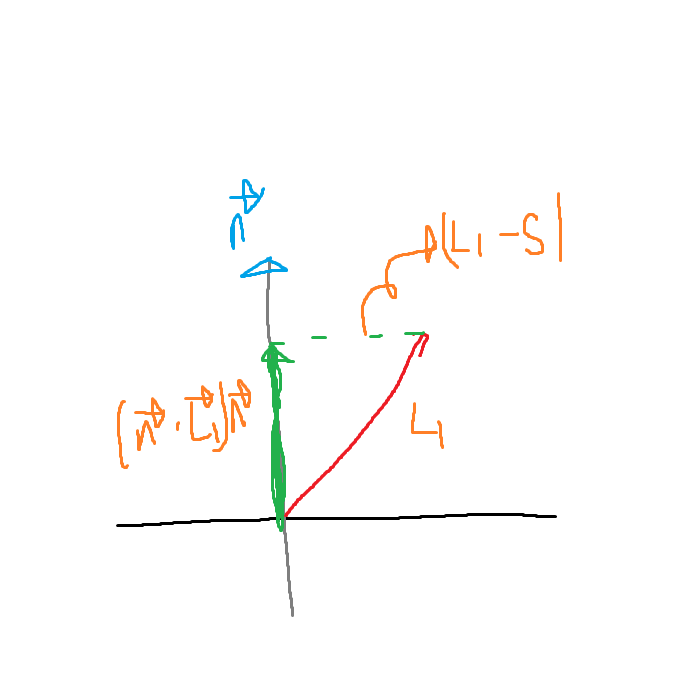
벡터 A는 L1-S1이다.
이제 A를 이용하면 L2 벡터를 구할 수 있다.
전반사이기 때문에 같은 각도로 반사돼었음을 이용하자.
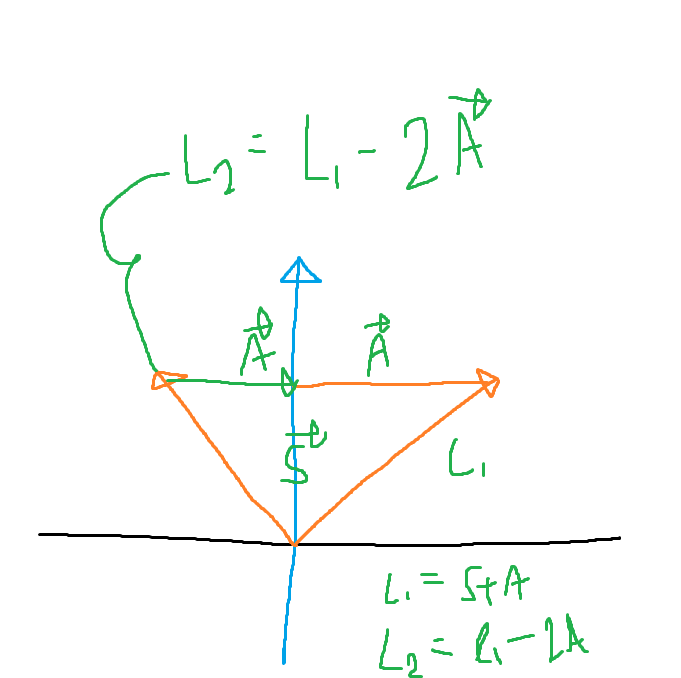
단순히 L1 벡터에서 A벡터를 2번 바꾸면 방향을 전환시킬 수 있다.
S = (n*L1)*n
A = L1 - (n*L1)*n
L2 = L1 - 2*(L1-(n*L1)*n)
이제 반짝임의 강도를 조절하는 상수를 L2와 곱하면 반짝임을 구할 수 있다.
참고: 홍정모의 그래픽스 강의
