홍정모 그래픽스 강의를 보고 삼각형과 벡터(광선)의 충돌을 판별하는 방법을 정리하는 글이다.
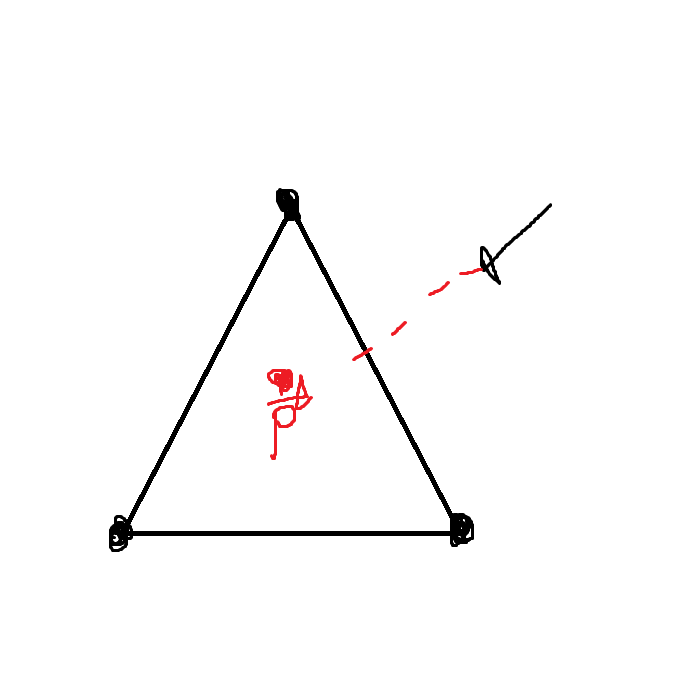
(삼각형 위의 점 벡터 P를 구하는 것이다.)
벡터 P를 수식으로 표현하면 다음처럼 표현할 수 있다.
O (origin: 광선이 출발하는 지점)
D (direction: 광선의 방향, 유닛벡터)
t (origin에서 P까지의 스칼라)
P (point: 광선과 충돌하는 삼각형 위의 점)
P = O + t*D
O,D는 광선이 시작하는 지점이니 알 수 있지만 t는 P가 어디에 있는지 알 수 없다.
우리의 목표는 이 t를 찾아서 P를 구하는것이다.
이 t는 외적을 사용하면 찾아낼 수 있다.
우선 삼각형의 normal 벡터를 찾아낸다.
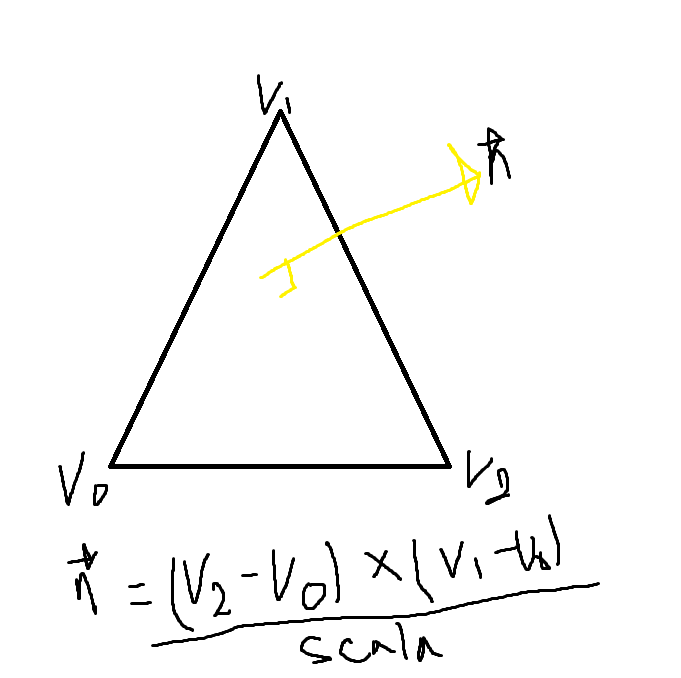
normal 벡터는 (V2-V0) x (V1-V0) / length(분자 벡터) 이다.
점 P는 삼각형 위에 있고 여기서 vertex와 P 사이의 벡터 (P-V0)와 normal 벡터의 내적은 수직임으로 항상 0이다.
이를 사용하여 t를 유도하자. 유도과정은 아래와 같다.
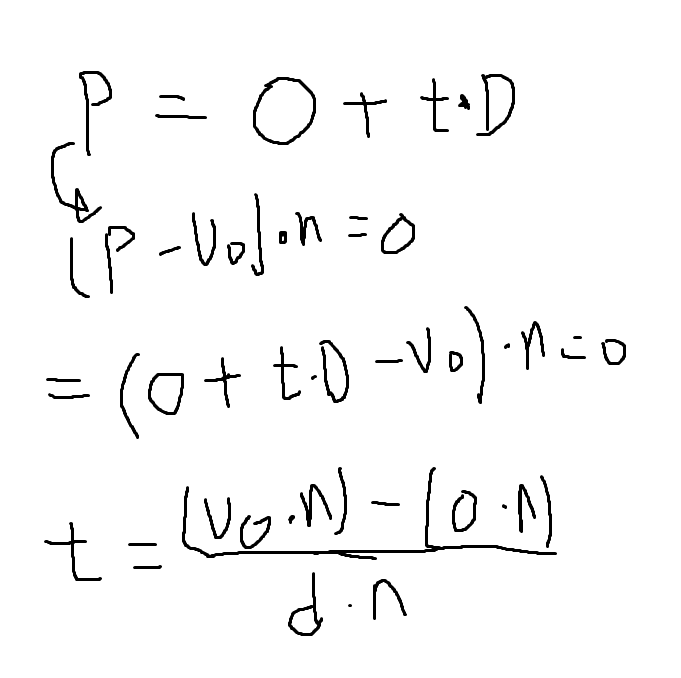
t를 구했음으로 P는 수식을 넣어서 구할 수 있다.
다음 과정은 P가 삼각형 내부에 있는지 판별해야한다.
삼각형 내부에 있는지 또한 외적을 사용하여 구할 수 있다.
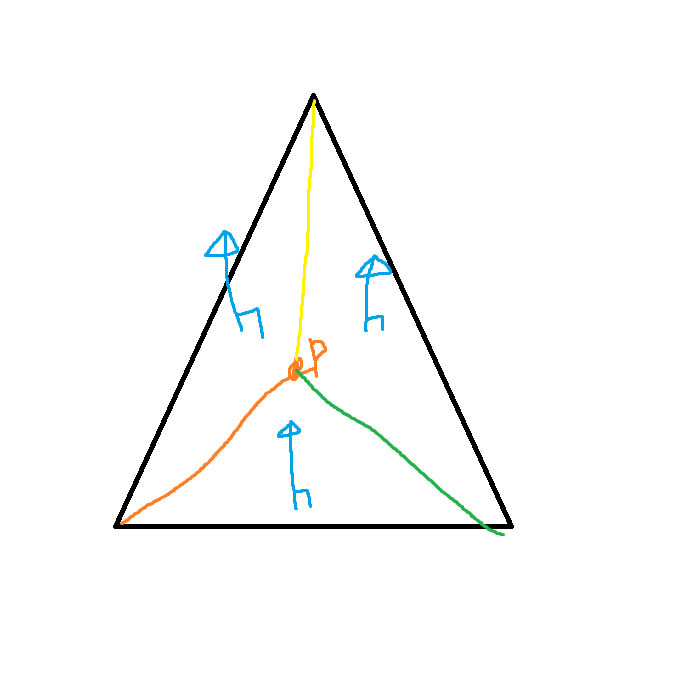
기본 아이디어는 다음과 같다. P를 중심으로 삼각형 내부를 더 쪼갠 후 각 삼각형의 normal 벡터를 구하여 전체 삼각형의 normal 벡터와 같은 방향을 바라보고 있는지 검사하면 된다.
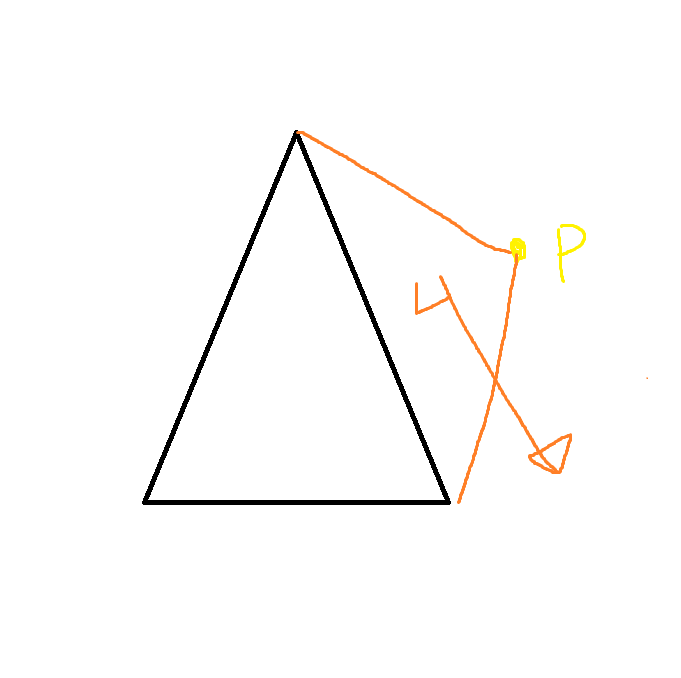
만약 P가 삼각형 외부에 있다면 외적시 normal 벡터와 반대방향으로 향하게 된다.
이제 P에 대해서 쪼개진 3가지 삼각형의 외적을 구한 후 0보다 작은지 비교하면 된다.
이때 주의해야할것이 있다.
Direct x에선 왼손 좌표계를 사용하고 있기 때문에 외적할때 방향을 잘 정해야 한다.
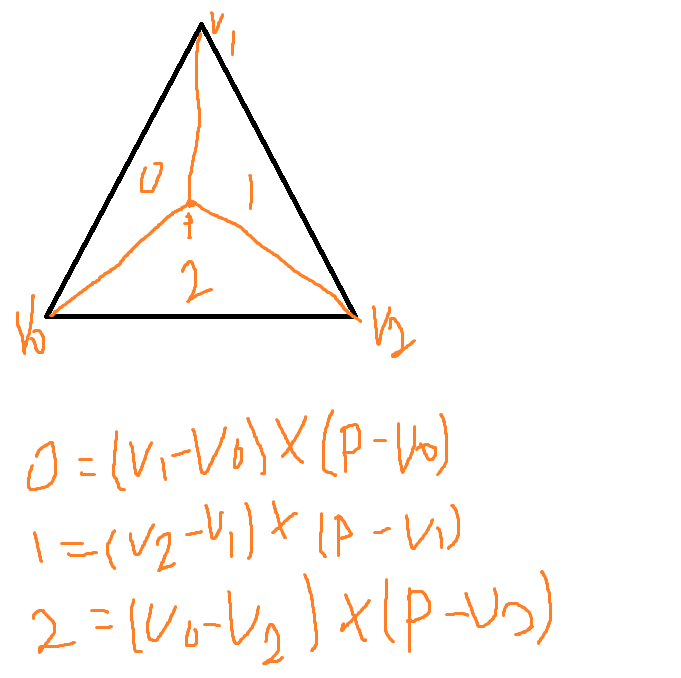
외적은 연산 방향이 달라지면 벡터의 방향도 달라진다.
이를 생각하면서 수식을 세우고 풀어야한다.
