무게중심 좌표계

Interpolation을 사용하는 좌표계이다.

삼각형 무게중심 좌표계는 아래와 같다.

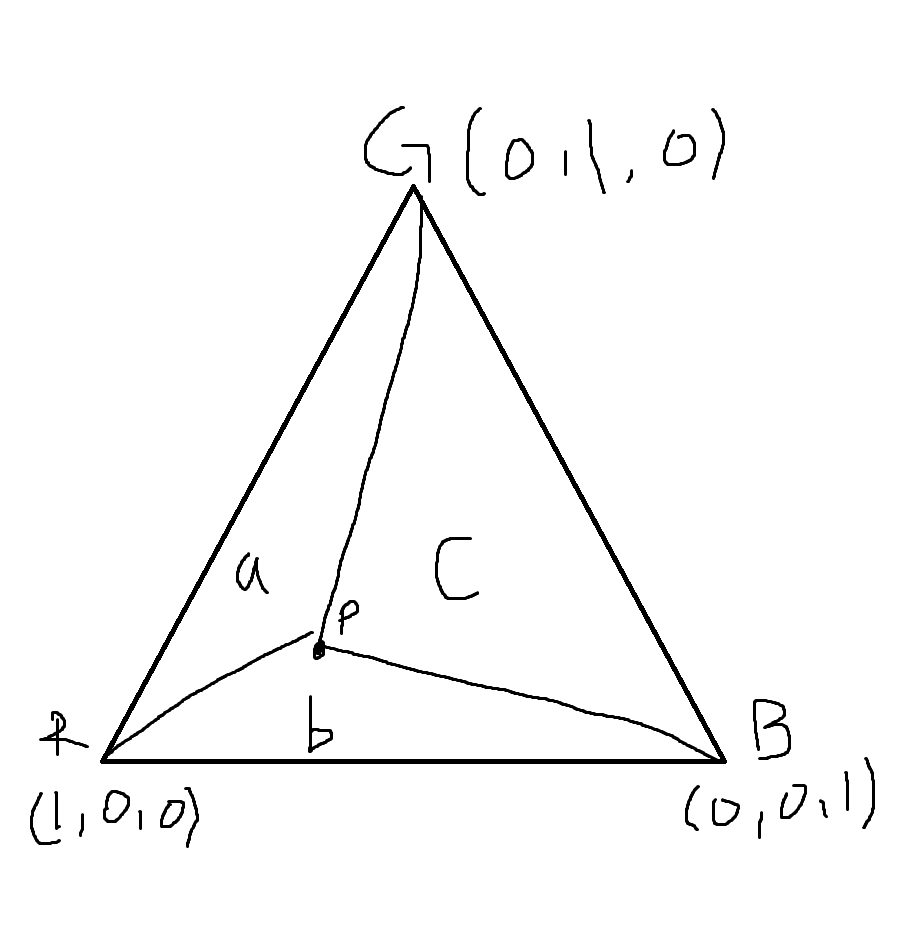
R(1,0,0), G(0,1,0), B(0,0,1) 로 구성된 삼각형이 있다.

여기서 P는 삼각형 내부에 있는 임의의 좌표이다. 이 좌표는 무게중심 좌표계를 사용하여 구할 수 있다.

그림을 자세히 보자.

1. P가 G에 가까워 질수록 b는 증가한다.
2. P가 B에 가까워질수록 a가 증가한다.
3. P가 R에 가까워질수록 c가 증가한다.

이러한 관계를 이용하여 식을 만들어내면 무게중심 좌표계를 만들 수 있다.

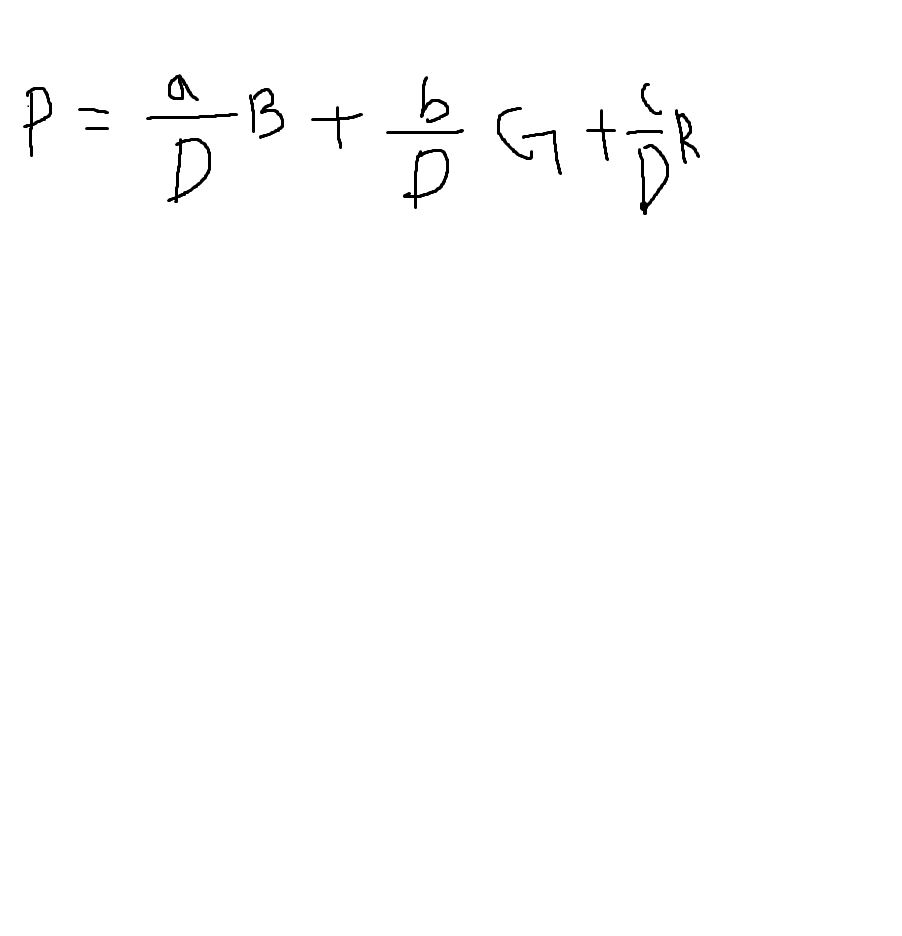
D = a+b+c 즉 전체 삼각형의 넓이이다.

a 삼각형의 넓이가 커질수록 B와 연산하여 나오는 벡터의 크기가 커진다.

마찬가지로 b의 넓이가 커질수록 G가 커진다.

동시에 c가 커질수록 R이 커진다.

왜 텍스처링에서 무게중심 좌표계가 나오냐면, 텍스처를 샘플링 할때 무게중심 좌표계를 사용하기 때문이다.

텍스처링

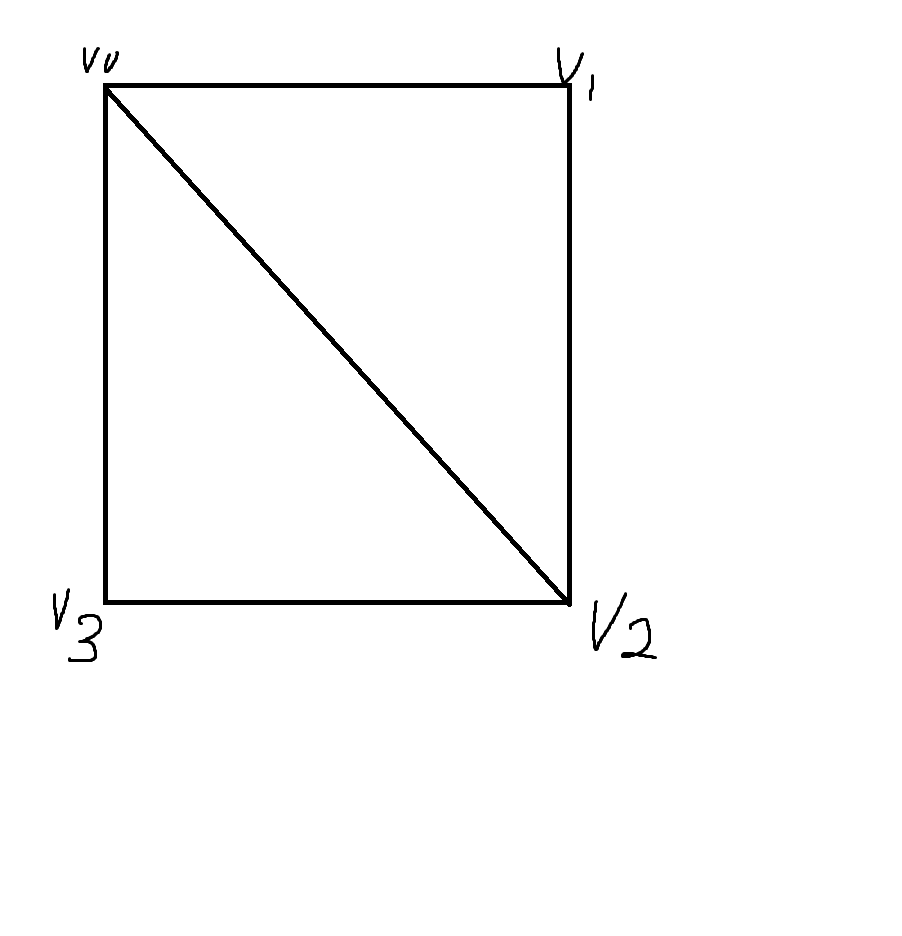
텍스처링은 물체에 이미지를 입히는 기술이다.

텍스처 매핑할대는 xy 좌표가 아닌 uv좌표계를 이용한다. (특별한 좌표계는 아니고 이름이 x->u, y->v로 바뀐것이다. )

보통 사각형을 그린다고 하면 2개의 삼각형으로 이뤄져있고 각 점(픽셀) 의 색상은 이미지에서 가져와 그린다.

이때 무게중심 좌표계를 사용하여 색상을 가져온다.

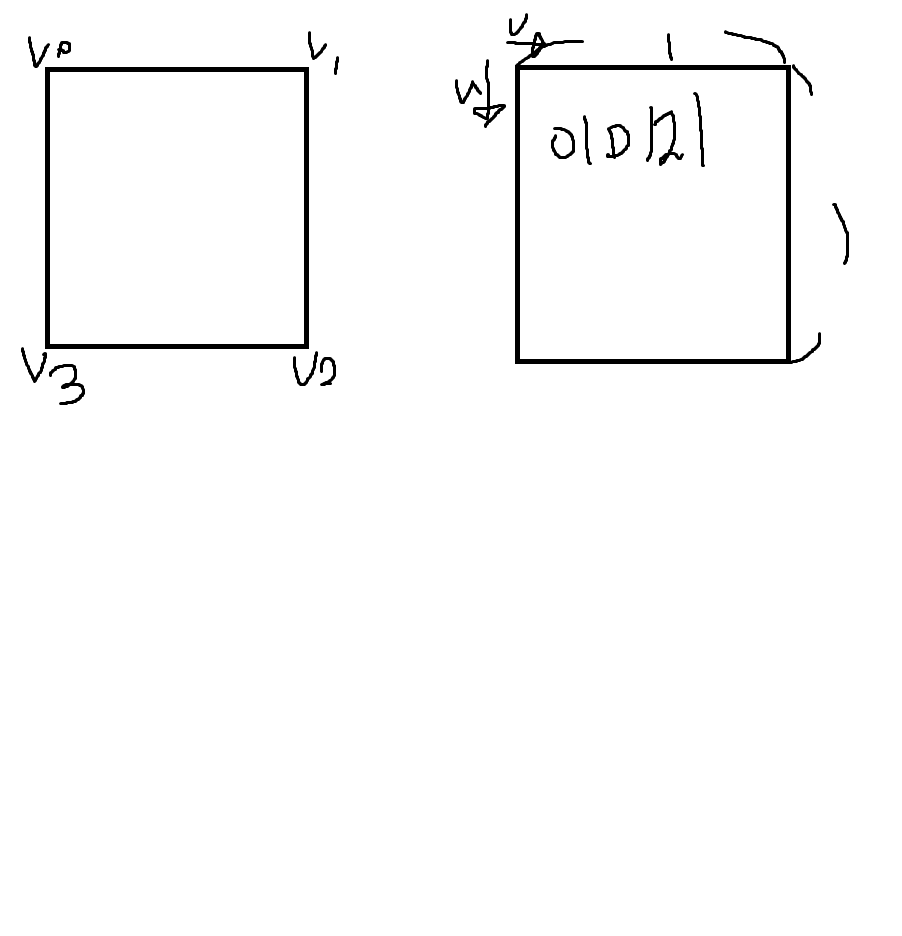
uv의 높이,넓이는 1이다.

쉐이더에서 샘플링은 직접하지 않고 tex2D라는 함수를 제공하고있다. 이를 사용하면 텍스처를 쉽게 입힐 수 있다.

샘플링

이미지를 그릴때 모든 이미지의 픽셀을 그대로 가져오면 연산에 무리가간다.

그래서 PointSampling, LinearSampling, SuperSampling등의 여러 기법을 사용하여 가져와 그린다.

자세한건 필요할때 검색해서 공부하는게 더 효율적이다.