변환

선형 변환 (Linear Transformation)

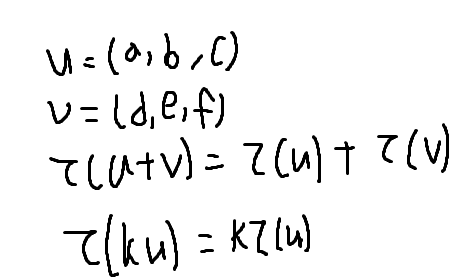
선형변환은 다음의 타우 함수를 만족하면 선형변환이다.

대표적으로 Scaling, Rotation은 선형변환을 만족한다.

이동은 선형변환이 아니다.

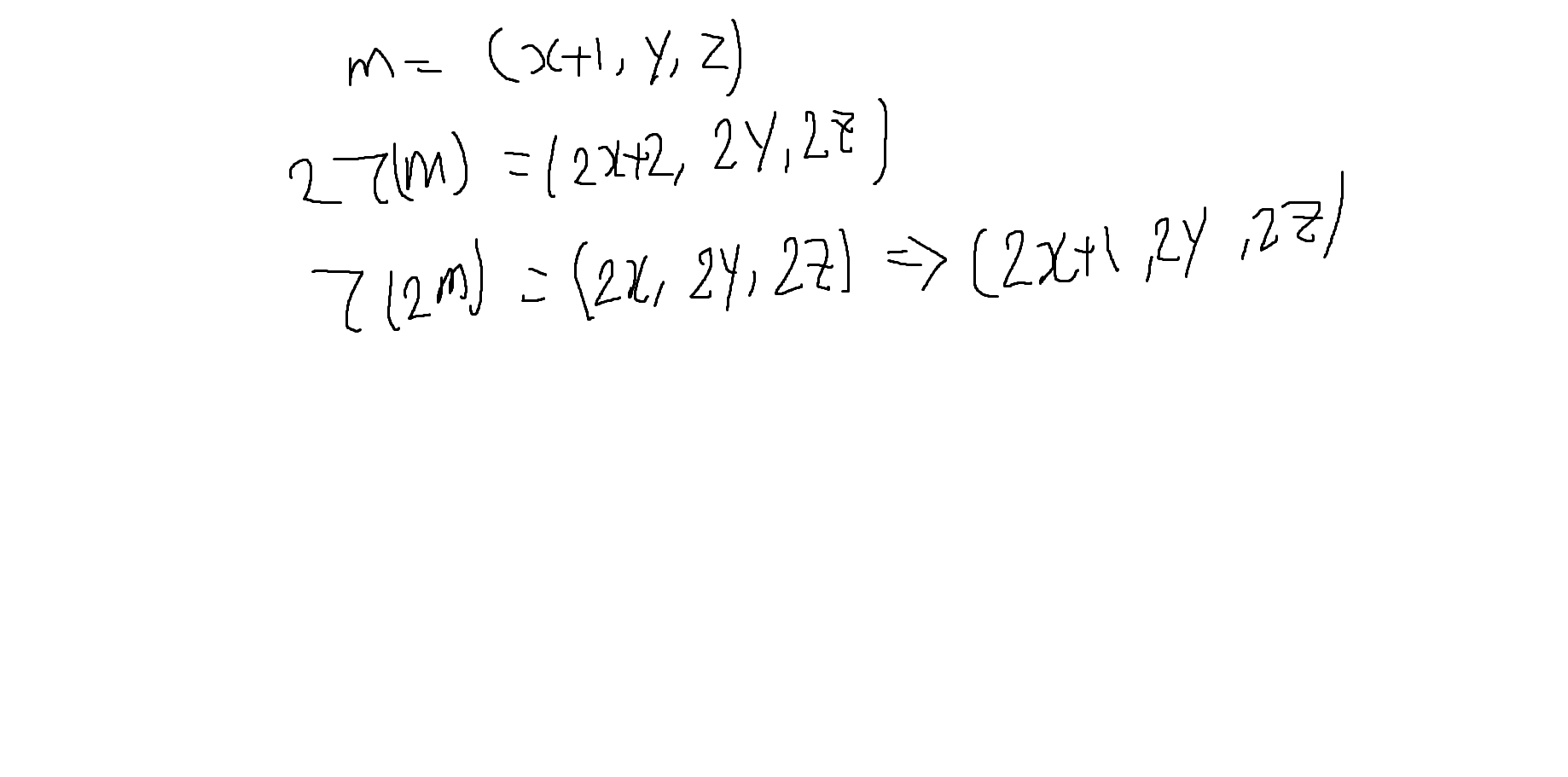
이 선형변환이 왜 중요하자면, 선형변환을 기저 벡터 (i,j,k) 를 사용하면 아래와 같이 u*A 형식의 행렬 연산으로 변환할 수 있다.

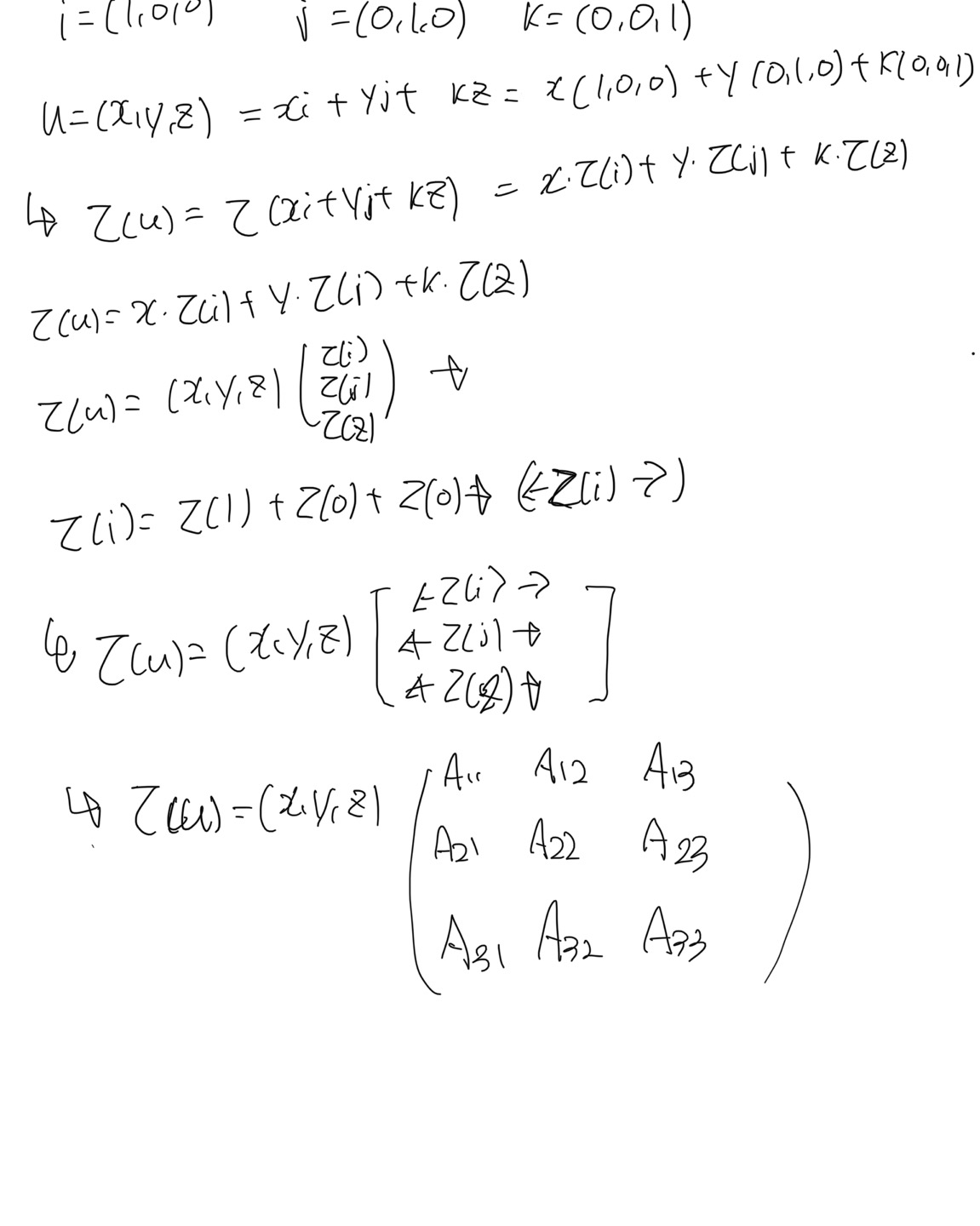
즉 선형변환을 만족하는 연산은 아래와 같은 행렬 곱으로 연산을 수행할 수 잇다는 말이 된다.

(캔버스에서 어떤 연산을 할때 행렬을 사용하는 이유도 선형 변환때문이다.

https://www.w3resource.com/html5-canvas/html5-canvas-matrix-transforms.php)

회전

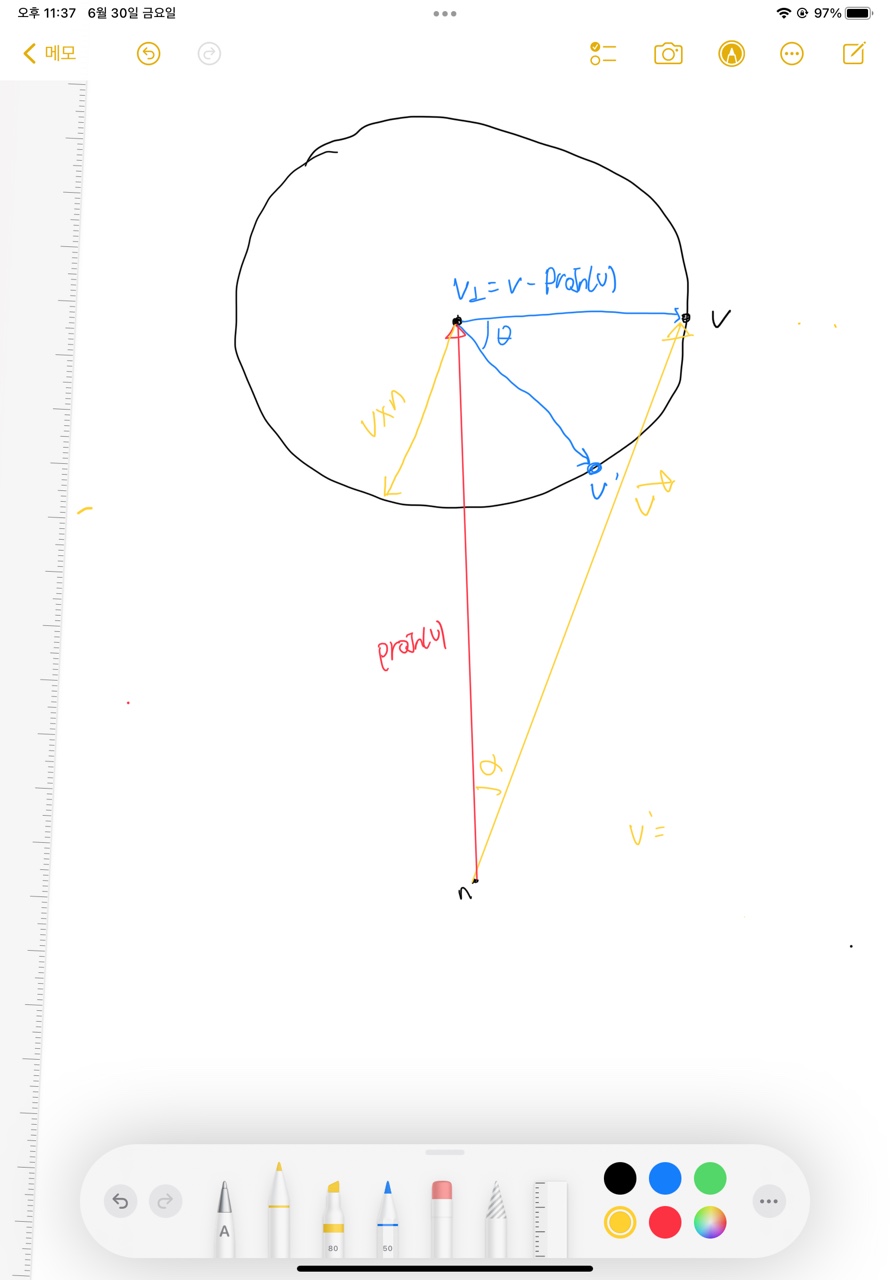
3차원에서 회전은 복잡하다.

우선 필요한것은 회전축 n과, 회전하는 원점 v가 필요하다.

여기서 벡터 n은 normalize vector이다.

포인트 n,v 로 가는 벡터를 벡터 V,

V를 n에 Projection 시킨 벡터를 Projn(V) 이다.

우선 2 정보를 활용하여 Vp 벡터를 구할 수 있다.

또한 cross product를 활용하여 n x v 벡터를 구하는것도 가능하다.

n x v 벡터는 벡터 n,v에 수직이기 때문에 평면을 정의할 수 있다.

Vp 벡터도 v에 수직이다. Vp 벡터와 n x v 벡터를 활용하여 원을 정의할 수 있다.

이제 다음 단계로 가보자.

|| n x v || === || Vp || 이다.

왜냐하면 n x v = |n||v|sin(alpha) => |v|*sin(alpha)

vp = |v|*sin(alpha) 이다.

따라서 두 벡터의 크기는 같다.

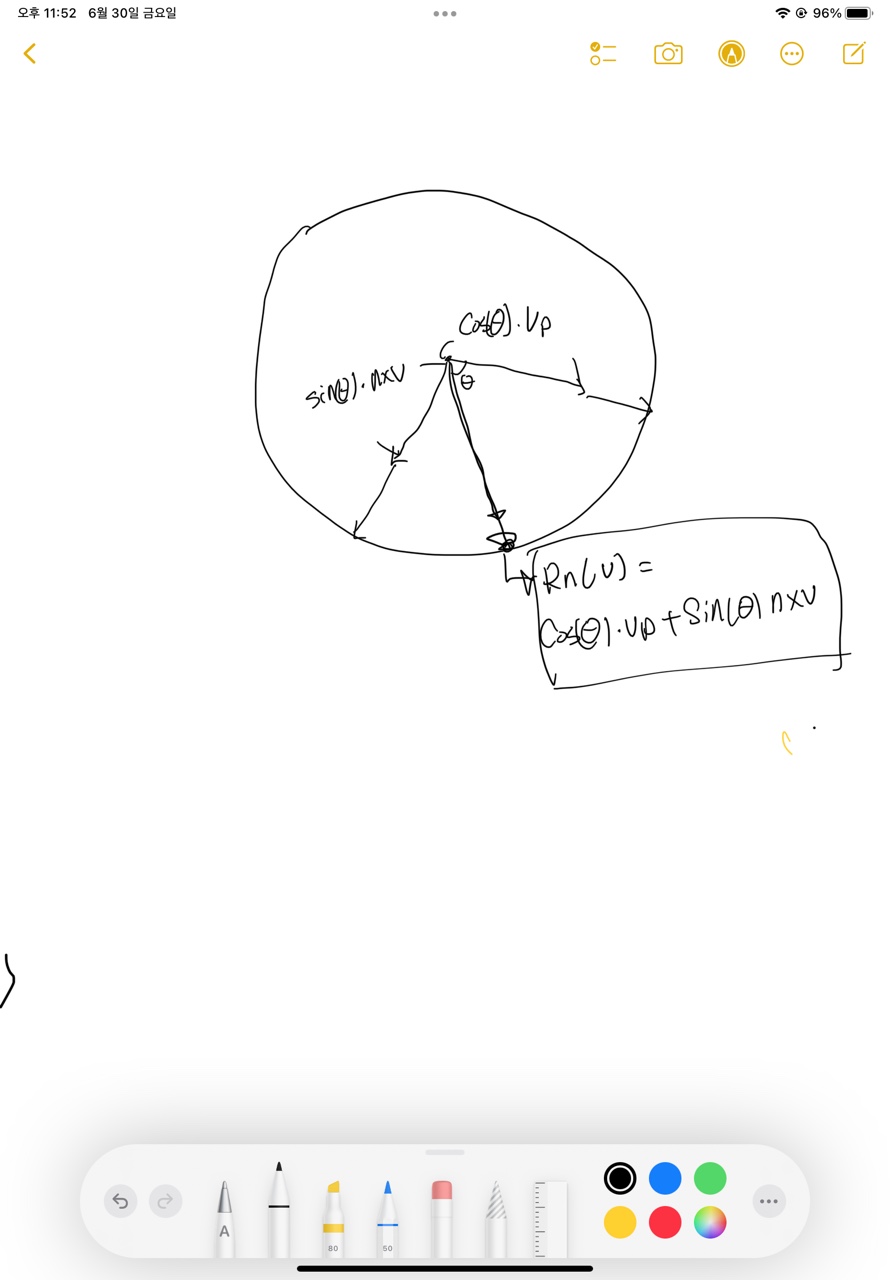
그후 찾은 Vp와 n x v 를 위에서 보면 위와같다.

움직인 결과인 Rn(V) 는 cos(theta)vp + sin(theta)nxv 수식을 이용하면 찾을 수 있다.

회전도 선형변환 이기 때문에 공식을 행렬로 연산할 수 있다.

보통 식을 직접 적어서 구하지 않고 제공하는 api나 라이브러리를 사용하기 때문에 원리만 알면 될 것 같다.

회전의 경우 역 연산이 필요할때 전치행렬을 사용하여 뒤집어 연산하면 가능하다. ( 회전은 전치행렬과 역행렬이 같다. )

아핀 변환

선형 변환과 이동을 하나의 행렬로 표현하는 방법이다.

Homogeneous Coordinates

• 벡터: (x,y,z,0) 뒤에 0이 있음. 이동이 불가능
• 벡터: (x,y,z,1) 뒤에 1이 있음.
• 포인트 - 포인트 (x,y,z,0) 벡터가 됨
• 포인트 + 벡터 = (x,y,z,1) 벡터가됨.

이 역시 캔버스에서 좌표계 변환을 할대 많이 봤을것이다.

bx,by,bz 값이 가장 아래에 있고 A 값들은 스케일, 회전 값을 넣는다.

회전과 변환을 더 쉽게 하기위한 도구들이다.