알고리즘 복잡도

오늘의 TMI
프로그래밍을 하는데 있어서 기초가 부족함을 느끼고 알고리즘과 컴퓨터 공학을 공부하고 있다.
비전공자로 소프트웨어 공학에 대한 기초지식이 없었는데, 이는 일을 하다보면 배워나가면서 해결할 수 있을 것이라 생각했다.
하지만 부족한 점이 많았고, 기초라도 확실하게 알고 일을 하고 싶은 마음에 처음부터 꼼꼼히 공부해 볼 생각이다.
컴퓨터 공학은 강의를 들으면서 전공자만큼은 아니더라도 일을 하는데 부족함이 없도록 공부하고, 자료구조와 알고리즘은 하나씩 익혀가며 코딩테스트를 통해 끊임없이 공부하고 테스트 해보려고 한다.

---

시간 복잡도

입력 크기의 값에 대해 단위 연산을 몇 번 수행하는지 계산하여, 알고리즘의 수행시간을 평가하는 방법

중요하지 않은 상수와 계수들을 제거하면 알고리즘의 실행시간에서 중요한

성장률에 집중할 수있는데 이것을 점근적 표기법(Asymptotic notation)이라 부른다.

여기서, 점근적이라는 의미는 가장 큰 영향을 주는 항만 계산한다는 의미다.

빅오

최악의 상황을 고려하여 성능 측정 결과 표현

세타

평균적인 경우에서의 성능 측정 결과 표현

오메가

최선의 상황일 때의 성능 측정 결과 표현

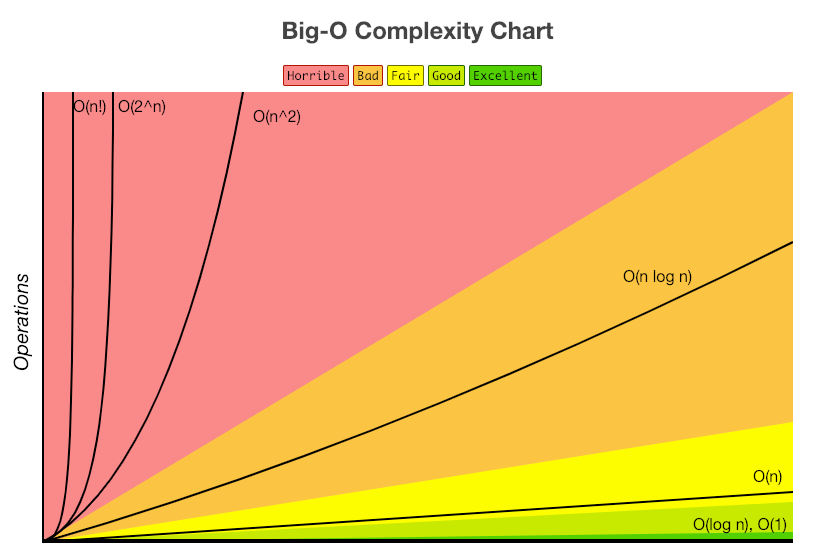
빅오

빅오 표기법의 경우 for문이 얼마나 많이 중첩되어 있냐에 따라 n의 제곱, 세제곱으로 커지게 된다.

O(1)

아래처럼 총 3회의 코드가 수행되게 되고, 상수를 가지게 되면 O(1)으로 표기

function big_o(n) {
	let sum = 0; // 1회
	sum = n * 2; // 1회
	return sum; // 1회
}

O(N)

n+2회 돌게 되는데, 이 때 상수인 2는 n에 비해 영향을 미치지 않기 때문에 생략한다.

function big_o(arr, n) {
	let sum = 0; // 1회
	for (let i = 0; i < n; i++){ // n회
		sum += arr[i];
	}
	return sum; // 1회
}

O(N^2)

n^2 + 2

for문이 두 번 중첩되어 있기 때문에 N^2가 된다.

만약 n^2 + n + 2 가 되더라도 가장 높은 차수가 영향을 미치기 때문에 O(N^2)가 된다.

function big_o(arr, n) {
	let sum = 0; // 1회
	for (let i = 0; i < n; i++){ // n번만큼 돈다.
		for (let j = 0; j < n; j++) { // n번만큼 돈다.
				sum += arr[i][j];
		}
	}
	return sum; // 1회
}

O(logN)

n/2 + 2 이기 때문에 logN이 된다. 만약 i *= 3 이라면 log_3N이 된다.

O(logN)의 경우 O(N)보다 효율적이다.

function big_o(n) {
	let sum = 0;
	for(let i = 0; i < n; i *= 2) { // n/2회
		sum += 2;
	}
	return sum;
}