1. Introduction

---

LM의 output에 대한 'uncertainty'를 정확히 측정할 수 없다면 (application 상황에서) 우리는 해당 output에 대한 일관성에 의구심을 가질 수 밖에 없다.

하지만 자연어 생성 task는 '비정형 데이터'를 생성하고 평가하는 문제이기 때문에 (논문에서는 free-form NLG라고 명명함) 'uncertainty'를 명확히 측정하는 것은 굉장히 제한적이다.

그리고 우리가 언어라는 것을 바라볼 때는 기본적으로 '의미(semantic)'과 '형태(lexical)'을 동시에 고려하지만, 현재의 LM들의 token-likelihood 기반의 학습 방법들은 lexical confidence만을 강화하는 방법들로 학습이 되어왔다. 그렇지만, 정작 application 단으로 넘어가면 LM이 생성된 문장들의 의미가 중요해진다. (저자들이 아래에 가져온 예시들을 살펴보자)

LM이'France’s capital is Paris'을 생성할지 아니면 'Paris is France’s capital'을 생성할지 'uncertainty'해도 실제 두 문장이 의미하는 바가 같기 때문에 같은 대답이라고 해야한다. 하지만 현재의 LM들은 token 단위로 학습되기 때문에 (같은 의미를 같는) 위의 2개의 대답에 대한 불확실성을 굉장히 높게 평가한다. (의미론적으로 보면 분포상 한점에 높은 밀도 안에 모여 있어야하는 대답들임에도 불구하고)

이러한 semantic equivalence을 설명하기 위해 저자들은 semantic likelihood를 측정하는 기법을 제시한다. 저자들이 제시하는 알고리즘은 간단하다. 한 문장으로 다른 문장의 의미를 추론할 수 있다면 두 문장은 같은 의미를 같다고 가정할 수 있고, 이 가정을 바탕으로 여러 군집들은 만든다. 만들어진 군집들은 확률의 개념을 도입해 엔트로피를 측정해 LM의 ouput의 semantic uncertainty를 측정하는데 활용된다.

2. Background on Uncertainty Estimation

---

예측의 불확실성은 output distribution의 예측가능한 entropy로 측정할 수 있으며, 데이터 point x에 대한 y의 조건부 entropy는 다음과 같이 정의될 수 있다.

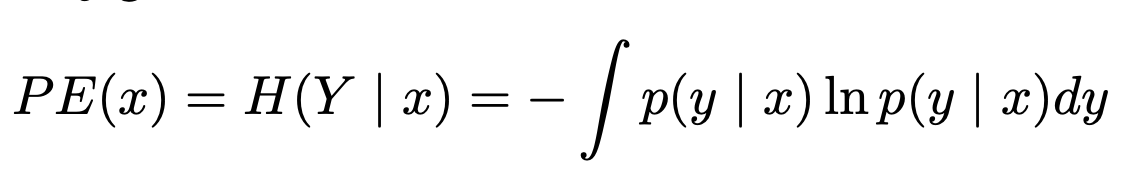
일반적으로 Entropy는 누락된 데이터 분포에 내제된 노이즈로부터 파생된 'aleatoric uncertainty'와 모델이 데이터를 충분히 학습하지 못해 파라미터에 내제된 'epistemic uncertainty'로 구분된다. LM이 생성하는 output은 'epistemic uncertainty'로 구분지을 있기에 본논문에서는 'epistemic uncertainty'에 집중한다.

'epistemic uncertainty'은 일반적으로 'mutual information'으로 측정되는데,

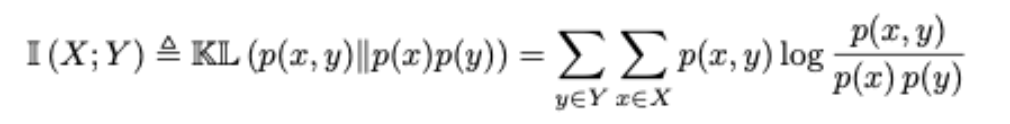
NLP 분야에서는 이를 위해서는 여러 LM들의 output들을 ensemble해 위의 수식을 적분해야하기 때문에 비효율적이라는 문제가 있다고 한다.

또한 introduction에서 지적한바와 같이 product of the conditional probabilities of new tokens given past tokens로 output sequence의 likelihood를 구하는 것은 output의 semantic을 제대로 구하는데 한계가 존재한다.

3. CHALLENGES IN UNCERTAINTY ESTIMATION FOR NLG

---

NLP가 다른 분야와 달리 불확실성을 측정하기 어려운 이유는 output들이 완전히 상호 베타적이지 않기 때문이다. 위의 예시를 가지고 오면 'France’s capital is Paris'와 'Paris is France’s capital'는 lexical & syntax 측면에서 완전히 다른 output이지만 semantic 측면에서 완전히 동일한 output이기에 완전히 상호 베타적으로 분류할 수 없다.

따라서 본 논문에서는 'semantic equivalence', 의미적으로 동일한 output을 estimation 해내는 방법론을 제시한다.

$N$개의 token들로 이루어진 각각의 sequence가 하나의 의미를 가지고 있다고 할 때, sequence equivalence relation을 정의하기 위해 저자들은 $E(\cdot,\cdot)$라는 placeholder를 정의한다. 이 placeholder는 reflexive(for all x, x=x), symmetric (for all real numbers x and y ,if x=y, then y=x), transitive (for all real numbers x,y, and z, if x=y and y=z, then x=z)하다. Sequence equivalence relation은 semantic equivalence class를 정의하기 위해 활용되며 하나의 semantic equivalence class는 1개의 의미만을 가질 수 있다.

일반적으로 LM의 conditional output은 $p(s|x)$로 정의하지만, semantic equivalence class에 대한 확률을 정의하기 위해 논문에서는 LM이 equivalence class로 생성한 output distribution에 대해서 전부 다 더해 아래와 같은 수식을 제안한다.

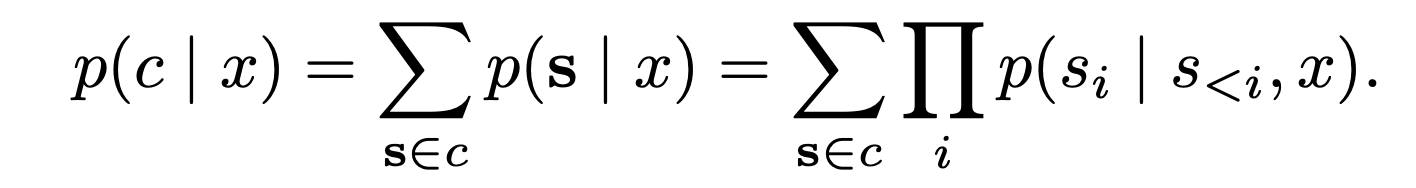
4. SEMANTIC UNCERTAINTY

---

저자들이 제시하는 meaning space에서 uncertainty를 측정하는 방법은 크게 3가지 단계로 나누어진다.

Step 01. Generating s set of answers from the model

1개의 LM에 대해서 $M$개의 sequence ${\{s^1,s^2,...,s^M}\}$들을 생성하였다. (데이터셋은 Q&A 데이터셋을 활용했는데, 하나의 question에 대해서 한 모델이 multinomial sampling & multinomial beam sampling을 통해 $M$개의 answer pair를 만들었다고 보면 된다)

선행연구와는 달리 ensemble models들을 쓰지 않아 independent foundation models training cost가 없다는 장점을 지속적으로 어필하고 있음

Step 02. Clustering by semantic equivalence

위의 section 03에서 정의한 equivalence relation $E(\cdot,\cdot)$와 MNLI dataset으로 finetuning한 Deberta-large model을 활용해 생성한 $M$개의 sequence ${\{s^1,s^2,...,s^M}\}$들을 clustering한다.

방법은 아래 알고리즘에 나와있는데로 서로 다른 sequence들을 context들과 함께 concat해 bidirectional한 방향으로 2번 inference해서 모두 entailment가 나오면 하나의 cluster로 분류하고 아니면 다른 cluster로 분류하는 식이다.

Step 03. Computing the semantic entropy

Step 02에서 sequence별로 cluster가 구해졌다면 동일한 cluster에 속한 generated sequence들 별로 likelihood들을 더한 후 semantic entropy를 계산하였다.

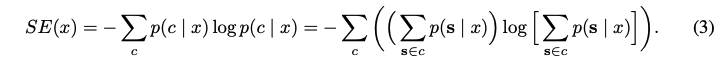
저자들은 모든 가능한 meaning class $c$를 활용하지 않고 Monte Carlo integration을 활용해 몇개만을 sampling해서 활용했다고 한다.

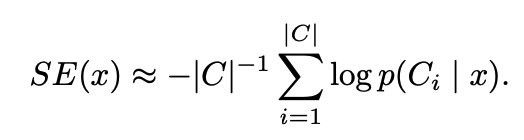
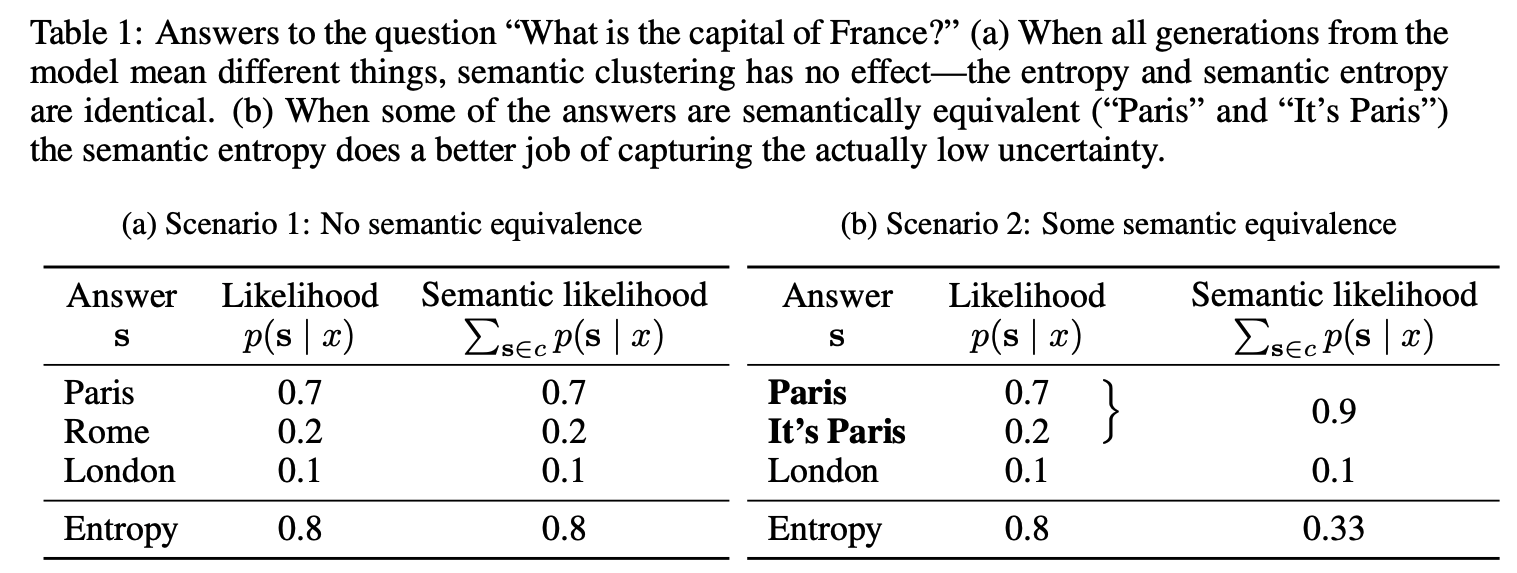
저자들이 아래 첨부한 Table을 보면 LM이 유사한 대답을 하는 상황에서 Semantic Likelihood는 vanilla Likelihood에 비해 LM의 대답이 상대적으로 덜 uncertainty하다는 것을 잡아내고 있음.

5. Empirical Evaluation

---

MODEL: OPT (2.7B, 6.7B, 13B and 30B parameters)
DATASET: CoQA & TriviaQA
$ROUGE-L(S,S')>0.3 9)$ (Appendix에서 Robustness 검증함) (reference 문장이랑 모델이 생성한 문장이랑 rouge-lcs가 0.3이상이면 postive라고 분류했다고 보는듯)
METRIC: AUROC

(논문에 앞에까지 계속 Semantic Entropy로 Estimation한다고 이야기하다가 갑자기 AUROC 계산 한다는 이야기가 나와서.. 이부분은 여전히 이해가 가지를 않습니다...)

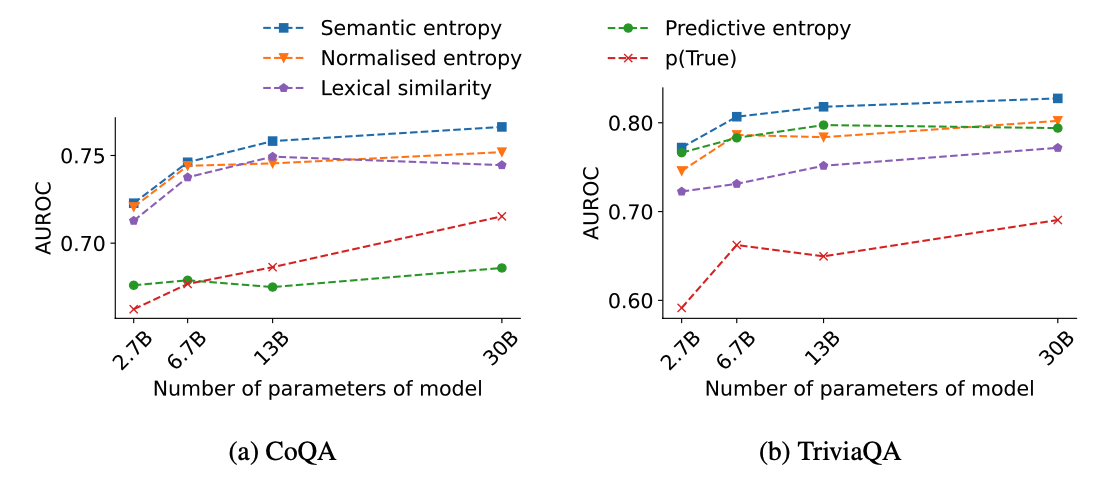
• Fig. 1a) we show that semantic entropy has a significantly higher AUROC than entropy in sequence-probability- space with and without length-normalisation, as well as the lexical similarity baseline. At the same time, it performs dramatically better than p(True).
• Fig. 1b) that our method out- performs more for larger model sizes and continues to steadily improve as the model size increases.

또한 incorrect하게 답할수록 더 많은 semantically distinct한 cluster를 하는 것도 보였습니다. (LM이 생성하는 대답이 uncertainty하다 > (한질문에 대해서) semantically하게 퍼져있는 대답을 생성한다)