www.acmicpc.net/problem/1003
#다이나믹프로그래밍
DP 재귀 풀이법
재귀호출을 할 때 이미 한 번 탐색(연산)했던 값이 있다면 또다시 연산하는 것이 아니라 이미 계산된 값을 재사용하여 반복적인 연산과정을 줄이는 방법이 DP풀이의 기초다.
이전 글에서는 피보나치 수를 배열에 담아 만약 해당 배열에 값이 없다면 fibonacci(N - 1) + fibonacci(N - 2) 을 통해 재귀호출을 해주었고, 만약 배열에 값이 있다면(이미 이전에 호출했었던 N이라면) 해당 배열값을 바로 반환해주었다.
이번 문제는 그럼 DP로 어떻게 접근해야 할까?
일단, 이번 문제는 피보나치 수를 구하는 것이 아니라 피보나치 수에서 0과 1이 호출되는 횟수를 구하는 것이다.
예로들자면 이런 것이다.
N=2 일 때, Fibonacci(2) = Fibonacci(1) + Fibonacci(0) 이므로 0과 1은 각각 1번씩 호출된다.
N=3 일때는 Fibonacci(3) = Fibonacci(2) + Fibonacci(1) 이고 이는 다시
Fibonacci(3) = (Fibonacci(1) + FibonaccI(0)) + Fibonacci(1) 이므로 0은 1번, 1은 2번 호출된다.
이렇게 N에대하여 각 0과 1이 호출된 횟수를 저장하면 되지 않겠는가?
간단하게 생각해보자. 만약 처음에 N=20 이 입력되어 20에 대해 0과 1 호출횟수를 구한다면 Fibonacci(19) 에 대해서도 자연스럽게 구해질 것이고, Fibonacci(18), Fibonacci(17), ⋯ 해서 N 이하의 모든 수들은 자연스럽게 0과 1을 찾기위해 하위단계로 재귀호출될 것이다.
즉, N=20 에 대해 구한다음에 만약 N=15 같이 이하의 수가 입력된다면 또 다시 재귀호출 할 필요 없이 이미 연산과정에서 한 번 탐색이 이루어졌으므로 바로 해당 값을 꺼내면 된다.
이 과정을 DP로 풀어내면 된다는 의미다. 즉, 한 번 탐색할 때마다 해당 N의 0과 1의 값을 저장해두고, 이후 다음 탐색에서 이미 탐색했던 노드일 경우 해당 배열값을 쓰면 된다.
코드로는 N이 최대 40 까지 주어지고, 각 N에 0과 1이 호출된 횟수를 담아야 하므로 2차원 배열이 있어야겠다. (또한 null 체크를 하기 위해 int[][] 배열이 아닌 Integer[][] 배열로 쓸 것이다. int[][] 배열을 쓰고자 한다면 모든 배열의 값을 -1 과 같은 값으로 모두 초기화 해주길 바란다.)
static Integer[][] dp = new Integer[41][2];
dp[0][0] = 1; // N=0 일 때의 0 호출 횟수
dp[0][1] = 0; // N=0 일 때의 1 호출 횟수
dp[1][0] = 0; // N=1 일 때의 0 호출 횟수
dp[1][1] = 1; // N=1 일 때의 1 호출 횟수
statc Integer[] fibonacci(int N) {
// N에 대한 0, 1의 호출 횟수가 없을 떄(탐색하지 않은 값일 때)
if(dp[N][0] == null || dp[N][1] == null) {
// 각 N에 대한 0 호출 횟수와 1 호출 횟수를 재귀호출한다.
dp[N][0] = fibonacci(N - 1)[0] + fibonacci(N - 2)[0];
dp[N][1] = fibonacci(N - 1)[1] + fibonacci(N - 2)[1];
}
// N에 대한 0과 1, 즉 [N][0]과 [N][1] 을 담고있는 [N]을 반환한다.
return dp[N];
}위와 같은 알고리즘을 통해 풀어낼 수 있다.
dp 라는 배열을 선언하고, 피보나치 함수는 각 N에 대한 0과 1의 값을 dp에 저장하면서 재귀호출을 해주는 것이다.
이 방법이 문제의 취지에 가장 정석적인(?) 방법이지 않을까 생각된다.
DP 반복문 풀이법
대부분의 알고리즘은 규칙성이 있다는 것, 즉 수식화 할 수 있다. 간단하게 말해서 N=0 부터 시작하여 몇 개를 쭉 나열하다보면 규칙성이 보일 가능성이 높다는 것이다.
한 번 쭉 나열해보자.
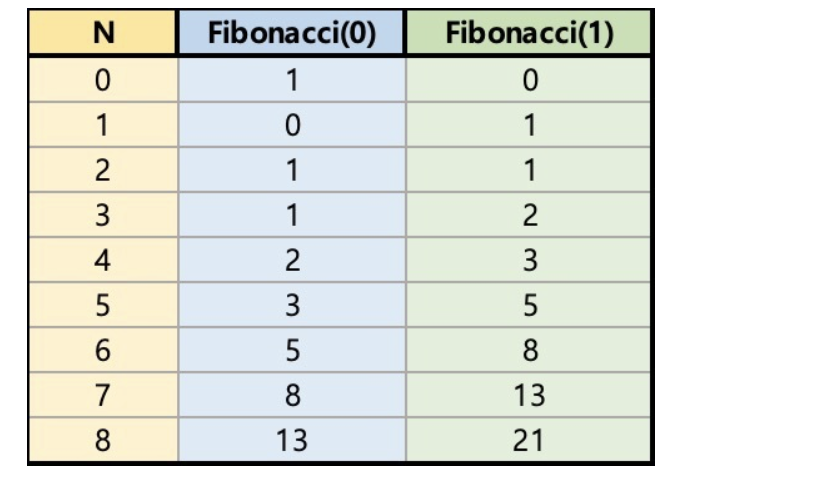
규칙성이 보이는가?
보면 N에 대한 0과 1은 다음과 같은 규칙을 따른다.
1. N에 대한 0호출 횟수 = N-1의 1 호출 횟수
2. N에 대한 1 호출 횟수 = N-1의 0 호출 횟수 + N-1의 1 호출 횟수
위 규칙을 반복문으로 풀자면 다음과 같다.
// 기본 값(N=0일 때)
int zero = 1;
int one = 0;
int zero_plus_one = 1;
for (int i = 0; i < N; i++) {
zero = one; // 0호출 횟수를 이전의 1호출 횟수로 변경
one = zero_plus_one; // 1호출 횟수를 이전의 0과 1호출 횟수의 합으로 변경
zero_plus_one = zero + one; // 0과 1 호출의 합 계산
}
이렇게 하여 N에대한 0과 1 호출 횟수를 쉽게 구할 수 있다.
package baekjoon_java.SilverIII;
import java.util.Scanner;
public class 피보나치함수 {
static Integer[][] dp = new Integer[41][2];
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
dp[0][0] = 1; // N=0 일 때의 0 호출 횟수
dp[0][1] = 0; // N=0 일 때의 1 호출 횟수
dp[1][0] = 0; // N=1 일 때의 0 호출 횟수
dp[1][1] = 1; // N=1 일 때의 1 호출 횟수
int T = in.nextInt();
StringBuilder sb = new StringBuilder();
while(T-- > 0){
int N = in.nextInt();
fibonacci(N);
sb.append(dp[N][0] + " " + dp[N][1]).append('\n');
}
System.out.print(sb);
}
static Integer[] fibonacci(int N) {
// N에 대한 0, 1의 호출 횟수가 없을 떄(탐색하지 않은 값일 때)
if(dp[N][0] == null || dp[N][1] == null) {
// 각 N에 대한 0 호출 횟수와 1 호출 횟수를 재귀호출한다.
dp[N][0] = fibonacci(N - 1)[0] + fibonacci(N - 2)[0];
dp[N][1] = fibonacci(N - 1)[1] + fibonacci(N - 2)[1];
}
// N에 대한 0과 1, 즉 [N][0]과 [N][1] 을 담고있는 [N]을 반환한다.
return dp[N];
}
}
