[Silver III][JAVA]2579번:계단 오르기

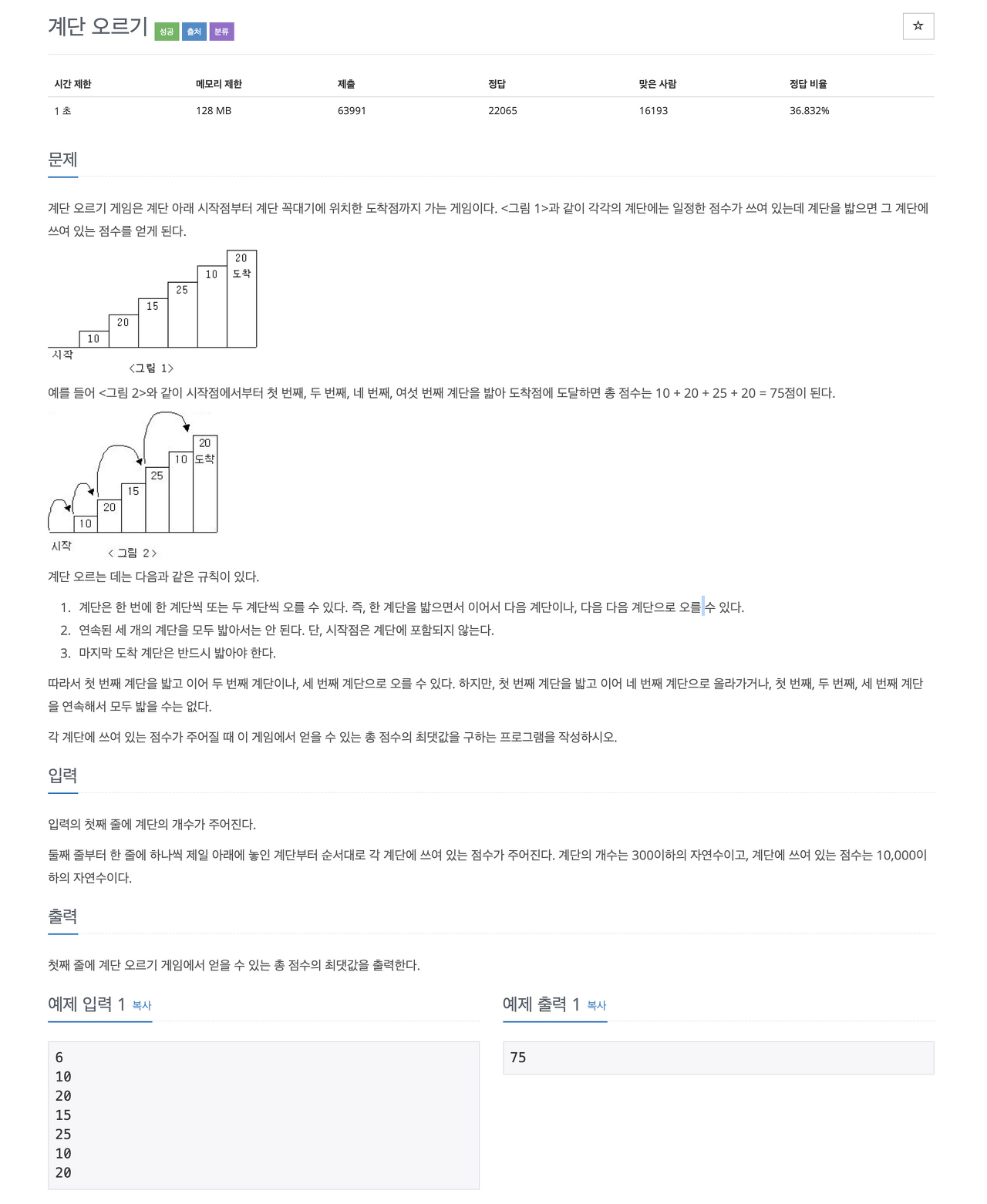
STEP1 초기값 설정해주기

dp[0] = 0;
dp[1] = stair[1];
if (N >= 2) {
	dp[2] = stair[1] + stair[2];
}

dp배열: 각 계단의 최댓값을 표현하는 배열
stair배열: 입력값

if문으로 dp [2]를 해준 이유는 어떠한 값이더라도 계단이 2개 이상이라면 2번째 계단의 최댓값은 첫 번째 계단과 2번째 계단을 더한 값과 같기 때문입니다.

STEP2 문제 이해하기 + 재귀 구현하기

마지막 계단(N번째 계단) 기준에서 생각해보면 2가지 케이스가 나옵니다.
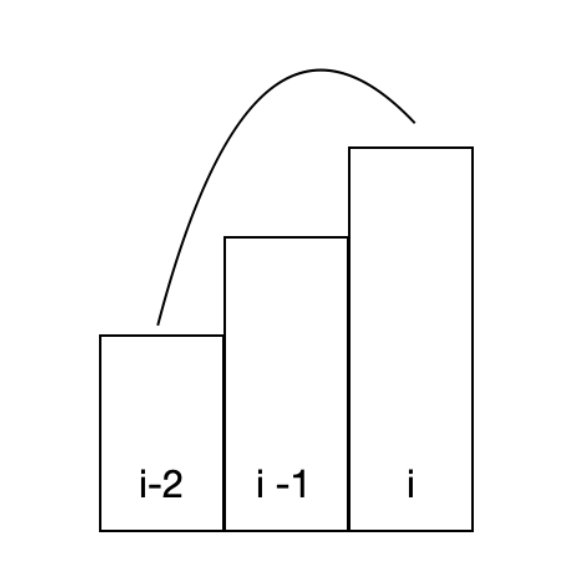
1. dp[i-2] + stair[i]
두 계단으로 바로 올라온 경우

2. dp[i-3] + stair[i-1] + stair[i]
   두 계단 + 한 계단으로 올라온 경우 (연속된 3개x)
   

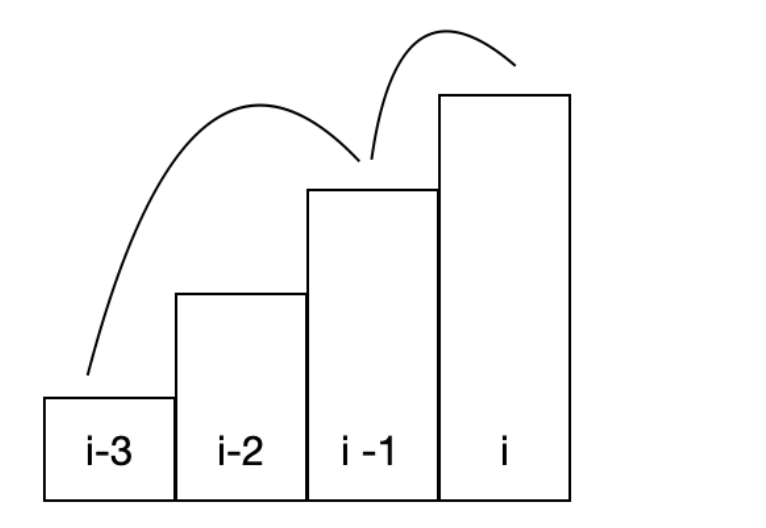
점화식 :dp[i] =  Math.max(dp[i-3] + stair[i-1] + stair[i], dp[i-2] + stair[i]);

전체코드:

package baekjoon_java.SilverIII;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
/**
 * 백준 2579 계단 오르기 (https://www.acmicpc.net/problem/2579)
 */
public class 계단오르기 {
    static int N;
    static Integer[] stair;
    static Integer[] dp;

    public static void main(String[] arg) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());

        stair = new Integer[N + 1];
        dp = new Integer[N + 1];

        for (int i = 1; i < N+1; i++) {
            stair[i] = Integer.parseInt(br.readLine());
        }

        //dp : 각 단계별 최댓값
        dp[0] = 0;
        dp[1] = stair[1];
        if (N >= 2) {
            dp[2] = stair[1] + stair[2];
        }

        for (int i = 3; i < N+1; i++) {
            // 1. 두 계단 + 한 계단 오른 경우
            // 2. 한 번에 두 계단 오른 경우
            dp[i] = Math.max(dp[i - 3] + stair[i - 1] + stair[i], dp[i - 2] + stair[i]);
        }

        System.out.println(dp[N]);
    }
}