dynamic programming, DP
: 여러 개의 하위 문제를 먼저 푼 후 그 결과를 쌓아올려 주어진 문제를 해결하는 알고리즘
- 데이블 정의하기
- 점화식 찾기
- 초기값 설정
Dynamic Programming (동적 계획법) 조건
- 재귀(Recursion)란?
- 자기 자신을 호출하는 함수로 반복적으로 호출을 함으로써 원하는 결과를 도출 할 수 있습니다.
- 메모이제이션(Memoization)이란?
- ‘중복 계산'을 피하기 위한 기법입니다. 이를 이용하여 이전에 계산된 결과를 저장하고 다음에 동일한 계산에 필요할 때 저장된 결과를 이용하여 중복 계산을 피함으로써 성능을 향상 시킬 수 있습니다.
▶ 재귀
동적계획법의 등장은 피보나치 수열이라고 한다. 피보나치 수열은 대표적인 재귀함수로, 아래와 같이 표현할 수 있다.
public class Fibonacci {
public static int fibo(int n) {
if (n <= 1) {
return n;
}
return fibo(n - 1) + fibo(n - 2);
}
public static void main(String[] args) {
int n = 10; // 원하는 숫자
System.out.println("Fibonacci of " + n + " is: " + fibo(n));
}
}만약 fibo(7) 을 구하는 과정을 도식화 해보면, 아래 이진 트리와 같다.
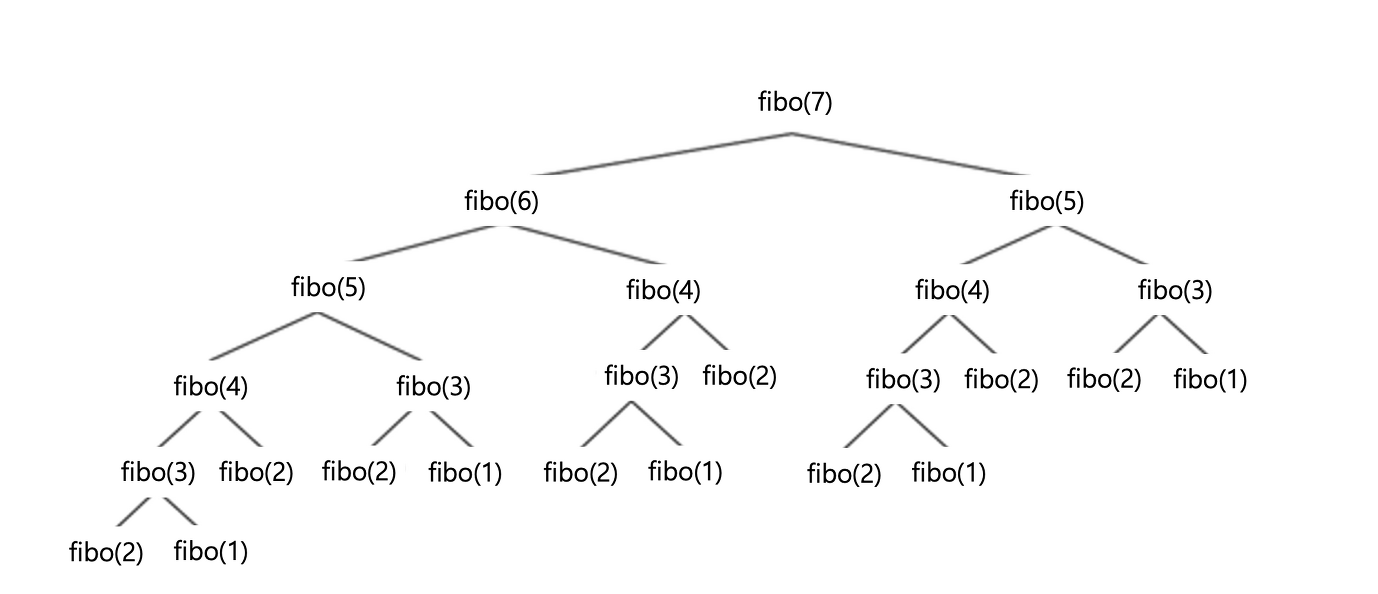
7번째 값을 구하기 위해서는 총 25번의 함수가 호출된다는 것을 알 수 있다. 이 과정에서 fibo(5), fibo(4), fibo(3)들이 이미 진행했던 연산임에도 불구하고 재귀되며 반복적으로 연산하는 것을 볼 수 있다.
이러한 반복적인 연산을 부분 반복 문제(Overlapping Subproblem) 이라고 한다. 이는 어떤 문제가 여러 개의 부분 문제로 쪼개질 수 있을 때 사용하는 용어이다.
이때 부분문제 (subproblem) 란 항상 새로운 부분 문제를 생성해내기 보다는 계속해서 같은 부분 문제가 여러번 재사용되거나 재귀 알고리즘을 통해 해결되는 문제를 가르킨다.
▶ 메모이제이션
큰 문제를 작은 문제로 나눌 수 있고, 작은 문제의 답을 모아 큰 문제를 해결할 수 있는 경우를 의미
최적 부분 구조란, 작은 부분 문제에서 구한 최적의 답으로 합쳐진 큰 문제의 최적의 답을 구할 수 있어야 한다는 것이다.
아래 피보나치 수열의 식을 보자.
fibo(n) = fibo(n-1) + fibo(n-2)큰 문제의 답인 fibo(n) 이 최적의 답이 되려면, 작은 부분의 문제인 fibo(n-1), fibo(n-2)이 최적의 답이어야만 한다. 작은 부분의 문제의 최적의 답으로 큰 문제의 최적의 답을 구한다는 뜻이다.
여기서, fibo(n-1)을 구하기 위해서는 다시 fibo(n-2) + fibo(n-3)이 되고, fibo(n-2)가 중복되게 된다. 그리고 최적 부분 구조를 만족한다면 문제의 크기에 상관없이 fibo(n-1)은 언제나 일정한 값을 가진다.
그럼 이 중복되는 연산과정을 줄이기 위해서는 어떻게 해야할까? 이것은 바로 Memoization 개념에서 설명할 수 있다.
탑다운(Top-Down) vs 바텀업(Bottom-Up)
▶ Top - Down 방법
말그대로, 위에서 아래로 접근하는 방법으로, 큰 문제에서 부분 문제로 쪼개가면서 재귀 호출을 통해 문제를 푸는 방법이다.
큰 문제를 해결하기 위해 작은 문제를 호출하는 방식
탑다운(메모이제이션) 방식은 '하향식'이라고도 한다.
점화식을 이해하기 쉬운 장점이 있다.
▶ Bottom - up 방법
말그대로, 아래서 위로 접근하는 방법으로 부분 문제에서부터 문제를 해결하여 점차 큰 문제를 풀어가는 방식이다. for 문을 이용하는 방식이 이에 해당한다.
가장 작은 문제들부터 답을 구해가며 전체 문제의 답을 찾는 방식
바텀업 방식은 '상향식'이라고도 한다.
재귀 호출을 하지 않기 때문에 시간과 메모리 사용량을 줄일 수 있는 장점이 있다.