LCS정의
최장 공통부분 수열은(LCS, Longest Common Subsequence) 여러 개의 수열이 주어졌을 때 두 수열의 부분 수열이 되는 수열 중 가장 긴 수열을 찾는 방법이다.
Subsequence의 뜻은 부분 수열 이라는 의미로 문자열이 연속적이지 않아도 된다는 의미이다.즉, 두 문자열 a, b를 비교할 때 공통 부분 수열 중 길이가 가장 긴 부분 수열을 의미한다.
문제링크
풀이방법
구하는 방법은 하나의 수열을 순서대로 다른 수열의 모든 문자와 비교하여 같은지 비교하는데, 동적 계획법(DP)을 활용하여 문제를 푼다.
- 만약 같다면 현재 비교하고 있는 [n][n] 번 위치의 문자 이전에 매치됐던 [n-1][n-1] 번 위치에 있는 문자에 더한다.
- 만약 다르다면 비교하기 이전에 나왔던 가장 긴 길이를 갖도록 하기 위해서 [n][n-1] 위치의 값과 [n-1][n] 위치의 값을 비교하여 큰 값을 가진다.
- 배열의 최종 위치의 숫자는 가장 긴 수열의 길이를 갖게 된다.
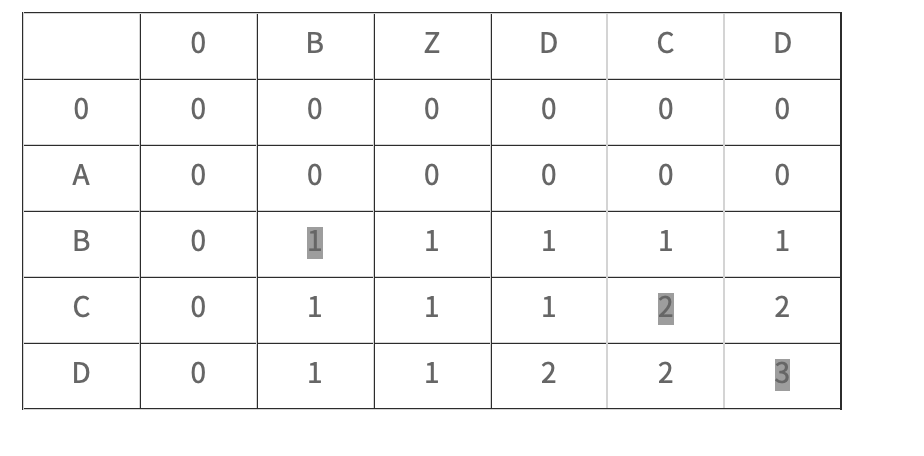
예시1: ABCD, BZDCD => BCD
예시: ABCD, BZDCD => BCD
예시에서 ABCD에서 B가 BZDCD에서 B와 매치됐을 때([2][1] 번 위치) A는 매치된 내용이 없기 때문에 1이 되고 ABCD의 C가 매치될 때는 B([2][1] 번 위치)에서 매치된 내용이 있기 때문에 2가 된다.
예시에서 ABCD의 B가 BZDCD의 Z와 비교할 때 매치하지 않기 때문에 [1][2] 번 위치와 [2][1] 번 위치의 값을 비교하여 큰 값인 1이 된다.
아래는 비교가 끝난 배열이다.
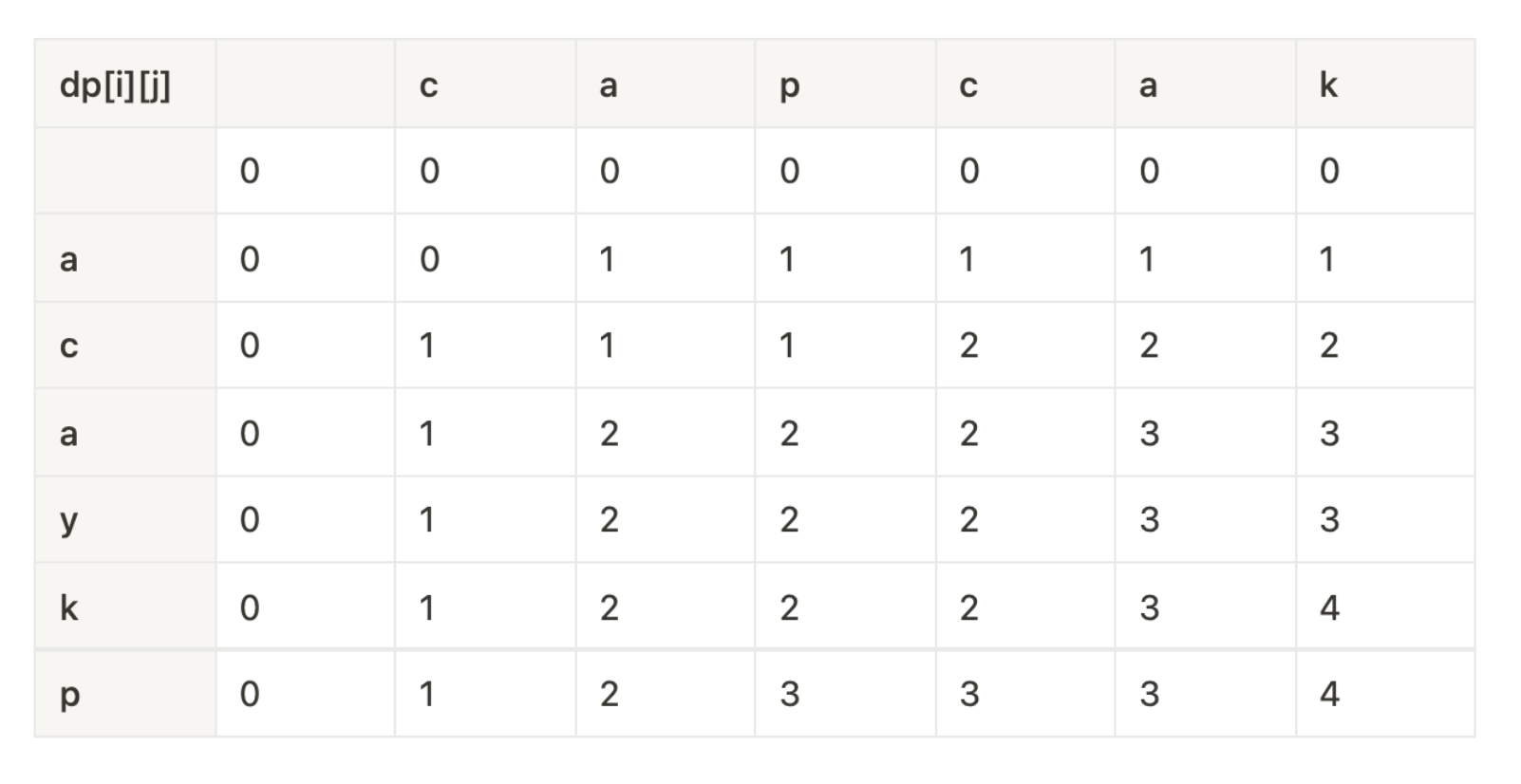
예1 ACAYKP, CAPCAK => ACAK
점화식을 통해 다시 설명해보자.
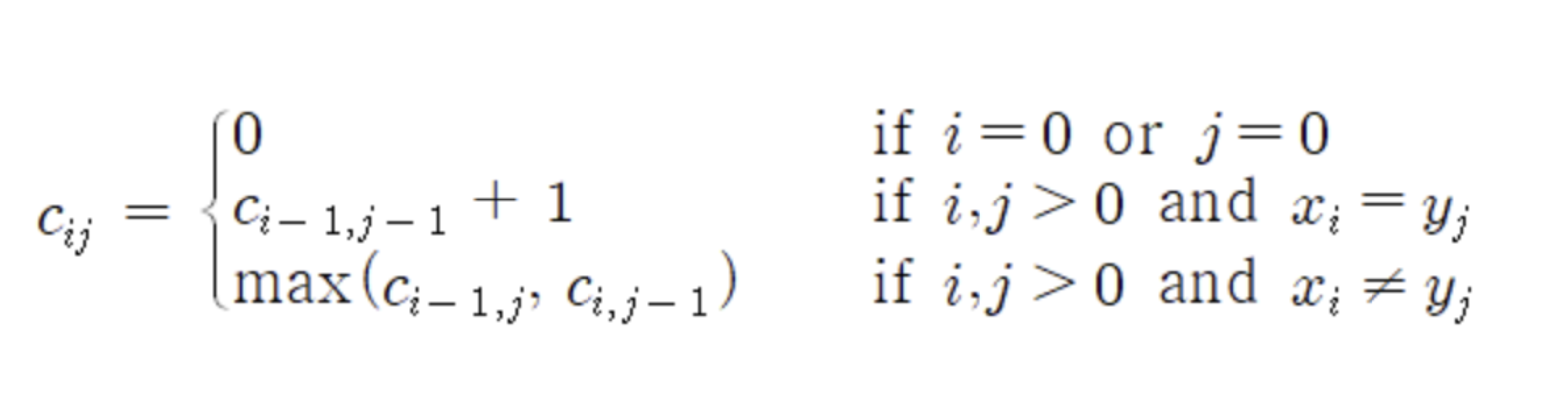
if (i == 0 or j == 0)일 경우 겹치는 문자가 존재하지 않기 때문에 0이다.
i, j > 0이면서 x(i)=y(j)로 문자가 겹친다면, c[i][j] = c[i - 1][j - 1]+1 이다.
i, j > 0 이면서 x(i)!=y(j)로 문자가 겹치지 않는다면, c[i][j] = max(c[i - 1][j], c[i][j-1])이다.
따라서 구하고자 하는 LCS의 길이는 가장 오른쪽 아래의 dp[6][6] = 4이다.
이 점화식을 코드로 나타내면 다음과 같다.
for (int i = 1; i <= aLen; i++) {
for (int j = 1; j <= bLen; j++) {
if (a[i-1] == b[j-1])
lcs[i][j] = lcs[i - 1][j - 1] + 1;
else lcs[i][j] = Math.max(lcs[i][j - 1], lcs[i - 1][j]);
}
}만약, LCS가 무엇인지 알고 싶다면 어떻게 해야 할까?
역추적(Back Tracking)을 이용해서 구하면 된다.
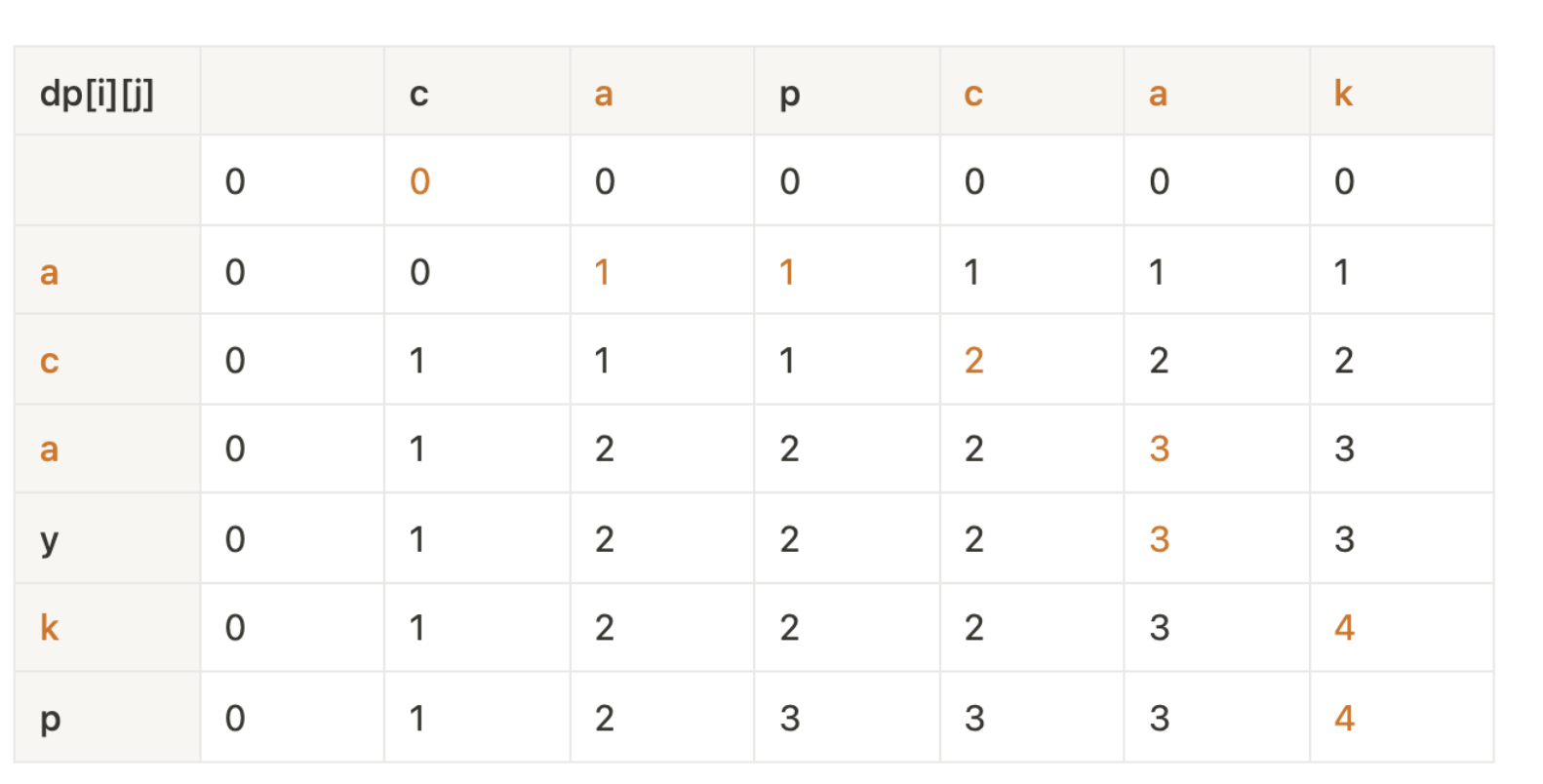
위의 주황색으로 표시된 내용을 보면,
dp[6][6]을 보았을 때 어떤 경로를 통해서 왔는지 역추적으로 출발 지점을 따라가면 된다.
a[i]==b[j]라면 dp[i-1][j-1]의 위치로 이동하면 되고, 그렇지 않다면 dp[i-1][j] dp[i][j-1]중에 큰 값으로 이동하면 된다.