행렬경로문제
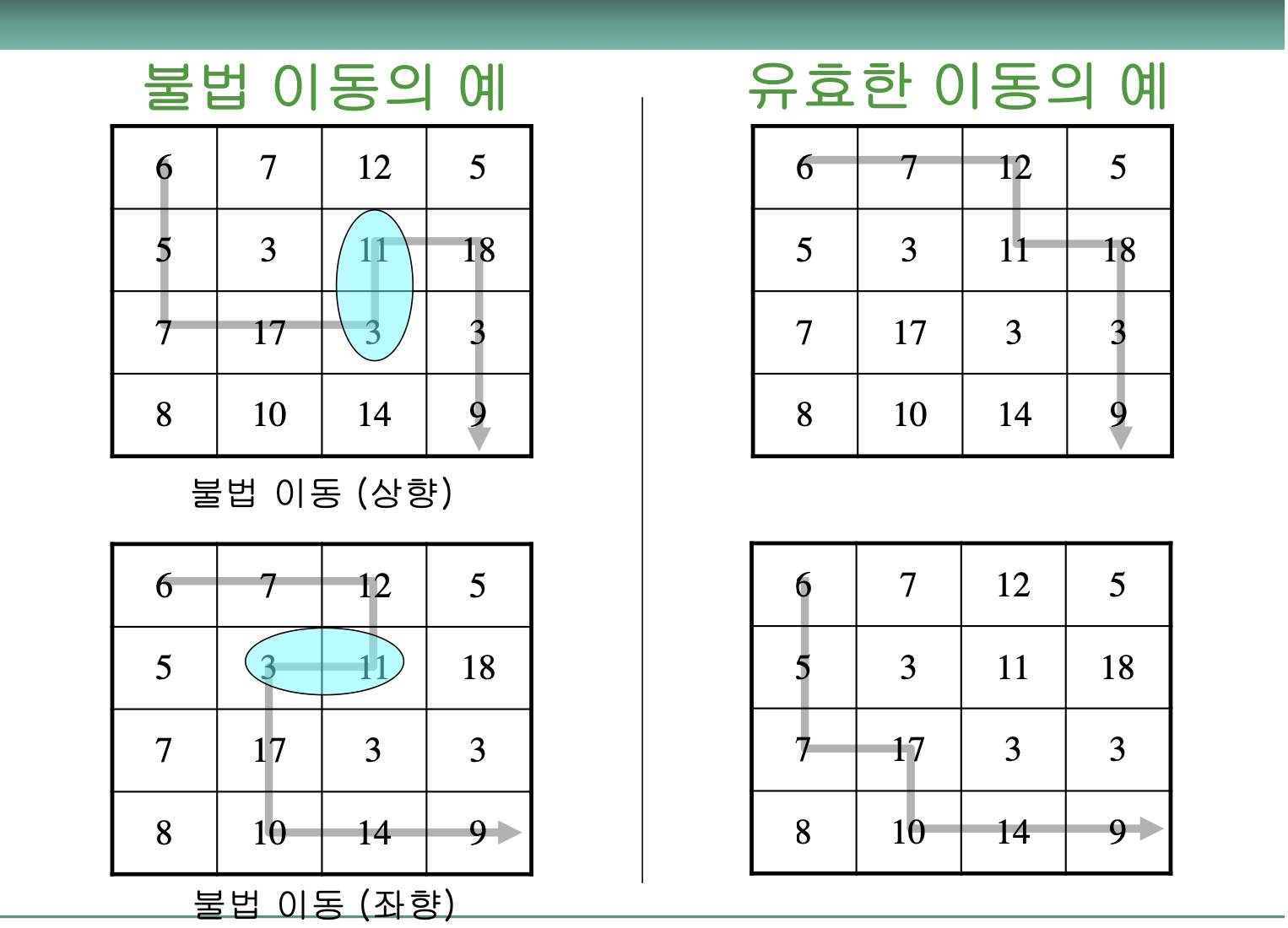
양수 원소들로 구성된 n×n 행렬이 주어지고, 행렬의 좌상 단에서 시작하여 우하단까지 이동한다
• 이동 방법 (제약조건)
– 오른쪽이나 아래쪽으로만 이동할 수 있다
– 왼쪽, 위쪽, 대각선 이동은 허용하지 않는다
• 목표: 행렬의 좌상단(1, 1)에서 시작하여 우하단(n, n)까지 이동하는 모든 경로의 값 중 가장 높은 값을 구한다.
다이나믹 프로그래밍 조건
• 원소(i,j)에도달하기직전의원소 – 원소 (i-1, j)와 (i, j-1)
– 원소 (i, j)는 무조건 방문
• 점수가 높은 경로
– (i-1, j) ~ (i, j) 경로와 (i, j-1) ~ (i, j) 경로 중 점수가 높은 것을 채택
• (1, 1)~(i, j)에 도달하는 최고점수는?
– max{ (i-1, j)의 점수, (i, j-1)의 점수 } + (i, j)의 점수
• 문제 (I, j)의 최적해는 (i-1, j)의 최적해와 (i, j-1)의 최적해로 설명 가능
⬇
최적부분구조충족
다이나믹 프로그래밍 조건
• Cij -원소(1,1)에서(i,j)에이르는최고점수 • mij –행렬원소(i,j)의값
0 if i=0 or j=0 mij + max{Ci, j-1, Ci-1, j} otherwise
• Cij는 원소 Ci,j-1,Ci-1,j의 재귀적 관계로 표현 가능
⬇
최적부분구조충족
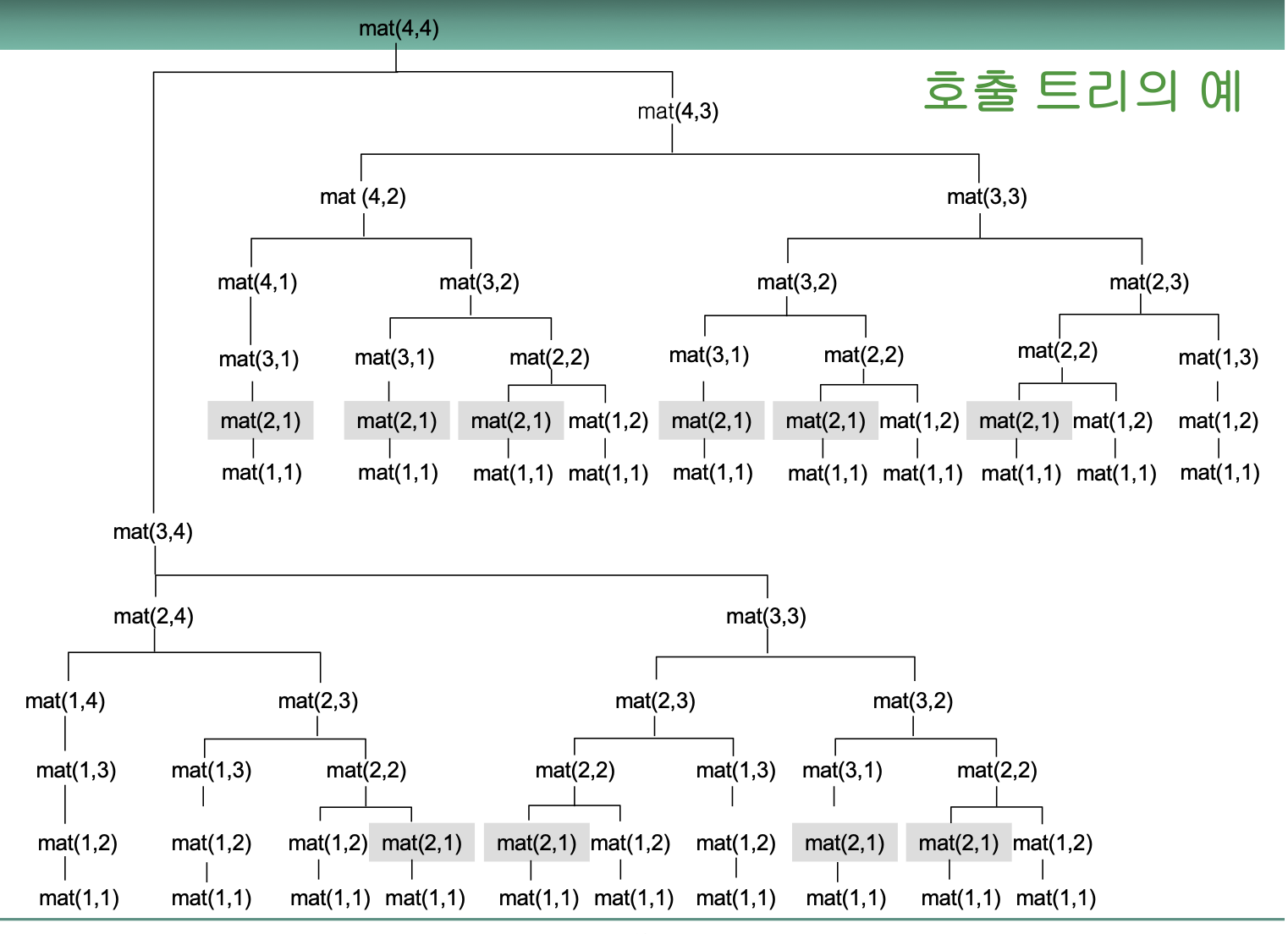
재귀 알고리즘
matrixPath(i, j)
▷ (i, j)에 이르는 최고점수 {
if (i = 0 or j = 0) then return 0;
else return (mij + (max(matrixPath(i-1, j), matrixPath(i, j-1)))); }
Time Complexity: O(n*n) = O(n2)
⬇
행렬의 크기가 커질 수록 중복 호출이 매우 큰 횟수 발생