What is ML?

ML(Machine Learning)이란, data로부터 pattern을 학습하는 것을 말한다.
즉, explicit programming이 들어가지 않고 pattern을 배운 function이 prediction(decision)을 output을 뱉어낸다.

$f_θ:X→Y$, 이는 X의 원소 집합들을 Y로 mapping 시키는 역할을 하는 함수 f를 의미한다. $θ$는 $X→Y$로 mapping시킬 수 있는 parameterized function을 일컫는다.
정리하자면, X는 Data Y는 Target인데 이를 $f$를 이용한다.

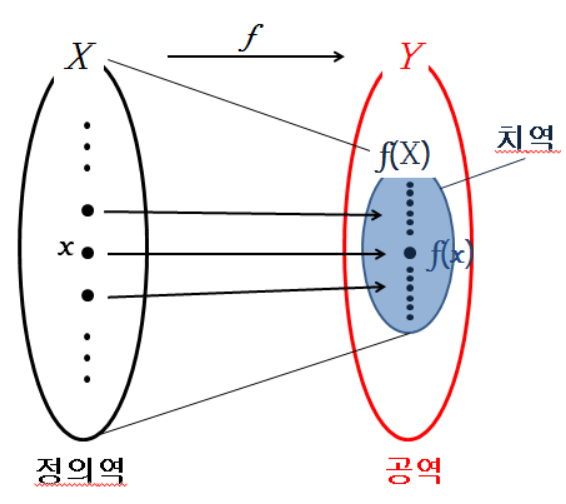
우리가 잊지 말아야할 것은, $f$는 function이기 때문에 이를 수학적으로 생각해보면 X의 element는 Y값에 1개씩만 mapping이 되어야한다는 것을 잊지말자, 위 그림은 우리가 중학교때 배웠던 함수를 쉽게 이해할 수 있는 함수 정의 그림이다.

아무튼, ML의 최종 목표는 $f_θ$에서 $θ$를 잘 찾는 것이 목표이다.
즉, 최적의 parameter인 $θ^*$를 찾는 것이 목표이다.

$\theta^* = \arg\min_\theta E_{(x,y) \sim P(x,y)}[L(f_\theta(x),y)]$

$\theta^*$를 찾는 식은 위와 같으며, 확률 분포 $P(x,y)$가 있을 때 sampling 값 $(x,y)$를 추출하여 그것에 대한 기댓값을 구하여 $L(Loss Function)$이 $y(target)$값과 $f_{\theta}(prediction)$값의 차이를 최소화하는 것을 의미한다.

Definition by Tom Mitchell
A computer program is said to learn from experience E with respect to some class of tasks T, and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E

---

Set Notation

DL과 ML은 모두 수학적 모델 기반이기 때문에 수학적 기호를 간단히 정리해봅니다.

• $∝$: 비례 관계, $y=ax$이면 $y∝x$

• $\triangleq$: 정의, $f(x) \triangleq ax$: 왼쪽 항을 오른쪽 항에 정의

• $Z_+$: 정수 집합(The Positive Integer)

• $R$: 실수 집합(The Real Number)

• $R_+$: R에서 양수 집합(The Positive reals)

• $\approx$: 근삿값(Approximately Equal)

• $\{1, ..., N\}$: 유한 집합(The finite set)

• $A⊆B$: A는 B에 부분집합 혹은 동일

• $X \in A$: X는 A에 속하는 원소

• $\prod_{i=1}^n x_i$: product of $x_i$ from i=1 to n

• $\lfloor x \rfloor$: 내림(Floor of X)

• $\lceil x \rceil$: 올림(Ceiling of X)

• $\neg A$: logical not(a가 True이면, $\neg a$는 False)

• $|A|$: A집합의 element 개수(size of set A)

• $A \land B$: AND 기호

• $A \lor B$: OR 기호

• $\mathbf{a} \circ \mathbf{b}$: 벡터 내적(Elementwise Product of Vectors)

• $\mathbf{a} \ast \mathbf{b}$: 벡터 컨볼루션(Convolution of Vectors)

• Vectors: x$=[x_1,...,x_D]^T\in R^D$, x가 소문자이고 bold면 vector

• Matrices: X$\in R^{N \times D}$

• Set Notation: $D=\{(x_n, y_n)\}^N_{n=1}$

---

Key Terminology

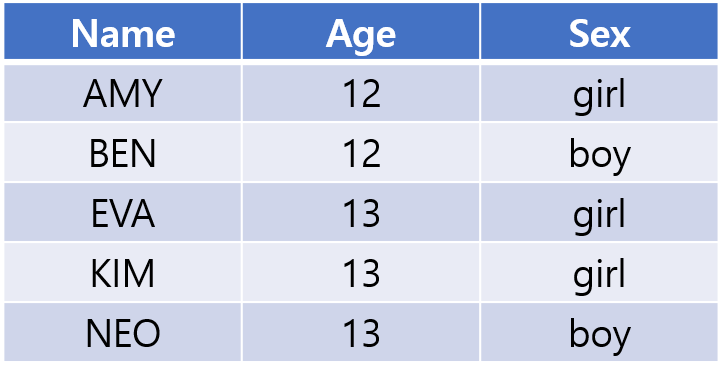
위 데이터프레임에서 우리는 ML의 data의 terminology 용어인 sample, variable, feature, target/label, dataset을 알 수 있다.

Sample이란, 1개의 행 값 또는 data point를 의미하는데, $[AMY, 12, girl]$이 1개의 Sample이라고 볼 수 있다.

Variable이란, Sample이 가지고 있는 속성을 이야기하는데 위 데이터프레임에서는 Name, Age, Sex가 될 수 있다. 논문을 읽다보면 variable과 feature은 거의 동일한 말이기도 하다.

Target이란, 위 데이터프레임에서 $[Name, Age]$를 모델 $f$에 넣어 $[Sex]$를 예측하려는 모델이 있다고 하자, 그러면 데이터프레임에 나와있는 $[Sex]$가 target이며 $[Name, Age]$를 학습하고 prediction을 한 값은 prediction value로 되는 것이다. 앞에서 말했듯, target과 prediction값의 차이를 줄이는 것이 ML의 목표이다.

Dataset이란, 위 데이터프레임 전체를 이야기하며 sample의 set이다.

우리는 위 데이터프레임의 형태가 행렬과 유사하다는 것을 알 수 있는데, 각 값을 numerical value로 transform시켜 vectorization을 시킬 수 있다.
자연어처리에서 각 단어를 vectorization하는 것과 같다.

---

Types of Data

Data의 형태는 Order vs Un-Ordered, Discrete vs Continuous, Binary vs Non-Binary로 구별할 수 있다.

• Categorical(Nominal) Data: Discrete, Un-Ordered categories; EX) Color(Red, Blue, Green)

• Ordinal Data: Discrete, Ordered categories; EX) Education Level(High School, Bachelor's, Master's, Ph.D)

• Numerical Data: Continous(Real Number) or Discrete(Integer) numerical values; EX) Height, Weight, Age

• Binary Data: Special case of categorical with two categories EX) YES/NO, True/False, 1/0

---

Prediction Tasks

ML에서 label의 형태에 따라 task가 정해지게 된다.
크게 Classification(분류), Regression(회귀), Clustering(그룹화)가 있다.

• Classification: Predicting a categorical label

• Regression: Predicting a continuous numerical value

• Clustering: Grouping similar samples, unsupervised

---

Models and Parameters

Linear Regression(선형 회귀)를 예시를 들자면,

$f(B) = B_0 + B_1x_1 + B_2x_2 + ... + B_px_p + ε$

위 식에서 $B_0 \sim B_p$는 parameters, $x_1 \sim x_p$는 features이다.
그렇다면 $B$값을 조정할 수 있으며 $x$는 constant이니 값을 조정할 수 없다.

따라서, 우리는 feature의 coefficient(parameter)를 통해서 해당 feature의 가중치를 곱하는 꼴로 어느 output을 도출하는데 어떤 feature가 가장 중요한지 알 수 있으며 decision map 혹은 decision boundary이 어디인지 시각화가 가능할 수 있다.

---

Decision Tree

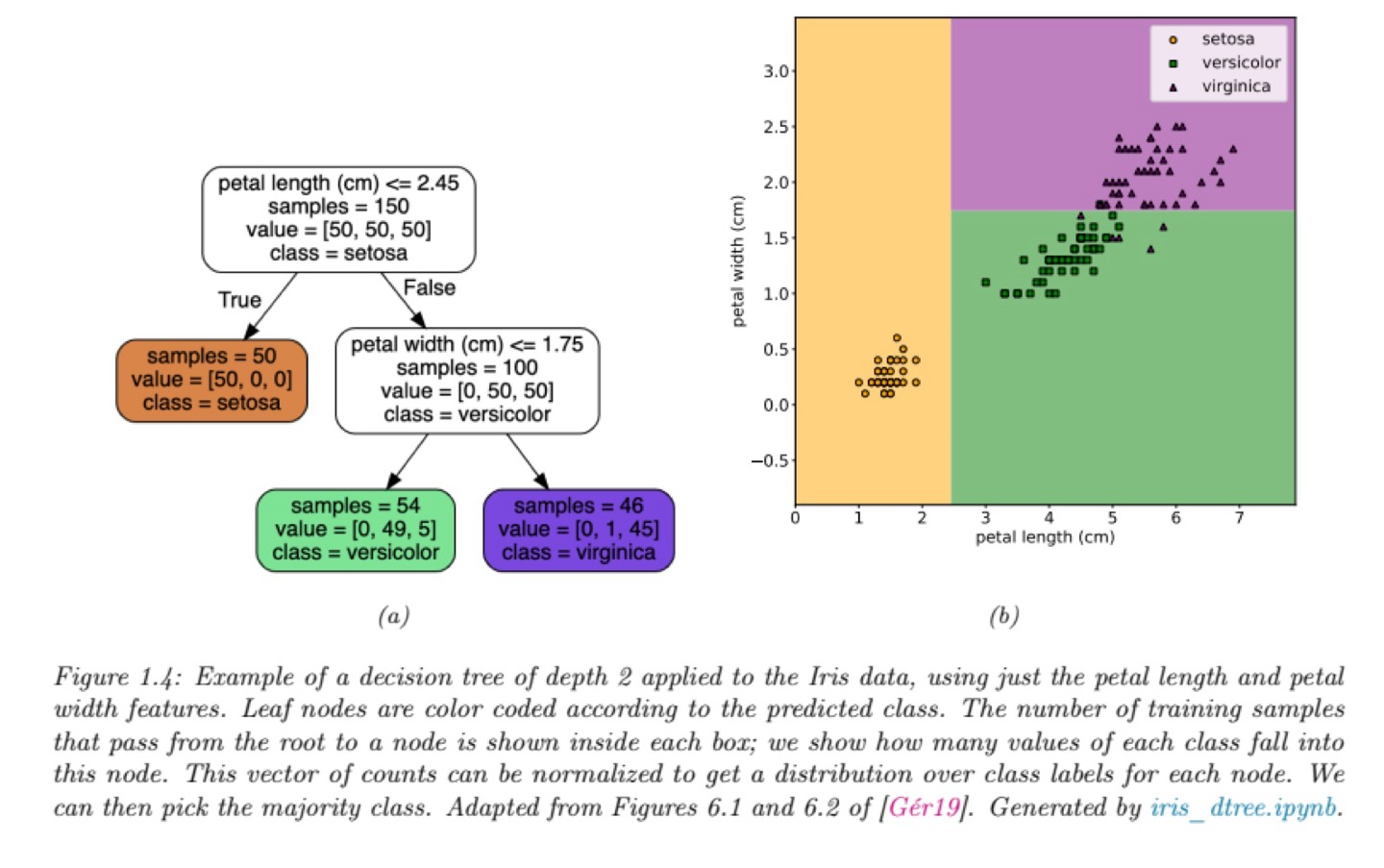
Decision Tree는 $D=\{(x_n, y_n)\}^N_{n=1}$를 학습하여 최적의 decision boundary를 세우는 것이 목표이다.
그렇다면 decision boundary를 나누는 것은 parameter에 의해서 정해지게 되는데, 위 그림에서는 [Petal length, Petal height]의 feature만을 이용한다.

Empirical Risk Minimization

우리의 최종 목표는 decision boundary를 최적의 parameter인 $\theta^*$를 찾는 것인데, 이에 대한 loss function도 잘 정해야한다.

그렇다면, 가장 단순하게 생각할 수 있는 Missclassification rate로 loss를 정의할 수 있다.

$L(\theta)=\frac{1}{N}\sum^N_{n=1}I(y_n≠f(x_n;\theta))$ where, $I(e)$= $1$ if $e$ is true else $0$

위 식에서 $I$는 indicator function으로 정의된 것을 본다면 step function이다.
이는 오류가 발생한다면 cost값을 1만 주기 때문에 feature마다의 중요도를 알기 어렵기 때문에 우리는 각 feature마다의 cost를 달리 줄 필요가 있다.

Asymmetric Loss Function

따라서, 우리는 feature마다 혹은 label마다 중요도가 다 다르기 때문에 특정 오차를 중요하게 봐야할 수 있다.
그래서 asymmetric loss를 사용하여 어떠한 값에다가 loss를 크게주게 되는데, 이 역시 어떤 한 label값에 편향이 주어지기 때문에 unbalance하다는 문제점이 있다.

정리하자면,
우리는 train data를 통해 inference를 하게 된다.
하지만, 통계학에서 표본을 통해 모집단을 정확하게 예측하는 것은 불가능한 것과 같이 test data가 모집단이라면 이는 100%의 성능을 기대하기는 어렵다.
현재까지의 기술로만 보아도 100%의 성능이 나와있는 것은 찾아보기 힘들다.

따라서, 우리는 불확실성 즉 Uncertainty를 알아내는 것이 중요한데 이를 conditional probability distribution을 사용하는 것이 대표적이다. ; $p(y=c|x;\theta)=f_c(x;\theta)$

---

Logistic Regression

이를 설명하기 전에 softmax-function과 linear function에 대해 먼저 알고 넘어가보자

Softmax-Function

여러 개의 class가 존재할 때, 우리는 각각의 class의 numerical value값을 확률값으로 변환시킬 수 있다.
이는 대표적으로 softmax-function을 이용하며 정의는 다음과 같다.

$softmax(a) \triangleq [\frac{e^{a_1}}{\sum^N_{c'=1}e^a_{c'}}, ..., \frac{e^{a_C}}{\sum^N_{c'=1}e^a_{c'}}]$ , $R^C(Real)$에서 $[0,1]^C(Prob)$으로 변환시킨다.

Linear Function

앞에서 단순 선형 회귀(Linear Regression)에 대해서 설명했는데, 상당 부분 비슷하지만 이를 vector로 표현해보면 다음과 같다.

$\hat w^T \hat x = b + w^Tx$로 bias term을 $\hat w^T$로 absorb할 수 있다.
이를, $f(x; w)=w^Tx$로 나타낼 수 있다.

Maximum Likelihood Estimation

위와같이 binary classification을 한다고 해보면, 일반적으로 True값을 1, False값을 0으로 할당해준다.

$\prod_{i=1}^np(y_i|x_i;\theta)=\prod_{i=1}^nM^{y^{(i)}}\times(1-M)^{1-y^{(i)}}$

M은 확률 값으로 바꿔주는 softmax function 혹은 sigmoid function이 될 수 있겠다.

pytorch를 쓰신분들은 아시겠지만, classification에서 one-hot-encoding을 사용하는 이유가 label값의 수학적 trick을 이용한 것이다.

따라서, 위의 식은 오로지 True값만을 맞출 확률로 정의할 수 있다. 하지만 위는 다량의 데이터가 있다면 계산이 대단히 복잡해진다는 단점이 있다.
한마디로 비효율적이라는 이야기이다.

따라서, 우리는 log scale로 변환하여 log의 성질을 이용하게 된다.

$\sum^n_{i=1}y^{(i)}log(M)+(1-y^{(i)})log(1-M)$

log의 성질을 이용하면 덧셈 및 지수를 계수로 꺼내올 수 있다.
모든 곱하기 연산을 덧셈으로 바꾸어 계산식이 훨씬 편해진 것과 더불어 특히 underflow가 나지 않는다는 장점이 존재한다.

그래서, 우리는 위와 같은 식을 loss function으로 사용하게 된다면 $L(y,f(x;\theta))=-log\ p(y|f(x;\theta))$

loss function은 대체로 minimization하는 것이 목표이기 때문에 음수를 붙여줘야한다.

이를 Maximum likelihood estimate(MLE) 이라하며,
$\hat \theta_{mle}=arg min_{\theta}NLL(\theta)$가 되는 것이다.
이때의 NLL은 $L(y,f(x;\theta))$이가 된다.

---

Regression

여기서도 마찬가지로, regression에서 사용하는 loss function에 대해 알아보겠습니다.

Gaussian Distribution for Regression

Gaussian function의 정의는 다음과 같다.
$N(y|u,σ)\triangleq \frac{1}{\sqrt{(2\pi σ^2)}}e^{\frac{-1}{2σ^2}(y-u)^2 }$

일반적으로 분포는 가우시안 분포를 따르게 되는데, 회귀 모델을 모델링할때도 가우시안분포를 가정한다.
이는 잔차(target-predict)값이 가우시안 분포를 띈다고 가정한다는 말이다.

따라서 위의 식도 MLE와 같이 log scale변환을 해주게 된다면 MSE가 남게 된다.

log scale변환은 알아서 해보시고,, 결국 남는 값은 $\frac{1}{2σ^2}MSE(\theta)+const$ 이다.

결론은, 가우시안을 가정해서 회귀 문제를 풀게되면 이는 MSE를 최소화하는 것과 같게 되는 것이다.

---

Polynomial Regression

Polynomial Regression은 다중 회귀라고 해석이 되는데, 이는 앞에서 보았던 선형 회귀의 확장이다.

$f(x;w)=w^TΦ(x)\ ,where\ Φ(x)=[1,x,x^2...,x^D]$

이는 원래 있던 data를 뻥튀기해서 가상의 변수(feature)를 만듬으로써 다차원적으로 feature와 target값이 관계가 있다고 가정하는 것이다.
이는 모델의 complexity를 올리는 방법으로, 선형 회귀는 오로지 1차원적인 관계만 찾았었는데 이는 사용자가 정의한 차수까지 정의하여 더욱 복잡한 관계식을 알아낼 수 있다.

parameter가 여전히 linear하기 때문에, parameter에 대한 식으로 linearity를 이용 가능하다고 하는데,, 이를 잘 이해하지못해서 댓글로 알려주시면 정말 감사하겠습니다..

아무튼, 위와 같이 가상의 변수를 만드는 과정이 feature engineering이라고 하는데 이는 인간의 직관이나 원래 알고 있는 사전 정보를 이용해서 모델의 성능을 올리는 과정이다.

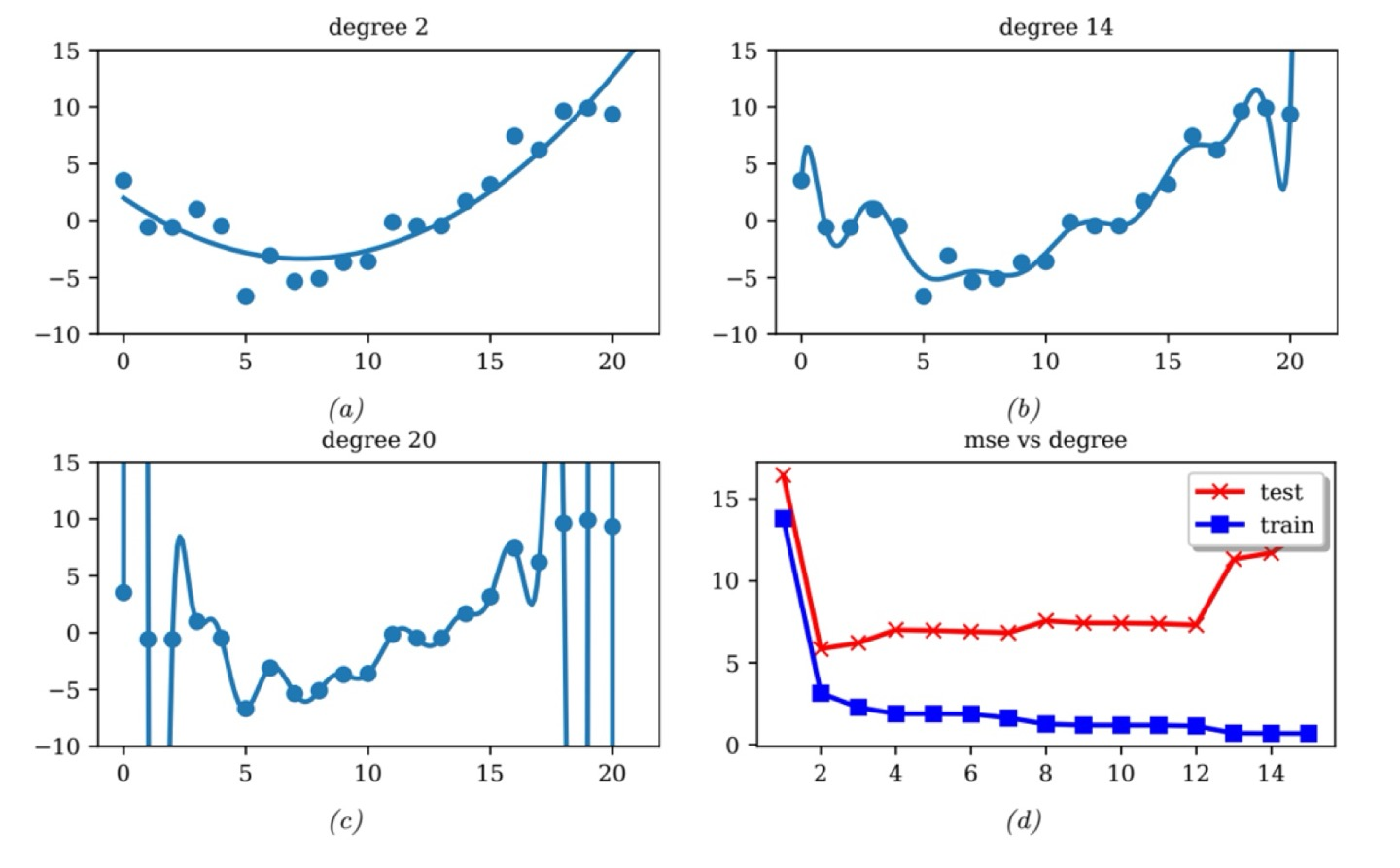
$Φ(x)=[1,x,x^2...,x^D]$와 같이 단순히 거듭제곱을 이용하는 것이 아닌 $sin(x), log(x)$ 로 feature engineering을 할 수 있습니다.

Multidimensional Regression

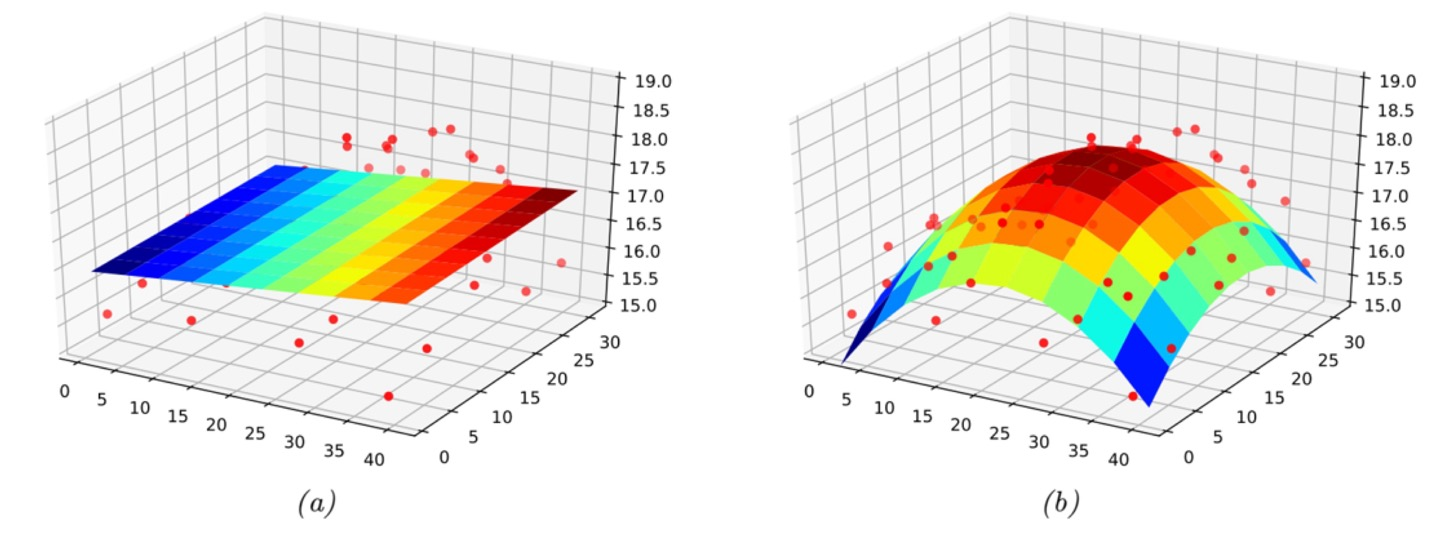
(a)는 $f(x;w)=w_0+w_1x_1+w_2x_2$의 3차원 선형 방정식, (b)는 $f(x;w)=w_0+w_1x_1+w_2x_2+w_3x_1^2+w_4x_2^2$으로 (a)에서 각 $x_n$에 대해 나름의 feature engineering을 적용하였다.
(a)와 (b)는 모두 $x_1, x_2$에 관한 방정식으로 되어있으며 w는 x에 대한 coefficient이다.

(a)는 단순 선형 방정방정식이기 때문에 평면이 decision plane이 적합하지 않은 것을 볼 수 있다.
반면, (b)는 (a)와 비교해서 decision plane을 잘 설명함으로써 (a)보다 loss가 낮을 수 있다는 것을 짐작할 수 있다.

따라서 위의 그래프처럼, decision plane을 만들기 전 feature를 보고 decision plane을 잘 만들기 위한 feature engineering을 하기 위해 empirical experiment가 중요하다고 볼 수 있다.

---

Overfitting and Generalization

앞에서, 우리는 아무리 많은 dataset을 가지고 있어도 모집단을 완벽하게 예측할 수 없다.
이를 Population Risk라 하는데, 이를 식으로 $L(\theta,p^*)\triangleq E_{p*(x,y)}[L(y,f(x;\theta)]$이다.
$p^*(x,y)$는 실제 (x,y)의 distribution으로, 모집단 dataset의 distribution이다.

만약, 모집단을 완벽하게 예측할 수 있다면 $L(\theta, p^*)-L(\theta;D_{train})$으로 generalization gap인 loss을 이용할 수 있을 것이다.
하지만, 이는 실제로 계산이 불가능하며, dataset은 한정적이기 때문에 제한된 sample data로만 접근해야하는 것이 한계점인 것은 분명하다.

그래서 dataset 자체를 3개로 split하게 되는데, 이를 train, validation, test로 나누어 train dataset으로 학습한 뒤 validation과 test로 모델의 성능 평가 및 parameter를 조절하는 것에 사용한다.

최근 들어, all-in-one DL model이 개발되고 있지만 아직까지 model의 완성도가 높지 않다고 한다.
따라서, conventional DL model은 dataset에 따라서 model을 선별해야한다.

George Box
"All models are wrong, but some models are useful"

실제로 image classification의 task를 수행하는 Vision Transformer는 transformer의 architecture를 최대한 유지한 채 학습하려고 노력했다.
그 전에는 inductive bias로 computer vision의 breakthrough를 잘 찾지 못했다.

하지만 vision transformer는 inductive bias를 해결한 대표적인 사례로, 현재는 computer vision에 transformer가 많이 이용되고 있다.

Inductive Bias: assumptions that work well in one domain may not in another

---

Discovering Latent "Factors of Variation"

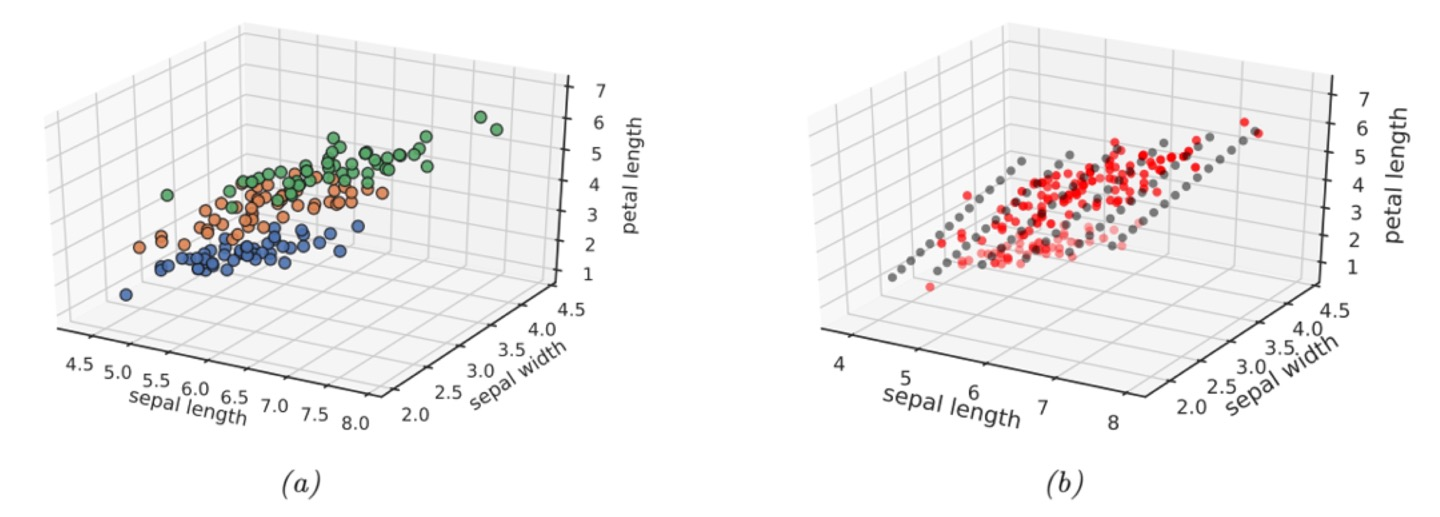
이 부분은, data의 차원을 줄여 data의 본질(essence)를 찾는 것을 목표로 한다.

증명사진이 있다고 하자
직관적으로, 증명사진에서 가장 중요한 부분은 "이목구비"일 것이다.
하지만 이목구비를 제외한 나머지 pixel 혹은 data는 많은 dimension을 사진에서 차지하고 있다.
따라서, 이를 차원 축소를 통해서 latent factor를 찾는 것이 목표인데 여기서의 latent factor는 이목구비가 되는 것으로 data의 차원을 줄이되 핵심적인 부분은 잘 보존할 수 있는 것이다.
그래서 High-dimension은 low-dimension에서 파생되어 관측이 된 것이라고 할 수 있다.

대표적인 기법은 PCA가 있다.