Signals

동굴에서 사는 박쥐는 초음파를 통해서 주변의 사물을 인지하는 능력을 가졌다.
우리는 여기서 박쥐가 가지고 있는 초음파를 input signal이라고 볼 수 있으며, 동굴에서 초음파를 가공하게 된다면(system), 이를 output signal이라고 부를 수 있다.

그림을 표현하면 아래와 같다.

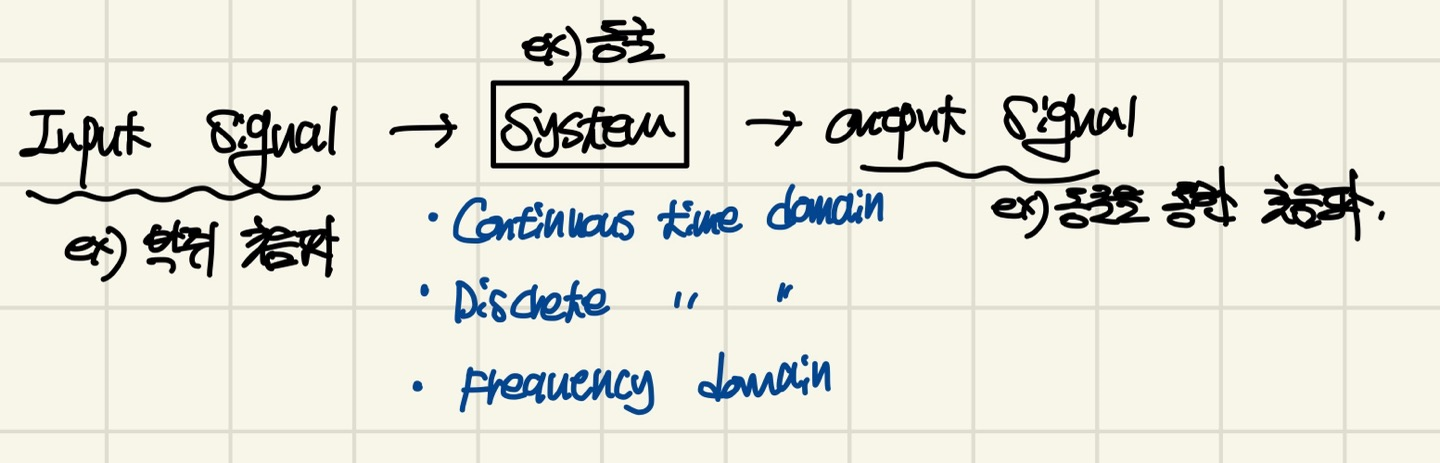
우리는 이러한 signal을 3가지의 domain을 통해서 분석 할 수 있는데 크게 3가지로 나뉘게 된다.

• Continuous time domain

• Discrete time domain

• Frequency domain

서로 다른 signal을 다른 domain으로 분석하게 된다면 processing 및 analysis를 보다 더 잘할 수 있게 된다. (3가지는 이후 포스트에서 깊게 다룹니다.)

Euler's formula

오일러 법칙의 식은 다음과 같다.

$e^{jx} = cos(x) + jsin(x)$

이 오일러 법칙은 초월함수를 다항함수의 합으로 표현할 수 있는 테일러급수로 표현이 가능하다.

$f(x) = C_0 + C_1X + ... + C_nX^n$, 이는 어떠한 f(x)를 우항의 다항식을 통해서 f(x)를 표현하는 방법으로 근사화한 함수라고 생각하면 된다.
만약, 정말 많은 차수까지 쓰게 된다면 f(x)와 같아지게 된다.

이때, coefficient를 구하는 것이 핵심인데 구하는 방법은 X = 0(맥클로린 급수)를 대입하면 구할 수 있으며 고계도함수도 이용해주면 구할 수 있다.

$f(0)=C_0, f'(0) = C_1, f''(0) = 2C_2, f'''(0) = 3!C_3$가 되게 된다.

그렇다면 $Cos(x)$를 맥클로린 급수를 이용해서 다항식으로 근사화해보자.

$f(x) = cos(x)$
$f(0) = 1, f'(0) = 0, f''(0) = 2C_2$가 된다.
$f''(0) = -cos(0)$이니, $C_2 = \frac{-1}{2}$이 된다.
어쨋든, 2차까지 근사화해보면, $f(x) = 1 - \frac{-1}{2}x^2$이 된다.

위와 똑같이 오일러 법칙도 맥클로린 급수를 통해서 유도할 수 있는데, 다음과 같다.

$f(x) = e^{jx}$
$f(0) = 1, f'(0)=j, f''(0)=\frac{-1}{2}, f'''(0)=\frac{-j}{3!}, f^{(4)}=\frac{1}{4!}, f^{(5)}=\frac{-j}{5!}$이 된다.
그렇다면, $f(x) = 1+jx-\frac{1}{2}x^2-\frac{j}{3!}x^3+\frac{1}{4!}x^4-\frac{j}{5!}x^5+...$로 표현이 된다.
이를 $sin(x)$와 $cos(x)$를 통해 표현할 수 있는데(위에서 cos을 맥클로릭 급수로 나타낸 것 처럼 sin도 표현 가능하다) $f(x) = cos(x)+jsin(x)$로 나타낼 수 있게 된다.

이러한 오일러법칙은 복소평면에 나타내어 본다면 다음과 같다.

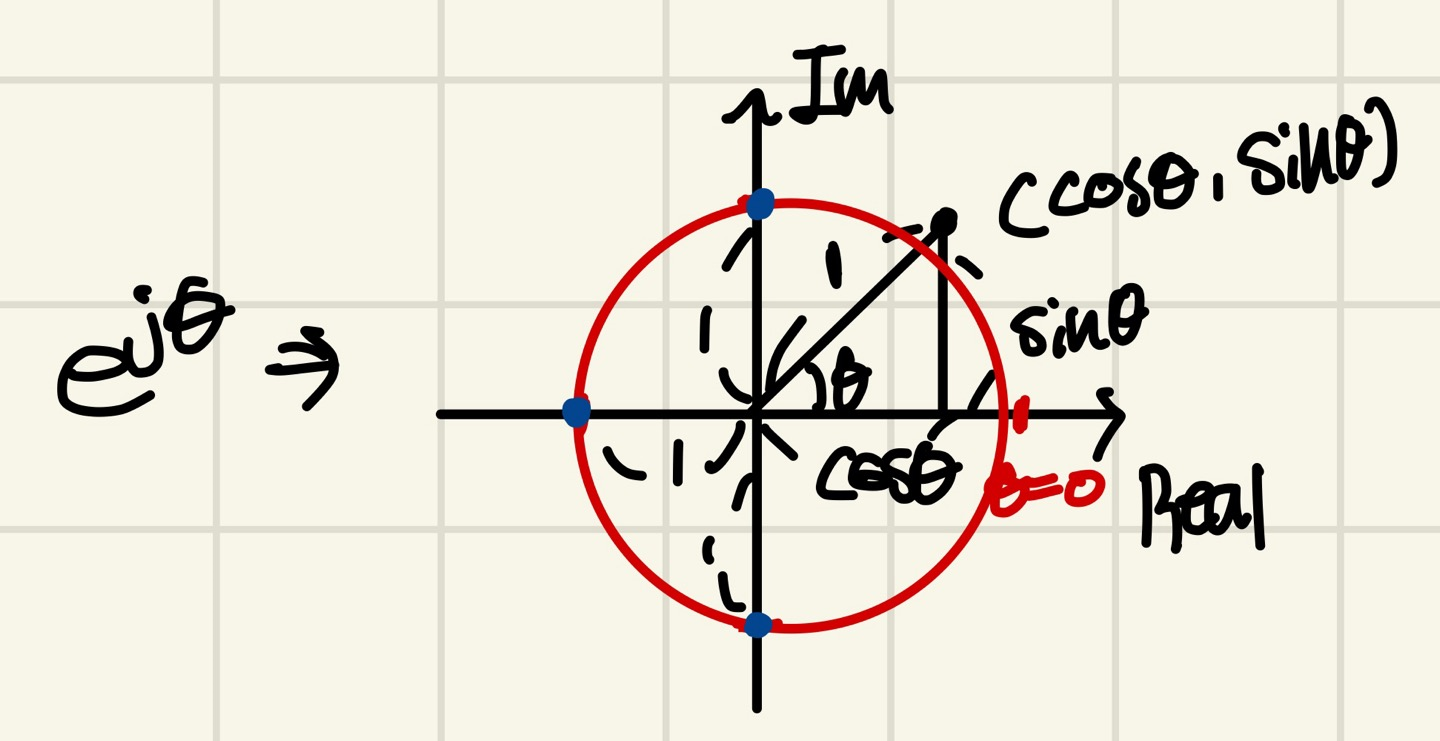
세타는 x로 표현하였습니다.

빗변의 길이가 1로 놓게 된다면, 이는 삼각형의 오른쪽 상단의 좌표는 $(cos(x), sin(x))$로 나타낼 수 있으며 $X=0$이라면 $(1, 0)$으로 표현할 수 있을 것이다.

만약 0~2𝝅까지 표현된다면, 빨간색과 같은 원을 하나 그릴 수 있게 된다.

원의 반지름은 $Ae^{jx}$에서 A가 된다.

만약, A>0이며 X가 0~2𝝅까지 표현할 수 있으면 위의 복소평면을 모두 나타낼 수 있게 되는데 이는 오일러 법칙, 즉 $e^{jx}$가 모든 수를 표현할 수 있다는 것을 알게 된다.