LTI System

LTI란, Linear Time Invariant로 Linear과 Time Invariant의 성질 2가지를 가지고 있다고 보면 된다.

Linear

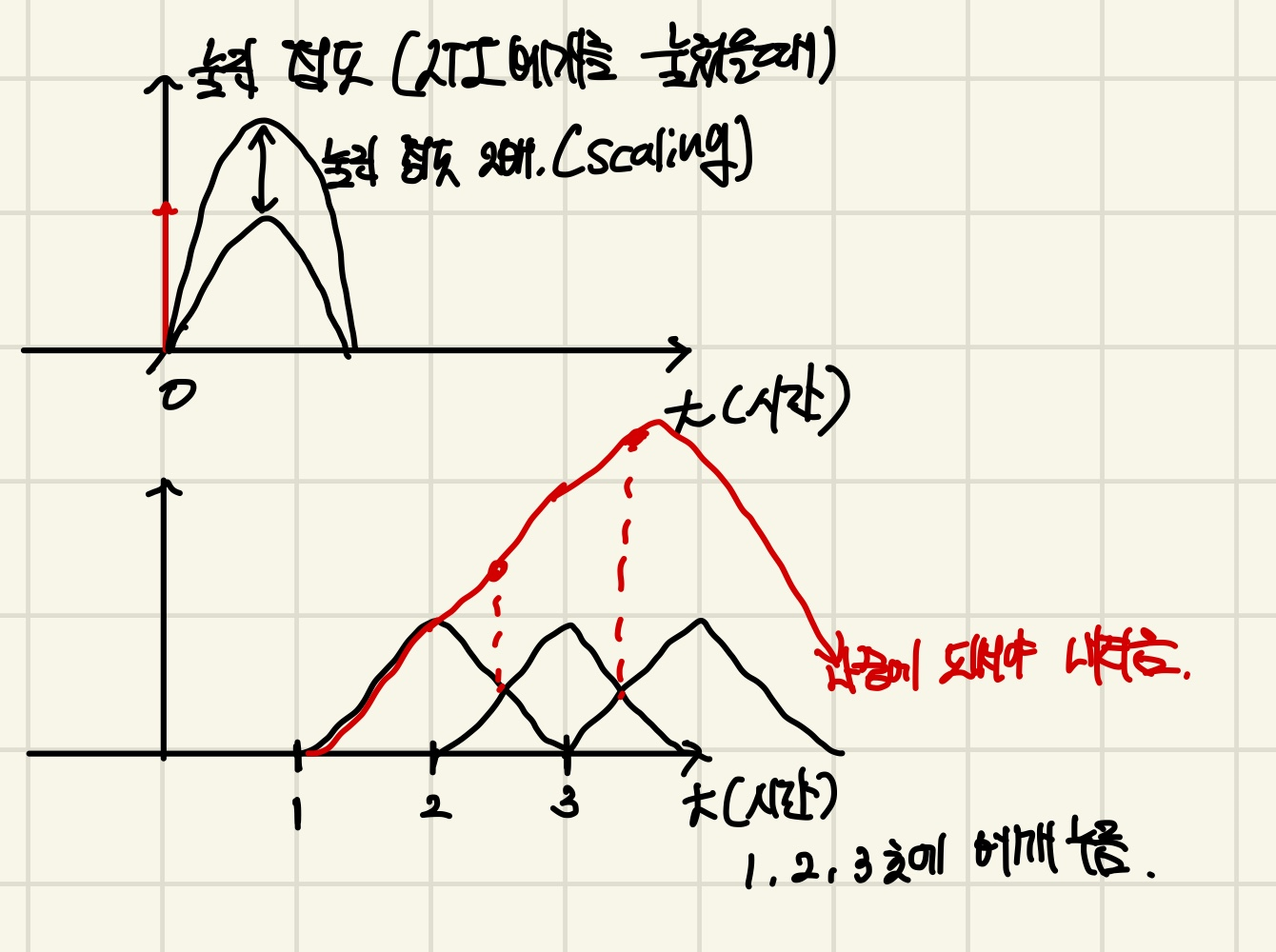
Linear는 Scaling과 Additivity를 만족시키면 Linear가 만족되는데,

어떠한 input signal $x(t)$와 output signal $y(t)$가 있다고 하자.
이때 $x(t)$에다가 상수 6을 곱하면 $6x(t)$가 되는데 이를 어떠한 system에 넣어도 output signal은 상수를 그대로 유지한 $6y(t)$가 되게 된다.

이를 Scaling을 만족한다고 한다.

$x_3(t) = x_1(t)+x_2(t)$의 input signal을 어떠한 system에 넣게 되면, $y_3(t)=y_1(t) + y_2(t)$을 만족시키게 되면

이를 Additivity를 만족했다고 한다.

따라서, 위의 Scaling과 Additivity 2가지의 성질을 포함해서 부르는 단어를 Superposition이라고 부르며 예시는 아래와 같다.

$ax_1(t) + bx_2(t) -> System -> ay_1(t) + by_2(t)$는 Superpostion을 만족하는 input signal이 된다.

Time Invariant

Time Invariant는 어떠한 signal이 시간의 변화가 주여져도 signal의 특성은 유지된다는 것이다.

이를 수식적으로 표현하면 $x_1(t-t_0) -> System -> y_1(t-t_0)$이라고 볼 수 있다.

그렇다면, 왜 우리는 이러한 LTI System을 배우는 것일까?
이는, 예측 가능한 system이기 때문이며 임의의 input에 대해서도 예측이 가능하기 때문이다.

예를 들어, 자판기에 1000원짜리 1개 생수를 사려고 했는데 1개의 생수가 나와야지, 3개의 생수가 나오면 안되며 시간의 변화가 주어져도 1000원짜리 지폐를 1개넣으면 생수 1개가 나와야하는 것이 당연하다.
따라서, 공학적으로도 이러한 예측 가능한 system을 통해서 signal을 분석할 수 있게 되는 것이다.

---

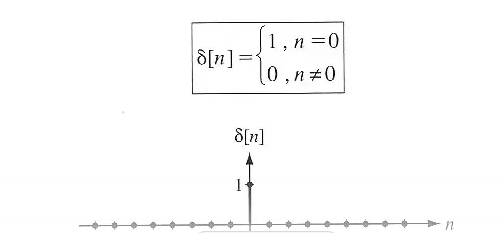
Impulse Function

$y(t) = f(x(t), h(t))$에서 h(t)를 Impulse Response라고 하는데, impulse function을 system에 넣었을 때 output을 이야기한다.

어쨋든, output signal $y(t)$는 input singal $x(t)$로도 표현할 수 있지만, $h(t)$로도 표현이 가능하다는 것을 알고만 있자.(신호를 구성하는 기본적인 단위로 작용한다)

이러한 Impulse Function은 Discrete과 Continuous로 성질이 나뉘는데, 아래를 참고하자.

Impulse Response

System을 정의한 것과 같이, Impulse function도 아래와 같이 표현할 수 있다.

$x(t)=δ(t) -> System -> y(t)=h(t)$, 위에서도 말했지만, h(t)는 impulse function을 system으로 가공시킨 output signal이며, Impulse Response라고 불리운다.

따라서, $y(t) = f(x(t), h(t))$에서 $h(t)$만 알고 있다면 $x(t)$에 대한 output도 계산이 가능하다.

"Sinal can be expressed by sum of impulses"로 impulse의 합으로 signal을 표현할 수 있는 정의가 있다.

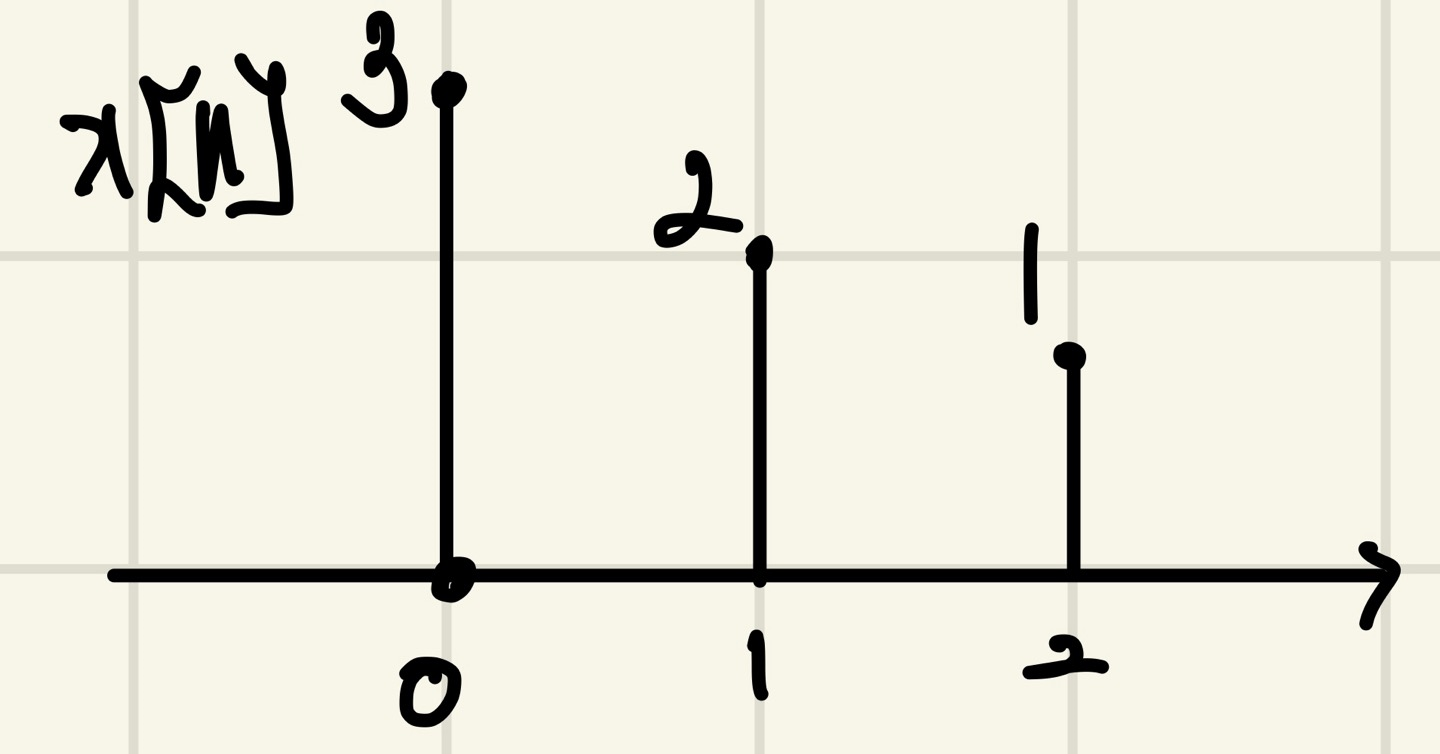
위와 같은 $X[n]$의 discrete signal이 있을 때, 우리는 이러한 signal을 impulse function으로 표현할 수 있다.

$X[n] = 3δ[n]+2δ[n-1]+δ[n-2]$이 된다.
이를 어떠한 초월함수를 근사화할 수 있는 다항식으로 표현할 수 있는 것을 테일러 급수라고 말한 적이 있는데, signal에서도 똑같이 표현된다는 것을 알고 있으면 이해하기가 수월하다.

따라서, 신호를 이렇게 표현할 수 있는 이유는 impulse function의 성질을 통해 알 수 있다.

그래서, $X[n]$을 System에 넣게 되면, $y[n]=3h[n]+2h[n-1]+h[n-2]$로 output signal로 표현된다.

Convolution

$Input Signal=x[-2]δ[n+2]+x[-1]δ[n+1]+x[0]δ[n]+x[1]δ[n-1]$
$Output Signal=x[-2]h[n+2]+x[-1]h[n+1]+x[0]h[n]+x[1]h[n-1]$

위의 output signal을 수식적으로 나타내면, $\displaystyle\sum_{k=∞}^{∞}{x[k]h[n-k]} =x[n]*h[n]$으로 표현되며, $x[k]$가 Scaling, h[n-k]가 time invariant의 성질을 가지고 있다.

따라서, x[n]과 h[n]을 convolution으로 나타낼 수 있다면 LTI System이다.

Convolution이란, 누적된 반응(impulse)을 계산하는 것이다.(아래 예시) 1개의 신호를 convolution으로 표현하며, 이러한 impulse response를 합쳐져 최종 output signal을 형성하는 것입니다.