Abstract

CNN operation을 통해서 sptial, channel-wise으로 fusing하면서 informative한 feature들의 정보를 얻을 수 있다고 한다. 이는 많은 visual task에 대해서 사용되는 operation이며 현재까지도 사용되고 있다.

또한, CNN을 통해서 feature들의 hierarchy를 구분 지을 수 있다. 처음에 있는 layer들은 img의 전반적인 feature들을 탐지하는 반면, 마지막에 있는 layer는 특정한 object에 대해서 더 specific한 정보들을 얻게 된다.

이렇게 filter들을 통한 output filter들은 img에 다양한 object들을 탐지하지만, mutually-exclusive하다는 단점이 있다.
따라서, SENet은 non-mutually exclusive하게 만들어준다고 한다. 이는 SEblock을 이용한다.

SEblock은 어느 특정한 dataset에 국한되지 않고 다양한 dataset에도 adaptive하다고 하니, generlize하다.

요약하자면, input img(data)에 따른 channel간의 response를 동적으로 recalibrate한다는 것이다.

---

Introduction

Section 1

Abstract에서 말한, CNN의 장점에 대해서 또 이야기하고 있다.(넘어가겠다.)

Computer vision는 image에서 powerful한 representation을 얻는 것이 목표인데, 이는 performance의 향상을 이끌어낸다.
따라서, 이는 architecture의 design이 search의 핵심이라고 생각하면 되겠다.

여기서 SEblock을 말하려고 build-up을 하고 있는데, 최근의 연구는 feature(channel)간에 상호관련성을 capture하는 mechanism연구가 활발히 진행되어지고 있다고 한다. 이를 inception architecture를 예시로 들면서 설명한다. (spatial attention을 사용한 inception을 말함)

Section 2

이 논문에서는, network의 다른 관점인 channel간의 relationship을 조사했다고 한다. 이는 새로운 architectual의 unit으로 "Squeeze-and-Excitation (SE) block" 이라고 한다.

이는 Abstract에서 말했지만, SEblock을 통해서 mutually exclusive한 것을 non-mutually exclusive하게 하였다고 하고, feature(channel)을 recalbrate하여서 informative feature들을 이용할 수 있게 되었다고 한다.(중요하지않은 feature들은 suppress하면서!!)

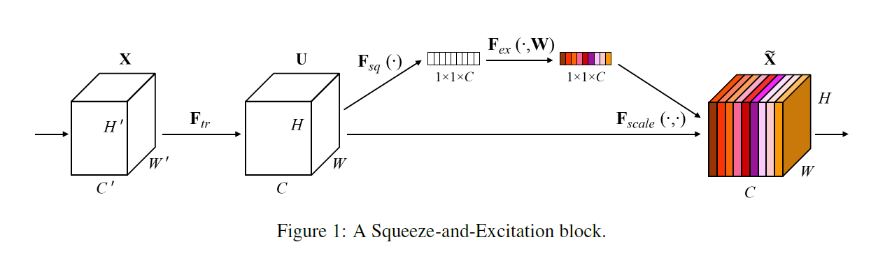
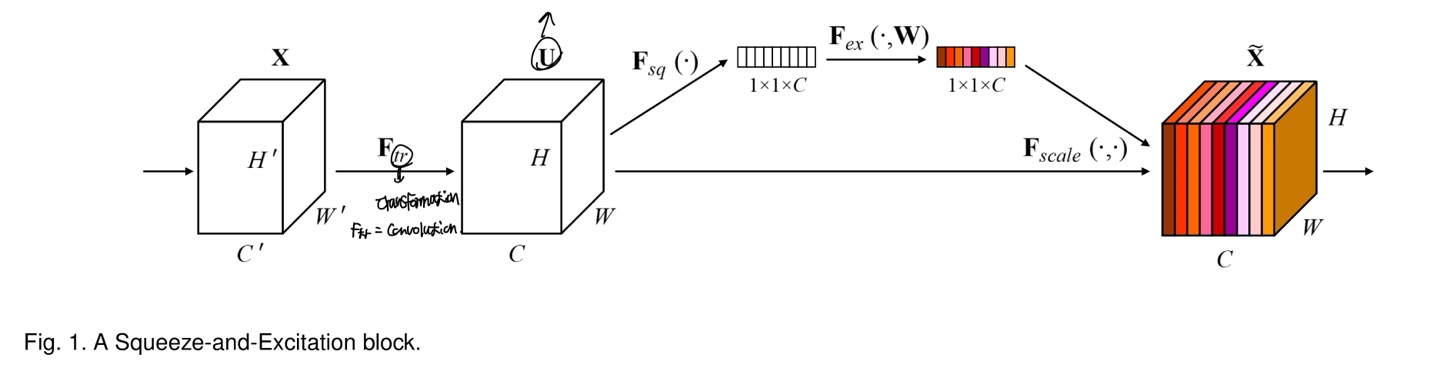
이제 SENet의 architecture(fig 1)을 보면서 설명한다.

input data인 X가 U로 mapping되어지는데, 이때 X가 U로 갈때 $f_{tr}$의 transformation을 이용한다고 한다. 이는 그냥 CNN을 적용한 것이다. CNN을 적용하였기 때문에 당연히 X와 U의 각 dimension의 value가 다를 것이다.

이때 SEblock에 들어가는 것은 U이며, U는 squeeze operation에 들어간다고 한다. 간략히 squeeze operation에 대해 설명하자면, U의 HxW를 1개의 feature로 줄이게 되는 것이다.(Global Average Pooling)

1개의 feature로 줄였으니 이는 vector로 표현이 가능하며, 이는 weight들의 값으로 되어있다. 즉, U가 1개의 vector로 표현되며, 이를 self-gating mechanism을 사용하여서 각 channel의 가중치를 부여한 것인데, 부여한 값들을 다시 U에다가 곱해지는 것이다.(뒤에 더 자세하게 설명할거임)

그니까 한마디로, excitation은 embedding한 vector를 input으로 받아서 U의 channel별로 weight를 부여한 것이다.

self-gating이란, 각 Input data에 맞게 weight를 동적으로 조절하는 것을 말한다.

Section 3

SEblock을 network에 적용하는 것이 가능하다고 나와있는데, 다양한 architecture에서도 적용이 가능하다고 보여진다.

좀 더 advance하게 이야기하고 있는데, network에서의 block의 역할 수행은 각자 다 다르다고 한다. 이는 layer마다 역할 수행이 다르다고 하는 것으로, 초반의 layer들은 class-agnostic한 정보들을 추출한다고 한다. 즉, class와 관련이 없는 response를 추출하게 되며, 이는 low-level의 feature들을 추출하는 것이다.

layer가 중첩될수록, feature들은 더욱 더 추상화 되어지며, 마지막 layer는 class-specific한 정보를 추출하게 되며, 이는 추상화 되어진 high-level의 feature들을 추출했다고 볼 수 있다.

이렇게 SEblock이 block(layer)마다 축점됨으로써 channel(feature)가 recalibrate될 수 있다고 한다.(weight를 동적으로 할당하기 때문에!!)

Section 4

새로운 CNN architecture를 만드는 것은 매우 어려운 작업이라고 한다. 하지만 SE block은 매우 간단하며 최신 architecture에 대체하기에 매우 쉽다고 한다.

또한, SE block은 적은 개수의 weight만을 architecture에 넣어주기 때문에 model의 complexity와 computation이 조금 증가한다고는 한다.

성능은 확실히 좋아지는 것을 지표상으로 볼 수 있다.

---

Related Work

Deeper Architectures

여기는 SENet이 나오기전에 method에 대해서 설명하고 있는데, 차례대로 살펴보자면 다음과 같다.

먼저, VGG와 Inception에서는 network의 depth가 증가할수록 성능이 좋아지며, BatchNormalization을 통해 학습이 원활하게 될 수 있다는 장점이 있다.
또한, ResNet의 identity-mapping인 shortcut을 통해 network의 depth가 더 증가할 수 있다. 이는 backpropagation과 관련이 있으며 자세한 것은 ResNet논문 참조를 바란다.
Self-gating에 대해서도 설명하고 있는 것을 볼 수 있다.

첫 3줄에서 network에 포함된 operation component function의 형태를 개선하고자 했는데, 이는 다양한 convolution의 기법을 이야기하는 것 같다.

Grouped Convolution에 대해서 설명하고 있는데 이는 자세히 다뤄보겠다.

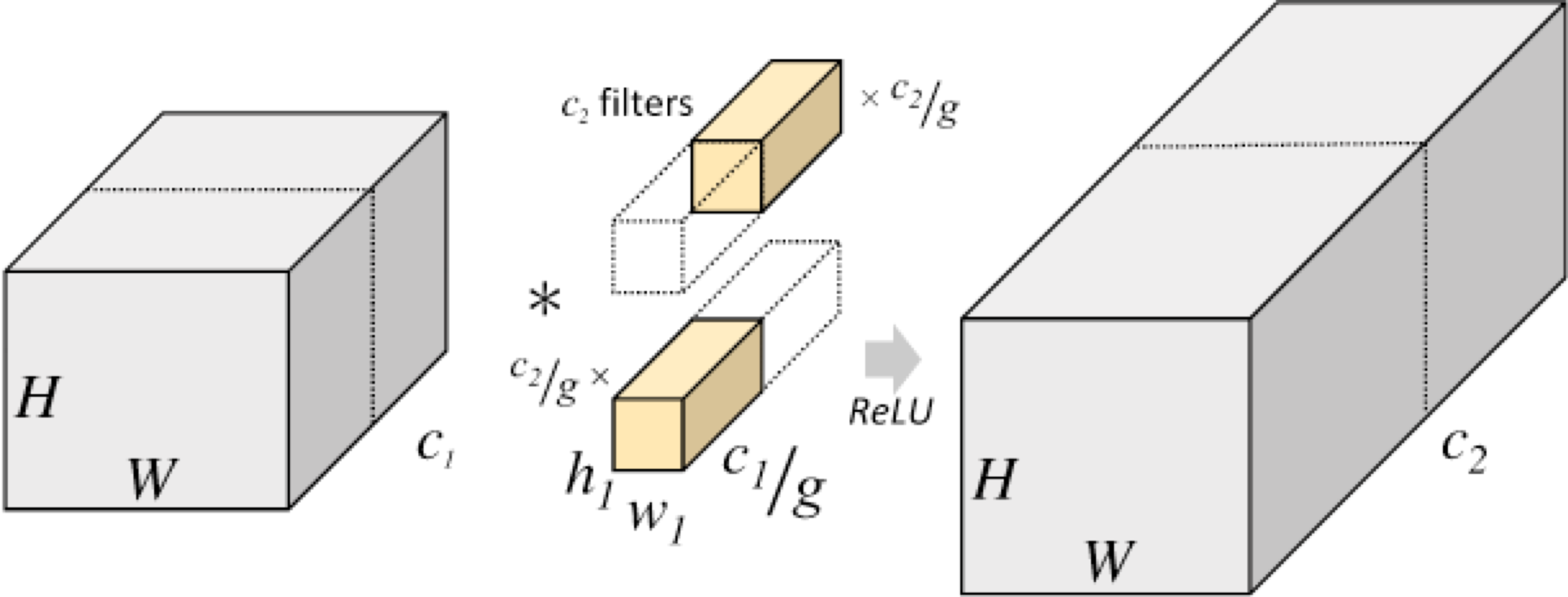
group convolution은 input의 channel들을 여러 개의 group으로 나누어 독립적으로 convolution을 수행하는 것인데, 이는 기존의 convolution보다 낮은 parameter수로 이에 따른 연산량도 적어지게 된다.

또한, 병렬처리에 유리하다는데 이는 내가 병렬처리를 자세히 공부하지 않아 일단 받아들였으며 각 group에 높은 상호관계를 가지는 channel이 학습될 수 있는 것은 확실하다.

parameter의 수를 알아보자
먼저 input channel들을 g(group 개수)개의 group으로 나누어 연산을 진행할 것인데, 전체의 channel의 수가 c라면, 각 group당 $\frac{c}{g}$개의 channel이 있게 된다. 그러면 이 값이 input이 되겠다.

output channel이 m이라면, output channel도 group에서 $\frac{m}{g)}$이 된다. 그러면 1개의 group당 $k^2$x$\frac{c}{g}$x$\frac{m}{g}$이 되는데 g개의 group이 있으니, $k^2$x$\frac{c}{g}$x$m$이 되겠다.

• $k^2$은 kernel의 크기

• $\frac{c}{g}$ : filter의 depth

• $\frac{m}{g}$ : filter의 개수(output filter의 개수)

다음 문장은 BottleNeck구조인 1x1 convolution에 대해 설명하고 있으며, 또 그 다음은 SEblock에 대해서 간략하게 설명하고 있다.

(Algorithmic Architecture Search와 Attention and gating mechanisms은 SEblock에서의 설명은 거의 없으니 뒤에서 더 자세히 설명하겠다.)

---

Squeeze-and-Excitation Blocks

Input data인 X를 $F_{tr}$의 transformation으로 U로 만든다고 한다.
이때 $F_{tr}$은 convolution연산이며, X의 dimension이 H'xW'xC'였다면 $F_{tr}$의 convolution연산으로 X가 U로 HxWxC의 dimension으로 바뀌어진다.

여기서 나타내는 V는 filter의 집합을 나타내며, V의 filter개수가 C이기 때문에 U의 channel의 dimension이 C인 것을 알 수 있다.

그래서 수식을 보게 되면, V의 집합안에서 $v_c^s$ * $x^s$는 channel간의 mapping으로 convolution연산을 취하는 것이며 이를 전체의 channel로 적용한 후 더해주면 된다. 그냥 convolution연산임..
그래서 $u_c$는 input data에 1개의 filter에 convolution을 진행시켜주었으며 dimension이 HxW가 된다.

위의 수식에서 bias는 생략했다고 한다.

이 뒤에 나오는 문장이 조금 중요해보이는데, top-most layer는 신경망의 가장 마지막 위치에 있으며 output layer로써 결과를 생성한다고 하는 것이라고 한다. 이는 channel간의 관계가 더 명시적일 수 있다고 하며 channel간의 관계가 화경낳게 들어난다고 한다.

top-most layer를 제외하고 channel간의 관계는 본질적으로 임시적이고 지역적인 특성을 가지고 있다고 한다. 그니까 직접적으로 response를 표현하지 않고 간접적으로 표현한다고 한다. 이는 receptive field가 적다는 이야기이다.

Squeeze : Global Information Embedding

첫 문장에서 channel간의 dependency를 알아내기 위해서는 output features안의 각각의 channel의 signal을 고려해야한다고 나와있다. 여기서 signal 단어에 주목해야하는데, 공학에서의 signal은 vector형태로 표현된다는 것이 핵심이다. 이는 U의 channel을 channel-wise로 vectorization을 시킬 것이라는 시발점이 된다.

이를 Local receptive field로 딥러닝관점에서 다시 설명하고 있는데, local receptive field는 각 filter가 고려하는 input data의 region을 의미하는데 이는 주변의 contextual 정보를 이해하지 못한다는 단점이 존재한다고 한다. 왜냐하면, 해당 지역 내에서만 고려하기 때문이다.

이러한 문제를 해결하기 위해서, local receptive field를 vector로 변형시키는 global average pooling을 사용한다고 한다. 위의 수식이 GAP에 대한 수식이다.

먼저 $u_c$의 kernel의 pixel값들을 다 더하고 그것은 resolution의 값으로 나누어주면 된다. 그러면 output값인 $z_c$가 나오게되며 이는 1x1의 dimension을 얻게 된다.

GAP은 굉장히 간단하고 명료하며 GAP말고는 정교한 method가 없었다고 한다.

Excitation: Adaptive Recalibration

channel간의 중요도를 알아보게 되면 다음과 같은 2가지의 효과를 얻을 수 있다고 한다.

• flexible

• non-mutually exclusive relationship

위 2가지 효과가 어떻게 일어나는지 수식을 통해 알아보자.

빨간색으로 highlight한 부분에서 맨 오른쪽의 수식으로 설명하겠다.
z는 GAP을 적용한 output으로 dimension이 Cx1이 되고 이를 $W_1$(weight)와 곱해지게 된다.
$W_1$의 dimension은 $\frac{C}{R}$x$C$이고 이를 z와 곱해주게 된다.

즉 $W_1$ x $z$의 dimension은 $\frac{C}{R}$x$1$이 된다. 이에 대한 결과값을 ReLU에 넣어주게 되고 이를 다시 $W_2$로 곱해지게 되며, $W_2$의 dimension은 Cx$\frac{C}{R}$이므로 dimension은 Cx1이 되겠다.

이를 다시 sigmoid function으로 넣어주며 non-linearity와 normalization의 효과를 얻을 수 있다.

이러한 S의 값들을 X에서 $F_{tr}$의 transformation으로 U에다가 S를 channel로 mapping되어지게끔 곱해주면 된다.
그러면 최종 output은 중요도가 반영된 $X^{hat}$이 된 것을 볼 수 있다.

이렇게 channel들을 동적으로 중요도를 할당해줌으로써 매우 flexible하며 channel간의 중요도를 알 수 있으며 non-mutually exclusive하다는 장점이 생기게 된다.

---

GitHub에 VGG16에 SEblock을 추가해서 구현했습니다.

읽어주셔서 감사합니다.