RNN

Multivariate Time Series Data

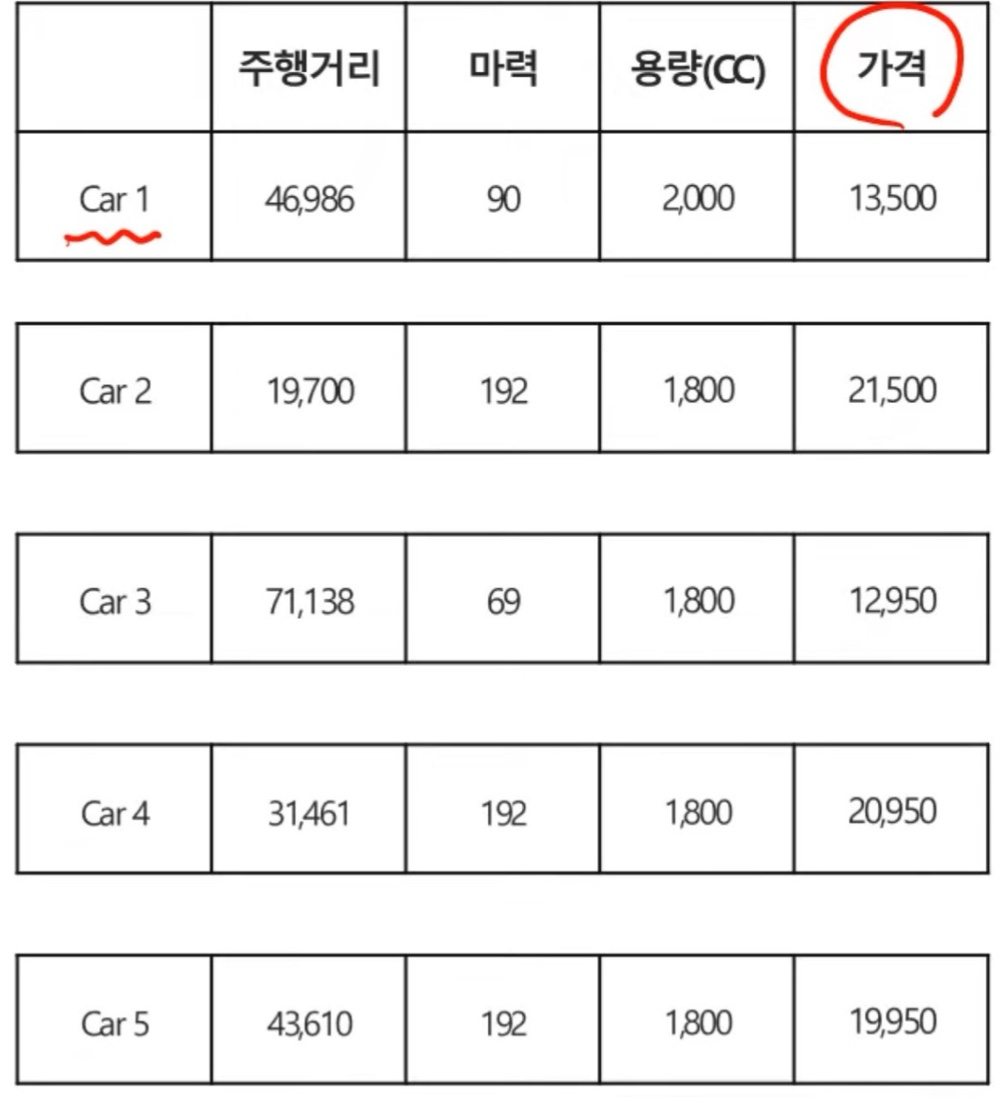
위의 Car의 가격을 예측하기 위해서 주행거리, 마력, 용량(cc)의 정보들을 통해서 Car5의 가격을 예측한다고 한다면 이 Car1~Car4의 데이터의 순서가 중요할까?

당연히 순서가 중요하지 않고 모델이 이 data들을 잘 학습만 해준다면 주어진 데이터로 Car5의 가격을 예측할 수는 있을 것이다.

우리는 이렇게 데이터의 순서가 중요하지 않고 서로 독립인 데이터를 "독립 데이터"라고 부른다고 한다.

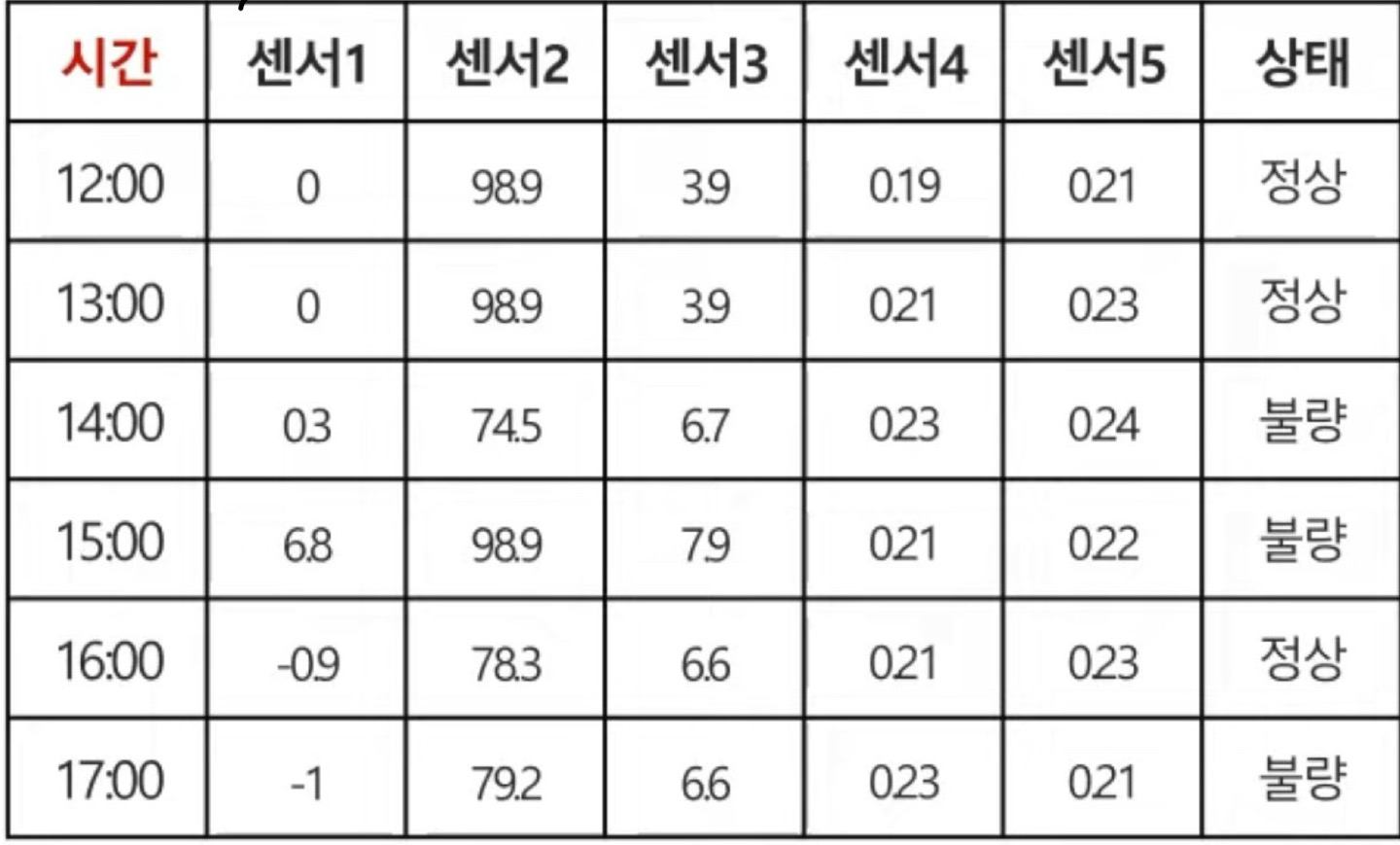
하지만 위의 훈련 데이터의 변수들중에서 "시간" 이라는 변수가 생겼다. 그렇다면 주어진 데이터로 새로운 Car의 상태를 예측하기 위해서는 시간에 따른 데이터의 순서도 매우 중요하게 작용할 것이라는 것을 알게 된다. 왜냐하면 시간은 순서가 있는 데이터중 1개이기 때문이다.

우리는 이렇나 데이터를 "Multivariate Time Series Data(다변량 시계열 데이터)"라고 부르기로 하였다.
이러한 데이터는 Sequence Data의 부분집합이라고 생각해주면 되고, Sequence Data는 순서에 따라 얻어진 Data이다.

즉, 정리하자면 Time Series Data는 시간의 흐름에 따라 관측되어 시간의 영향을 받게되는 데이터이며, 현재의 상태가 과거의 상태에 영향을 받게 되는 data이다.

---

RNN 필요성

우리는 이미 DNN에 대해서 배우기로 하였다고 가정하고 설명하겠다.
DNN은 이전 시점의 정보를 반영하지 않는 네트워크라는 것을 알 것이다. 즉, 현재 그 상태에 대한 변수들만으로 상태를 예측하게 되는 것인데, 우리는 이러한 DNN을 가지고 시계열 데이터를 잘 예측할 수 없다는 것이 DNN의 한계점으로 나타나게 되었다.

그러면 단순하게 DNN의 hidden layer의 node들에 그냥 이전 정보들에 대한 데이터를 참고만 되지 않는가? 라는 발상으로 RNN이 만들어졌다.

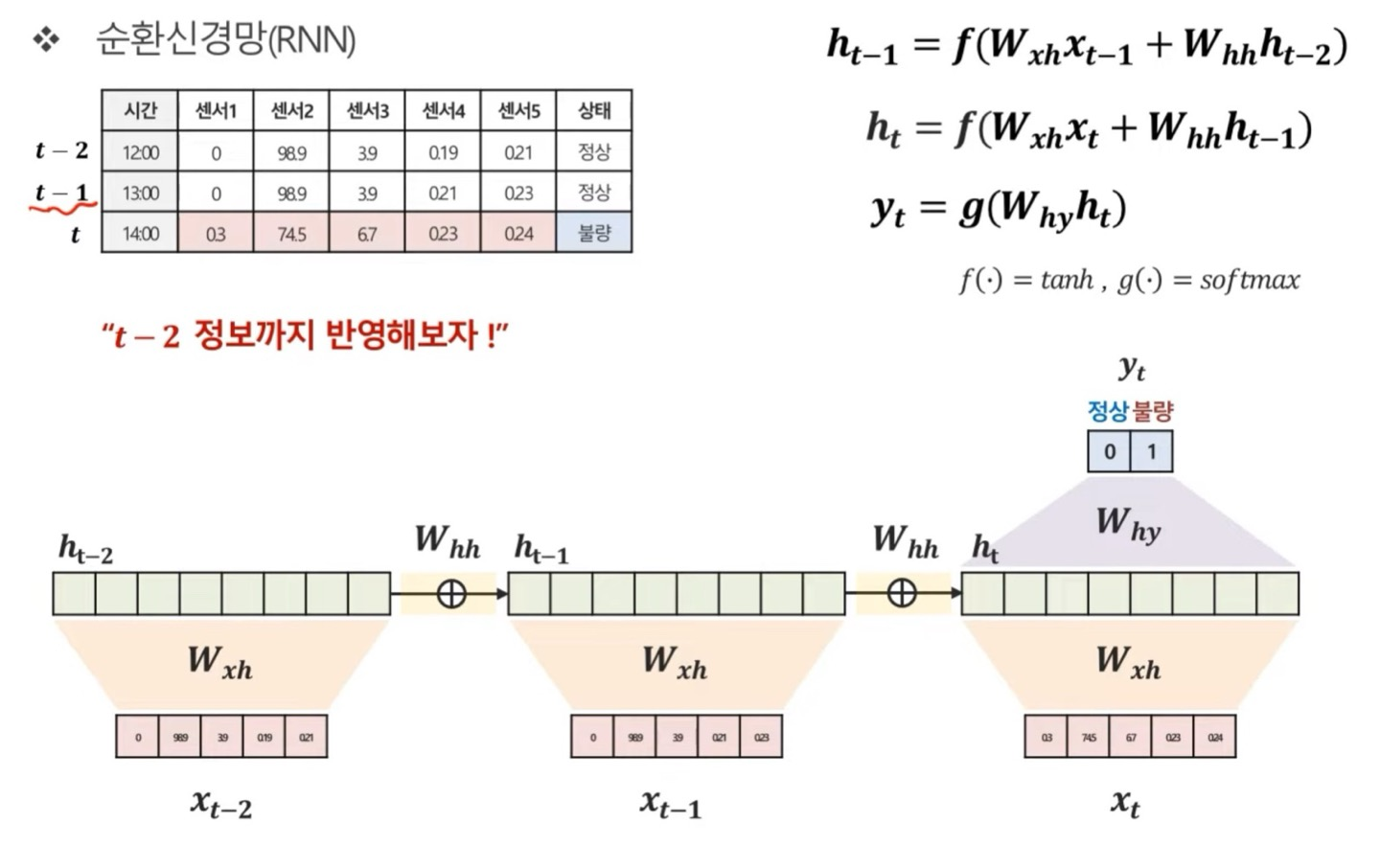
그러면 t(현재 시점), t-1(이전 시점), t-2(t-1의 이전 시점)의 대한 시계열 데이터가 있다고 해보자
이때 우리가 구하고 싶은것은 현재 시점 t에 대한 "상태(output)"값만을 구한다고 하기로 하자

오른쪽 상단의 수식을 한번 봐보면 $h_{t-1}$은 $h_{t-2}$의 대한 정보를 가진 것으로 생각할 수 있다.$(W_{hh}$는 이따 설명하겠다.) 그러면 이전 hidden vector(state)는 $h_{t-2}$에 대한 정보를 가지고 있게 되고 수식을 계속 따라가다보면 $h_t$는 $h_{t-1}$에 대한 정보, 즉 $h_{t-2}, h_{t-1}$의 정보들을 가지고 있게 된다
그런 다음 $y_t$를 통한 weighted sum을 통해서 output값을 도출해내게 된다. (f()랑, g()는 Activation Function이다)

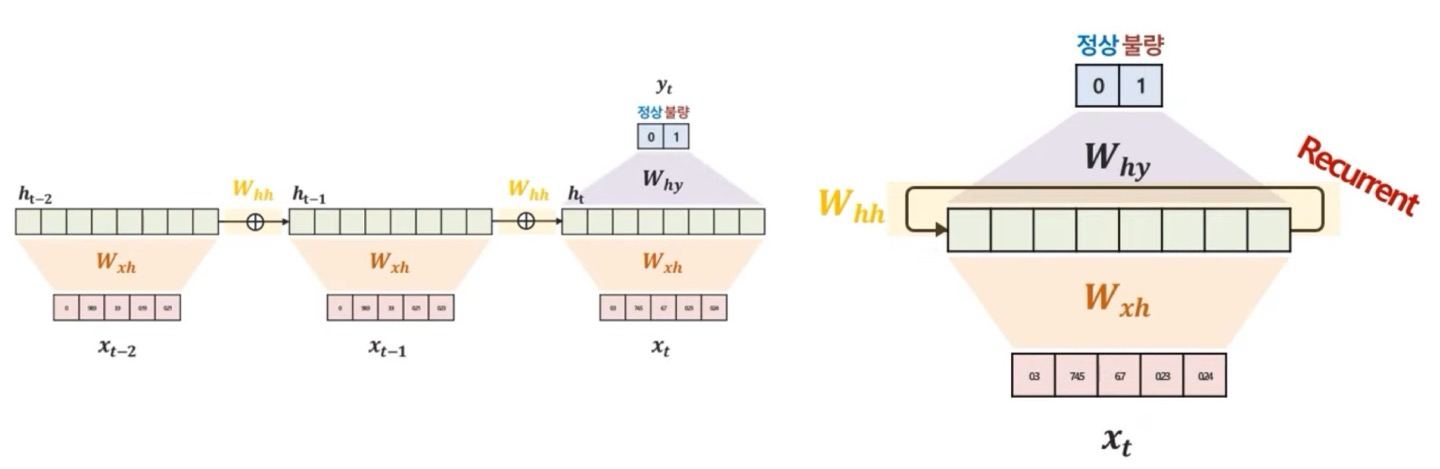
글로 설명하는 것보다 그림으로 보면 더 빨리 이해가 될 것 같다.

그런데, 1가지 의문이 든다. 기존의 MLP와 CNN과는 달리 RNN은 생각보다 weight들이 복잡하게 얽혀있는 것 같은데 어떻게 구분을 지어야할지 필자도 궁금했다.

수식을 보면 알겠지만, weight의 종류는 다음과 같다.
Weight는 같은 값을 공유하는 것이 핵심이다.

• t 시점 data 반영 : $W_{xh}$ (데이터에서 hidden vector의 weight)

• t 시점 이전 정보 반영 : $W_{hh}$ (hidden vector에서의 parameter sharing weight)

• t 시점의 y를 예측 : $W_{hy}$ (hidden vector에서 output값까지의 weight)

이 3가지의 종류의 weight들이 학습 대상이며 매 시점마다 공유하는 구조로 parameter sharing이라고도 불리우게 된다. 왜냐하면 hidden vector로 가게 되면서 weighted sum이 되기 때문이다.

---

RNN 구조 다양성

RNN의 종류는 input의 길이, output의 길이에 따라 구별이 된다고 보면 된다.

Many to one

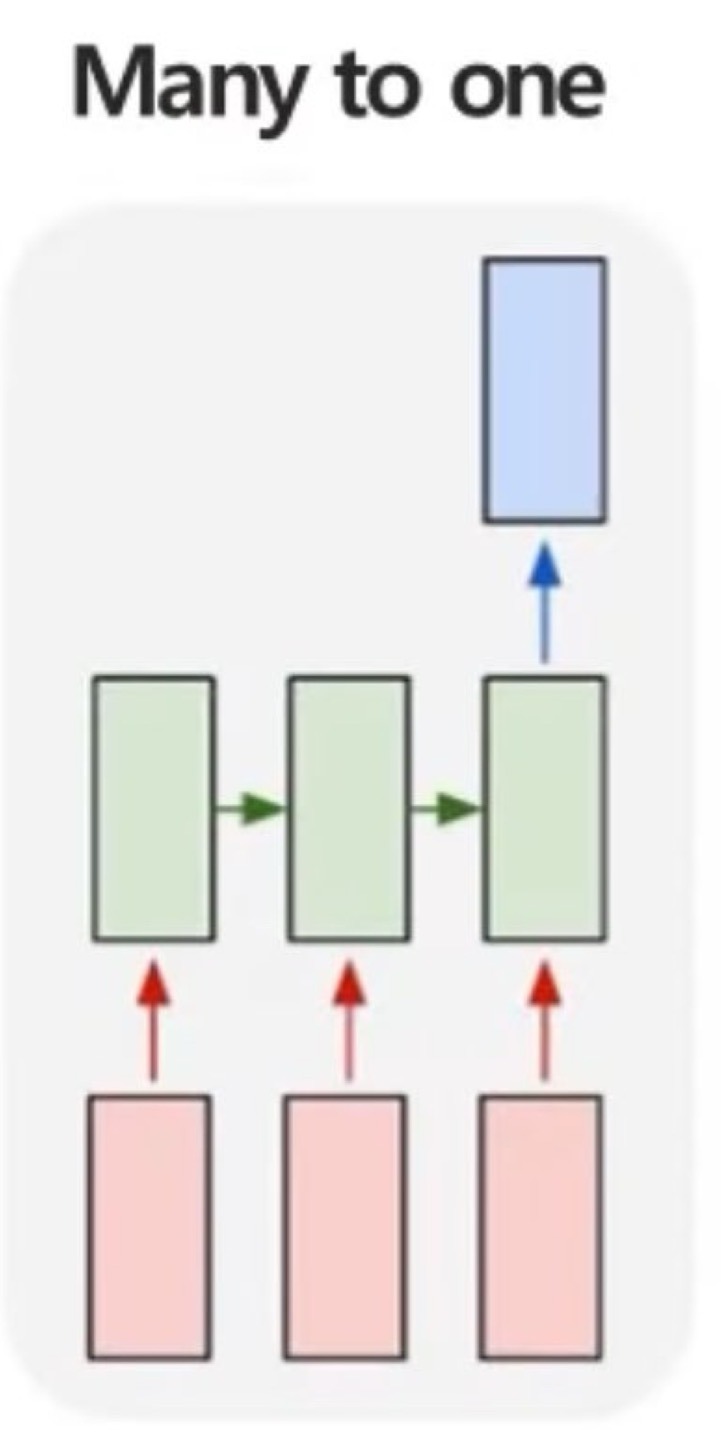
우리가 앞에서 다룬 내용이 Many to one의 구조이다. 여러 시점(t, t-1, t-2 ,,)에서 하나의 output을 만들어내는 문제인 구조라고 생각해주면 된다.

예시를 굳이 들자면, 여러 시점에 다변량 데이터가 주어졌을때 특정 시점의 제품 상태를 예측하는 것이 있다고 한다.

One to Many

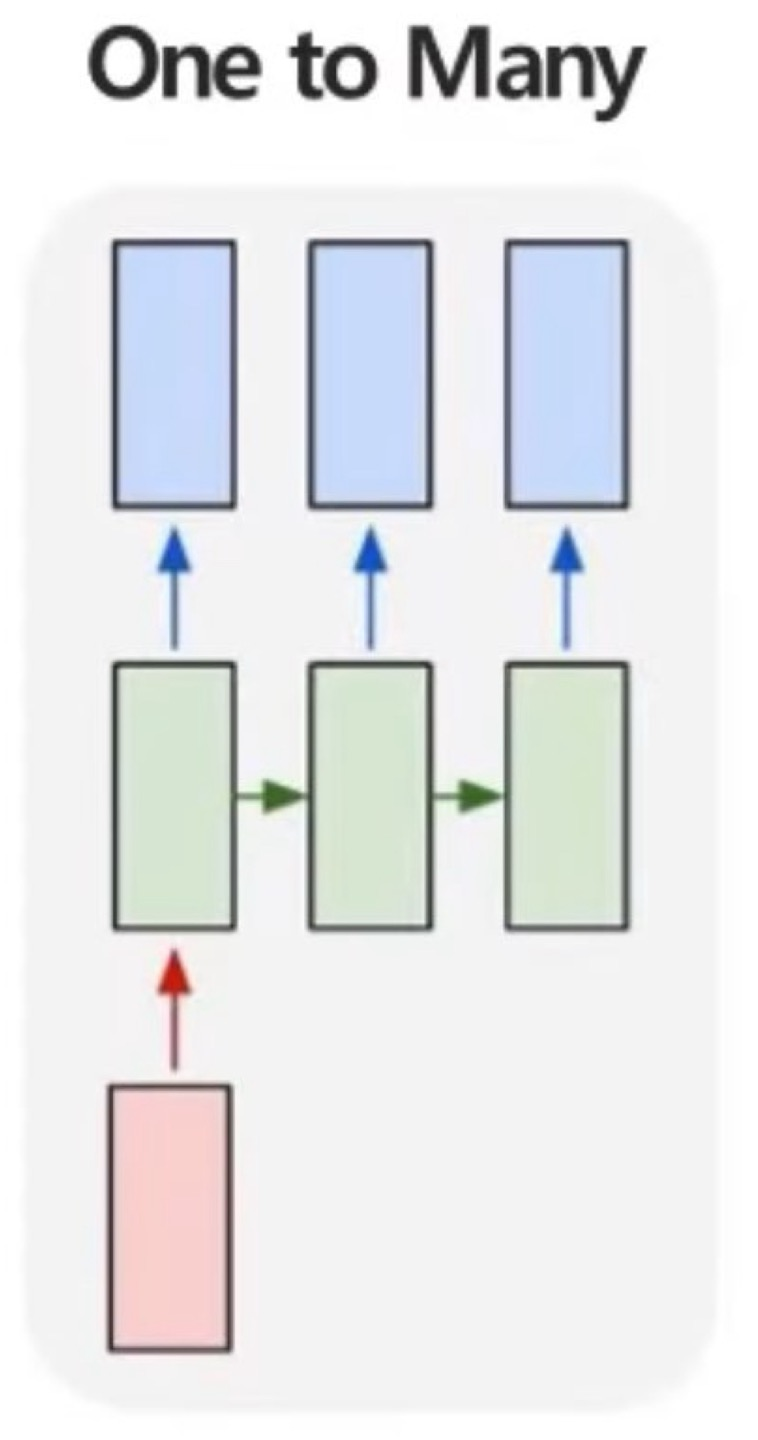
One to Many는 한개의 input data가 들어갔을때 sequential한 output을 예측하는 문제이다.
예를 들면, 1개의 img data가 들어갔는데, img에 대한 정보를 글로 생성하는 "Image Captioning"이 있다고 한다.

Many to many

Many to many에서 좀 더 advance한 Many to one + one to many구조를 한번 봐보자

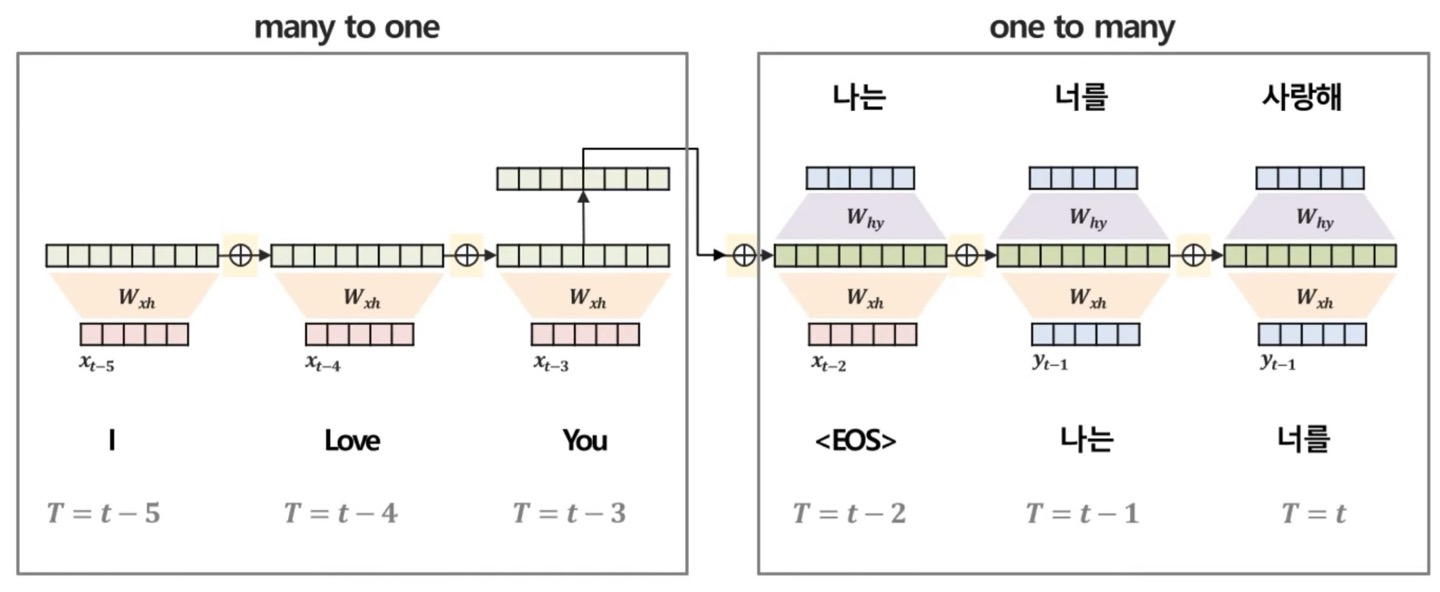
구조만 보면 쉬워보인다.그냥 Sequential한 input data를 넣고, Sequential한 output data를 출력하는 것이다.

이러한 구조는 Many to one이 이제 Encoder, one to Many가 Decoder라는 부분인데 대표적으로 Sequence to Sequence 모델이 있다.

추후에 다룰거지만, 간략하게 이야기하자면 Encoder는 입력된 sequential data를 요약하여서 요약 벡터를 생성하고, Decoder는 요약 벡터를 기반으로 sequential한 output data를 predict하는 역할을 한다.

예를 들자면, 번역하는 문제가 대표적인 예시가 될 것 같다.

---

RNN 학습

RNN의 학습은 우리가 이때까지 해왔던 weight들을 update하는 pipeline이게 되는데, 우리가 이전까지 배웠던 것과 다르지 않다.

1. Forward-pass를 통해서 loss 계산
2. Backpropagation
3. weight update

만약 gradient descent를 까먹었다면 다시와서 보는 것을 추천한다.

Forward-pass를 통한 Loss 계산

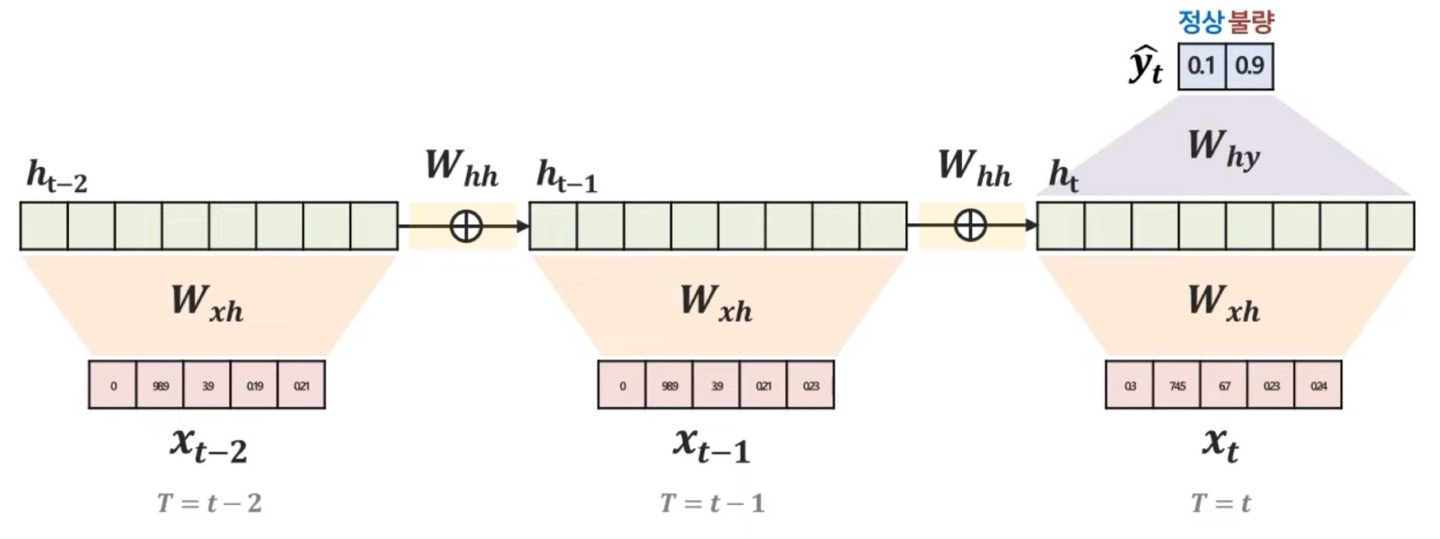
Forward-pass는 loss를 계산, predict값을 예측하는 것으로 봐도 된다.

$h_t$는 이제 앞에서 사용한 hidden vector가 아닌 hidden state로 쓰겠다. hidden state는 이전의 hidden state까지 정보를 포함한 것으로 생각할 수 있다.
수식으로 나타내면 $h_t = tanh(W_{xh}X_t + W_{hh}h_{t-1})$로 앞에서의 내용이 이해가 갔으면 여기도 쉽게 이해가 될 것이다.

이 $h_t$는 weighted sum한 값으로 tanh를 썼으니 -1 ~ 1사이의 값으로 정규화 된 값을 가지게 된다.
$y_{hat_t} = softmax(W_{hy}h_t)$이니 분류 문제인가보다. 0 ~ 1사이의 정규화 된 값을 가지게 되고
$L_t$는 label과 predict의 차이, 즉 $y_t와 y_{hat_t}$의 차이가 된다.

hidden state의 계속 weighted sum되면서 최종 $y_t$에 대한 $h_t$를 구한 다음 output값을 도출하고 loss를 계산하면 된다.

하지만, 앞선 RNN의 구조에서 One to Many, many to many는 output의 개수가 많은데 어떻게 loss값을 어떻게 구해야하는지 필자는 배워본 적이 없다.

그냥 각각의 output(predict)값에 label값의 loss값을 구하여 평균을 구한다고 한다.

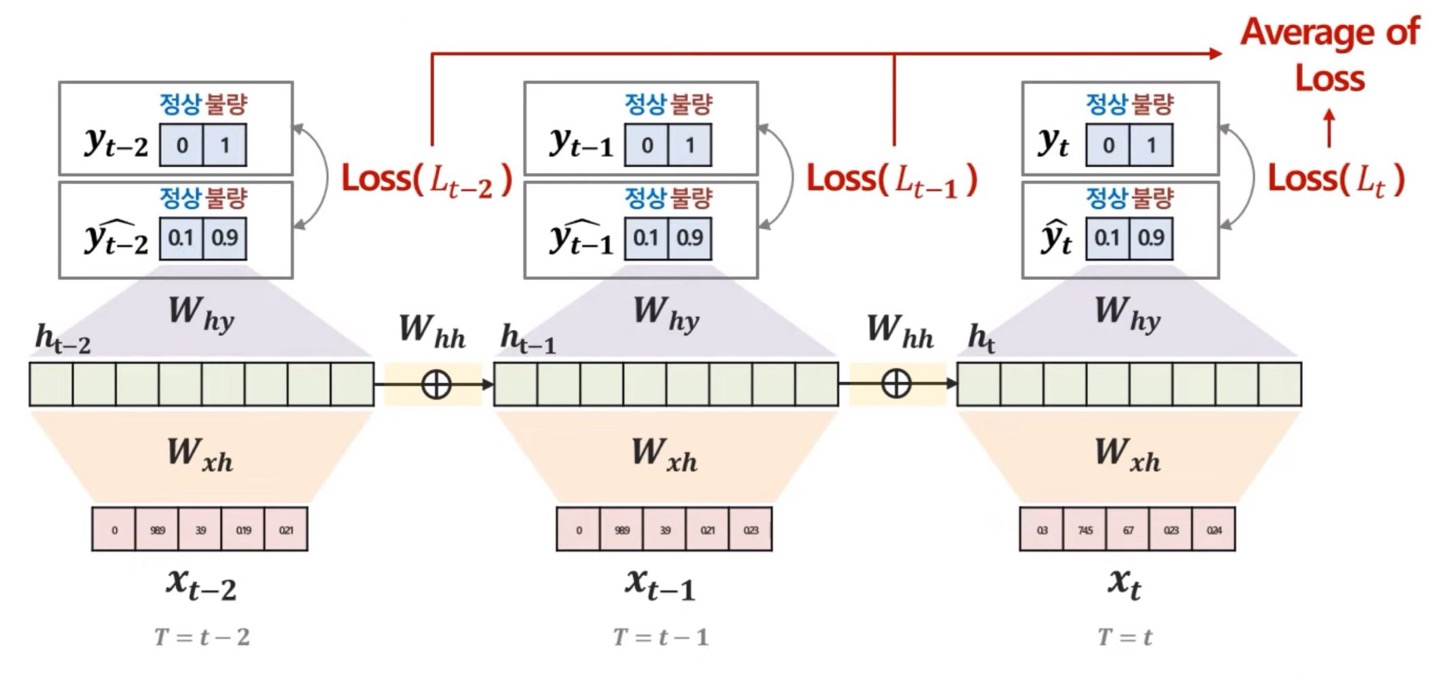
위의 그림을 보고 금방 이해가 될거라고 생각한다.

Backpropagation

RNN에서의 backpropagation은 BPTT(Backward Propagation Through Time)이라고 불리우는데, 그 이유를 찾아보니 시간에 따라 반복되는 RNN의 구조를 감안하여 역전파가 이루어진다고 해서 붙여진 이름이라고 한다.

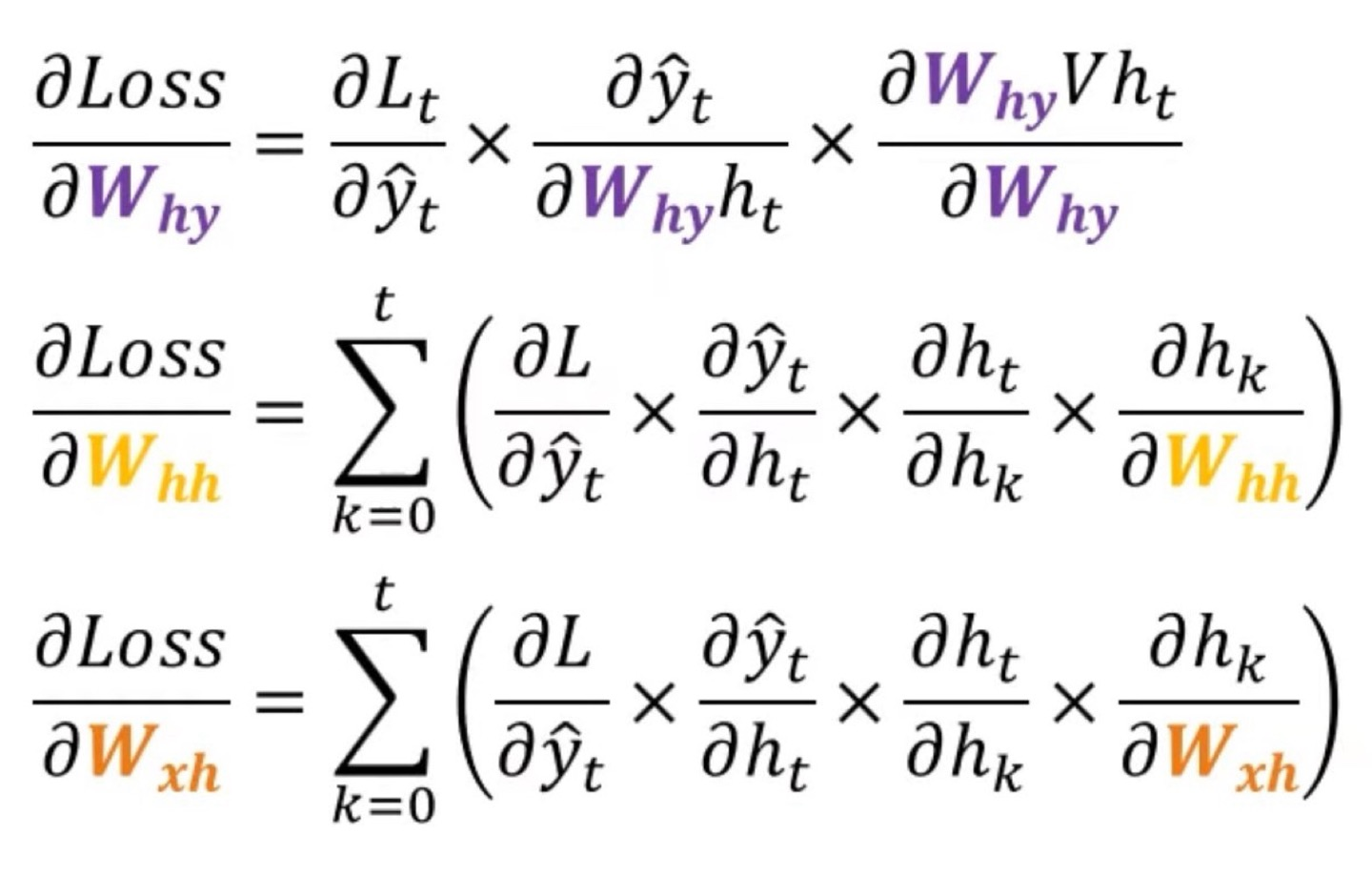
위의 img는 각 weight의 종류마다 gradient를 구한 공식이라고 보면 된다.

$W_{hy}$에 대한 gradient는 이해가 되었을거라고 생각한다 $y_{hat_t}$를 $W_{hy}h_t$에 대해 편미분하는 이유는 softmax함수가 $y_{hat_t}$으로 이루어져있기 때문이다. (혹시라도 궁금해할까봐..)

$W_{hh}와 W_{xh}$에 왜 ∑가 있는지 궁금할거 같다.
3개의 시점으로만 이루어진 RNN이라고 해보자(t, t-1, t-2의 시점만 있다고 가정)

$W_{hh}와 W_{xh}$는 각 시점마다의 gradient를 구하고, 다 더하는 구조이기 때문에 ∑가 있는 것으로 생각하면 된다.(시점마다 더하는 것으로 생각)

사실 MLP와 CNN의 backpropagation을 수학적 수식으로 이해했으면 이것만 보고 이해할 것이라고 생각한다.

Weight Update

Weight update부분은 gradient descent의 식을 통해서 weight를 update하는 것으로 gradient를 구하고 hyperparameter인 learning rate를 설정하여 새로운 weight를 구하면 된다.

이 부분은 크게 어렵지 않으니 넘어가겠다.

---

RNN의 한계점

RNN의 한계점을 결론부터 말하자면 long-term dependency problem(장기 의존성 문제)가 발생하는데, 이것을 정의하자면 input data의 sequence data의 길이가 길어질수록, 처음 부분(과거 정보)에 대한 학습에 어려움이 발생하게 되는데 이는 "Vanishing Gradient"의 문제가 핵심이다.

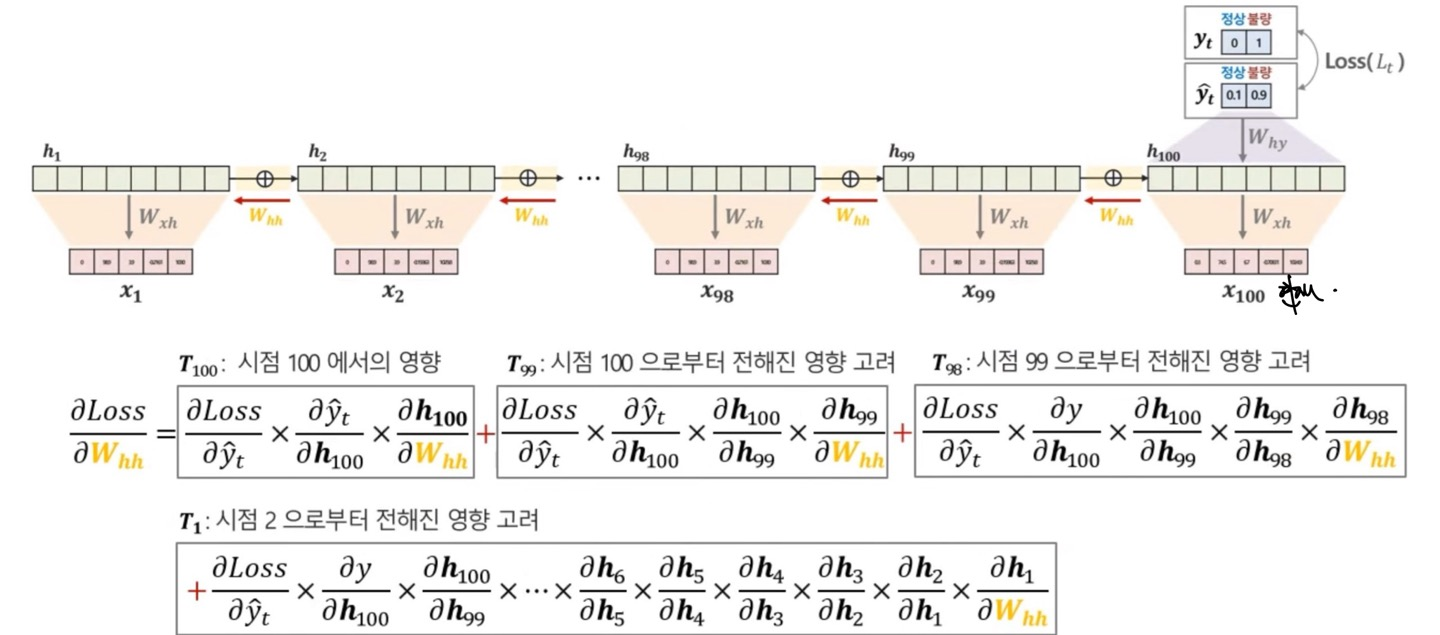
위의 식을 보게 되면 $W_{hh}$에 대한 gradient를 구하는 식이다.
gradient의 식을 보게 되면 처음 $T_{100}$에서의 영향과 $T_1$에서의 식을 보게 되면 확연히 $T_1$에서의 곱셈 연산이 더 많이 들어가는 것을 볼 수 있다.

물론 $T_{100}$과 $T_1$을 놓고 보면 $T_{100}$이 더 작을 수 있지만, $T_1$이 더 작은 확률이 당연히 더 높다.
왜냐하면 RNN의 구조에서 activation function으로 tanh함수를 쓰기 때문인데, tanh의 gradient의 range는 0~1사이의 값을 가지기 때문이다.

이제 다시 $T_1$의 식을 보게 되면 $\frac{h_t}{h_{t-1}}$에 대한 식이 많은데 이것은 tanh를 $h_{t-1}$에 대해서 미분하라는 것과 같다.
수학적 수식으로 나타내자면, $h_t = tanh(W_{xh}X_t + W_{hh}h_{t-1})$인데 $\frac{h_t}{h_{t-1}}$ = $tanh'(W_{xh}X_t + W_{hh}h_{t-1})W_{hh}$가 되게 된다.(다시 말하지만 0~1사이의 값을 가지게 된다.)

그렇기 때문에 굉장히 이전 시점에 대한 gradient는 0에 가까운 값을 가지게 됨으로써 parameter를 update할때 아주 작은 정보만을 가지고 있는 weight에 대해 update함으로써 초반 시점에 대한 정보는 매우 부족하게 된다.

이러한 문제점이 바로 long-term dependency problem이라고 한다.

---

LSTM

LSTM(Long Short Term Memory)는 RNN의 long-term-dependency의 problem을 완화한 RNN의 개선 모델이다.
당연히 RNN과의 architecture도 다른데, 기존의 RNN에서 Cell State와 3가지의 gate를 추가하여 위의 문제점을 해결했다고 한다.(까먹지 말아야할 것은 Vanishing Gradient문제가 제일 핵심!)

Architecture

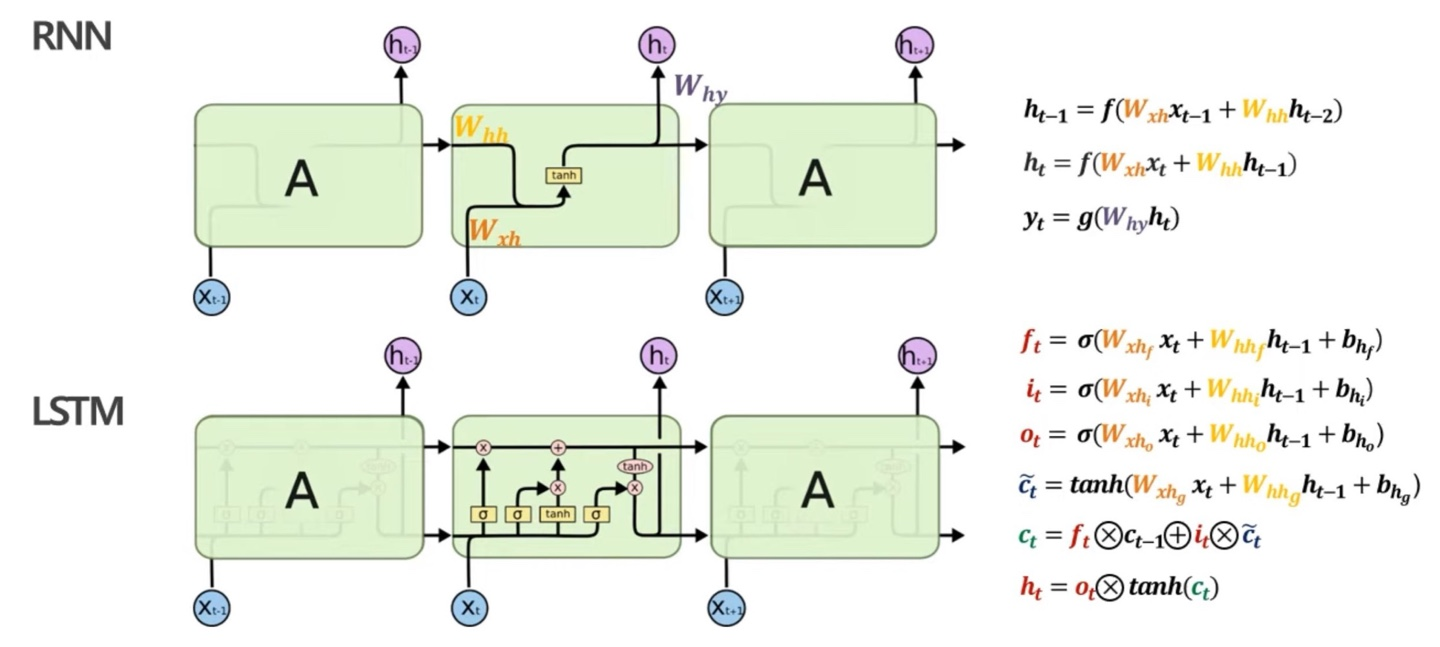
RNN과 LSTM의 모델을 비교해볼때 얼핏봐도 LSTM의 모델이 더욱 복잡하다는 것을 알 수 있다. 이는 3가지의 gate를 구하는 과정과 $C_{hat_t}$, $C_t$를 구하고 hidden state를 구하기 때문에 과정이 복잡하다.

pipeline에 대해 설명할건데, 이는 LSTM의 오른쪽 수식만 봐도 한눈에 이해될 수 있다.
$h_t$를 구하기 위해서는 $c_t$를, $c_t$를 구하기 위해서는 $c_{hat_t}$를,, 결국 차례로 $f_t$ ~ $h_t$까지 순서대로 구해야한다.

즉, t시점에서의 hidden state을 구하는 것이 관건이다. 왜냐하면 예측 값인 $y_{hat_t}$를 구할 수 있으니까

Abstract

Cell state의 역할은, 장기적으로 정보들을 유지할 수 있도록 조절하는 vector로 hidden vector를 구하는데 cell state를 이용한다고 하여 Vanishing Gradient 문제를 해결하게 된다.

3가지의 gate를 통해서 cell state와 hidden state를 update하게 되며, $c_t$를 구하기 이전에는 3가지의 gate를 구하고 $c_{hat_t}와 c_t$를 구해야한다.

먼저 $c_{hat_t}$인데, 이는 임시 cell state값인데 실제 $c_t$를 구하기 위한 빌드업이라고 생각하면 편하다.

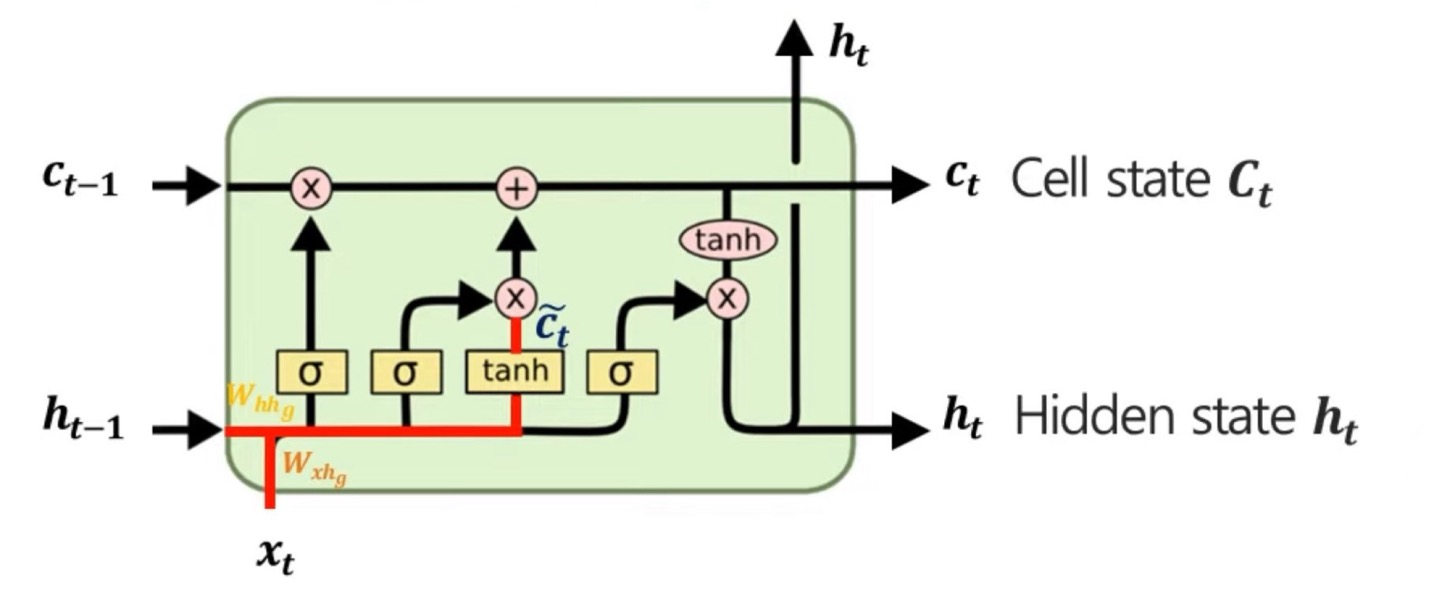
임시 cell state를 구하는 과정인데, 위의 그림을 수학적 수식으로 나타내면 $tanh(W_{xh_g} +W_{hh_g}h_{t-1}+b_{h_g})$이다.
이전 hidden state와 현재 input data를 weighted sum한 값을 tanh를 통해서 -1~1의 값으로 정규화 시켜주어 이전 hidden state와 현재 input data의 정보들을 가지고 있다고 생각하면 된다.

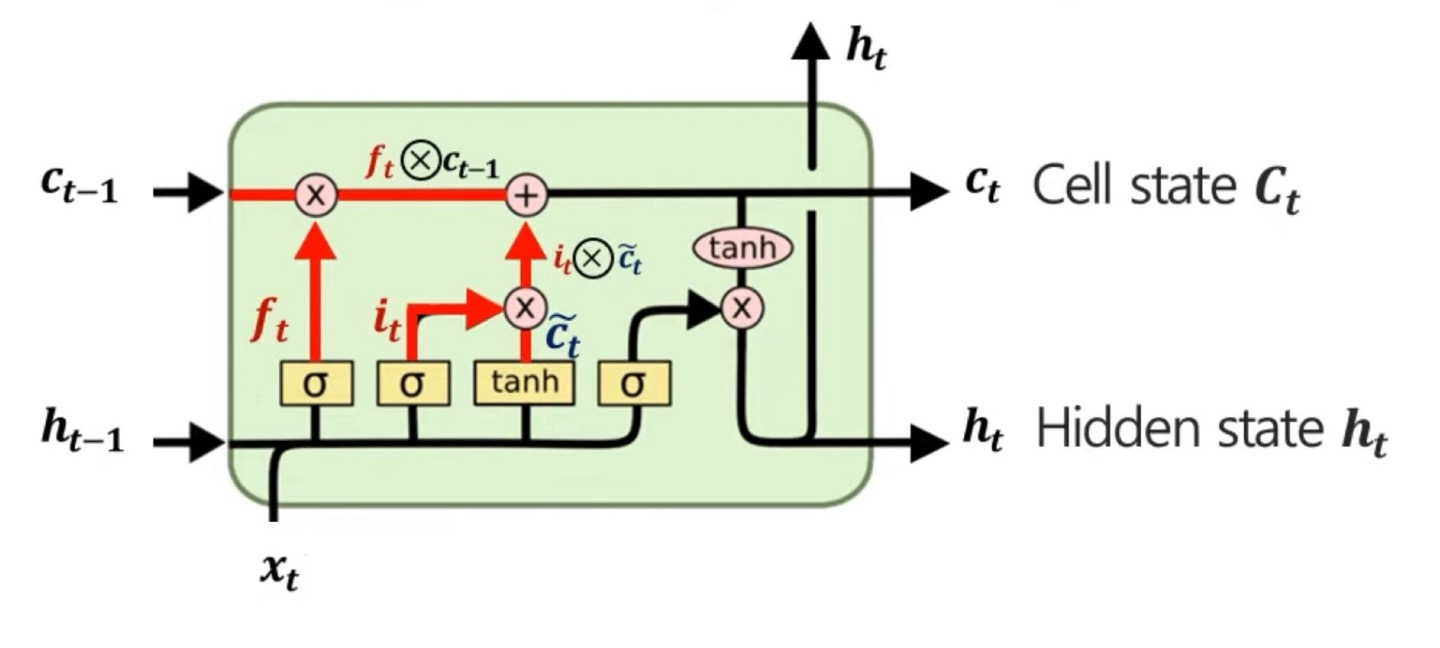
위에서 구하였던 임시 cell state, 이전 시점의 cell state, forget gate, input gate를 통해서 cell state를 만드는 과정인데, 아직 gate에 대해서 설명을 하지는 않았지만 gate는 어떤 정보들이 중요한지에 대한 weight의 역할을 한다고 생각하면 된다.

수학적 수식으로 나타내면, $f_t × c_{t-1} + i_t × c_{hat_t}$인데 여기서 ×는 합성곱(Convolution)이다.(뒤에서 자세히 설명한다.)

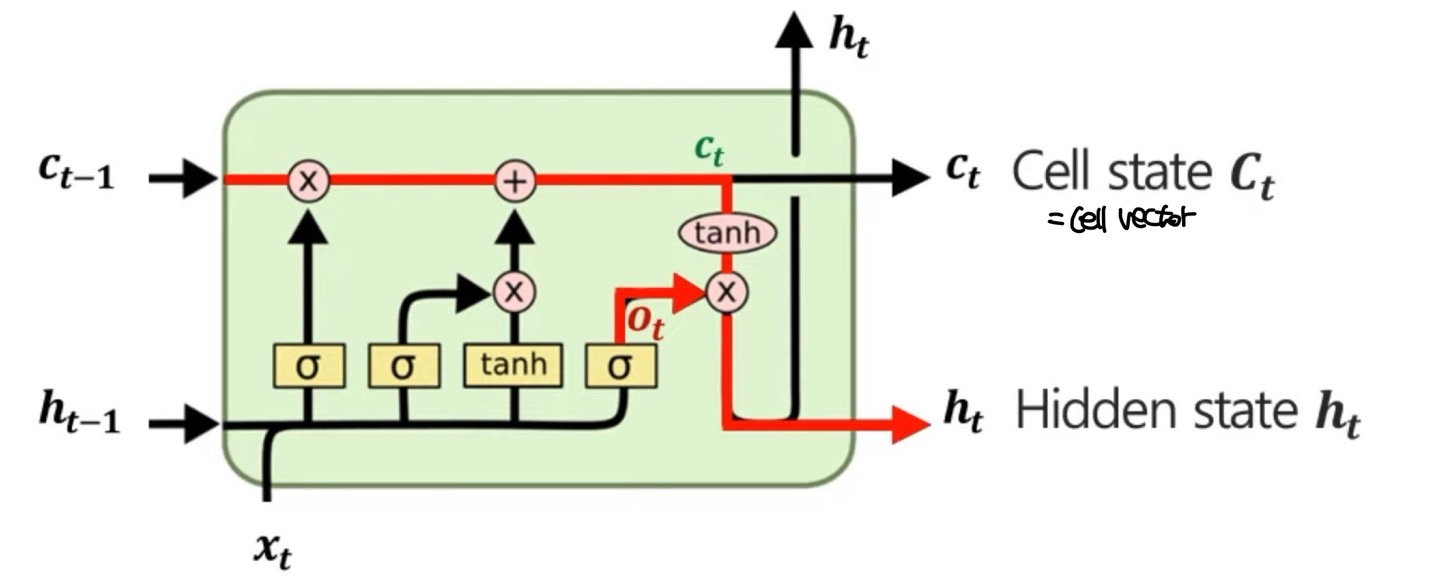
위에서 구한 $c_{hat_t}와 c_t$ 정보들을 이용하여 최종적으로 $h_t$를 구하게 되는데, 여기서의 $o_t$는 output gate로 마찬가지로 weight의 역할을 한다.

수식은 $o_t × tanh(c_t)$이다.

결국에 hidden state를 구하는 과정은 다음과 같다.
1. Gate 계산하기
2. Cell state update하기
3. Hidden state update 하기

그러면 이제 hidden state를 구하는 과정을 차례대로 알아보겠다.

Gate 계산하기

Gate는 위에서 3가지의 종류가 있다고 하였는데, $f_t(forget gate), i_t(input gate), o_t(output gate)$가 있다.

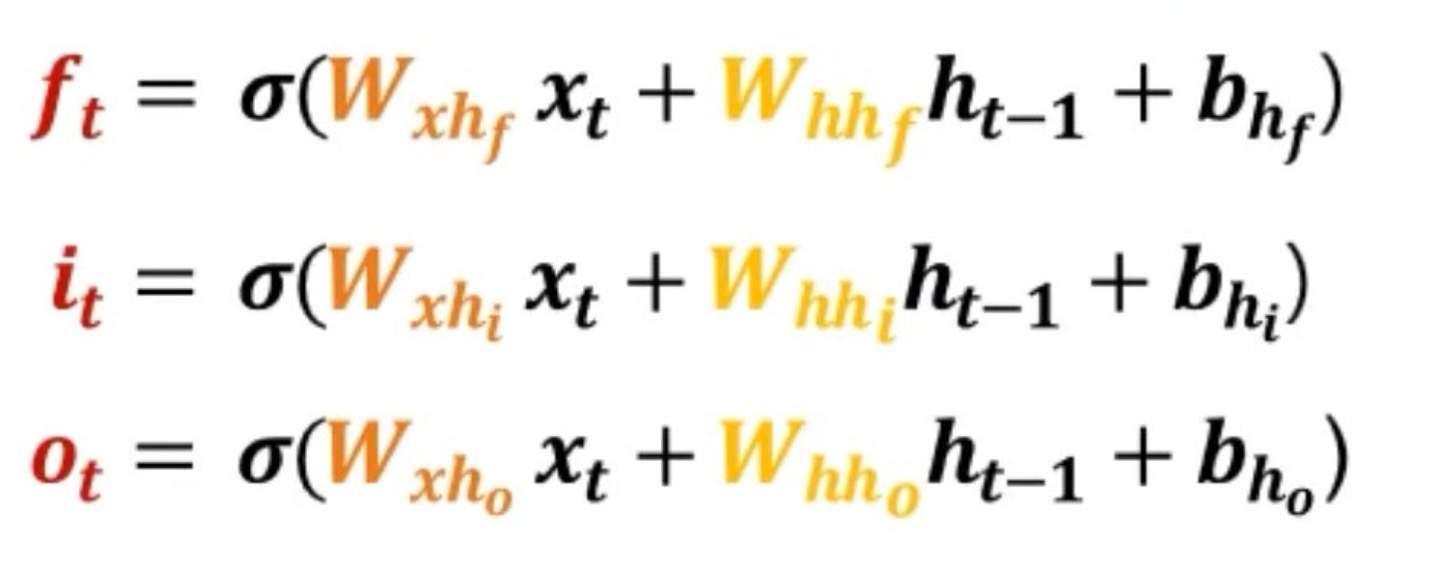수식으로 나타내면 위와 같은데, 종류별로 각각 다른 weight의 값을 지니고 있다는 것을 참고하길 바란다. 또한 σ는 activation function으로 sigmoid function을 이용하는데 0~1사이의 값을 가지고 있으며 이는 얼마나 정보들을 이용할 것인지에 대한 **weight의 역할**을 한다는 것이 매우 중요한 개념이다.

Cell state update 하기

Cell state는 임시 cell state와 현재 시점의 cell state를 구별하여 설명하겠다.

임시 Cell state

임시 cell state는 현재 input과 과거 hidden state의 정보에 대한 정보 요약 vector이며, 수식적으로는 RNN에서 hidden state를 구하는 것과 비슷하다.

$c_{hat_t} = tanh(W_{xh_g}X_t + W_{hh_g} h_{t-1} + b_{h_g})$이다.
tanh를 쓰기 때문에 -1~1사이의 값을 가지고 있다.

Cell state

이제 빌드업은 끝났고 본격적인 Cell state에 대해서 알아보겠다.

먼저 Cell state는 현 시점에 대한 cell state를 update할때 forget gate와 input gate를 활용하게 되는데 앞에서 이는 weight의 역할을 한다고 다시한번 말한다.

먼저 수식은, $C_t = f_t × c_{t-1} + i_t × c_{hat_t}$인데, 이때 ×는 convolution 연산이다.

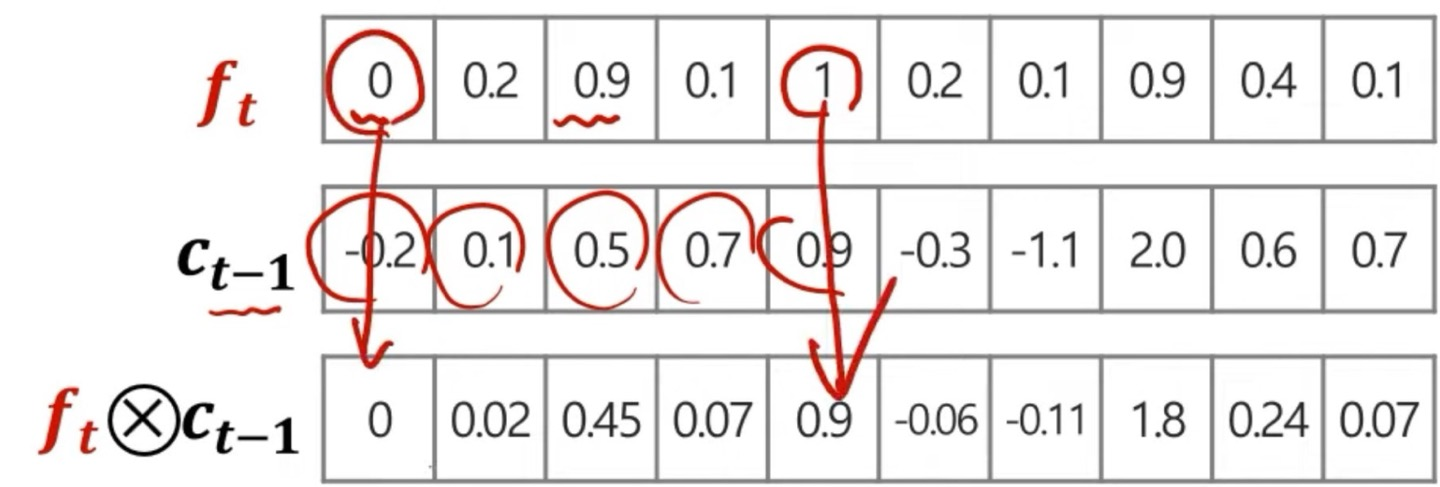
forget gate는 불필요한 과거 정보를 잊기 위한 gate로 $c_{t-1}$에 대한 정보의 weight와 conv연산을 통하여 정보들의 중요성을 따진다.

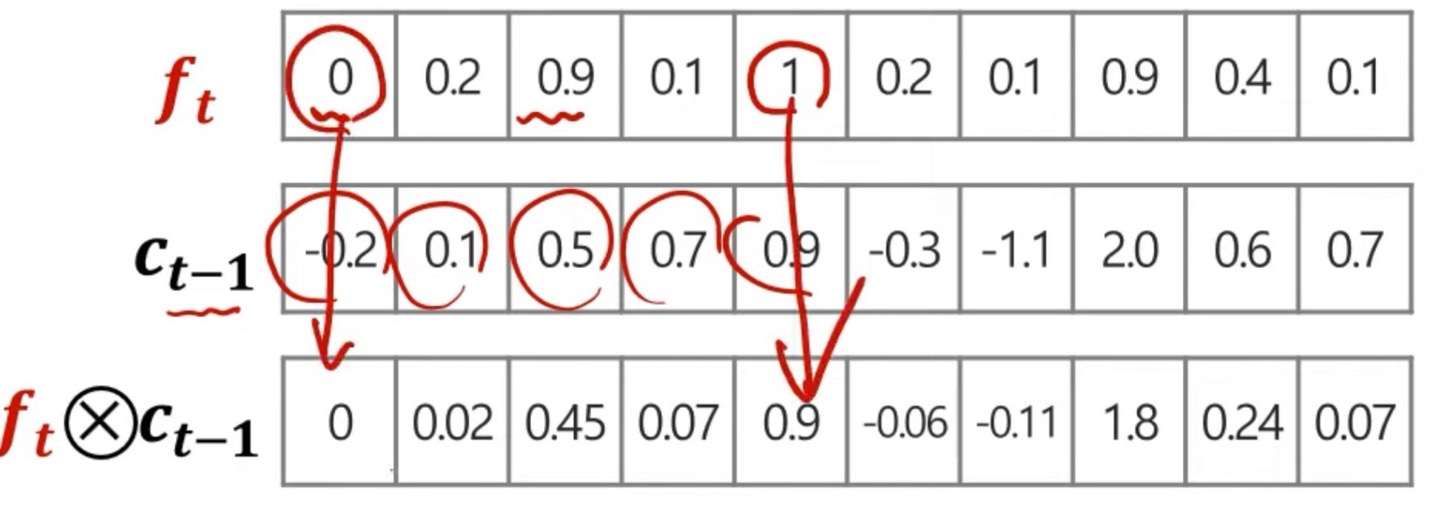
위는 시각적으로 $f_t와 c_{t-1}$의 conv연산을 보여준건데, $c_{t-1}$에 대한 정보 vector를 $f_t$와 mapping되는 weight의 element에 따라 conv연산을 통해 $f_t × c_{t-1}$을 구해준다.

이후, $i_t × c_{hat_t}$를 구하는데 $i_t$는 현재 정보를 기억하기 위한 gate이다.

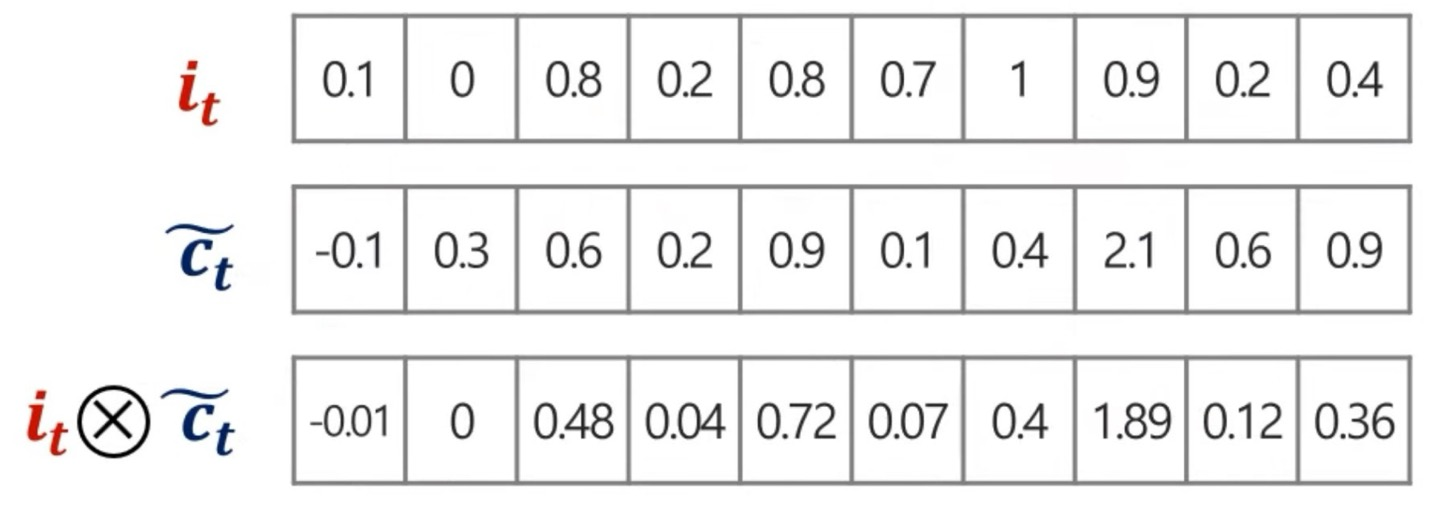
마찬가지로 conv연산을 통해서 $i_t × c_{hat_t}$를 구해주게 된다.

그런 다음 마지막으로 cell state값을 구해주는데 위에서 각각 구한 vector를 element wise로 더해주기만 하면 된다.

뭐 굳이 시각적으로 보게 되면 아래의 그림과 같이 된다.

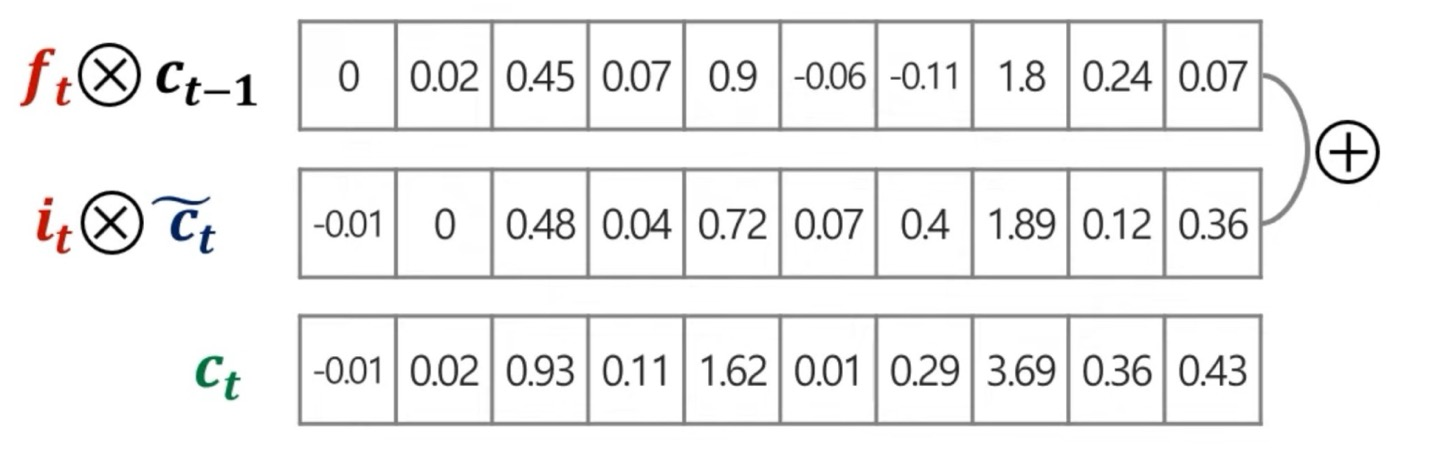
Hidden state update 하기

위의 cell state를 통해서, 우리는 최종적으로 output값을 도출하기 위한 hidden state를 만들어야한다.

즉, output gate를 통해 어떤 정보를 output으로 내보낼지 결정하기 위한 gate로, output을 결정하는데 똑같이 그냥 위와 같이 output을 도출하기 위한 weight라고 생각해주면 된다.

$h_t = o_t × tanh(c_t)$로 구하게 된다.

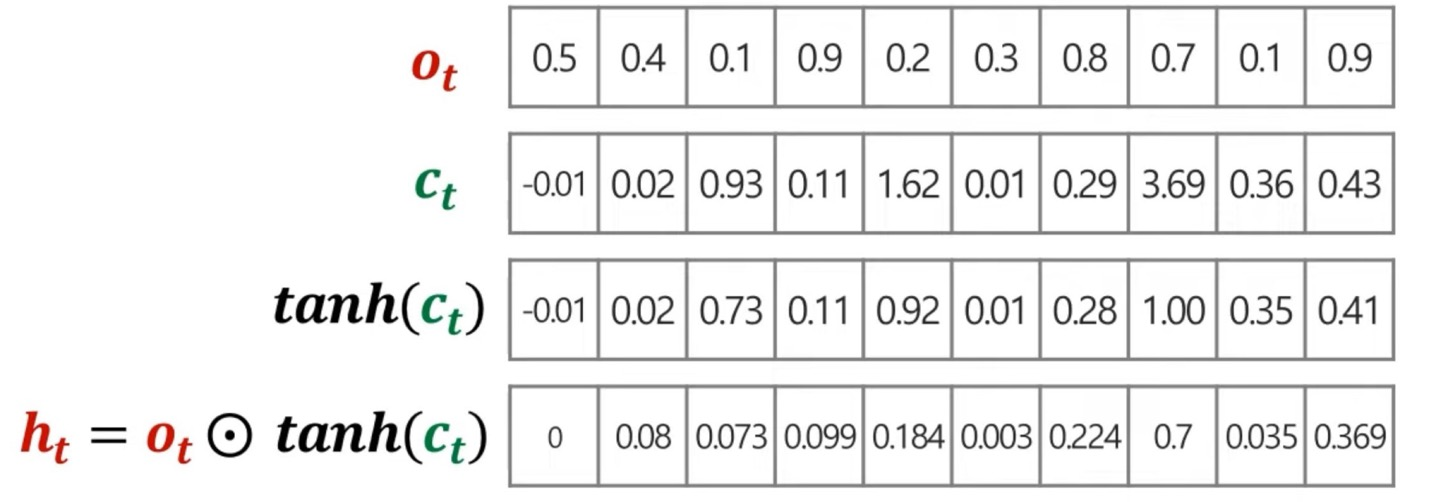
최종적으로 $h_t$를 구하였으니, 예측값인 $f(h_t w_{th})$를 구하여 loss값을 계산하여 weight들을 update할 수 있다.

이때의 weight들은 gate안의 element도 포함되며 backpropagation을 통해서 update가 된다.

---

한계점

이렇게 RNN의 lone-term dependency problem을 해결하였지만, RNN에 비해서 계산해야할 연산이 많으며 $h_t$를 구하는데 오래걸리게 된다.

이를 보완할 GRU라는 모델이 나왔지만, Transformer를 얼른 읽고 싶기 때문에 GRU는 따로 블로그에 쓰지는 않겠다.

---

코드 구현

github 간단한 LSTM모델을 통해서 삼성전자 주가를 예측한 코드입니다.