딥러닝을 위한 수학(선형대수학)

Vector

Matrix는 vector의 연장선이다.
Vector는 크기(Magnitude)와 방향(Direction)을 가지고 있는 화살표이다.

Vector의 크기와 방향을 구하는법은 다음과 같다.(2차원 평면에 있다고 생각했음)

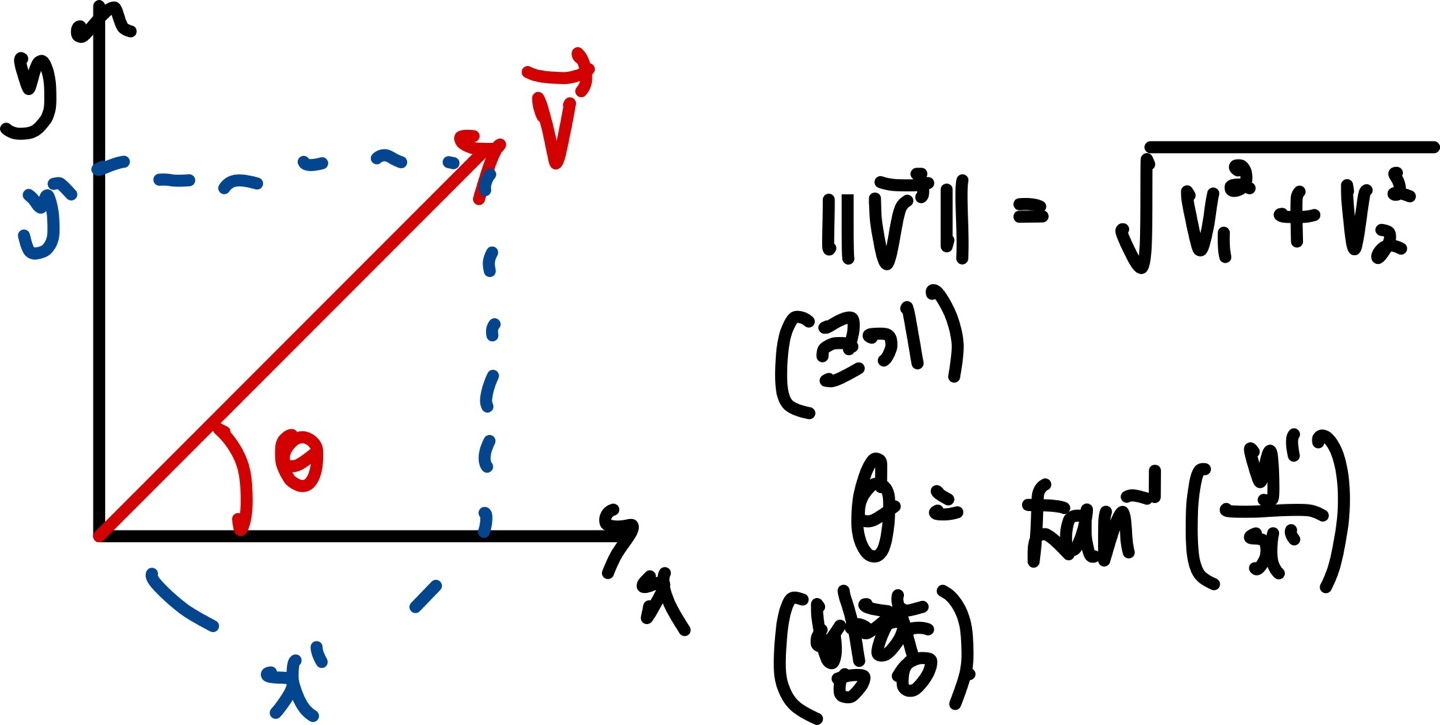
만약 방향만 알고싶다면, 단 Unit vector로 만들면 됩니다.
Unit vector란, 오로지 방향만을 알고싶을때 쓰는 vector입니다.

Unit Vector를 구하는 방법은, Vector에서 Vector의 크기를 나누어주면 됩니다.

• Unit Vector = $\frac{v}{||v||}$

---

L Norm

L Norm을 사용하는 이유는 다음과 같습니다.

• Vector / Matrix 크기 측정
• Normalization
• Optimization

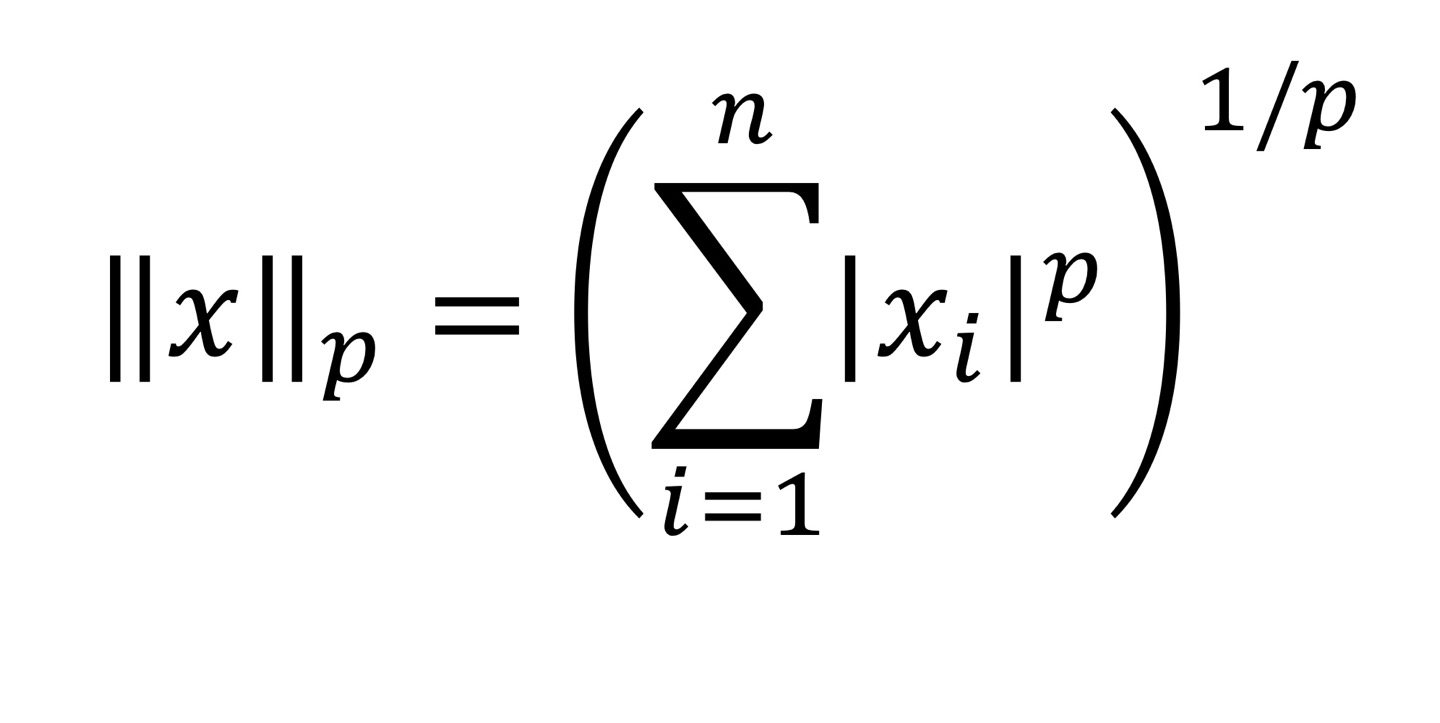
L Norm은 p에 따라서 Norm이 결정됩니다. 제일 많이 쓰는것은 $L_0$ ,$L_1$, $L_2$, $L_∞$가 쓰인다.
$L_∞$은 Vector의 element중에서 절댓값이 가장 큰 값을 고르면 된다.
시그마의 n은 dimension을 뜻합니다.

---

Dot Product(Inner Product)

Dot Product는 한국말로 하면 "내적"이라는 뜻이고, 두 Vector의 유사성을 측정할 때 쓰인다.

Dot Product를 구하는 공식은 ||U|| ||IV|| $\cos(θ)$인데, θ가 만약 0,90을 나타낸다면 특별한 경우가 발생한다.

같은 Vector의 내적은 Vector의 크기인데, $\cos(θ)$에서 θ가 0이므로 1이되고, 90이면 0이므로 값이 0이 된다.
θ(각도)를 알고 싶다면 2번째 있는 식에서 U와V의 크기들만 좌변으로 넘겨주면 각도를 구할 수 있다.

개인적으로 공부할때 Dot Product는 NLP에서 Word Embedding을 할때 단어들의 연관성을 알아보기 위해 쓰인 것을 보았다.

만약 두 개의 Vector가 서로 Orthogonal하고 크기가 각각 1이라면, "Orthonoraml"이라고 말한다. 대표적으로 직교 좌표계의 x축과 y축을 표현하는 basis vector의 $e_x$와 $e_y$는 서로 Orthonormal하다.

이런 Orthonormal vector들은 basis로 사용하면 어떤 물리량을 단위 직교하는 특정 변수들의 합으로 나타낼 수 있는데, 이러한 과정을 Linear Combination이라고 한다.

조금 더 나아가자면, 이러한 Orthonormal한 특정 공간을 만드는 과정을 Gram-Schmidt process라고 한다.

---

Linear Independence

Linear Independence의 정의는 다음과 같습니다.

Vector $x_1$,$x_1$, ... $x_n$이 있을때, 모든 계수가 0인 경우를 제외하고 어떠한 Linear Combination으로도 0을 만들 수 없으면 이 Vector들은 Independent합니다.
만약 그렇지 않다면 dependent합니다

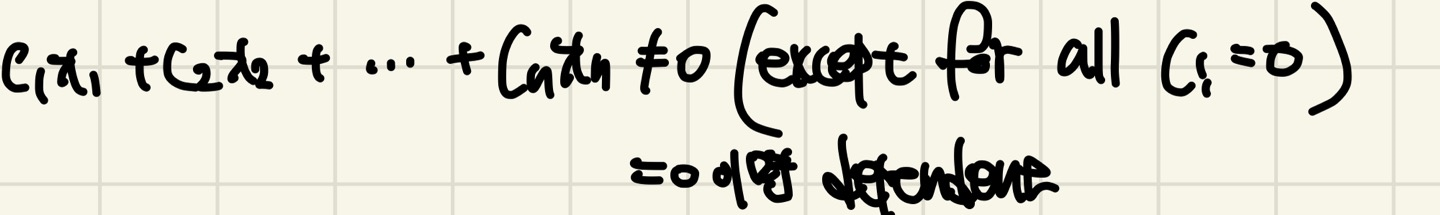
만약 2차원 좌표상에서 v1과 v2가 있고, 다음과 같은 상황이 3개가 있다고 하자.

• 1. 두 개의 Vector가 방향이 같은 경우
• 2. 두 개의 Vector가 방향이 다른 경우
• 3. 어느 하나 0 Vector가 있는 경우

첫번째 Case를 봐보면 두 개의 Vector는 방향은 같지만 크기는 다르다.
그렇다면 v2는 v1의 2배가 되는 Vector라고 생각해보자(v2 = 2v1)
v1과 v2를 Linear Combination을 했을때 식의 변형으로 2v1 - v2 = 0이 된다. 그렇다면 이것은 Linear dependent하다.
Vector의 방향이 같다면 서로 Linear Dependent하게 된다.

두번째 Case는 두 개의 Vector가 방향과 크기가 모두 다르다.
어떠한 Linear Combination으로도 0을 만들 수 없기 때문에(c1,c2가 0인 경우를 제외) 2차원 공간 상의 어던 Vector도 만들어 낼 수 있으므로 Linear Independent합니다.
Vector의 크기와 방향이 다르다면 Linear Independent하게 된다.

세번째 Case는 어느 하나 Vector가 0 Vector가 있다.
v1이 임의의 Vector이고 v2가 0 Vector라고 하자.
식의 조작으로 Linear Combination을 하면 v1의 계수가 0, v2의 계수는 0이 아닌 실수를 넣었을때 값이 0이되므로 Linear Dependent하게 된다.
Vector에 0 Vector가 있다면 Linear Dependent하게 된다.

---

Span and Basis

Span의 정의는 다음과 같다.

Vector $v_1$,$v_1$, ... $v_n$들의 가능한 모든 Linear Combination으로 어떠한 Space를 형성하는 것을 의미한다.
즉, Vector들의 모든 가능한 Linear Combination의 Output Vector들을 하나의 Space에 몰아 넣는 것을 의미한다. 따라서 사용하는 Vector에 따라서 모든 공간을 채울 수도, 혹은 Subspace(부분 공간)만을 채울 수 있다.

Basis 정의는 다음과 같다.

어떤 Space를 Span하면서 그들이 Independent인 Vector들이다.
이것을 Basis(기저)라고 한다.

Basis Vector들의 특징은 서로 Independent하고 Space를 Span 할 수 있다.

대표적인 3차원 공간 $R^3$에서의 Standard Basis는 $\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}$ 이다.
각 Column Vector들을 하나로 합치게 되면 위와 같은 Matrix가 나오게 된다. 이 Matrix의 Null Space는 Zero Vector이며 각 Column Vector들로 3차원 Space 전체를 Span할 수 있게 된다.
특히 이러한 각 Column vector들은 Standard Basis라고 한다.

그렇다면 Vector들이 Basis인지 아닌지 어떻게 판별할 수 있을까?
먼저 Vector들을 하나의 Matrix로 만든 다음, Gauss Elimination을 통해 Matrix를 echelon form Matrix로 만들고 Matrix의 Rank를 알아보면 된다. 만약 Rank가 Matrix의 dimension과 같다면 Matrix의 Column vector들은 서로 Independent하기 때문에 Basis가 될 수 있게 된다.

또한, N dimension을 가지는 $R^N$에 대해 N개의 Vector를 가지고 있을 때 Vector가 Basis가 되기 위해서는 n x n Matrix가 Inverse Matrix가 되어야한다.

이유를 설명하겠다.
$\begin{bmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \\ 2 & 5 & 7\end{bmatrix}$ Matrix가 있다고 하자. 각 Column Vector별로 v1,v2,v3라고 칭하겠다.
v1과 v2의 Linear Combination을 통해 v3가 나오게 된다. 즉, v1과 v2는 Independent 하지만, (v1,v2)와 v3는 Dependent가 된다. 이 뜻은 v1과 v2를 통해 Span을 하게 되면 v3 Vector가 존재하게 된다는 뜻이다.

조금 더 쉽게 설명하면, 위 Matrix를 Transpose 하고 Gauss Elimination을 해보게 되면 $V3^T$는 0 Vector가 나오게 될 것이다.
Inverse Matrix를 구하기 위해서는 Matrix의 Determinant가 0이되면 안되므로 Inverse Matrix가 될 수 없게 된다.

따라서 Matrix의 Determinant값이 0이면 Dependent하게 된다.

---

Dimension

Dimension의 정의는 다음과 같다.

주어진 Span들에 대한 모든 Basis들은 같은 수의 Vector를 가진다.
여기서 Vector의 수가 그 Space의 Dimension을 의미한다.

Dimension은 그 Space가 얼마나 큰 지를 나타내는 지표가 된다.

제가 쓴게 있는데,, 이걸 보면서 이해하시는게 좋을 듯 합니다.

---

Column space and Null space

Four fundamental Subspace는 다음과 같다.

• Column space
• Null space
• Row space
• Left null space

여기서는 Column space와 Null space에 대해서만 자세히 알아보겠습니다.

먼저 각 subspace를 알아보기 전에, Vector space에 대해서 알아보겠습니다.

Vector space

Vector space는 vector의 집합이고, 다음과 같은 조건이 필요로 합니다.

• Vector space내에 임의의 vector v와 w는 그 둘을 더해도 v+w 그 결과가 반드시 같은 vector space에 존재해야 합니다. 덧셈에 대해 닫혀있다고 이야기합니다.

• 또한 임의의 vector v에 스칼라 c를 곱해도 cv가 vector space에 존재해야합니다. 스칼라 곱에 닫혀있다고 이야기합니다.

• 임의의 vector v,w가 상수 c,d에 대해 Linear combination 결과가 반드시 같은 vector에 존재해야 합니다.

Column space

A = $\begin{bmatrix} 1 & 1 & 2 \\ 2 & 1 & 3 \\ 3 & 1 & 4\\ 4 & 1 & 5 \end{bmatrix}$ 가 있다고 하자.

A의 각 Column vector를 독립적으로 보게 되면 모두 $R^4$의 Subspace가 된다. 왜냐하면 Column vector가 4차원이기 때문이다. 그렇다면 Column vector들을 Linear combination하게 되면 $R^4$의 Subspace가 나오게 된다.

이걸 왜 말하냐면, A의 Column Vector들의 Linear combination을 통해 $R^4$전체를 채우지 못하기 때문에 Subspace가 된다는 뜻이다.

그렇다면 A는 $R^4$의 Subspace인데 얼마만큼의 Space를 차지하게 되는 걸까?

A의 Column vector를 v1,v2,v3라고 부르겠다.
v1과 v2의 Linear combination으로 v3를 만들 수 있으니, v1과 v2는 Independent하지만, (v1,v2)와 v3는 Dependent하니 v3는 Space를 만들때 도움을 주지 못하므로 제외 대상이다. 그렇다면 v1과 v2는 어떠한 직선을 의미하는데 v1과 v2의 Linear Combination으로 어떠한 평면을 만들 수 있게 된다.

결론은 A의 Subspace인 Column space는 4차원 space에서 2차원 space인 평면을 정의하는데 그치게 된다.

Null space

Null Space의 정의는 다음과 같다.

Linear Equation Ax = b에서 b가 Zero vector일때 식을 만족시키는 모든 가능한 x에 대한 집합이다.
즉 x에 대한 solution들은 모두 원점(origin)을 지나야한다.

조금 더 깊게 이야기하면 A와 x는 수직의 형태이다. 즉 A라는 평면이 있게 되면 x는 A의 법선 vector가 된다는 의미가 된다.
그렇다면 A라는 Space의 수직인 Null space가 존재한다는 의미가 된다.

---

Linear Equation

Ax = b가 있다.
m : rows(eqautions), n : columns(unknowns)

• m = n : Complete
• m > n : Undercomplete -> 해를 근사화 할 필요 있음.(Regression)
• m < n : Overcomplete -> 무한의 해 가능(추가 Constraint 필요)

Ax자체로 Linear Combination을 뜻하므로 b가 A의 Column Space에 존재해야지 x의 solution이 정해진다.

---

Projection Matrix

Vector Projection은 2개의 Vector중 1개의 Vector를 다른 하나의 Vector에 Projection 시키는 것을 말한다.

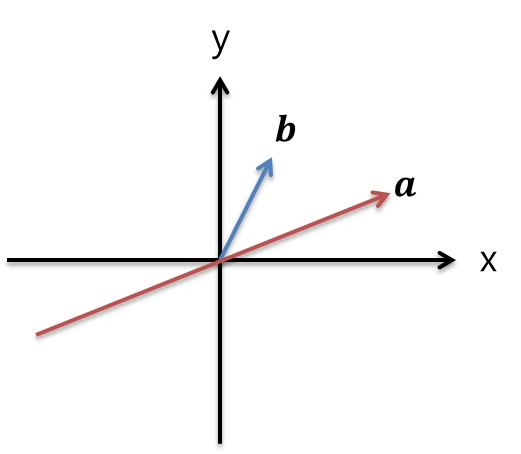
즉, a라는 1차원 Space 어느 점이 b가 가르키는 b의 화살표 끝점과 가장 가까운지를 찾는 것이다. 당연히 b의 끝점에서 a의 Perpendicular 방향으로 선을 그릴때 만나는 점이 가장 가까운 점이다.)

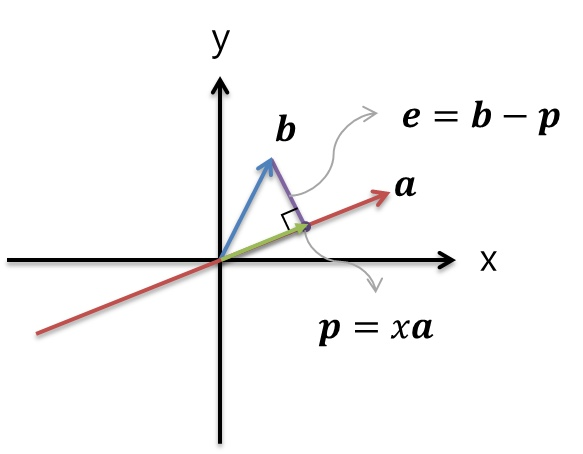
위의 초록색 Vector는 b를 a에 Projection한 Vector이고, p Vector라고 쓰여있다.
이 p Vector는 a의 스칼라 곱 x를 해준 값과 똑같으며 우리는 x를 구하는 것이 목표이다.

보라색 Vector는 Projection 전/후 거리상으로 얼마나 차이가 나는지 나타낸다. a와 Orthogonal하며 p = b - e로 Projection Vector를 구할 수 있게 된다.

위 그림에서 "수직"이라는 용어를 많이 썻는데 수직 하면 떠오르는 것이 있을 것이다.
바로 Dot product 값이 0이라는 것을 이용하면 우리는 x의 값을 구할 수 있게 된다.

그렇다면 a와e가 Perpendicular하므로 a와e를 Dot Product하면 0값이 나오게 된다.

x를 구하는 유도식은 다음과 같다.(p를 구하는 방법은 단순히 a를 양쪽에다가 곱해주면 됌)

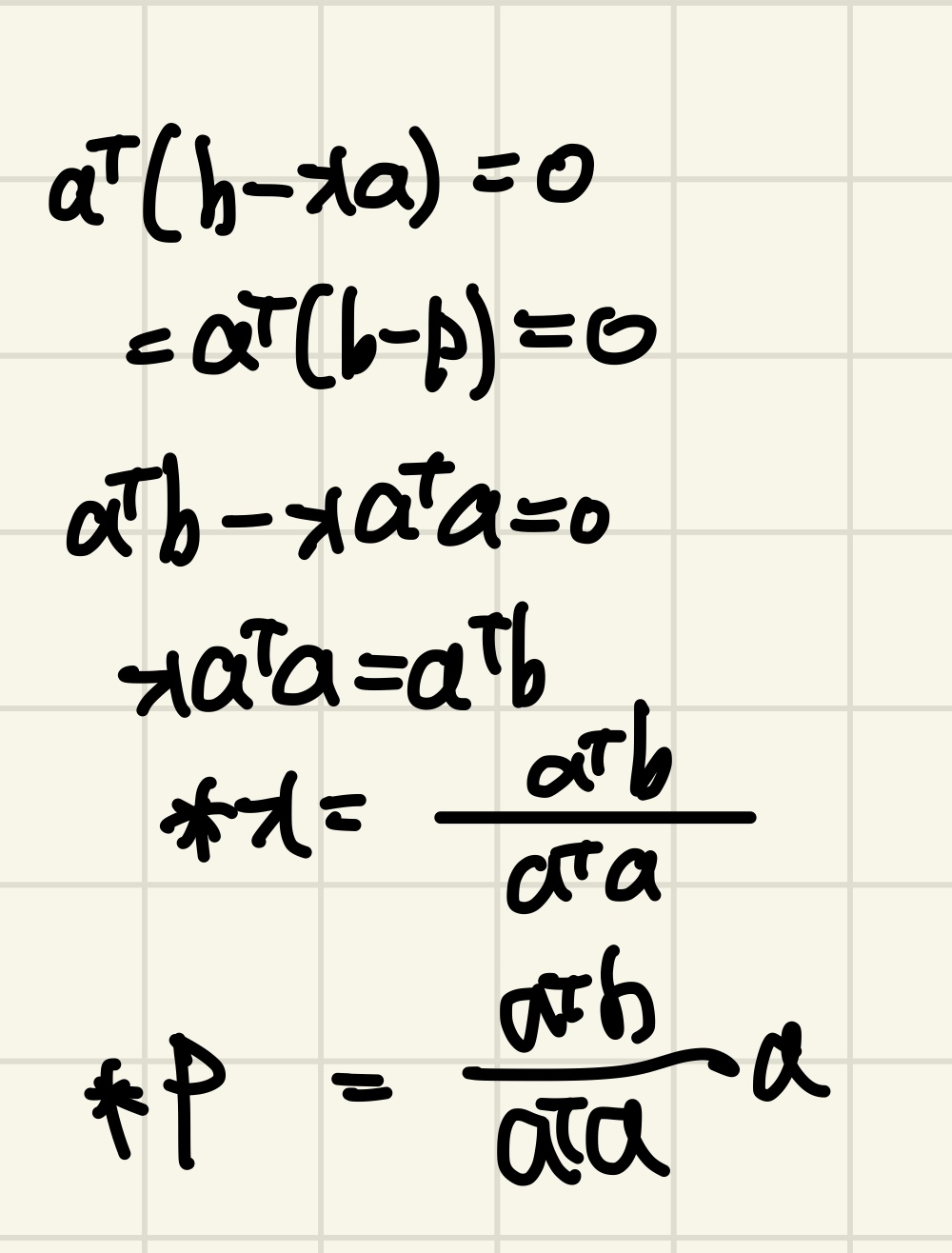
N-Dimensional Vector Projection

위의 2차원 공간에서 Projection을 시키는 것이 아닌 이번엔 N차원 Projection을 시키는 일반화 된 식을 구해보겠습니다.

Ax = b에서 Overdetermined case(Unknowns < Equations)이라면, 해가 없기 때문에 우리는 해에 가장 근삿값을 가지고 있는 x를 찾으려고 한다.

우리가 알고 있는 것은 Ax = b에서 b는 A의 Column space에 존재 해야한다.
따라서 우리는 A의 Column space에서 b와 가장 유사한 Vector를 찾는 것이 목표입니다.

Ax = b가 Column space에 존재해야하는 이유는 다음과 같다. & 위의 b를 생성하는 Linear Combination에서 b를 표현할때 Column Vector를 이용해서 Linear Combination을 했으니 b는 Column space에 있는 것이 당연하다.   조금 더 깊게 이야기하면, x에 어떠한 값이 들어가지 않고 미지수로 남게 된다면 전체 공간을 다 표현할 수 있다. 하지만 Coefficient에 값이 들어가면 vector입니다.

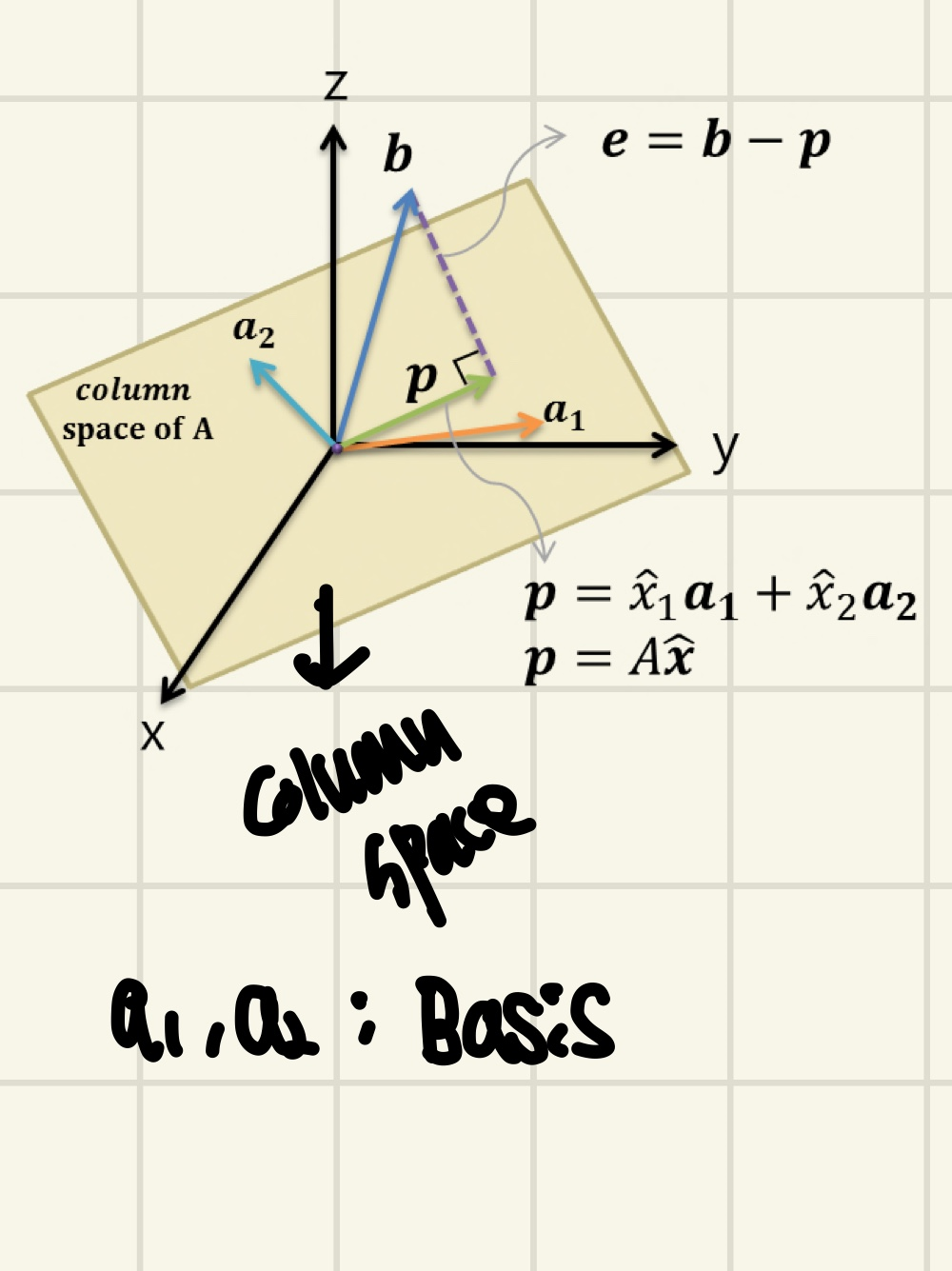
위의 그림을 보면 Column space를 통해 어떤 공간을 만들었고, Vector가 3차원으로 표현되며 Basis는 2개가 된다.
그렇다면 A의 행렬의 크기는 3x2가 되는 것을 알 수 있다. 각 Column vector의 차원은 3이고, Basis의 개수는 2개 이기 때문이다.(A의 Column Vector는 Independent하다고 가정했다.)
Basis가 2개이기 때문에 어떠한 Plane(평면)을 만들게 된다.

b vector는 Column Space Plane에 존재하지 않기 때문에 Ax = b라는 식을 애초에 만족하지 못한다했다. 그래서 b의 근삿값을 얻기 위해 p라는 Projection된 Vector를 얻으려한다.

p = $a_1$$x_1$ + $a_2$$x_2$로 표현이 된다.
그렇다면 p는 Plane위에 존재한다는 것을 알 수 있다. 왜냐?
그 이유는 앞에서와 같다. basis의 Linear Combination을 한 것이기 때문이다.(위의 Column space에 존재해야하는 이유를 보면 이해 가능하다.)

그렇다면 e(b-p)는 plane과 Orthogonal하다. 그렇다면 Dot product가 생각나게 된다.
모든 N차원 Projection의 증명과정은 다음과 같게 된다.

위의 그림을 참고해서 다음 증명과정을 보시면 더욱 이해하는데 편합니다.

---

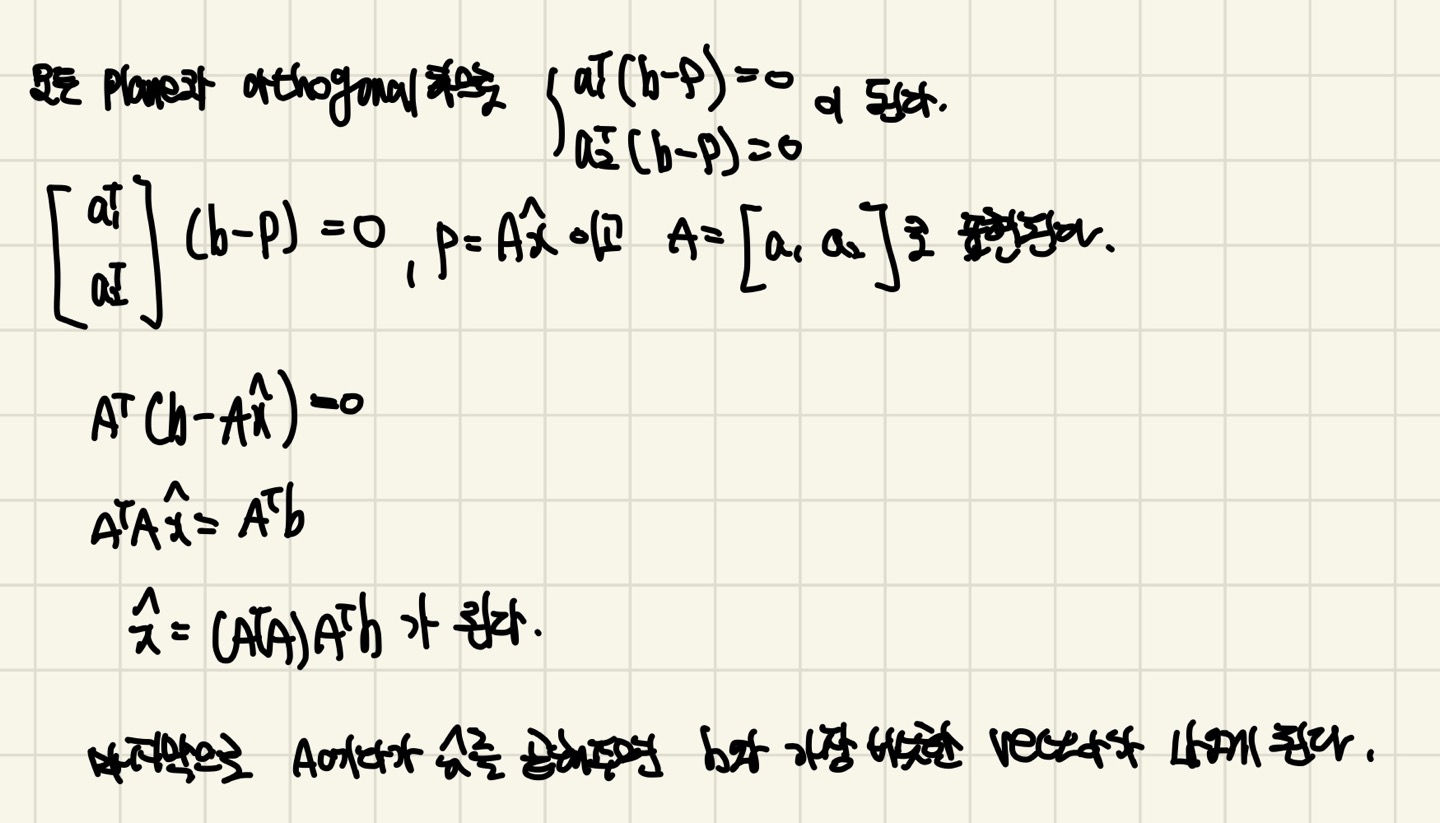
Eigen Vector and Eigen Value

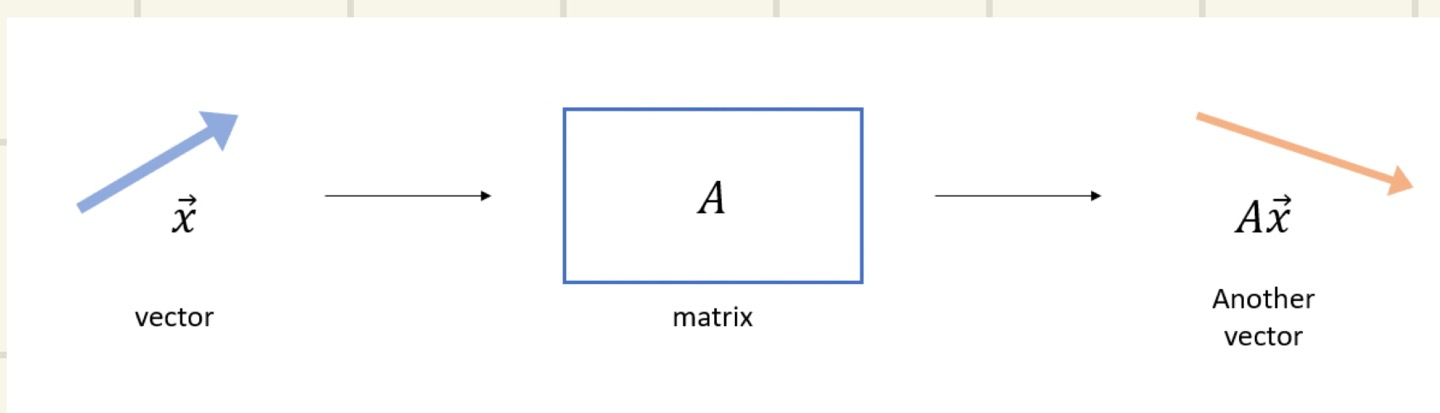
위의 그림은, 기존에 있던 X vector에서 Matrix A를 곱해주었더니 다른 Vector가 나온 것을 볼 수 있다. 그렇다면 Matrix는 Linear Transformation의 역할을 해준다는 것을 알 수 있을 것이다.

X vector와 AX vector는 크기와 방향이 다르다는 것을 위 그림으로 볼 수 있다. 하지만 Linear Transformation을 하더라도 X와 AX는 서로 크기만 바귀고 방향은 바뀌지 않을 수 있다.

예를 한번 들어보겠다.

(Ax = b로 표현)
$\begin{bmatrix} 1 & 2\\ 2 & 1 \\ \end{bmatrix}$ $\begin{bmatrix} 1\\1 \end{bmatrix}$ = $\begin{bmatrix} 3\\3 \end{bmatrix}$ 의 결과가 나온다는 것을 알 수 있다.

b는 x의 vector와 상수배 즉, 방향은 같지만 크기가 3배만 더 큰 Vector라는것을 알 수 있다.
Ax = λx 로 표현할 수 있게 된다. (λ는 상수임)

Eigen Vector와 Eigen Value의 정의는 다음과 같다.

정방행렬 A에 대하여, 0이 아닌 Solution X vector가 존재한다면, λ는 Matrix A의 Eigen value라고 할 수 있다. 이때 X vector는 x에 대응하는 Eigen Vector이다. --> Ax = λx를 설명한 것 이다.

Ax = λx의 식을 변형해보면 (A-λI)x = 0이 된다.
이 식을 만족하기 위해서는 A-λI = 0이 던지, 혹은 x가 0이 되어야하는데 정의에 의해서 x는 0의 값을 가질 수 없다. 그렇기 때문에 A-λI = 0이 되어야하는데 이 식을 Determinant를 구해주면 된다.

다음은 Eigen vector와 Eigen value를 구하는 방법이다.

기하학적으로 다시 설명하자면,

Eigen Vector가 $\begin{bmatrix} 1\\1 \end{bmatrix}$ 일때, Linear Transformation A를 취해주면 방향은 변하지 않고 크기만 배가 커진다는 의미이다.

---

Covariance Matrix

Covariance Matrix는 Data의 구조를 설명ㅇ해주며 feature pairs들의 변동이 얼마만큼이나 함께 변하는가를 Matrix로 나타낸다.

Covariance Matrix가 $\begin{bmatrix} 3 & 2\\2 & 4 \end{bmatrix}$로 있다면, 3은 x축으로 퍼진 정도, 4는 y축, 2는 x,y축 방향으로 퍼진 정도를 의미한다.

Covariance Matrix의 Eigen vector는 Principal axis의 방향을 나타내므로 Data가 어떤 방향으로 variance 되어 있는지 나타내고, Eigen value는 Eigen vector방향으로 얼마만큼의 크기로 Vector space가 늘려지는지를 애기한다.

그렇다면, Eigen value값이 큰 순서대로 Eigen vector를 sorting하면 중요한 순서대로 주성분을 구하는 것이 된다. 왜냐하면 Eigen value값이 클수록 variance를 잘 나타내기 때문이다.

수식적 의미는 다음과 같다.

2변량 이상의 변량이 있는 경우에 여러 개의 두 변량 값들 간의 Covariance를 Matrix로 표현한다.

다음은 Covariance Matrix를 구하는 방법을 나타냈다.

---

선형대수학,, 어렵다....

암튼 읽어주셔서 감사합니다 :>