분류(Classification)
분류는 대표적인 지도학습으로 학습 데이터로 주어진 데이터의 feature와 lael값을 머신러닝 알고리즘으로 학습하고, 새로운 데이터가 주어졌을때 미지의 label을 예측합니다.
다양한 알고리즘에서 앙상블 방법(Ensemble Method)로 분류 알고리즘으로 사용합니다.
앙상블 방법(Ensemble Method)
여러 개의 분류기를 생성하고 그 예측을 결합함으로써 보다 정확한 예측을 도출하는 기법을 말합니다.
즉, 강력한 하나의 모델 대신에 보다 약한 모델 여러 개를 조합하여 더 정확한 예측에 도움을 주도록 하는 방법입니다.
앙상블 기법의 종류에는 크게 3가지가 있습니다.
- 보팅(Voting)
- 배깅(Bagging)
- 부스팅(Boosting)
보팅(Voting)
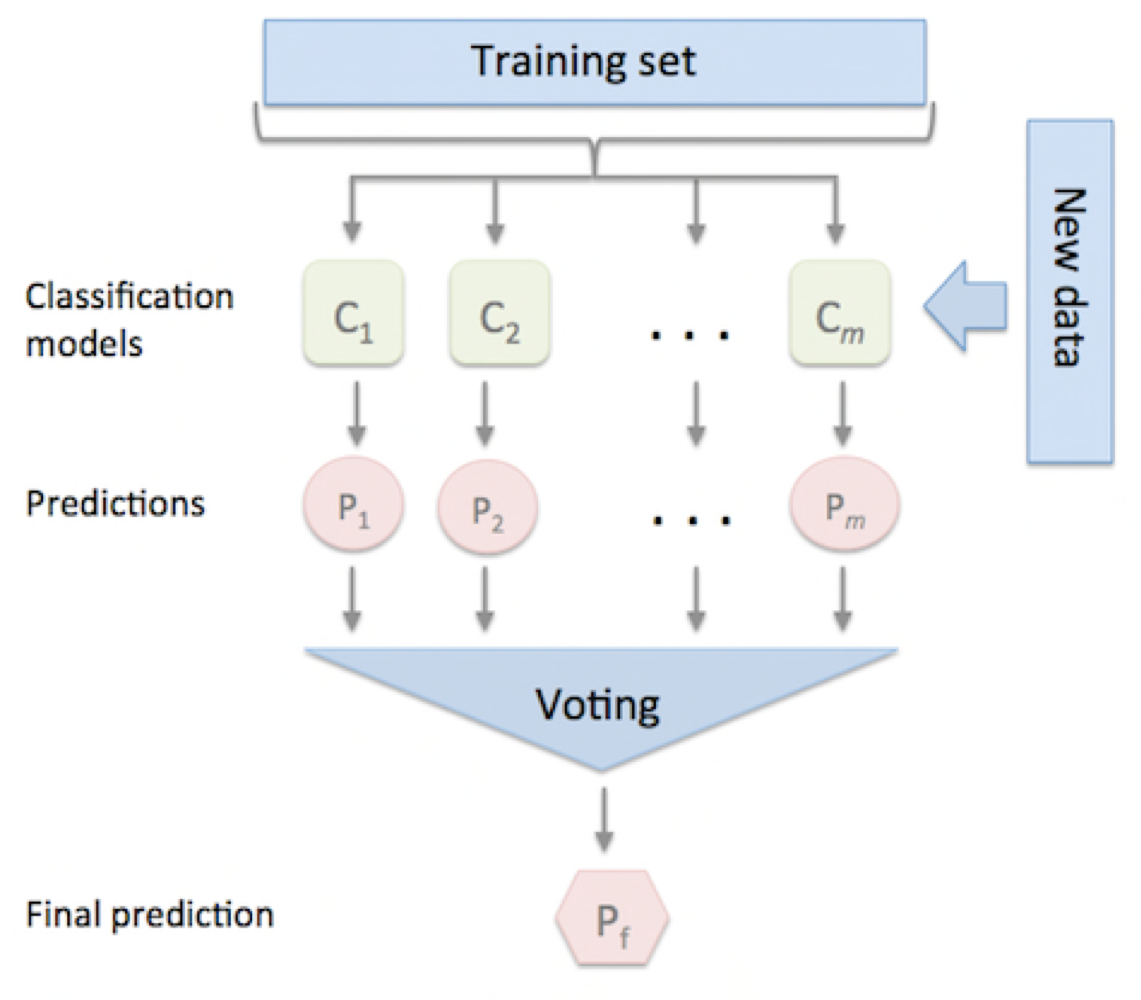보팅은 서로 다른 알고리즘을 가진 분류기 중 투표를 통해 최종 예측 결과를 결정하는 방식입니다.
최종 예측 결과에 따라서 종류가 나뉘어지는데, 하드 보팅(Hard Voting)과 소프트 보팅(Soft Voting)으로 나뉩니다.
하드 보팅은 가장 많은 모델들이 선택한 예측 클래스를 선택합니다.
소프트 보팅은 분류기의 확률을 더해 평균값에서 가장 큰 값(예측값)을 가지는 값을 사용합니다.
배깅(Bagging)
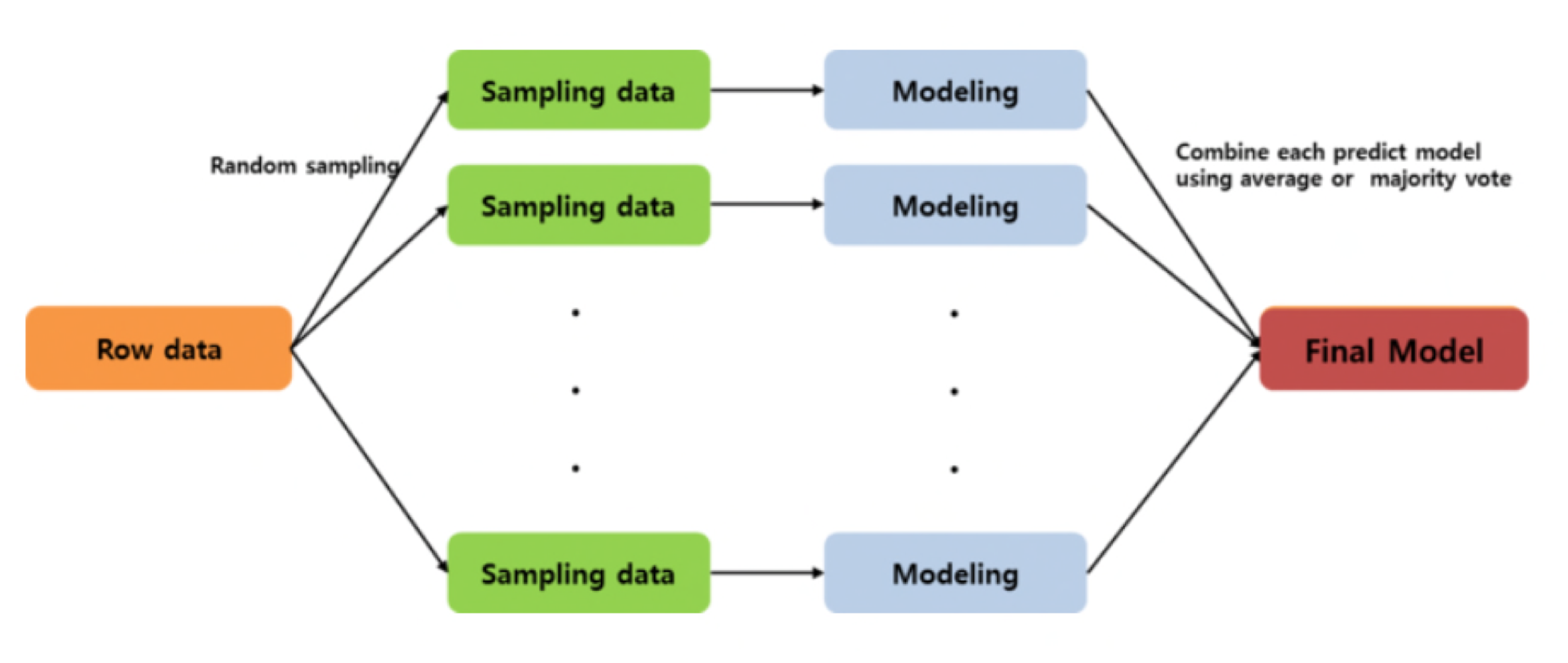배깅은 주어진 데이터에 대해서 여러 개의 부트스트랩(Bootstrap)자료를 생성하고 각 자료를 모델링한 후 결합하여 최종 예측 모형을 산출하는 방식입니다.
여기서 말하는 부스스트랩이란,
- 원본 데이터 셋으로부터 중복을 허용하여 복원 샘플링을 수행하는 방법입니다.
- 작은 데이터 셋에서 표본 추출을 통해 전체 데이터의 특성을 추정하기 위한 방법으로 사용합니다.
- 데이터는 중복이 될 수 있고 선택이 되지 않을 수 있습니다.
말이 조금 어려워서 쉽게 설명하자면 전체 데이터에서 몇개의 데이터만 추출하는 방법을 말합니다.
추출하는 데이터는 중복이 가능하고, 특정 데이터는 선택이 되지 않을 수 있습니다. 이러한 부트스트랩으로 Sampling data를 모으고 각 모델은 데이터를 학습하게 됩니다.
배깅의 모델은 모두 똑같은 알고리즘을 사용하고 과적합을 방지하며 수행속도가 빠르다는 장점이 있습니다.
부스팅(Boosting)
여기서 사진 가져왔습니다.
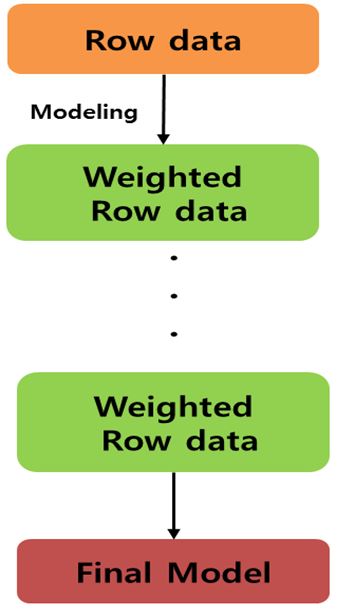
부스팅은 여러 개의 약한 예측 모형을 결합하여서 강력한 예측 모형을 만드는 것 입니다.
순차적으로 약한 학습기를 생성해 나가며, 이전 모델들의 오류에는 더 높은 가중치를 부여하여 다음 모델이 가중치가 조정된 데이터로 학습해 나갑니다.
결정트리(Decision Tree)
결정 트리는 데이터에 있는 규칙을 학습을 통해서 찾아내고 Tree기반의 분류 규칙을 만듭니다. 그래서 이 분류 규칙에 따라서 성능을 크게 좌우합니다.
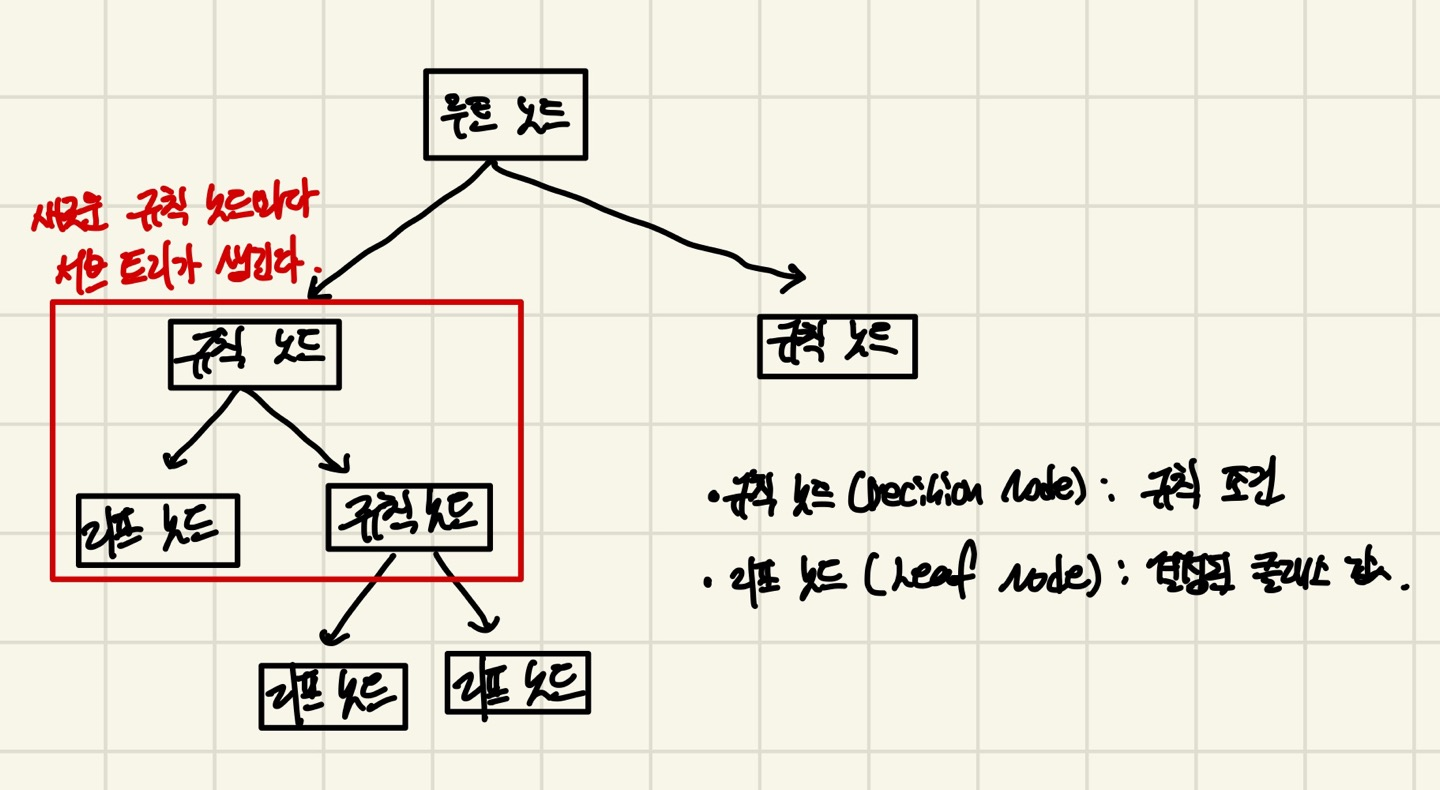
위 결정 트리의 구조를 보면, 새로운 규칙 노드마다 서브 트리가 생기게 되는 것을 알 수 있습니다.
트리의 구조가 깊어질수록 과적합이 일어날 가능성이 높아집니다.
그래서 데이터의 깊이가 깊어지지 않도록 가능한 적은 규칙 노드로 데이터를 분할해야 합니다.
그래서 최대한 정보 균일도가 높은 데이터 세트를 통해서 규칙 노드를 만들어야합니다.
정보 균일도는 한 바구니에 같은 종류의 물건이 많을수록 정보 균일도가 높다고 표현합니다.
정보 균일도를 측정하는 방법은 정보 이득(Information Gain)과 지니 계수가 있습니다.
먼저 부모노드에서 자식노드로 분할 할때 최대한 부모노드의 불순도보다 자식노드의 불손도가 더 적어야합니다.
그래서 불순도를 기준으로 트리를 분할하게 됩니다.
불순도 측정 방법에 따라 정보 이득과 지니 계수로 나뉘게 됩니다.
정보 이득(Information Gain)
정보 이득은 불순도의 측정 방법을 엔트로피(Entropy)를 이용합니다.
엔트로피값이 커질수록 서로 다른 값이 섞여 있고, 작을수록 같은 값이 있는걸로 볼 수 있습니다.
다음 식은 엔트로피 측정 공식입니다.
엔트로피를 측정하고 1 - Entropy를 구해야합니다.
1 - Entropy값이 클수록 좋은 것이고, 작을수록 좋지 않습니다. 그 이유는 Entropy값이 불순도이기 때문에 Entropy값이 작을수록 1 - Entropy값이 커지게 되므로 클수록 같은 값이 섞여 있습니다.
다음은 정보이득을 계산하는 예시 입니다.
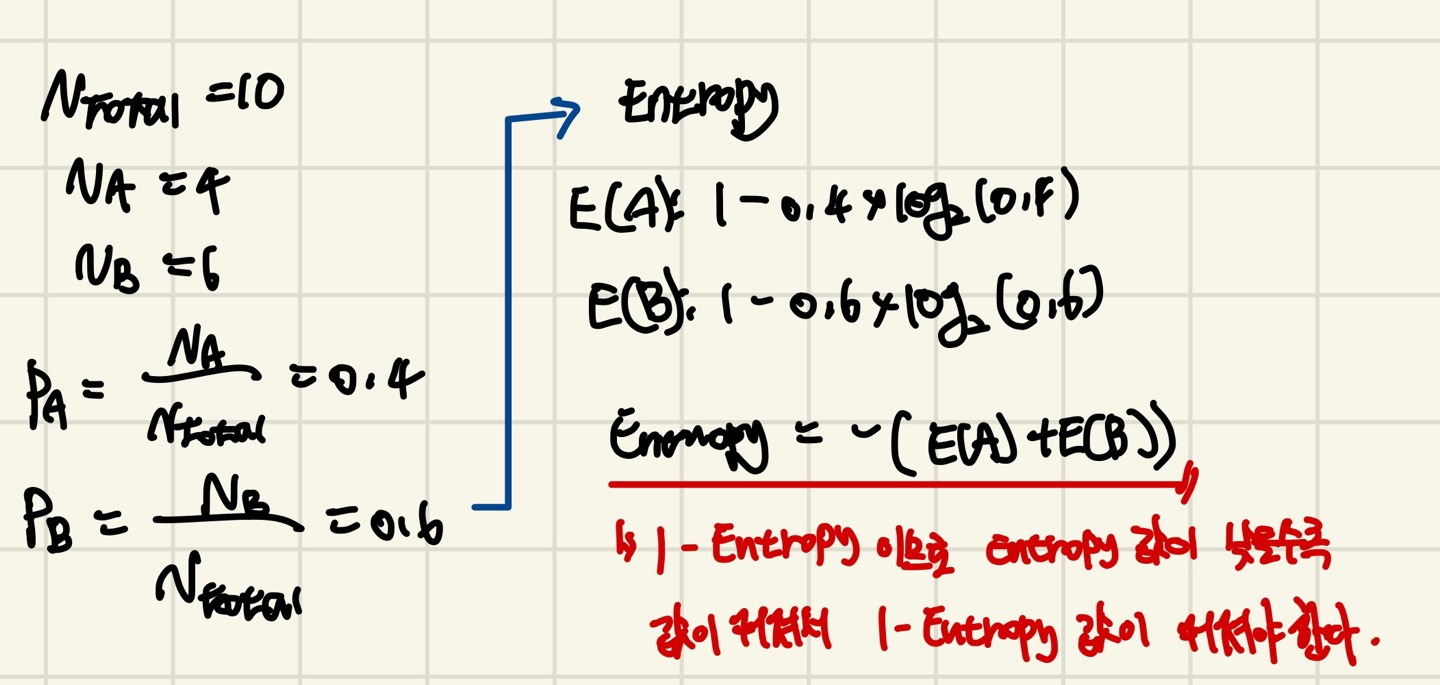
즉, 정보이득 = 1 - Entropy가 되는것이고 정보이득의 값이 큰 값으로 규칙노드를 정의해야 트리가 깊어지지 않으므로 과적합이 일어나지 않습니다.
지니 계수(Gini index)
지니 계수는 지니 계수 값 자체로 불순도를 측정하는 지표로, 데이터의 통계적 분산정도를 정량화해서 표현한 값입니다.
다음은 지니 계수를 구하는 공식입니다.
G값 자체가 불순도, 즉 지니 계수를 의미합니다.
그러므로 지니 계수는 0 ~ 1사이의 값을 지니는데 0에 가까울수록 완전한 순도(즉 값을 값만 있는 모임)이고 1에 가까울수록 최대 불순도(다른 값들도 많이 섞여있는)것을 의미합니다.
다음은 지니 계수를 구하는 예시 입니다.
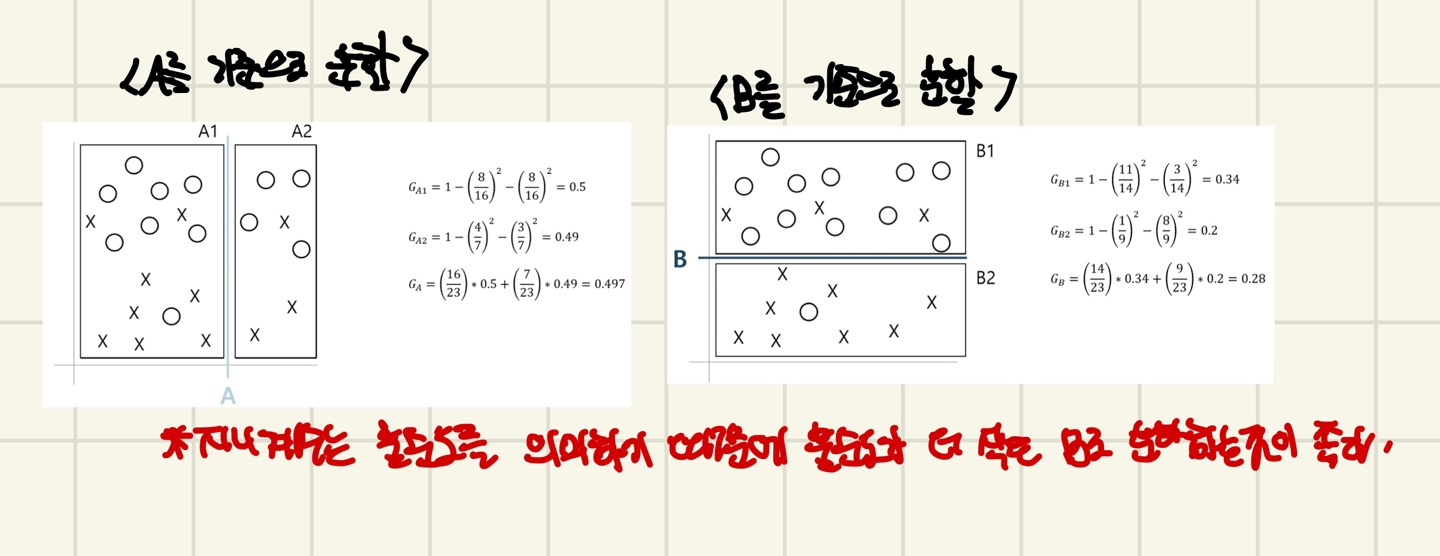
읽어주셔서 감사합니다 :>
