평가

홍성민·2023년 8월 31일

머신러닝

목록 보기

2/5

들어가기에 앞서

머신러닝이 데이터로 학습을 통해 output을 내기 위해서는 데이터 가공/변환, 모델 학습/예측, 평가의 프로세스로 구성이 된다.

성능 평가 지표는 모델이 분류 또는 회귀에 따라 달라집니다.
이 포스트에서는 분류(Classification)에서 이진 분류(Binary Classification)에 대해 다루겠습니다.

분류는 크게 이진 분류와 멀티 분류(Multi Classification)로 나누어집니다.

이진 분류는 크게 긍정/부정으로 2개의 결과 클래스값을 가지고 있고
멀티 분류는 여러 개의 결과 클래스값을 가지고 있습니다.

분류 성능 지표

정확도(Accuracy)

오차 행렬(Confusion Matrix)

정밀도(Precision)

재현율(Recall)

F1 스코어

ROC AUC
이 지표들은 분류에서 매우 중요한 성능 지표이지만, 이진 분류에서 더욱 중요하게 생각되는 지표입니다.

본 포스트는 이진 분류에 대해서 설명합니다.

정확도(Accuracy)

정확도는 직관적으로 모델 예측 성능을 나타내는 평가 지표입니다.

하지만, 이진 분류에서는 데이터의 구성에 따라 ML성능을 왜곡 시킬 수 있어서 정확도 수치만을 보지 않습니다.

예를들어, 단순히 숫자 0과 1을 예측하는 데이터가 100개가 있다고 해보자.
0의 레이블은 90개, 1의 레이블은 10개라고 할때 단순히 100개를 0이라고 예측해도 정확도가 90%가 나오는 지경에 이르기 때문에 데이터의 구성에 따라 ML 모델의 성능을 왜곡할 수 있습니다. 그래서 정확도 수치만을 보고 모델의 성능을 판단하지 않는 것 입니다.

밑의 코드는 MNIST에서 3의 숫자가 나오면 True, 3의 숫자가 아니라면 False를 예측 수행하지만, Classifier객체에서 fit이 비어있으므로 Estimator는 학습을 수행하지 않고 단순히 predict값으로 False값만을 반환한다.

from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.base import BaseEstimator # 개발자가 Estimator를 만들 수 있음
from sklearn.metrics import accuracy_score
import numpy as np
import pandas as pd

class Classifier(BaseEstimator):
  # 학습 수행 x
  def fit(self, X, y):
    pass

  # 예측은 단순히 0만 return  
  def predict(self, X):
    return np.zeros((len(X), 1))

digits = load_digits()

# 3인 값만 True, 나머지(0,1,2,4,5,6,7,8,9)는 False
label = (digits.target == 3).astype(bool)

train_data, target_data, train_label, target_label = train_test_split(digits.data, label, random_state = 0) # test_size 디폴트 값은 0.25

myclassifier = Classifier()

myclassifier.fit(train_data, train_label) # 학습 수행하는데 학습하는게 없음
prediction = myclassifier.predict(target_data) # 테스트 데이터로 예측 수행(target_data의 길이만큼 False로 채워진 배열 반환)

print('불균형한 데이터 확인')
print(pd.Series(target_label).value_counts()) # 테스트 데이터의 레이블의 불균형한 데이터 확인
print()

print('정확도 확인 :', accuracy_score(target_label, prediction)) # False값을 450개중에 405로 했기 때문에 당연히 45 / 405 = 0.9가 나올 수 밖에 없다.

target_data의 길이만큼 False값으로 채워진 배열이 반환된다.

target_label의 분포도를 보면 450개중 405개가 False, 45개가 True값이므로 정확도는 45 / 450인 0.9의 정확도가 나오게 됩니다.

오차 행렬(Confusion Matrix)

오차 행렬은 이진 분류의 예측 오류가 얼마인지와 더불어 어떠한 유형의 예측 오류가 발생하고 있는지를 함께 나타내는 지표입니다.

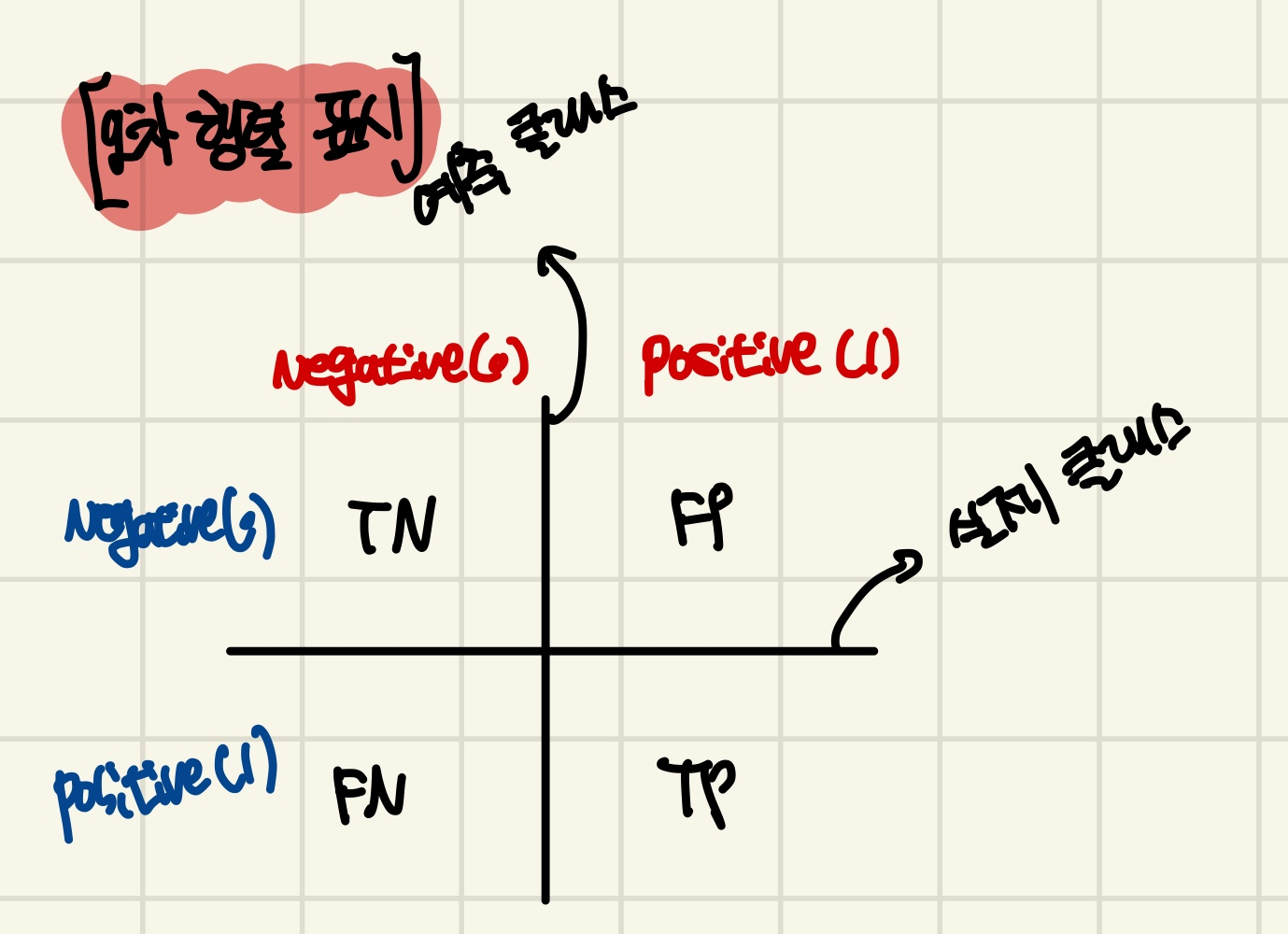
오차 행렬을 해석할때 예측 클래스를 읽고 실제클래스를 읽어주면 됩니다.

예를들면, TN은 예측 클래스가 Negative이고 실제 클래스도 Negative한 것 입니다.

TN : 예측값을 Negative 값 0으로 예측하고 실제 값도 Negative 값 0
FP : 예측값을 Positive 값 1으로 예측하고 실제 값은 Negative 값 0
FN : 예측값을 Negative 값 0으로 예측하고 실제 값은 Positive 값 1
TP : 예측값을 Positive 값 1으로 예측하고 실제 값도 Positive 값 1

from sklearn.metrics import confusion_matrix # 오차 행렬 수행

print(confusion_matrix(target_label, prediction))
# 오차 행렬 결과 값 : [[405,0],
					[45, 0]]

여기서 오차 행렬 결과 값을 보시면 405는 TN, 45는 FN으로 우리는 전부 다 예측값은 Negative로 예측했으니 TP와 FP는 0입니다.

이러한 오차행렬을 통해 우리는 Classifier 성능의 여러 면모를 판단할 수 있는 기반 정보를 제공합니다.
주요 지표인 정확도, 정밀도(Precision), 재현율(Recall) 값을 알 수 있습니다.

정확도 = 예측값과 실제값이 맞는 경우의 수 / 모든 데이터의 수 이므로 (TN + TP) / (TN + TP + FP + FN)이 오차행렬안에서의 공식이 됩니다.

이러한 비대칭한 데이터 세트에서 Postivie에 대한 예측 정확도를 판단하지 못한 채 Negative에 대한 예측 정확도만으로도 분류의 정확도가 매우 높게 나타나는 수치적인 판단을 일으키게 됩니다. 그렇기 때문에 데이터의 균형이 매우 중요합니다.

정밀도(Precision)과 재현율(Recall)

정밀도와 재현율은 Positive 데이터 세트의 예측 성능에 좀 더 초점을 맞춘 평가 지표입니다.

정밀도와 재현율의 공식은 다음과 같습니다

정밀도 = TP / (FP + TP)
재현율 = TP / (FN + TP)

정밀도(양성 예측도)

정밀도는 공식을 보면 알겠지만, 예측 값을 Positive로 한 대상 중에 예측과 실제 값이 Positive로 일치한 데이터의 비율을 말합니다.

FP + TP는 Positive로 예측한 데이터의 모든 건수이고, TP는 예측 값이 Positive인데 실제 값도 Positive로 일치한 데이터 건수입니다.

정밀도는 실제 Negative 음성 데이터를 Postive로 잘못 판단하면 안될때 사용하는 중요한 지표 입니다.

재현율(민감도, TPR(True Positive Rate))

재현율은 실제값이 Positive인 대상 중에 예측과 실제 값이 Positive로 일치한 데이터의 비율을 말합니다.

FN + TP는 실제 값이 Positive인 모든 건수이고, TP는 예측 값이 Positive인데 실제 값도 Positive로 일치한 데이터 건수입니다.

재현율은 실제 Positive 양성 데이터를 Negative로 잘못 판단하면 안될때 사용하는 중요한 지표 입니다.

정밀도와 재현율은 TP를 높이는데 힘을 쓰지만, 정밀도는 FP 재현율은 FN을 낮추는데 힘을 씁니다.
정밀도와 재현율은 서로 보완적인 지표로 분류의 성능을 평가하는데 사용이 되고, 한쪽은 높고 한쪽은 낮은 경우는 바람직하지 않으나 서로 모두 높은 수치를 얻는 것이 가장 좋은 성능을 얻을 수 있습니다.

아래의 코드는 정확도, 정밀도, 재현율을 구하는 코드입니다.

from sklearn.metrics import accuracy_score, precision_score, recall_score, confusion_matrix # precision_score : 정밀도, recall_score : 재현율 수행
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression # 로지스틱 회귀 수행
from sklearn.preprocessing import LabelEncoder
import pandas as pd

# 결측치 제거
def noNaN(df):
  df.fillna({'Age' : df['Age'].mean(), 'Cabin' : 'N', 'Embarked' : 'N', 'Fare' : 0}, inplace = True)

  return df

# 머신러닝 알고리즘에서 불필요한 피처 제거 (object자료형 제거)
def drop_features(df):
  df.drop(['Name','Ticket','PassengerId'],axis = 1, inplace = True)

  return df

# 인코딩
def labelEncode(df):
  df['Cabin'] = df['Cabin'].str[:1]
  features = ['Cabin','Sex','Embarked']

  for feature in features:
    le = LabelEncoder()
    le.fit(df[feature])
    df[feature] = le.transform(df[feature])

  return df

# 전처리
def transform_feature(df):
  df = noNaN(df)
  df = drop_features(df)
  df = labelEncode(df)

  return df

# 정확도, 정밀도, 재현율 구하기
def MutliFunction(target_label, prediction):
  confusion = confusion_matrix(target_label, prediction)  # 오차 행렬
  accuracy = accuracy_score(target_label, prediction) # 정확도
  precision = precision_score(target_label, prediction) # 정밀도
  recall = recall_score(target_label, prediction) # 재현율

  print('오차행렬')
  print(confusion)
  print()

  print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f}'.format(accuracy, precision, recall))


titanic_df = pd.read_csv('titanic.csv')

label = titanic_df['Survived']
train = titanic_df.drop(columns = ['Survived'], axis = 1)
train = transform_feature(train)

train_data, target_data, train_label, target_label = train_test_split(train, label, test_size = 0.2, random_state = 11)

lr_clf = LogisticRegression(solver = 'liblinear')

lr_clf.fit(train_data, train_label)
prediction = lr_clf.predict(target_data)

MutliFunction(target_label, prediction)

정밀도/재현율 Trade-Off

정밀도/재현율 Trade-Off란 정밀도와 재현율은 서로 상호보완적인 관계이기 때문에 어느 한쪽이 커지면 다른 한쪽은 작아지는 현상이 일어나는 것을 의미합니다.

분류하려는 업무 특성상 정밀도 또는 재현율이 특별히 강조되어야 할 경우에는 분류의 결정 임계값(Threshold)를 조정하여 정밀도 또는 재현율을 높일 수 있습니다.

일반적인 이진 분류에서는 임계값을 0.5로 정하고 만약 0.5보다 크면 Positive, 작으면 Negative로 결정합니다.

밑의 코드는 개별 클래스의 예측 확률을 반환하는 pred_proba()메서드를 이용해서 predict()와 무슨 연관이 있는지 알아보는 코드입니다. 여기서 임계값은 0.5 입니다.

이러한 방식으로 계속해서 Trade-Off에 대해서 설명하겠습니다.

import numpy as np

prediction_proba = lr_clf.predict_proba(target_data) # predict_proba()는 이진 분류에서 Positive와 Negative의 확률을 나타내준다. 첫번째 열은 Negative, 두번째 열은 Positive, 반환값은 2D numpy 
predicition = lr_clf.predict(target_data) # predict로 예측 수행해보기

print('pred_proba 데이터 크기 : ', prediction_proba.shape)
print('pred_proba 앞의 3개 데이터만 출력해보기')
print(prediction_proba[:3])

# 확률과 예측값 서로 병합해서 결과 값 살펴보기
prediction = np.array(prediction).reshape(-1,1) # 1차원에서 2차원으로 고쳐주기
result = np.concatenate([prediction_proba, prediction], axis = 1)

print('result의 앞의 3개 데이터만 출력해보기')
print(result[:3]) # pred_proba 메서드로 확률을 추출하고 predict를 통해서 가장 높은 확률을 가지는 열의 인덱스를 출력하는 것을 알 수 있다.

이 코드는 임계값에 따른 오차행렬,정확도,정밀도,재현율을 출력합니다.(앞의 코드와 이어져있습니다.)

from sklearn.preprocessing import Binarizer # 임계값 정하기

# 임계값
thresholds = [0.5, 0.4]

prediction_proba_1 = prediction_proba[:, 1].reshape(-1, 1) # Positive값만 추출하기, Binarizer는 fit,predict로 2D 받음

for threshold in thresholds:
  binarizer = Binarizer(threshold = threshold).fit(prediction_proba_1) # 임계값 설정하고 학습 수행
  prediction = binarizer.transform(prediction_proba_1)

  print(f'임계값 {threshold}일때 정보')
  print(MutliFunction(target_label, prediction))
  
임계값 0.5일때 정보
오차행렬
[[108  10]
 [ 14  47]]

정확도: 0.8659, 정밀도: 0.8246, 재현율: 0.7705
None
임계값 0.4일때 정보
오차행렬
[[97 21]
 [11 50]]

정확도: 0.8212, 정밀도: 0.7042, 재현율: 0.8197

임계값이 낮아질수록 정밀도는 내려가고 재현율은 올라가는 것을 볼 수 있습니다.

이는 Threshold값이 작을수록 Positive로 예측하는 숫자가 증가하므로 FP,TP는 올라가므로 Negative로 예측하는 TN,FN은 줄어들게 됩니다.

다음 코드는 재현율과 정밀도의 서로 상호보완적이라는 것을 증명하는 코드입니다.

from sklearn.metrics import precision_recall_curve # 재현율/정밀도 구해줌
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
%matplotlib inline

def picture(target_label, pred_proba):
  precisions, recalls, thresholds = precision_recall_curve(target_label, pred_proba) # 정밀도,재현율,임계값을 차례로 반환. 이때의 임계값은 함수자체적으로 임계값을 정한 값들이다.

  thr_end = thresholds.shape[0] # 임계값의 길이
  
  plt.figure(figsize = (8,6)) # 사진 크기 조정
  plt.plot(thresholds, precisions[0 : thr_end], linestyle = '--', label = 'Precision') # 정밀도 변화 그리기
  plt.plot(thresholds, recalls[0 : thr_end], label = 'Recalls') # 재현율 변화 그리기

  start, end = plt.xlim() # x값의 처음과 끝을 반환
  plt.xticks(np.round(np.arange(start, end, 0.1), 2)) # x값 범위 정하기
  plt.gca().get_yaxis().get_label().set_rotation(0)
  plt.xlabel('Thresholds') # x축 이름
  plt.ylabel('Precision and Recall value', labelpad = 50) # y축 범위주기

  plt.legend()
  plt.grid()

  plt.show()

picture(target_label, prediction_proba_1)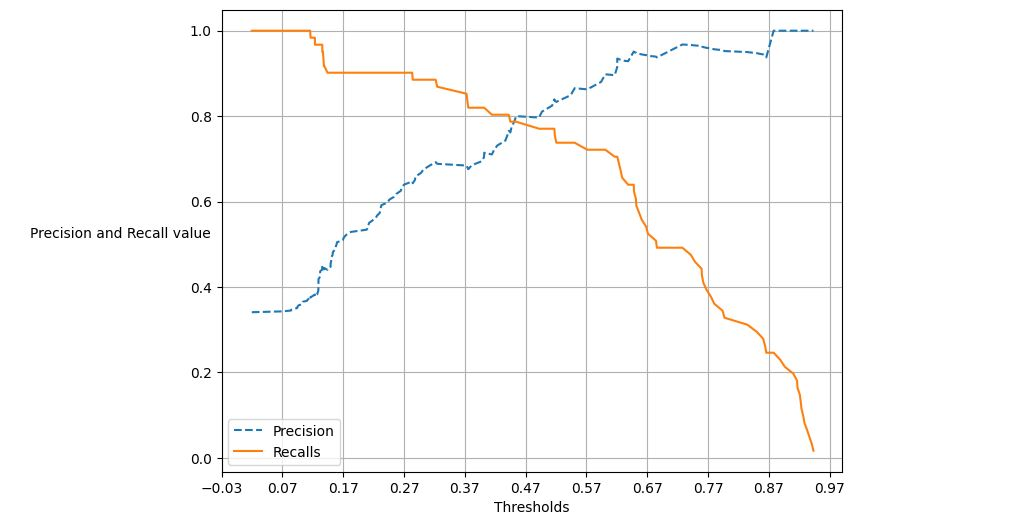

출력을 보시면 재현율이 높을때는 정밀도가 낮고, 재현율이 낮을때는 정밀도가 높습니다.

서로의 교점(임계값)이 최적의 재현율과 정밀도 값을 얻을 수 있습니다.

F1 Score

F1 Score는 정밀도와 재현율이 어느 한족으로 치우치지 않을때 높은 값을 가집니다.

밑의 공식은 F1 Score를 계산하는 공식입니다.

밑의 코드는 f1_score를 구하는 코드입니다.

from sklearn.metrics import f1_score # f1 score를 계산

f1 = f1_score(target_label, prediction)
print('f1 score :', np.round(f1,2))

ROC곡선과 AUC

ROC곡선과 이에 기반한 AUC 스코어는 이진 분류의 예측 성능 측정에서 중요하게 사용되는 지표입니다.

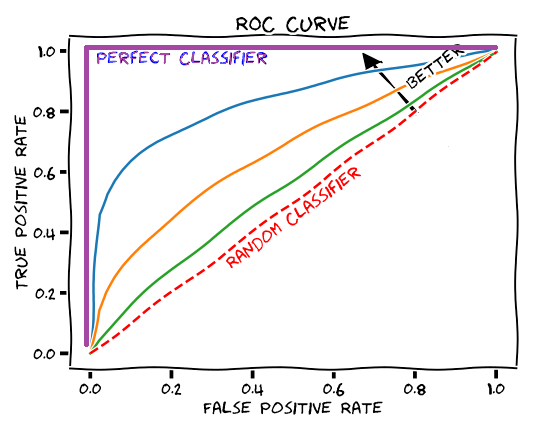
x축은 TPR를 의미합니다. TPR은 실제값이 Positive일때 예측값도 Positive를 나타내는 비율이므로 재현율, 즉 민감도(Sensitive)를 의미합니다.

y축은 FPR를 의미합니다. FPR은 실제값이 Negative일때 예측값을 Positive로 잘못 예측한 비율을 의미합니다.

ROC 곡선이 RANDOM CLASSIFIER에 가까울수록 모델의 분류 성능 능력이 훌륭하다는 의미입니다.

AUC 곡선은 ROC곡선 아래의 넓이를 의미하고, 최소값은 0.5, 최대값은 1입니다.
만약 넓이가 0.5라면, 모델의 분류능력이 없다고 생각하시면 됩니다.(FPR = TPR를 의미)
이는, 직선의 이름처럼 무작위로 분리하는 능력이라고 생각하시면 됩니다.

FPR을 0으로 설정하려면 임계값을 1로 설정해야합니다.
FP = 0으로 만들면 Negative로 예측 할 가능성이 매우 낮아지기 때문입니다.

FPR을 1로 설정하려면 임계값을 0으로 설정합니다.
TN = 0으로 만들면 Positive로 예측 할 가능성이 매우 낮아집니다.

FPR은 FPR = FP / (TN + FP) = 1 - TNR로 공식화 됩니다.

아래 식은 FPR = 1 - TNR이 어떻게 유도되는지에 대한 유도과정입니다.

TNR은 특이성(Specificity)로 실제값이 Negative일때 예측값도 Negative로 정확히 예측한 비율을 의미합니다.
TNR은 TNR = TN / (TN + FP)로 공식화 됩니다.

여기서 민감도, 특이성, FPR, 임계값의 서로 관계를 잘 이해해야 합니다.

민감도와 특이성은 서로 반비례 관계를 가지고 있습니다.
그러면 민감도가 증가하면 FPR은 증가하게 됩니다.
왜냐하면 FPR = 1 - 특이성으로 민감도가 증가하면 특이성은 감소하므로 FPR은 증가하게 됩니다.

그렇다면 이것을 임계값을 적용해서 그래프로 나타낼 수 있습니다.
(여기서 그림 가져왔습니다.)

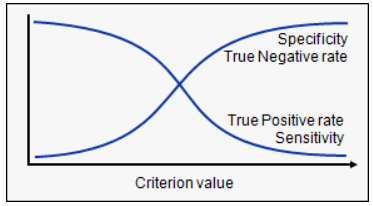
임계값을 줄인다면, 데이터의 Positive rate가 올라가게되므로 민감도는 커지고 특이성은 작아집니다.
만약 임계값이 커진다면, 데이터의 Negative rate가 올라가게되므로 민감도는 작아지고 특이성은 커지게 됩니다.

아래 코드는 FRP과 TPR에 따른 ROC 그래프의 변화를 나타낸 코드입니다.

from sklearn.metrics import roc_curve # ROC,AUC 

lr_clf.fit(train_data, train_label)
pred_proba = lr_clf.predict_proba(target_data)[:, 1] # 예측 확률 반환

fprs, tprs, thresholds = roc_curve(target_label, pred_proba)

thr_index = np.arange(1, thresholds.shape[0], 5) # thresholds[0]에는 mat(예측확률) + 1의 값이 들어 있다. 그래서 1부터 시작

print('임계값 배열 index로 추출한 임계값들\n',thresholds[thr_index])
print('FPR\n', fprs[thr_index])
print('TPR\n', tprs[thr_index])

def roc_picture(target_label, pred_proba):
  fprs, tprs, thresholds = roc_curve(target_label, pred_proba)
  
  plt.plot(fprs, tprs, label = 'ROC')
  plt.plot([0, 1], [0, 1], linestyle = '--', label = 'RANDON CLASSIFIER')

  start,end = plt.xlim()
  plt.xticks(np.round(np.arange(start, end, 0.1), 2))
  plt.xlim(0, 1)
  plt.ylim(0, 1)

  plt.xlabel('FPR')
  plt.ylabel('TPR')
  plt.show()


roc_picture(target_label, pred_proba)