디지털 영상 기초
영상 획득
세상에 존재하는 피사체를 일정한 간격으로 Sampling하고 명암을 일정한 간격으로 Quantization하는 과정을 통해 영상을 획득합니다.
Sampling : 영상을 M(가로) x N(세로)로 나눕니다. 2차원 배열이라고 생각하면 편합니다.
Quantization : 화소(Pixel)의 명암을 L개의 구간으로 나눕니다. 즉, Sampling한 배열의 element값의 범위를 정해주는것이라고 생각하면 됩니다. 예를들면 3개의 Channel을 가지고 있는 RGB이미지는 0 ~ 255까지의 각 화소값을 가지고 있습니다. 여기서 0 ~ 255는 Quantization한 범위입니다.
Resolution : 영상의 크기입니다. 흔히 해상도라고 표현하며 화소의 개수를 말합니다. 제 노트북의 해상도는 1920 x 1080이네요.
영상 좌표계
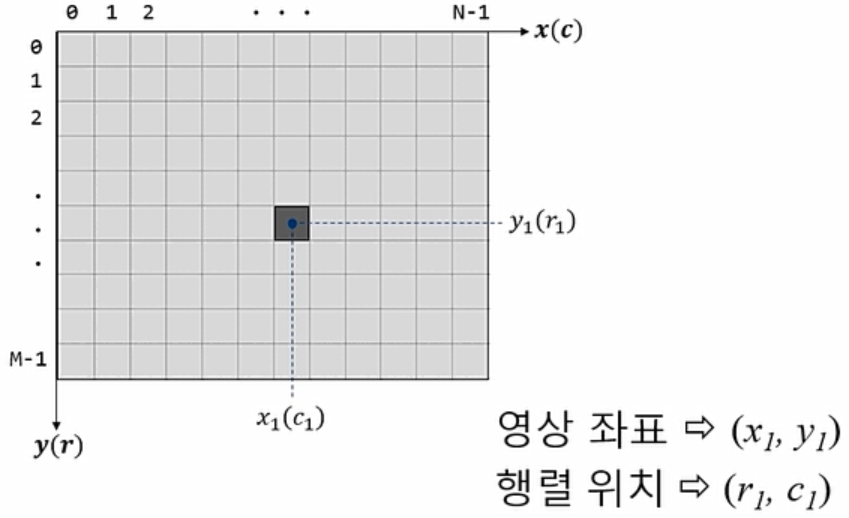
영상의 좌표는 일반적인 표기와는 다릅니다.
위의 영상 좌표계는 Gray Scale(MxN)을 예시로 든 것이고, RGB Scale(MxNxC)은 3개의 좌표축을 사용합니다. 그러면 Channel을 지정하는 C가 추가됩니다.
- 원점이 왼쪽 위 라는 점이 특징입니다.
- 화소의 위치를 지정할때는 (y,x)표기를 하지만, 그 외에는 (x,y)로 사용합니다. 예를들면 영상에 선분을 그을때는 (x,y)의 좌표를 씁니다.(영상의 위치를 지정하는 것이 아니고 선분을 지정하기 때문입니다.)
HSV
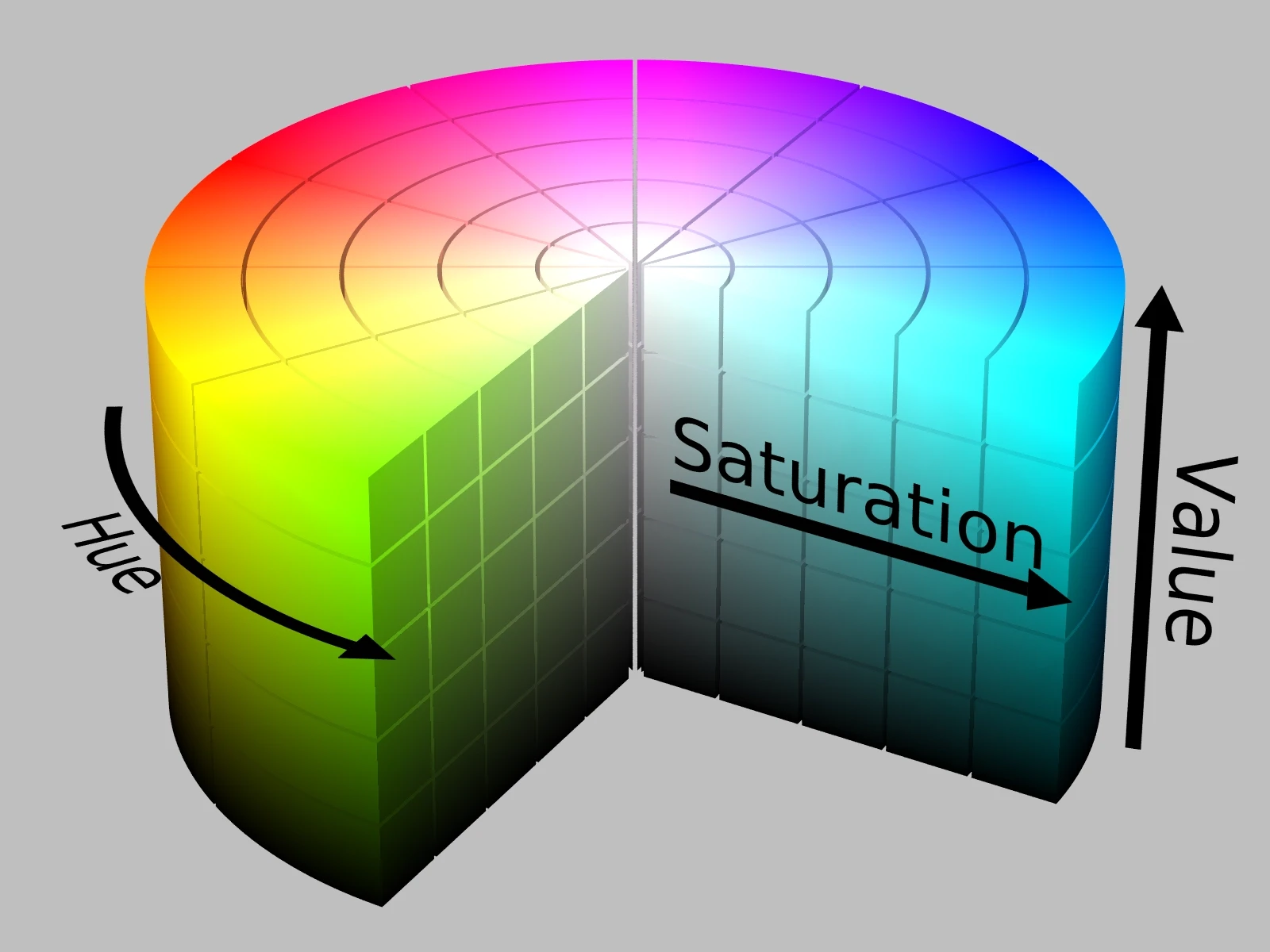
- H(Hue) : 색상
- S(Saturation) : 채도, 색의 진하고 연함 정도를 나타내는 선명도
- V(Value) : 밝기, 밝고 어두운 정도를 나타냅니다.
이진 영상
이진영상은 화소가 0(흑) 또는 1(백)인 영상입니다. 즉, 검은색과 흰색 두 가지 값만을 갖는 흑백 영상의 특별한 형태입니다.
이진화
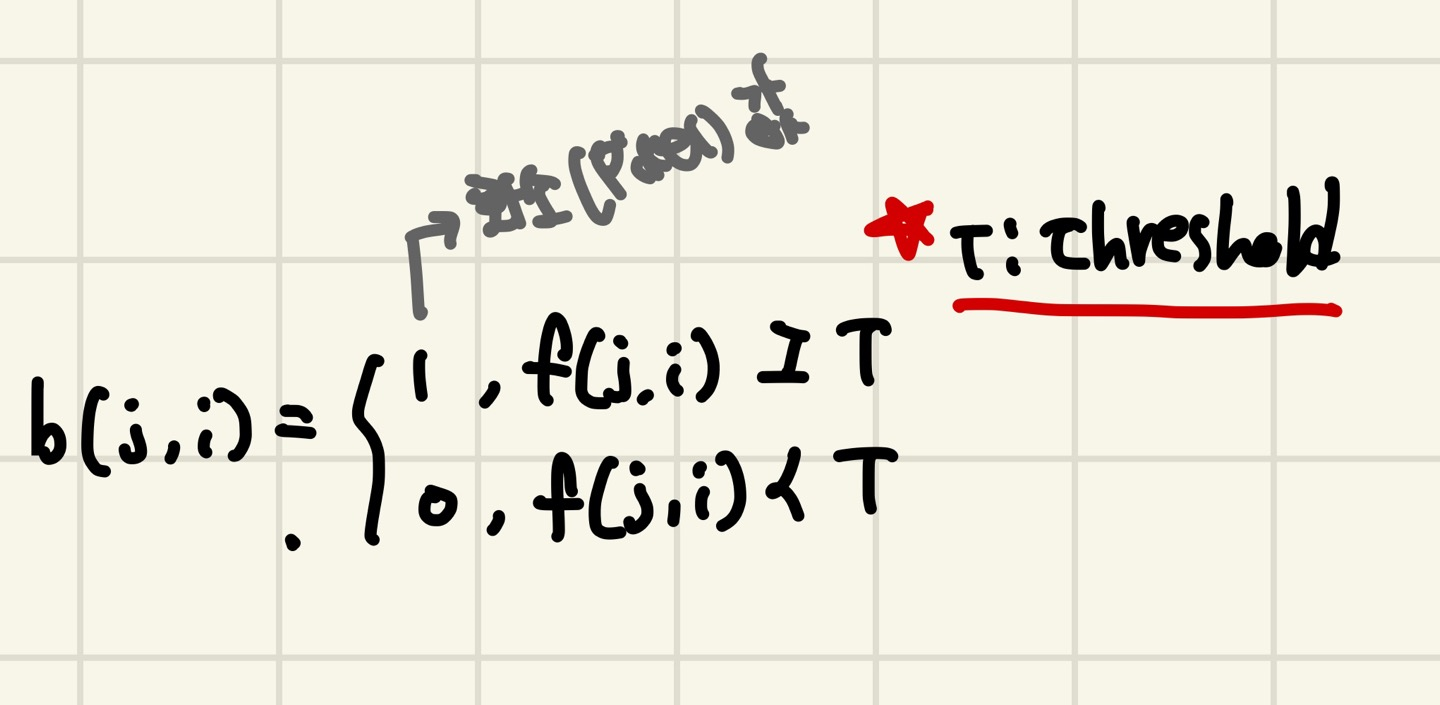영상을 이진화 하기 위해서는 임계값(Threshold)값을 정하고, 임계값을 넘으면 1(백), 넘지 않으면 0(흑)으로 값을 할당합니다.
임계값을 결정하기 위해서는 Histogram의 계곡 근처를 임계값으로 설정한다. 계곡이란, 빈도가 상대적으로 낮아지는 곳을 의미한다. 봉우리 사이라고 생각하면 편하다.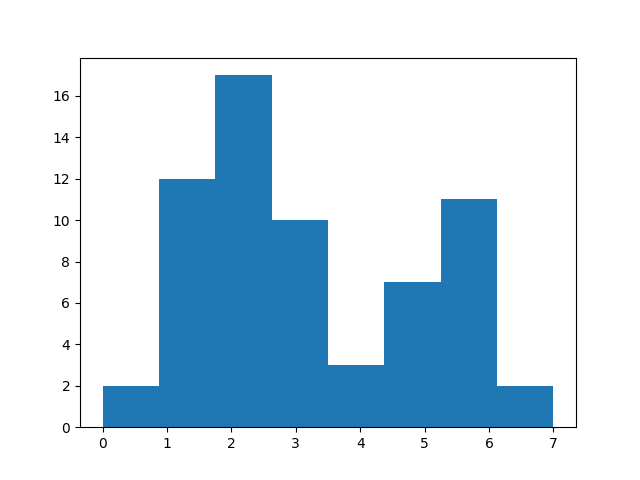
봉우리는 [0,4]와 [5,7]에서 생성이 되므로, 4에서 계곡값이 형성된다.
하지만 화소값이 더 크다면 임계값이 매우 많을 수 있기 때문에 이진화를 최적화 문제로 취급해야한다. 그래서 오츄 알고리즘으로 한개의 임계값을 정하게 됩니다.
오츄 알고리즘
계곡값이 매우 많을때 이진화를 최적화 하기 위해 최적의 임계값 구하는 알고리즘 입니다.
오츄 알고리즘의 핵심은 수많은 계곡값들중 1개의 계곡값을 정해야합니다.
즉, 임의의 임계값 T를 기준으로 화소를 두 집합으로 나누었을때, 각 집합의 명암 분포가 균일할수록 좋다는 점에 착안하여 균일성이 클수록 T에게 높은 점수를 줍니다.
명암분포가 균일할수록 흑색과 흰색의 분리가 뚜렷해집니다. 이는 높은 분류 능력을 가지는 임계값을 찾을 수 있습니다.
균일성은 분산(Variance)로 측정합니다. 분산 값이 낮을수록 균일성이 높고, 클수록 균일성이 낮습니다. 따라서 가능한 모든 T에 값을 계산하고 가장 좋은 T의 값을 임계값으로 정하는 알고리즘입니다.
연결 요소
연결 요소는 화소의 연결성을 설명합니다. 이때 이진연상에서 1의 값을 가진 연결된 화소의 집합을 연결 요소(Connected Component)라고 합니다.
(여기서는 명암 영상이 아닌, 이진영상을 기반으로 작성합니다.)
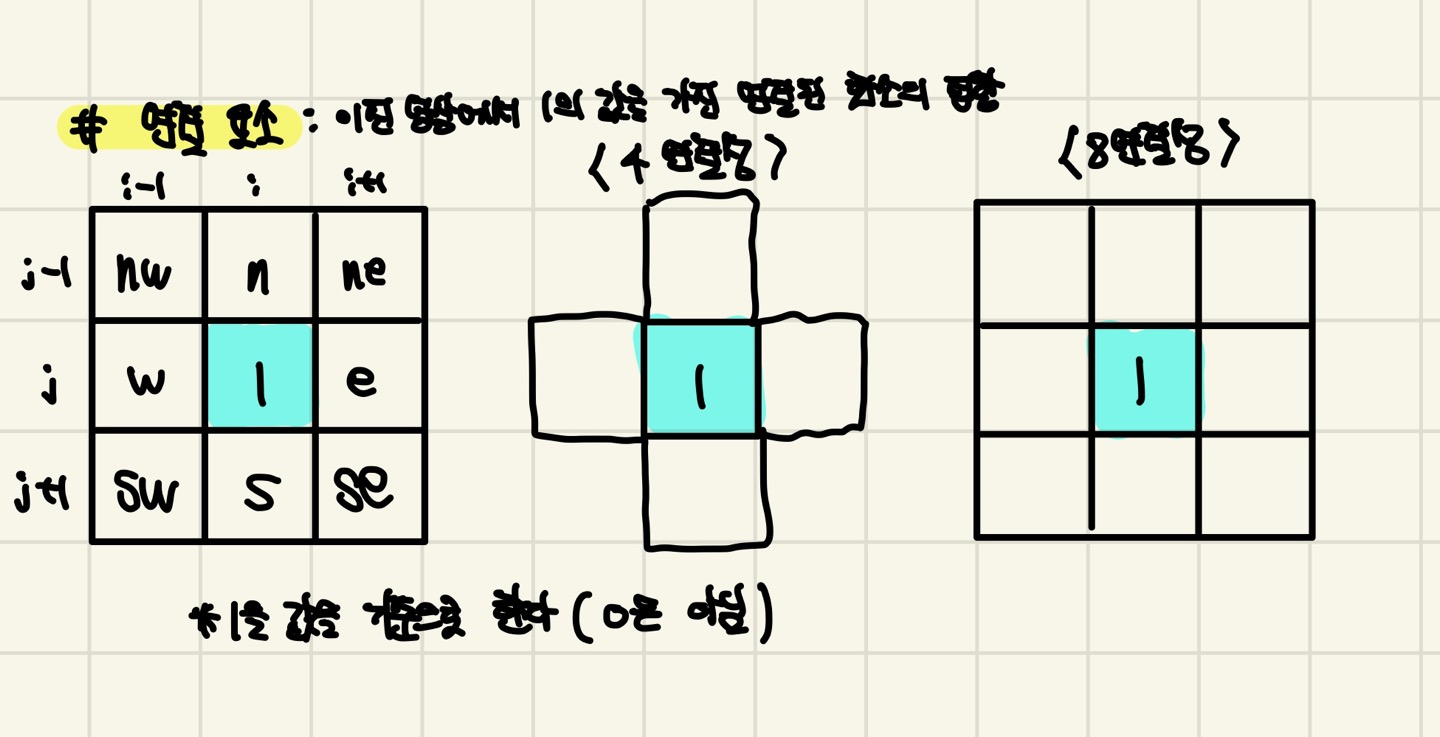
모폴리지
모폴리지(Morphology)는 영상 내에 객체의 형태와 구조를 조작하고 개선하는데 사용합니다. 모폴리지는 구조 연산(Structure Element)에 따라서 영상의 결과가 달라집니다.
모폴리지의 기본연산은 팽창(Dilation)과 침식(Erosion)이 있습니다.
(여기서는 명암 영상이 아닌, 이진영상을 기반으로 작성합니다.)
- 팽창 : 영상에서 작은 홈을 메꾸거나, 끊어진 영역을 하나로 연결할때 사용합니다. 구조요소의 중심을 1인 화소에 씌운 다음 구조 요소에 해당되는 모든 화소를 1로 바꿉니다.
- 침식 : 영상에서 영역의 경계에 돌출 부분을 깍아낼때 사용합니다. 구조 요소의 중심을 1인 화소에 씌운 다음 구조 요소에 해당하는 모든 화소가 1인 경우에 구조 요소의 중심화소를 1로 유지, 그렇지 않으면 0으로 값을 바꾸어줍니다.
- 열림 : 침식에서 팽창으로 변환
- 닫힘 : 팽창에서 침식으로 변환
점 연산
점 연산, 영역 연산, 기하 연산에 들어가기에 앞서 영상처리에서 연산은 화소가 새로운 화소값을 받는 과정이라고 생각하면 됩니다.
점 연산은 자기자신으로부터 값을 받고, 영역 연산은 이웃 화소의 값을 보고 값을 결정, 기하 연산은 기하학적 변환에 따라 다른곳으로부터 값을 받습니다.
명암 조절
f'은 새로운 화소의 값입니다.
a는 원래 영상의 화소 값을 의미합니다.
밝게 하기위한 식을 보면 min은 화소의 값의 지정된 max값에 벗어나지 않기 위해 min값으로 구하고, 어둡게 하기위한 식을 보면 max는 화소의 음수값을 방지하기 위해 max값으로 구합니다.
변수들간의 관계를 직선으로 나타낼 수 있어서 선형연산으로 말합니다.
하지만, 우리 인간들의 눈은 영상의 명암을 조절하게 되면 그 명암값을 그대로 받아들이지 않고 비선형적으로 값을 받습니다. 즉, 실제 영상의 화소값을 변경하면 변경된 화소값만큼 눈은 받아들이지 않습니다.
f'r은 [0,1]로 기존의 화소값을 정규화 한 값입니다.
r = 1이면 원래 영상, r > 1이면 기존 대비 어두운 값, r < 1이면 기존 대비 밝은 값을 받습니다.
히스토그램 평활화
히스토그램 평활화(Histogram Equalization)는 히스토그램이 평평하게 되도록 영상을 조작해 영상의 명암 대비를 높이는 기법으로 영상에 있는 물체를 더 잘 식별할 수 있도록 합니다.
픽셀이 어두운쪽이나 밝은쪽에 몰려있으면 사진이 너무 밝거나 어둡습니다. 그래서 히스토그램 평활화를 하면 대비가 더 강해지기 때문에 물체가 더 잘 식별 됩니다.
즉, 명암대비가 뚜렷하지 않은 영상의 명암대비를 뚜렷하게 만들어준다고 생각하시면 됩니다.
이때 명암의 빈도는 같습니다.
명암의 빈도가 같기 때문에 사진에 노이즈가 발생할 가능성이있습니다.
위의 사진으로 평활화 한 이미지에서 노이즈가 증가하는 이유를 알 수 있습니다.
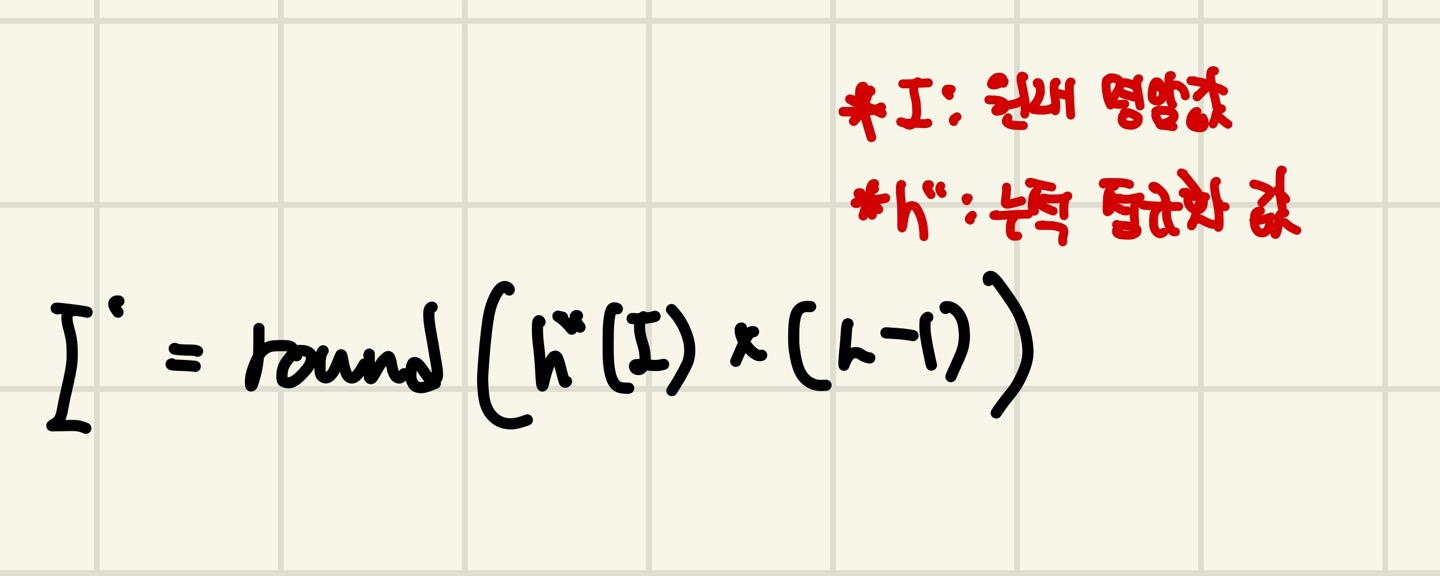
위의 식은 히스토그램 평활화를 위한 식입니다. round는 반올림을 뜻합니다.
어두운 값은 더 어둡게 밝은 값은 더 밝게 합니다.(명암 대비를 높여주기 위해)
영역 연산
컨볼루션
컨볼루션(Convolution)은 신경망에서 활용하는 진짜 매우 중요한 연산입니다.
컨볼루션은 입력 영상 f 각 화소의 필터를 적용해서 곱의 합을 구하는 연산입니다. 필터는 영상을 변환하는 의도에 따라서 필터의 종류(값)이 바뀌게 됩니다.
위의 식은 컨볼루션을 적용하는 식입니다.
2차원 필터는 크기를 h x w로 표시하고 대칭성을 위해서 홀수로 지정합니다.
영상의 이미지의 가장자리부분은 컨볼루션이 불가능합니다. 그렇기 때문에 덧대기(Padding)으로 컨볼루션을 연산합니다.
- Zero Padding : 필요한 만큼 가장자리를 확장 하고 확장한 부분을 0으로 채웁니다.
- Copy Padding : 필요한 만큼 가장자리를 확장하고 확장한 부분을 영상의 가장자리 값으로 채웁니다.
위 사진은 Copy Padding의 예시입니다. Zero Padding은 Copy Padding의 확장한 부분에 0으로 채워주게 되면 Zero Padding이 됩니다.
블러링
아래의 내용은 개인적인 생각으로 컨볼루션 다음 중요한 개념입니다.(특히 가우시안 필터)
블러링(Blurring)은 영상을 부드럽게 만듭니다. 즉, 영상의 잡음의 영향을 제거하는 전처리 과정에서 사용되는데 노이즈를 제거한다고 생각하시면 됩니다.
블러링안의 평균값 필터(Mean Filter)와 가우시안 필터(Gaussian Filter) 등이 있습니다.(원래 더 많은데 여기서 2가지에 대해 설명합니다.)
평균값 필터
평균값 필터는 영상에서 특정 화소와 주변 화소들의 평균을 결과 영상 화소값으로 설정합니다. 이 필터를 적용하면 화소값의 급격한 변화가 줄어들기 때문에 날카로운 에지가 무뎌지고 잡음의 영향이 크게 감소합니다.
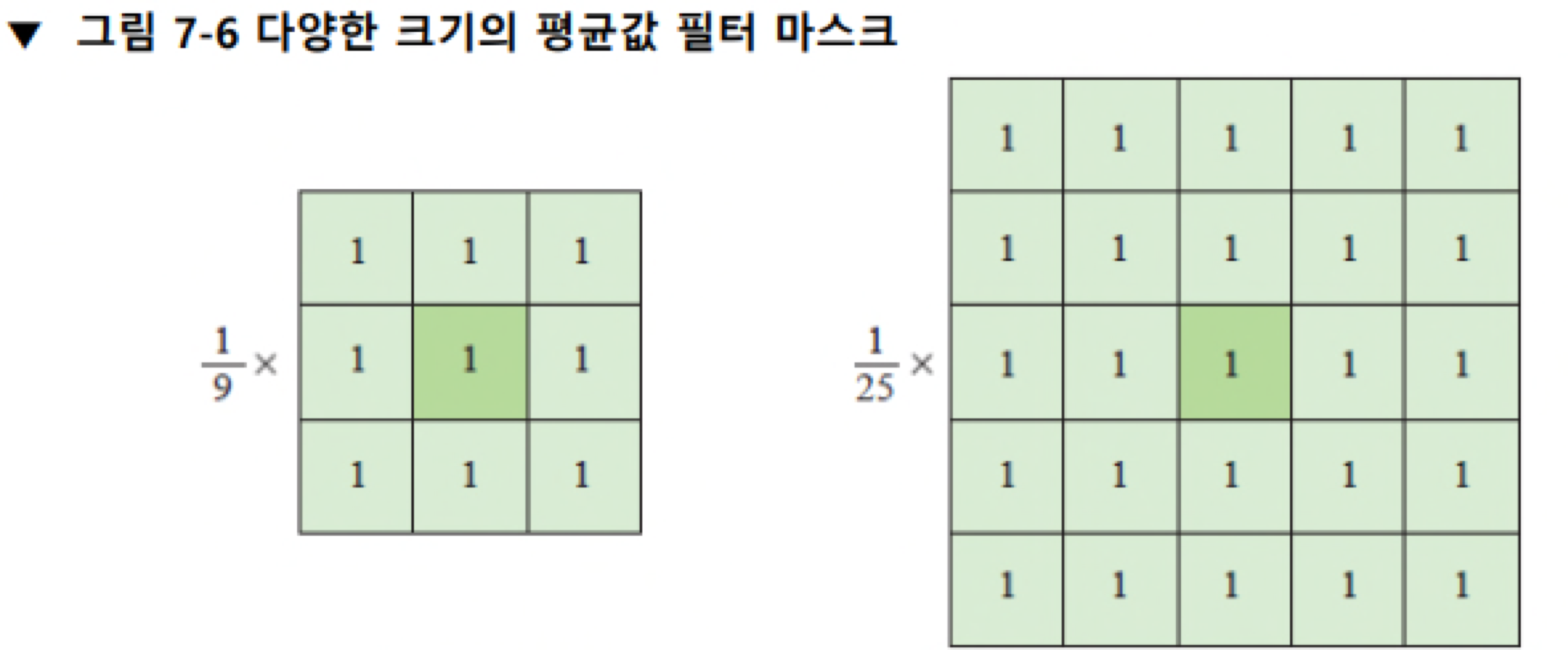
평균값 필터의 크기가 커질수록 더욱 부드러운 느낌의 결과 영상을 생성하지만, 연산량이 크게 증가한다는 단점이 존재합니다.
필터의 앞의 분수값은 화소의 element들의 개수에 비례해서 분모값이 결정됩니다.
주변 픽셀들의 평균값을 결정하기 때문입니다.
가우시안 필터
가우시안 분포(Gaussian Distribution)함수를 근사하여 생성한 필터링 기법입니다. 평균값 필터보다 자연스러운 블러링 효과를 보여줍니다.
가우시안 분포는 정규 분포와 같은 말입니다.
평균을 중심으로 좌우 대칭인 확률 분포이며 종 모양을 갖습니다. 평균 근방에서 분포가 가장 많이 발생하고 평균에서 멀어질수록 발생 빈도가 줄어들기 때문에 종 모양으로 감소하는 형태를 이룹니다.
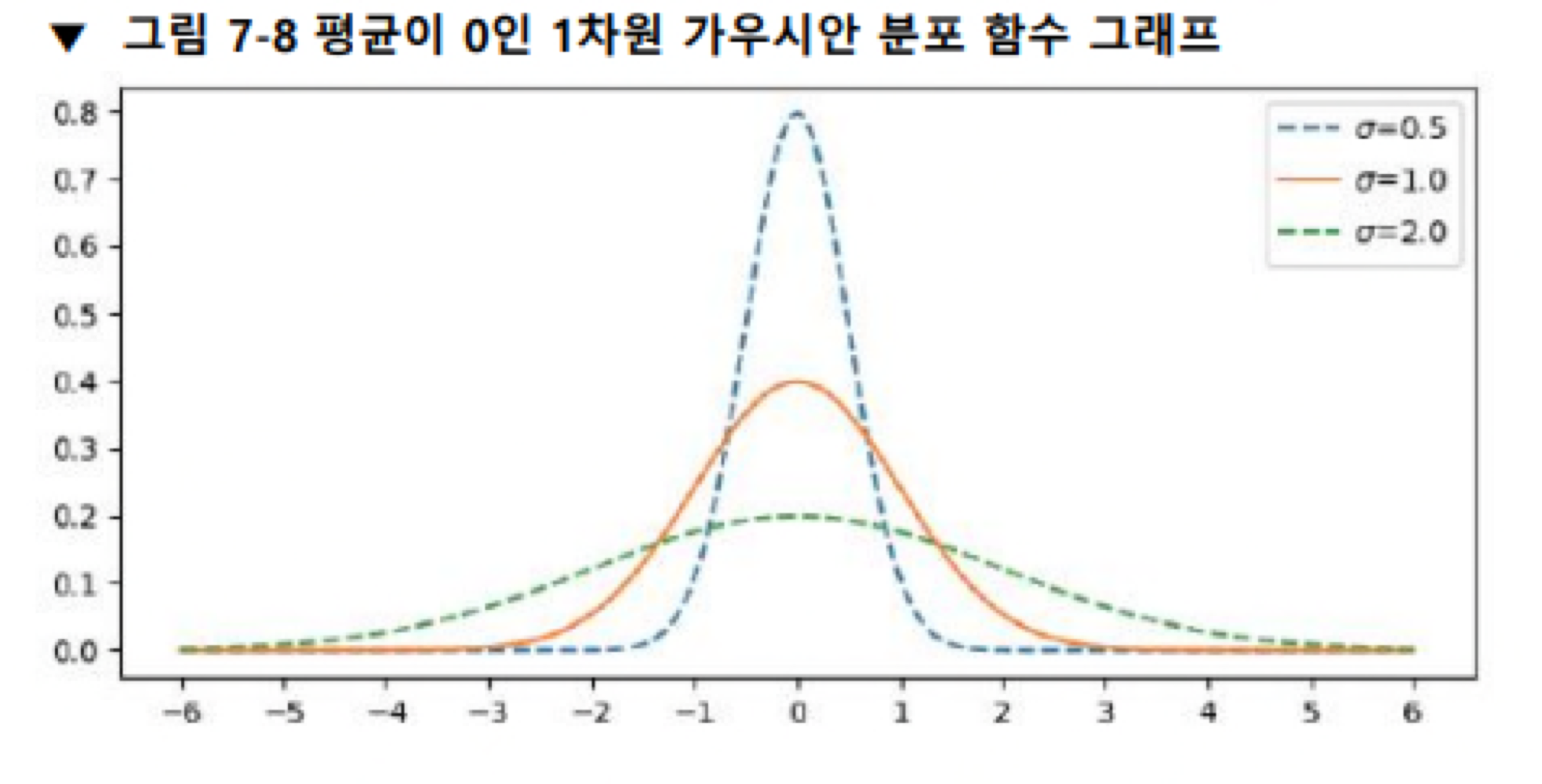
위 사진은 표준편차에 따라서 가우시안 그래프는 평균과 표준편차에 의해 그래프가 바뀌는 것을 볼 수 있습니다.
표준편차의 값이 크면 봉우리가 낮아지고 멀리까지 퍼지며 작으면 봉우리가 높아집니다.
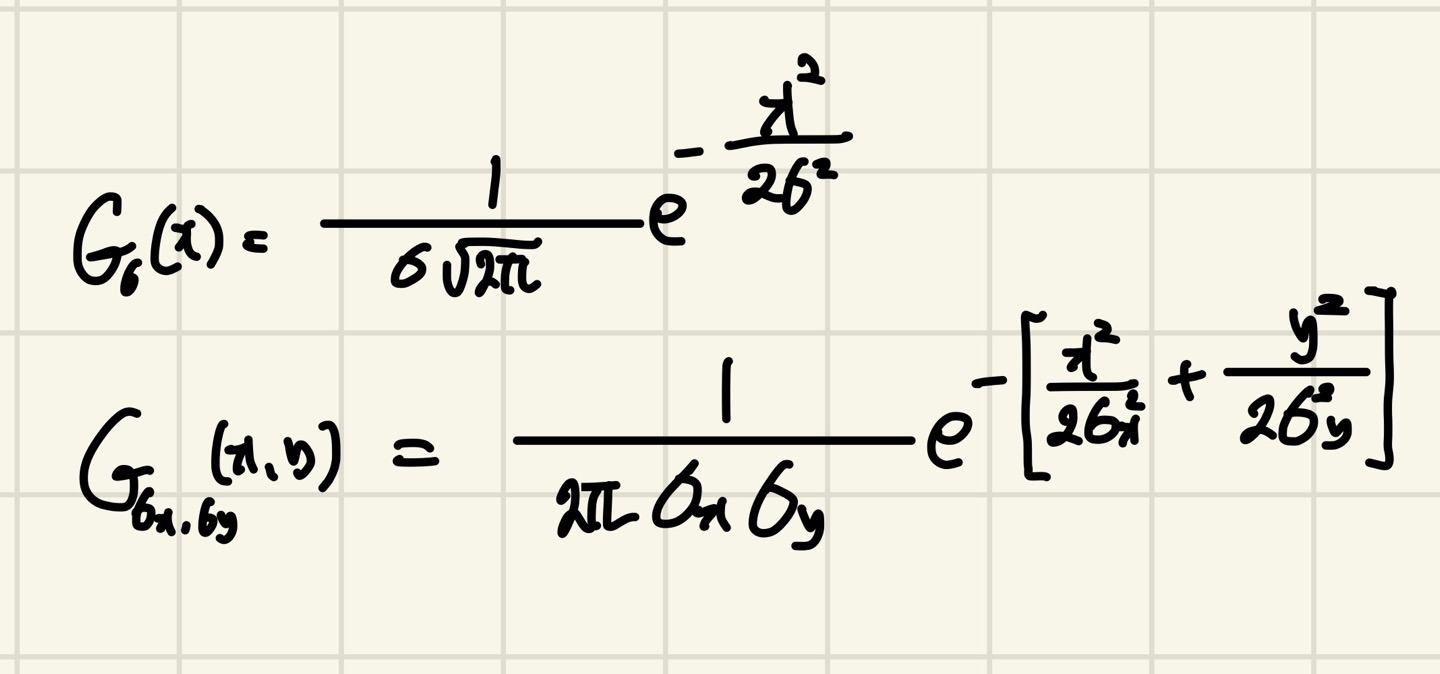
위 사진은 종속변수의 개수에 따른 가우시안 함수 식입니다.
종속변수가 1변수이면 위, 2변수이면 아래의 식을 쓰면 됩니다.
원래 각 x,y에서 평균값을 빼주어야하는데 영상에서 평균값은 0을 주로 사용하기 때문에 값을 빼고 식을 썼습니다.
x,y는 필터의 중심에서의 상대적인 좌표를 나타냅니다.
x : 중심에서부터 열 방향의 거리
y : 중심에서부터 행 방향의 거리
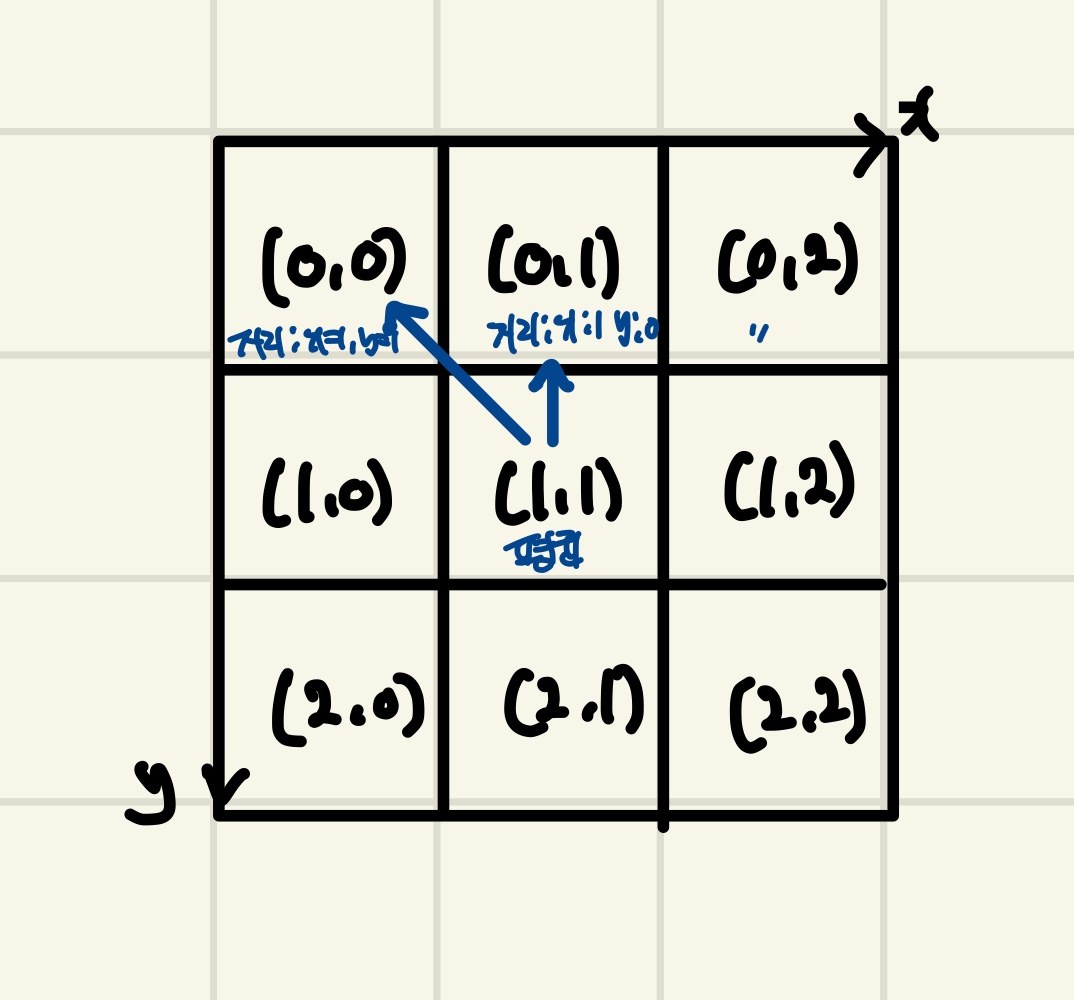
제가 처음에 x,y의 값이 뜻하는 정의가 뭔지 몰라서 저처럼 이해가 되시지 않는 분들을 위해서 따로 그림으로 표현해봤습니다.
위 사진은 가우시안 함수를 적용해서 필터를 생성한 가우시안 필터입니다. 중심화소의 값이 가장 크고 중심화소의 값에서 멀어질수록 값이 작아지는것을 볼 수 있습니다.
조금 더 자세히 말하면 필터링 대상 화소 근처에는 가중치를 크게 주고, 필터링 대상 화소와 크게 떨어져 있는 주변부에는 가중치를 조금만 주어서 가중 평균을 하는 것과 같습니다. 가중치는 거리를 뜻합니다.
(가중평균이란 각 값에 다른 가중치를 적용하여 계산하는것을 말합니다.)
기하 연산
기하연산은 영상의 크기를 조절하거나 영상을 회전하기 위한 연산입니다.
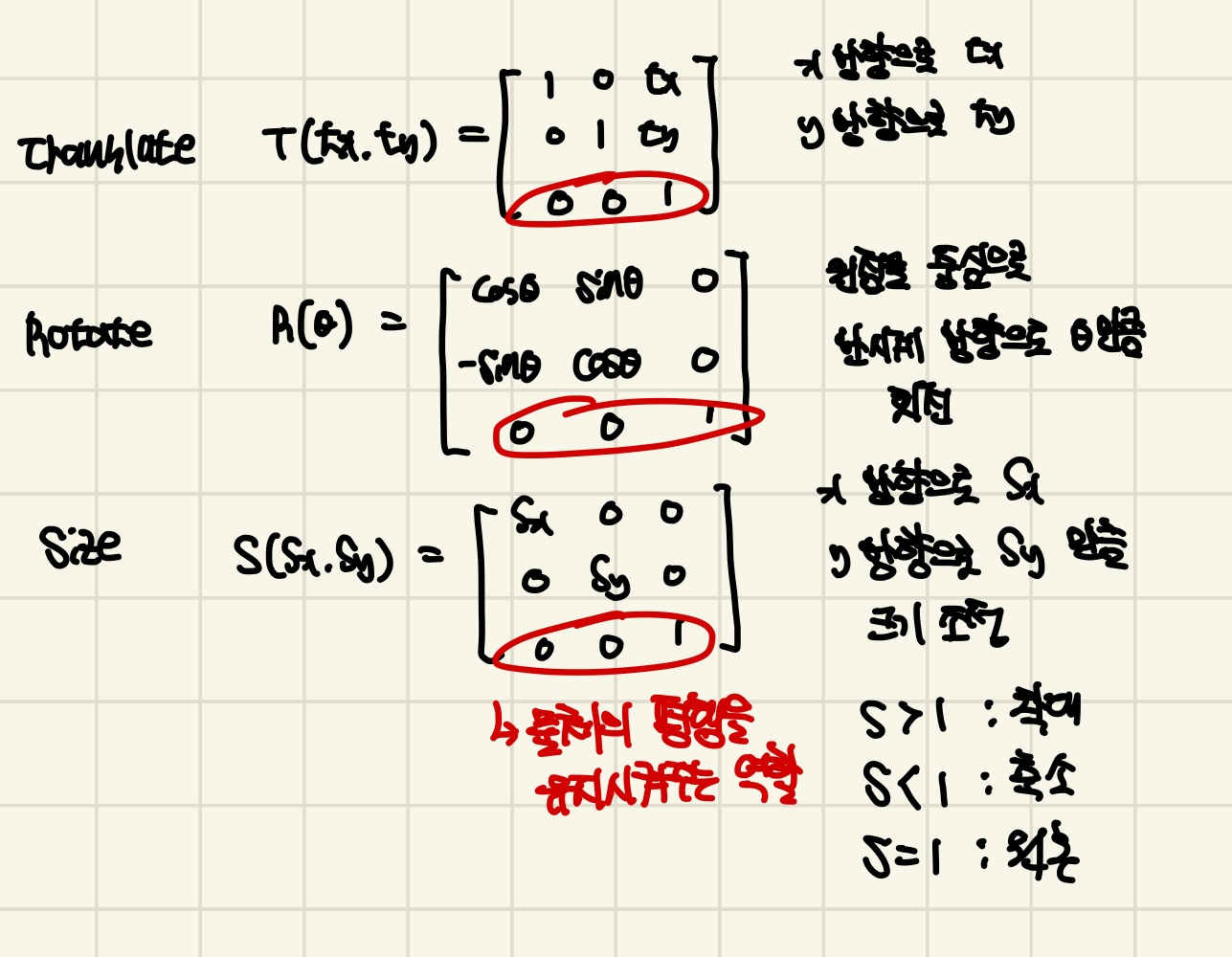
위 사진은 이동(Translate), 회전(Rotate), 크기(Size)를 수행하는 행렬들을 나타낸다.
이동,회전,크기를 수행해도 물체의 상태는 그대로 유지가 되기 때문에 Affine 변환이라고 한다. 그리고 각 행렬들은 Affine Matrix라고도 불리운다.
Affine 변환과 반대되는 개념은 Projective 변환으로 물체의 상태가 변환된다.
조금 더 깊게 들어가서, 만약 영상을 회전을 주었다고 하자. 만약 회전한 물체의 위치가 정수값이 아닌 실수값이면 문제가 생기게 된다.(화소의 위치는 실수값이 아닌 정수값으로 지정합니다.)
예를들면, (1,3)의 위치에 있는 물체를 회전시켰더니 (3.12, 0.18)로 변환 되었으면 안된다라는 뜻이다.
만약 실수 좌표를 반올림한다면 특정 위치에는 화소값을 받지 못하기 때문에 Aliasing이 일어날 수 있다. Aliasing은 시각적으로 불만스러운 현상을 말합니다.
Aliasing을 누그러뜨리는 Anti-Aliasing이 있는데 입력 영상의 어파인 행렬을 적용한 결과물에서 결과 영상에 어파인 행렬의 역행렬을 적용하면 원래 영상의 해당 화소를 찾습니다.
하지만 여전히 화소의 위치가 실수일 수 있기 때문에 실수 좌표를 정수로 변환하는 작업이 필요합니다.
그렇기 때문에, 역행렬보다는 영상 보간(Image Interpolation)을 활용해야한다.
보간은 Aliasing이 난 화소의 위치에 값을 할당하는 방법입니다.
- 최근접 이웃(Nearest Neighbor) : 반올림을 사용해 가장 가까운 화소에 배정하는 기법
- 양선형 보간법(Bilinear) : 4개의 화소와 걸친 비율에 따라서 가중 평균하여 화소값을 계산합니다.
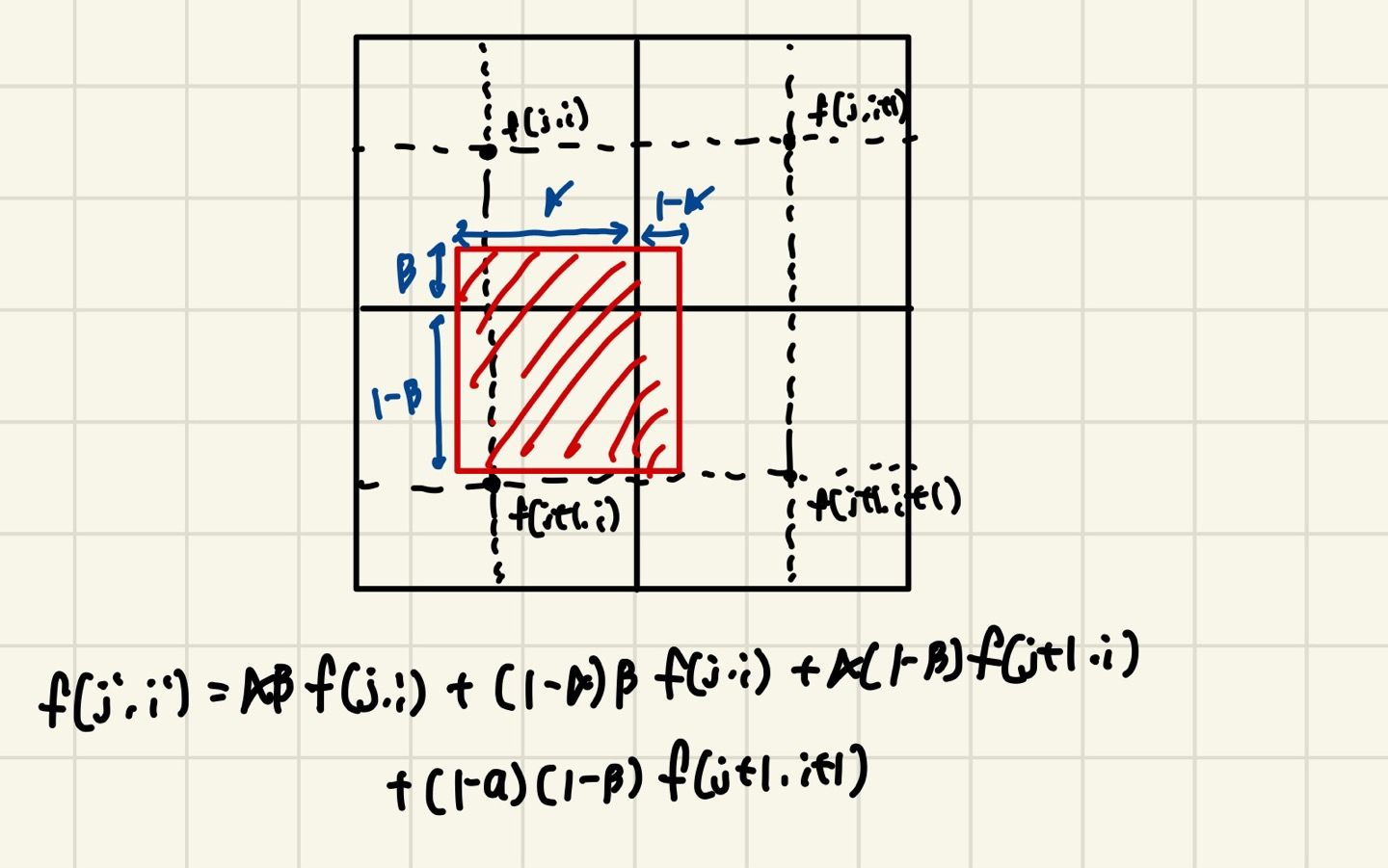
위 사진은 주변 4개의 화소값과 α,β값의 가중평균으로 화솟값을 결정합니다.
- 양 3차 보간법(Bicubic) 16개의 이웃과 3차 함수를 사용하여 보간
- 선형 보간법(Linear) : 1차원 직선 상에 두 점이 주어졌을때, 그 사이의 값을 추정하기 위해 직선 거리에 따라 선형적으로 계산
영상처리는 컴퓨터비전에 굉장히 중요한 학문이여서 열심히 공부해야겠습니다 ㅜㅜ
혹시라도 틀린 부분이 있으면 말씀해주세요
읽어주셔서 감사합니다 :>
