영상처리1(Transformation)

Geometric Transformations

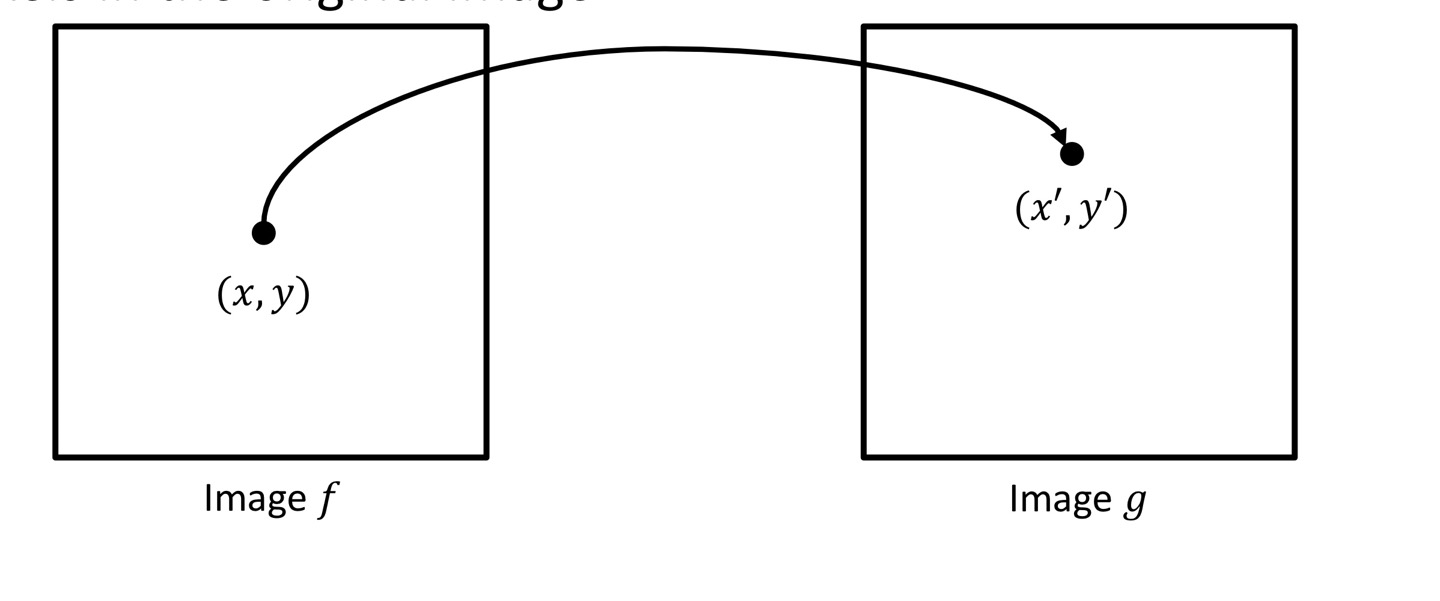
Geometric Transformation은 (x,y)에 있는 이미지 pixel의 위치가 (x',y')으로 변환되는 것을 의미합니다.

더 정확히 말하면, f(x,y)의 value가 바뀌는 것이 아니고 x와y의 값이 바뀌어서 pixel의 위치가 변환된다고 보시면 됩니다.

이러한 transformation은 (x,y)에 Affine Matrix를 곱해주면 위치가 변하게 됩니다.

Affine Matrix를 통해 Scale, Rotate, Translate을 수행할 수 있습니다.

x'은 변환된 (x,y)의 좌표이고 AX는 Transformation을 해주는 연산이라고 보시면 됩니다.

만약, 변환된 위치를 다시 원래의 위치로 돌리고 싶다면 Affine Matrix의 Inverse Matrix를 곱해주면 됩니다.
Noise가 일어난다면 다양한 Interpolation기법을 생각할 수 있는데, 다음 포스트때 다뤄보겠습니다.(영상처리 기초에 간단히 설명해놨음)

Intensity Transformation

저희는 이번에 Geometric이 아닌 Intensity Transformation을 볼겁니다.
Intensity는 pixel의 값을 변환하여 이미지의 밝기를 키울 수 있고, Noise를 제거할 수 있습니다.

이미지를 얻기 위해서는 저희는 object가 있어야합니다.
하지만, 이미지가 빛에 반사되어 상에 맺히게 되니, 빛도 필수적이겠네요.
그러면 단순히 생각해보면 빛과 반사만 있게되면 이미지를 얻을 수 있습니다.
그렇다면 f(x,y) = i(x,y) x r(x,y)라는 식으로 이미지를 얻을 수 있습니다.

이때 i는 빛에너지 크기로 0보다 크고 무한대보다 작습니다.
r은 빛의 반사도로 object의 자체의 특성으로 Constant의 값을 가지므로 0보다 크고 1보다 작은 값을 가지게 됩니다.

Pixel

• 오로지 Positive한 value값을 가집니다.
• Intensity라고 불리웁니다.
• [0, L - 1]의 range의 값을 가집니다.

우리가 해상도(Resolution)이라고 불리우는것도 Pixel의 개수를 말합니다.
만약 H x W의 이미지의 size가 있다면, HW의 Pixel개수가 있고 HW bytes의 용량이 필요로 하게 됩니다.(1Pixel당 1byte)
만약 동영상이라면 1frame이 가지는 용량이 매우크기 때문에 이미지를 압축시킬 필요가 있습니다.

이제 본격적으로 Intensity Transformation에 대해서 설명드리겠습니다.

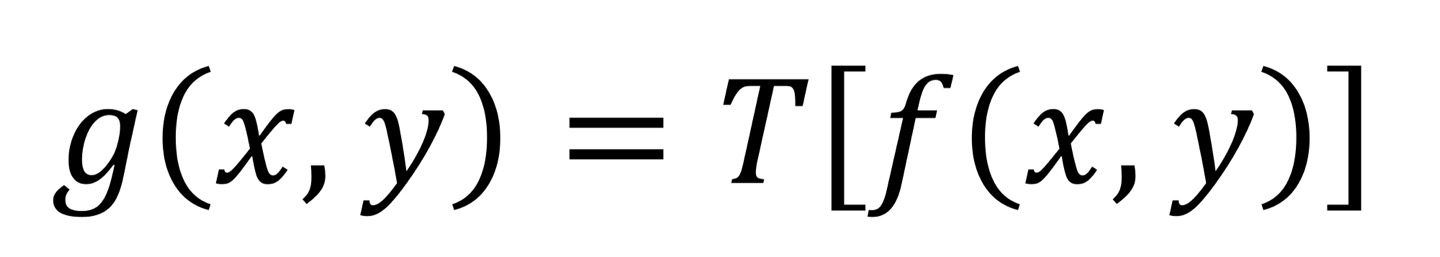
저희는 앞서 영상처리 기초 포스트에서 f(x,y)는 (x,y)의 pixel값을 가진다고 말씀드렸습니다. 즉, Intensity가 되겠네요.
그렇다면 단순히 Intensity는 값이기 때문에, (x,y)의 값은 필요가 없게 됩니다. 왜냐하면 똑같은 위치에서의 Intensity값만 바꾸기 때문입니다.

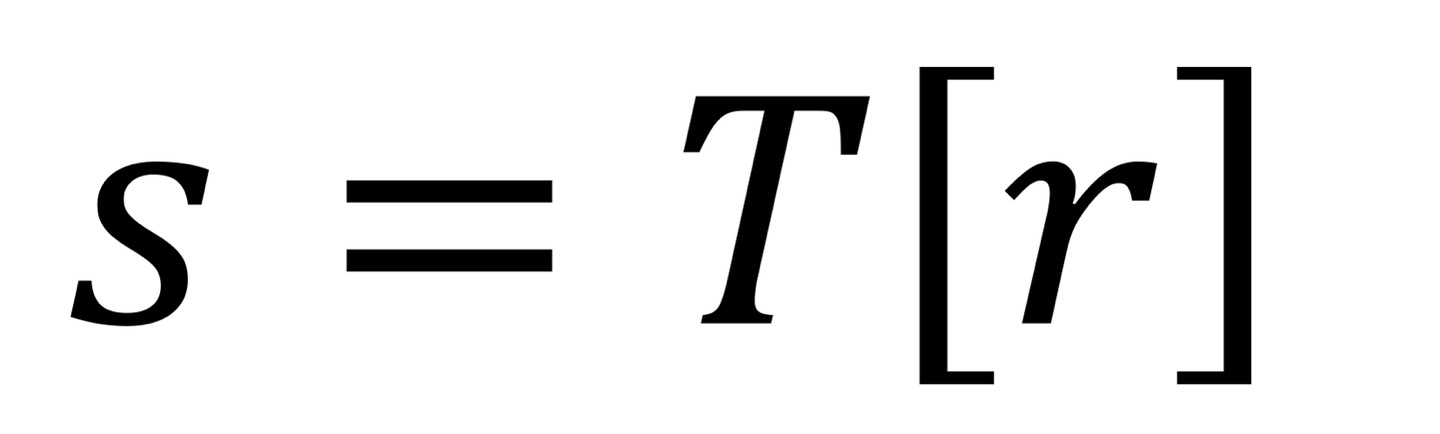
그러면 단순히 위의 식으로 바뀌게 되는것을 이해할 수 있습니다.

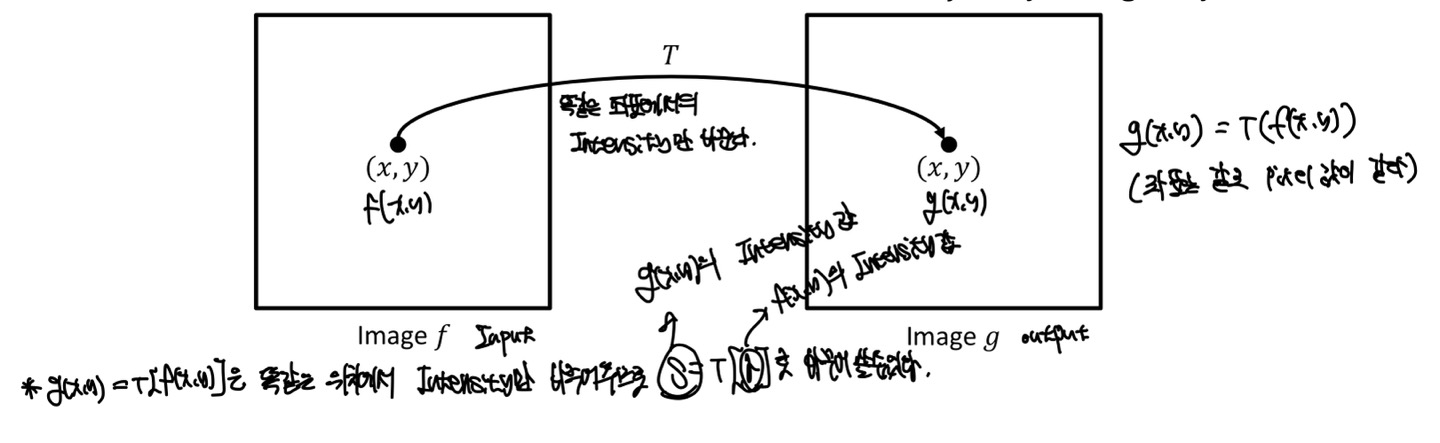
다양한 Intensity Transformation이 있지만, 가장 중요한 Gamma Correction이 있습니다.

Gamma Correction

Gamma Correction의 공식입니다.
r / L은 정규화를 한 값으로 0~1사이의 값을 가지고 있고, HyperParameter인 감마의 값을 잘 조정해야합니다.

감마의 값을 조정할 수록 다음과 같은 그래프가 나오게 됩니다.
감마가 작은 값이라면, 좁은 범위의 어두운 입력값을 더 넓은 범위의 출력값으로 매핑합니다.
1보다 큰 값을 가지면 반대의 효과가 일어나겠네요.

---

Bit-Plane Slicing

만약 어떠한 Image가 있다고 한다면, 각 Pixel(화소)의 값을 decimal로 표현하지만, 실제로 컴퓨터에서는 decimal value를 binary value로 표현할 것 입니다.

만약 Image가 8bit로 표현이되고, Image의 1개의 Pixel값이 180이라면 10110100(2)로 binary value로 채워집니다.

이때 맨앞의 숫자를 MSB(Most Significant Bit)이라고 표현하고, 맨 뒤의 숫자를 LSB(Least Significant Bit)라는 용어를 씁니다.

본론으로 돌아와서, 그렇다면 Image의 size(Resolution)가 WxH로 표현된다면, Image는 WxH만큼의 Pixel이 있게됩니다.

그렇다면, 각 binary value로 채워진 Pixel값들을 각 bit자리수마다 1개의 Image를 만들면 어떻게 될까요?
그러면 8개의 Image가 만들어지고, 각 Image는 binary값으로 영상을 만들게 됩니다.

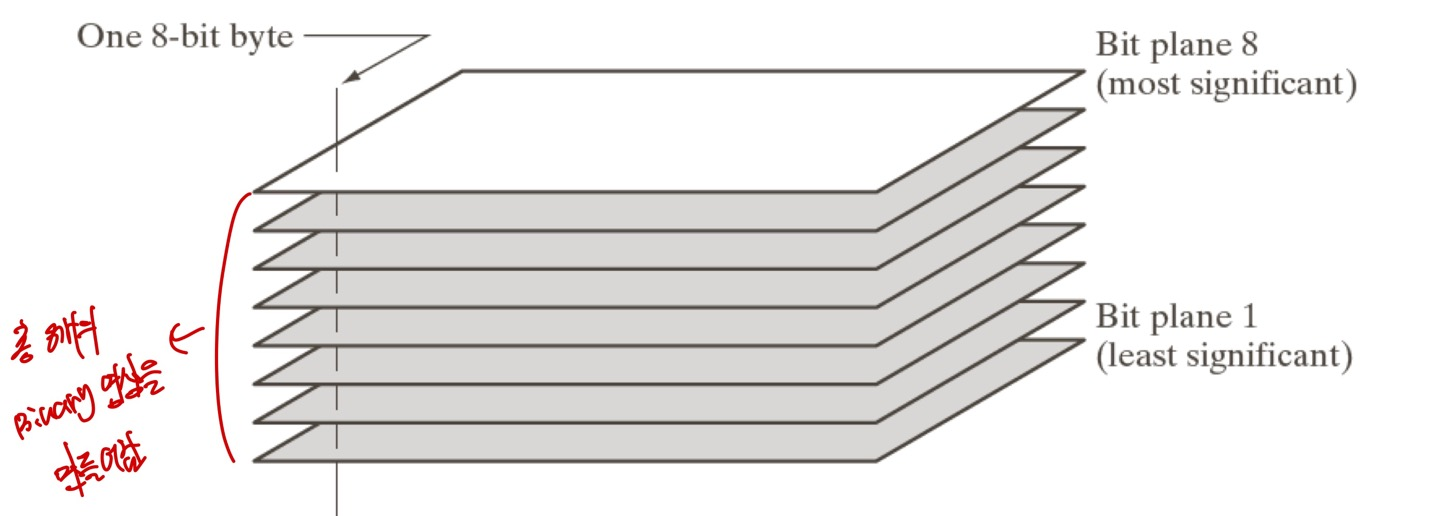
방금 말씀드린것을 위의 그림과 같이 나타낼 수 있습니다.

Image에서 각 Bit마다 Image를 만들어 낸 Image를 "Bit plane"이라고 부르고, 만약 MSB에서 Bit Plane을 만들었다고 한다면, Bit Plane8 이라고 부르게 됩니다.

그러면 각 Bit에서 표현하는 그림을 한번 보겠습니다

위의 그림을 설명드리겠습니다.
Bit8 Image를 통해 설명드리면, bit8의 value로만 이루어진 Image인 것을 알 수 있습니다.
그렇다면, 1과0으로만 이루어져있는데(0인 경우 검정색 or 어두운 색, 1인 경우 흰색 or 밝은색)이 1값은 Pixel값으로 128($2^7$)을 나타내고 0값은 0의 pixel값을 가지게 됩니다.

그러면, Bit8의 Image는 0과1에 따라서 Image를 표현하는 정보가 많겠죠? 왜냐하면 0과1에 대한 Pixel의 차이가 크니까요.

그러면 Bit8부터 Bit1까지 0과1에 대한 Pixel 차이가 줄어들면서 원래 Image에 대한 정보도 줄어들게 될 것입니다.

그래서, bit1의 이미지는 0과1의 차이가 Pixel값이 1차이로 흰색과 검정색이 나누어지기 때문에, 우리 눈에는 지지직 거리는 Image를 볼 수 있는 것 입니다.

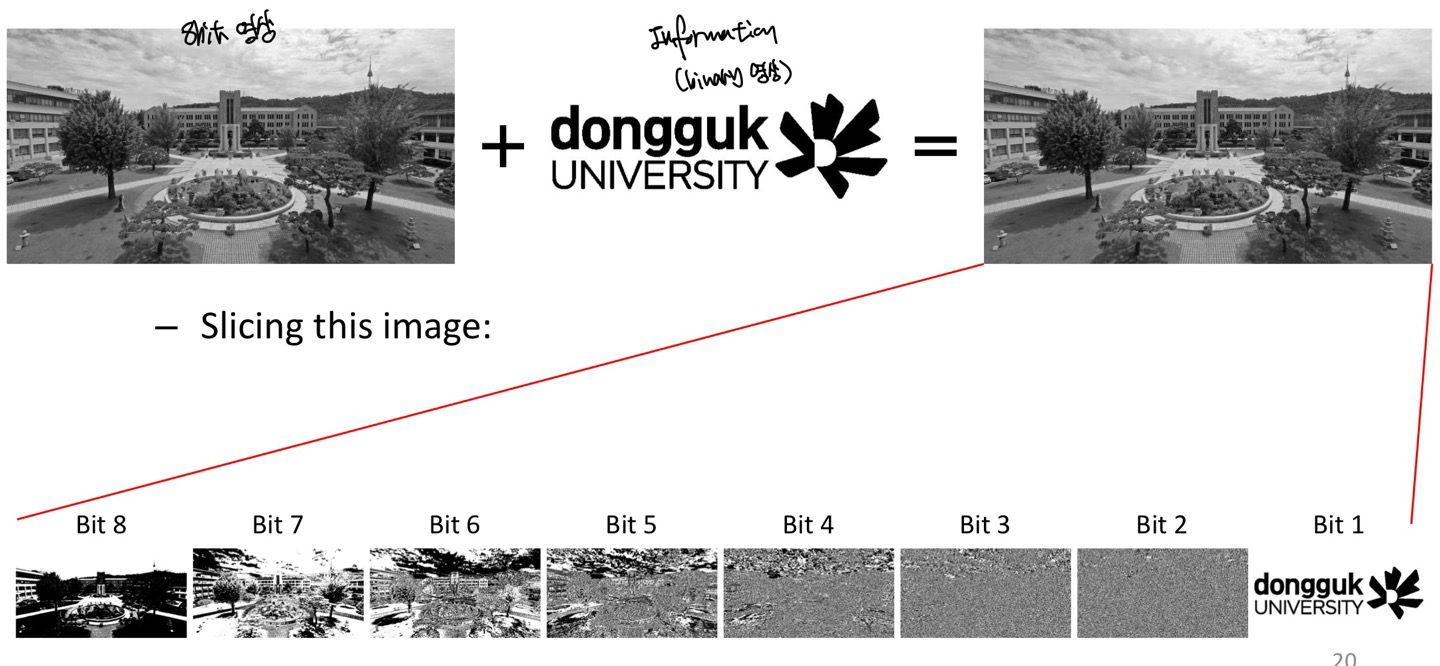
이러한 특징으로 저희는 실생활에서 WaterMarking이라는 기술을 쓰는데요.
bit1이 가지는 Image의 정보가 별로 없다보니, bit1에 중요한 Image를 숨기는 기술을 쓰고는 합니다.

위 그림은 위의 bit로 각각 나눠진 bit plane들을 합친 것을 보여줍니다. bit8-7은 bit8과 bit7을 이용한 Image라고 보시면 되겠네요. 그렇다면, bit8과 bit7을 이용하니 2개의 비트를 쓰므로 4가지의 색으로 표현한다는 것을 알 수 있습니다.(gray scale Image 입니다.)

위의 그림으로도, bit가 큰 것으로 Image를 합쳐도 Image에 대한 정보가 많기 때문에, 겉보기에 bit8-5 Image와 bit8-1 Image가 차이가 별로 없는 것을 볼 수 있습니다.

---

Histogram Equalized

우리가 중,고등학교때 배웠던 Histogram이 맞습니다.
Histogram은 어떠한 정보를 numerical data의 distribution으로 대략적인 수치를 보여줍니다.
이러한 Histogram으로 우리는 Image의 Pixel의 distribution을 알아보고 조작을 통해 Image를 시각적으로 개선시키는데 사용합니다. --> Histogram Equalized에 대해서 배웁니다!!

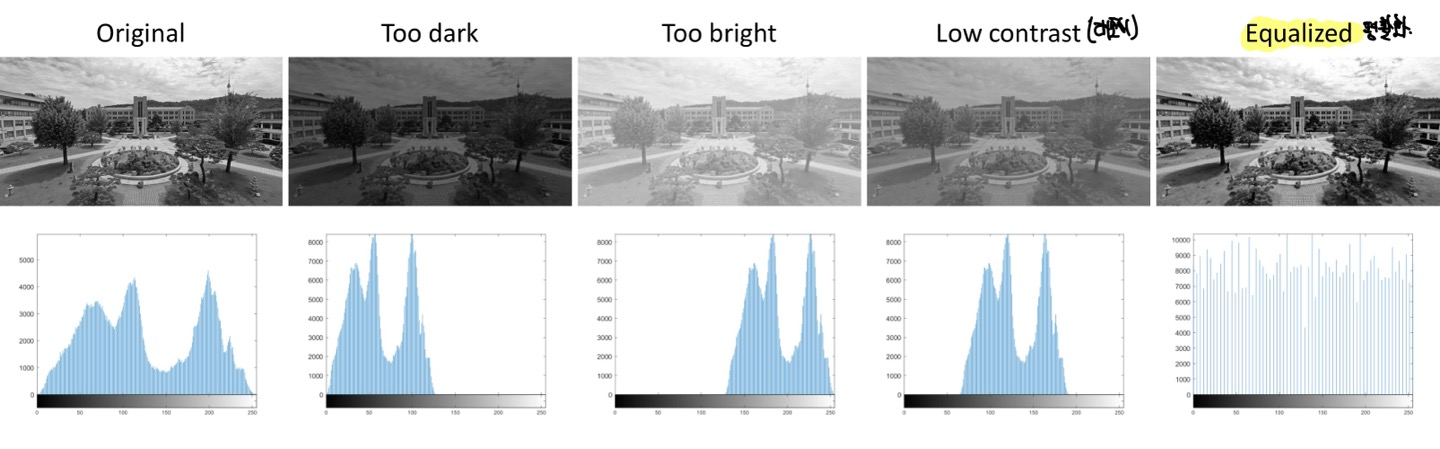
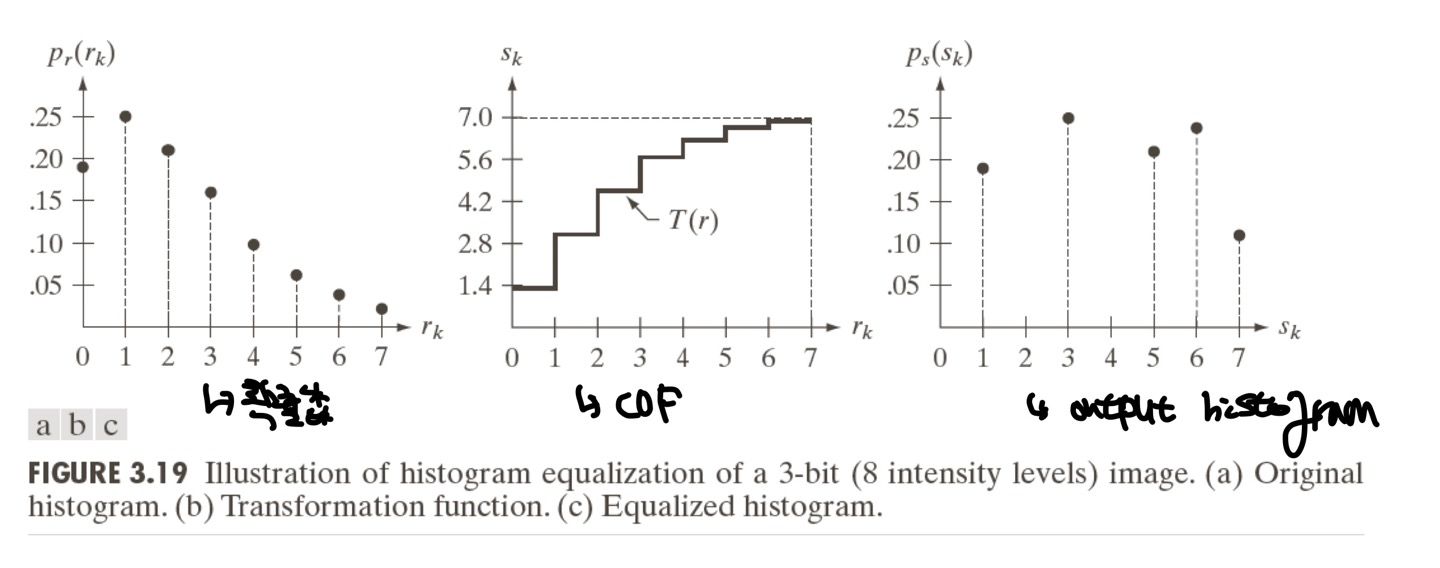
위의 그림은 각 Image의 Pixel값에 따라서 Histogram distribution을 확인할 수 있습니다.

맨 오른쪽의 Histrogram distribution이 Pixel값마다 비슷한 것을 볼 수 있습니다.
Histogram distribution이 equalized되면 화질이 더 좋다는 것을 알 수 있게 됩니다.
(하지만 Spatial Information을 얻을 수 없는 단점이 존재합니다)

먼저 수학적 수식을 이해하고 설명드리겠습니다.
$r_k$ : pixel값을 의미합니다.(Intensity of a digital Image f(x,y))
$n_k$ : Image에서 $r_k$에 해당하는 개수를 의미합니다.(the number of pixels in f with intensity $r_k$

Unnormalized Histogram

h($r_k$) = $n_k$는 unnormalized한 식을 나타냅니다.
좀 더 자세히 설명하자면 $r_k$개수를 단순히 $n_k$로 Histogram으로 표현하게 된 것 입니다.

Normalized Histogram

p($r_k$) = h($r_k$) / (NxM) = $n_k$ / (NxM)는 normalized한 식을 나타냅니다.
먼저 NxM은 Image의 size를 나타냅니다.(resolution이 되겠네요.)

그렇다면, $n_k$를 NxM으로 나눠주면 $r_k$를 뽑을 확률이 되겠지요?
왜냐하면 $n_k$ 자체가 $r_k$를 가지고 있는 개수를 의미하니까요.

이러한 것을 PDF(Probability Density Function)이라고 불리웁니다.
그러면 $\sum_{}^{}$$p_k$/(NxM) = 1이 되는 것을 알 수 있습니다.(확률을 모두 더한 값입니다.)

Goal

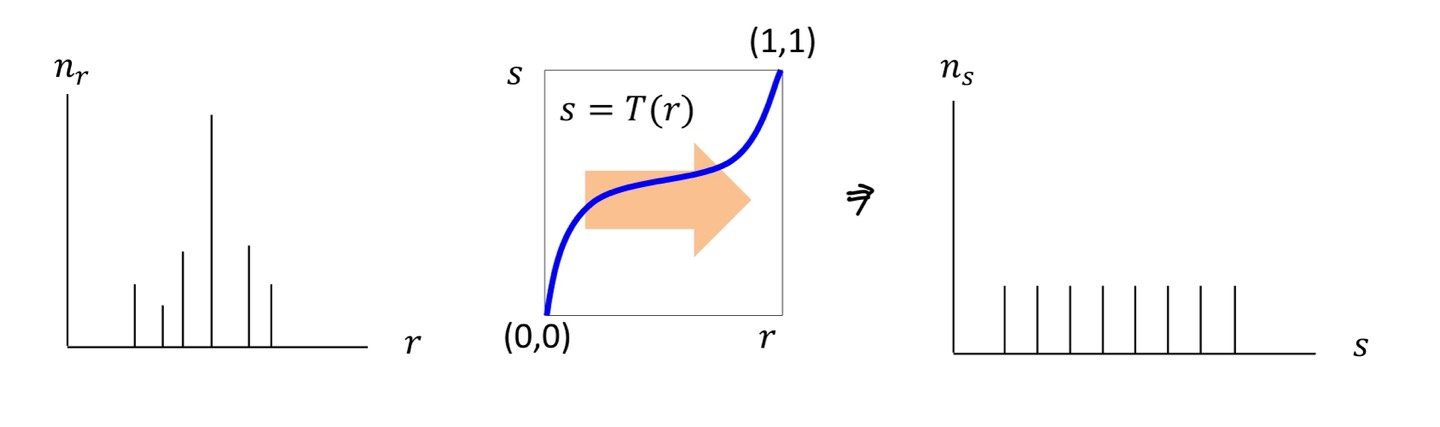
우리는 앞선 내용인 Intensity Transformation을 보면 어떠한 Transformation Function을 통해 Image를 변환시키는 것을 볼 수 있었습니다.
Histogram Equalized도 마찬가지로 Transformation Function을 통해서 진행하게 됩니다. 그러면 Histogram을 Equalized시키는 Transformation Function을 얻는 것이 목표입니다.

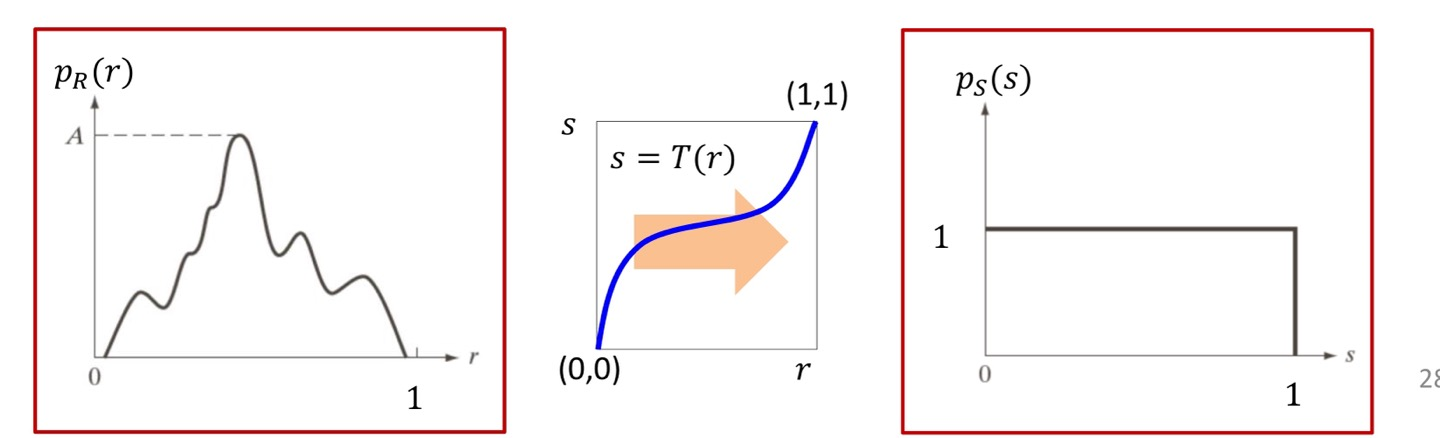
Continuous Case

먼저 Transformation Function을 얻기 전에, Image의 각 Pixel값은 discrete한 값만을 가지고 있지만 Continuous Case라고 가정을 하고 Function을 얻어보도록 하겠습니다.

위의 그림안에 있는 식으로 Transformation Function을 정의했습니다.

결과만 살펴보자면 Function은 $n_k$에 대한 누적값인 CDF(r)로 표현이 됩니다.
CDF(Cumulative Distribution Function)으로 누적 분포 함수값을 나타냅니다.

Transformation Function(s) = $\sum_{i=0}^{\ L-1}$ $P_r$(t) 로 표현됩니다.

그러면 $r_k$를 뽑을 확률을 k가 2라면 $\sum_{i=0}^{\ 2}$ $p(r_k)$로 Function을 정의 할 수 있겠네요.

Discrete Case

저희가 다루는 Image는 Continuous한 값이 아닌 Discrete한 값을 가지고 있습니다.

Continuous의 Transformation Function에서 (L-1)의 값을 곱해주기만 하면 Discrete한 값에서 Function을 구할 수 있게 됩니다.

즉, (L-1)x$\sum_{i=0}^{\ L-1}$ $P_R$($r_i$) 로 Function을 구할 수 있습니다.

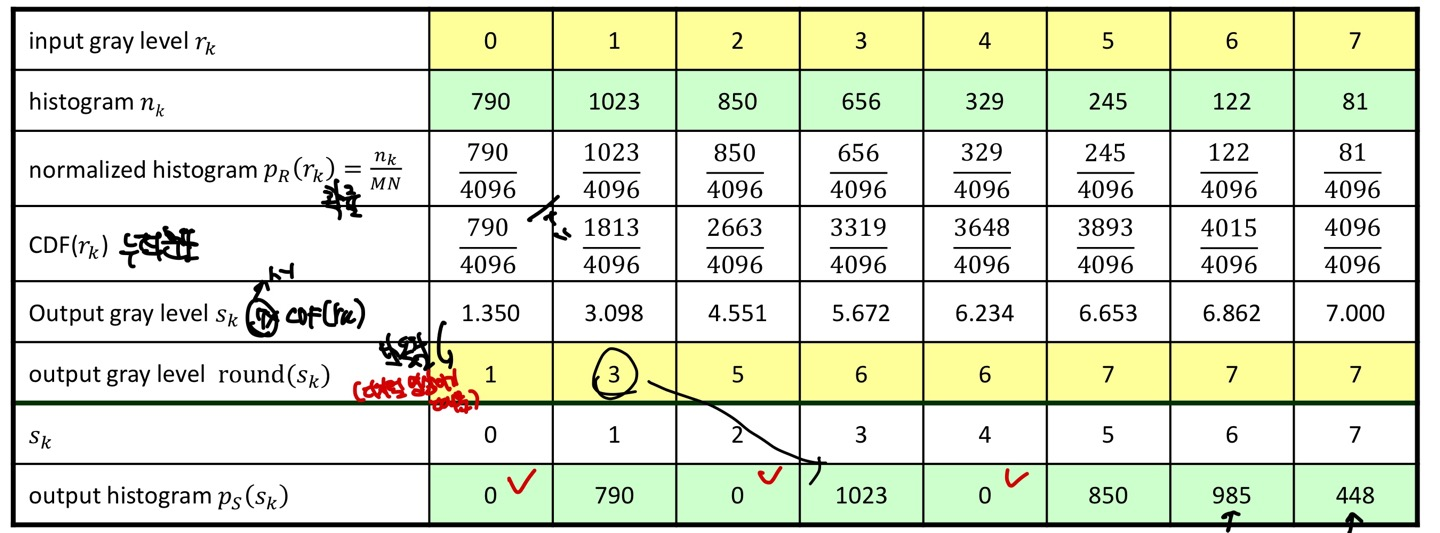
밑의 그림은 위의 설명한 식을 그대로 적용한 Histogram Equalized를 적용한 내용을 간편하게 표현했습니다.
3개의 bit를 쓰는 Image이고, Image Resolution은 64 x 64로(4096 pixels)가 있습니다.

다음은 파이썬으로 히스토그램 평활화를 수행하는 코드입니다.

import numpy as np
import cv2 as cv
import sys

img1 = cv.imread('dgu_night.png',0)

# img를 불러오지 못하면 실행종료
if img1 is None:
    sys.exit('Do not read the file')

def histogram_equalized(img):
    height, width = img.shape
    img_size = height * width # 이미지 크기
    
    # histogram n_k
    pixels = np.bincount(img.ravel(), minlength = 256) # 각 픽셀의 개수 구하기(0~255니까 minlenght = 256)
    print('픽셀 개수 :', pixels)
    
    # normalized histogram
    pixels = pixels / img_size 
    print('픽셀 확률 :', pixels)
    
    # CDF x (l-1)
    CDF = [0] * (len(pixels))  # CDF값 저장할 공간
    
    CDF[0] = pixels[0]
    
    for index in range(1, len(pixels)):
        CDF[index] = CDF[index - 1] + pixels[index]
    
    # round((L-1) * CDF)
    CDF = np.round(255 * np.array(CDF))
    
    print('(L-1) x CDF :', CDF)
    
    # output histogram
    equalized_image = img.copy() 
    
    for i in range(len(CDF)):
        equalized_image[img == i] = CDF[i]
    
    return equalized_image
img = histogram_equalized(img1)
cv.imshow('original Image', img1)
cv.imshow('Equalized Image', img)
cv.waitKey()

---

Pointwise Operations

Image의 size가 똑같다고 가정하고 Image들에 대한 계산을 할 수 있습니다.

Operation의 종류는 Addition, Subtraction, Multiplication, Division이 있습니다.
Addition은 I(x,y) = a(x,y) + b(x,y)로 표현되며, 똑같은 위치(x,y)의 Pixel값을 더해준다고 보시면 됩니다.

우리가 어떠한 Image를 사진을 찍으면, Image에는 Image에 대한 정보와 Noise가 같이 들어간다고 합니다.
이것을 수식으로 나타낸다면, $f_i$(x,y) = g(x,y) + $n_i$(x,y)로 표현이 됩니다.

먼저 우리가 받아들여야 할 식이 있습니다.
E[$n_i$(x,y)] = 0, E[$n_i$$(x,y)^2$] = $σ^2$ 로 표현합니다.

g(x,y) : Image에 대한 정보
$n_i(x,y)$ : Noise
$f_i(x,y)$ : i번째 찍은 영상
$σ^2$ : image가 얼마나 Noise가 있는지 나타내줍니다.(Noise를 수치화 시킨 값 입니다.)

우리는 여러 개의 Image들을 합쳐서 averaging 하게되면, Noise값을 낮출 수 있습니다.

증명 과정을 나타내어 보겠습니다.

위의 증명과정을 보게되면 결국 $σ^2$/k의 결과 값을 볼 수 있습니다.

만약 k개의 영상을 합쳤다고 생각하면 Noise를 k만큼 나눠준 값으로 작아진 Image를 볼 수 있습니다. (생각보다 신기함)

---

Image Processing을 배우면서 생각보다 유도과정을 이해하려면 Probability와 Linear Algebra를 잘 이해하고 있어야 할 것 같습니다..

아무튼 읽어주셔서 감사합니다 ~~ :>