통계학
- 많이 쓰이는 SciPy 알고 있으면 빠르게 쓸 수 있음!!
scipy
│
├── stats # 통계 분석과 확률 분포 관련 함수 제공
│ ├── norm # 정규분포 관련 함수 (PDF, CDF, 랜덤 샘플링 등)
│ │── uniform # 균등분포
│ │── bernoulli # 베르누이 분포
│ │── binom # 이항분포
│ ├── ttest_ind # 독립 두 표본에 대한 t-검정
│ ├── ttest_rel # 대응표본 t-검정
│ ├── mannwhitneyu # Mann-Whitney U 비모수 검정
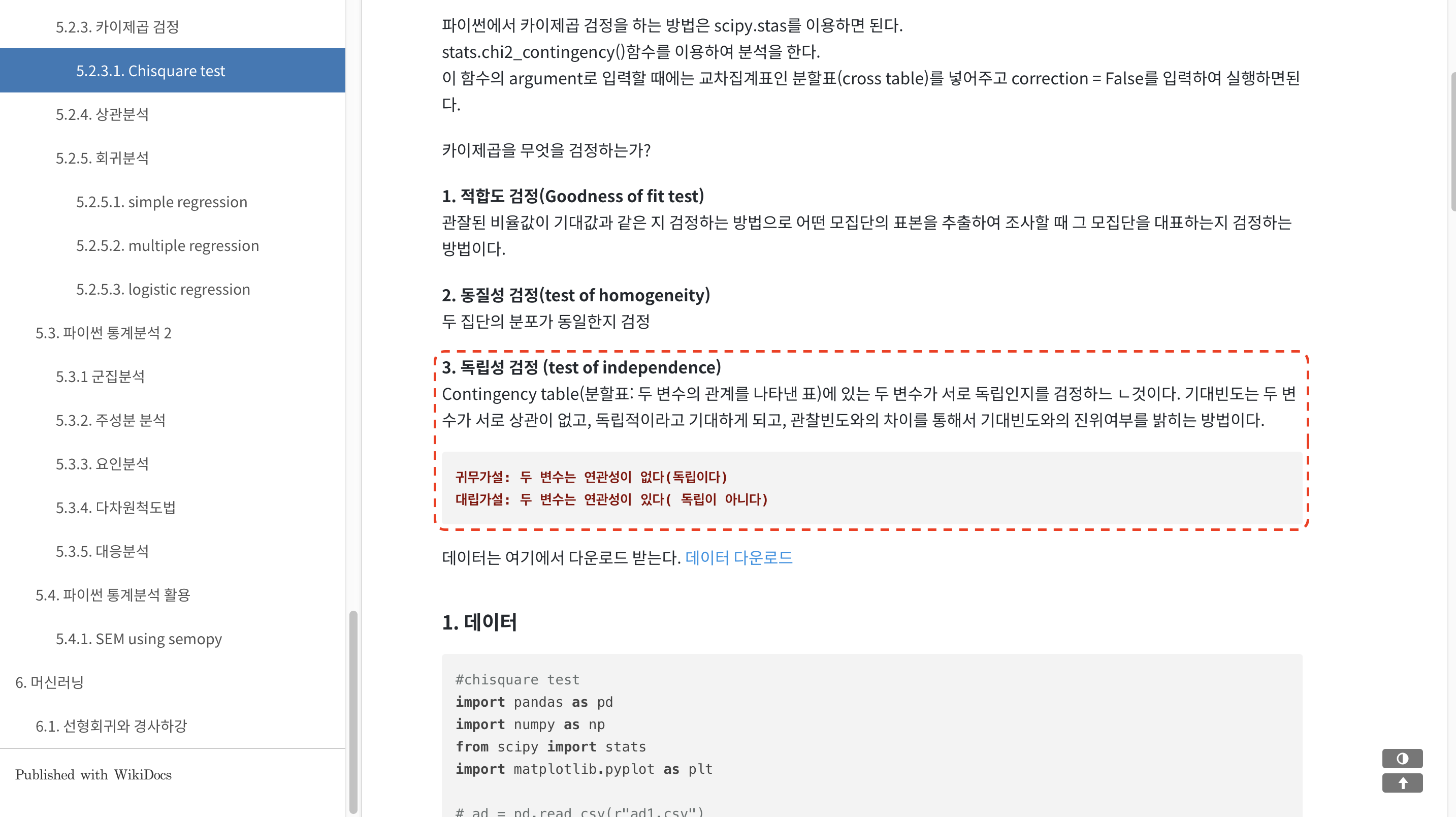
│ ├── chi2_contingency # 카이제곱 독립성 검정
│ ├── shapiro # Shapiro-Wilk 정규성 검정
│ ├── kstest # Kolmogorov-Smirnov 검정 (분포 적합성 검정)
│ ├── probplot # Q-Q plot 생성 (정규성 시각화)
│ ├── pearsonr # Pearson 상관계수 계산
│ ├── spearmanr # Spearman 순위 상관계수 계산
│ └── describe # 기술 통계량 제공 (평균, 표준편차 등)
# 불러올 때
scipy.stats.binom # 이항분포 불러오기
scipy.stats.norm # 정규분포 불러오기- 라이브러리와 같이 많이 쓰이는 메소드
method
├── rvs(size = n) # 난수를 생성
├── pmf(k) # 이산형 분포의 특정 정수(k)에서의 확률 값을 계산
├── pdf(x) # 연속형 확률 변수에서 특정 x값에서의 확률 밀도(y)를 계산
├── cdf(x) # 특정 값 x 이하의 확률을 계산(=표준정규분포표)
└── ppf(q) # 누적확률 q에 해당 하는 값 x를 반환
# 난수 생성하고 싶을 때 (평균 100, 표준편차 15, 데이터수 25)
(scipy.)stats.norm.rvs(loc=100, scale=15, size=25)
# 특정 정수에서의 확률 값(예; 가위바위보 - 시행횟수 6, 확률 1/3) 가위(0) 일때
(scipy.)stats.binom.pdf(0, n=6, q=0.333...)
# 특정 위치의 확률 알고 싶을 때(평균 100, 표준편차 15, 데이터수 25) 에서의 x= 87 일때
(scipy.)stats.norm.pdf(x=87, loc=100, scale=15)
# 특정 위치의 누적확률을 알고 싶을 때(평균 100, 표준편차 15, 데이터수 25) 에서의 x= 87 일때
(scipy.)stats.norm.cdf(x=87, loc=100, scale=15)
# 특정 누적확률에 해당하는 x 값을 알고 싶을 때(평균 100, 표준편차 15, 데이터수 25) 에서 q = 0.94 일때
(scipy.)stats.norm.ppf(q=0.94, loc=100, scale=15)
통계에서는 라이브러리와 메소드를 같이 많이 사용하니까 메소드를 많이 적어보고 외우는 것이 좋을 듯!!
그리고 메소드와 라이브러리가 반복되기 때문에 직접 예시를 적어보면서 작성하는 것이 더 빠른 시간내에 익힐 수 있을 듯 하다.
통계학 기초
연습문제 오답 - 3주차
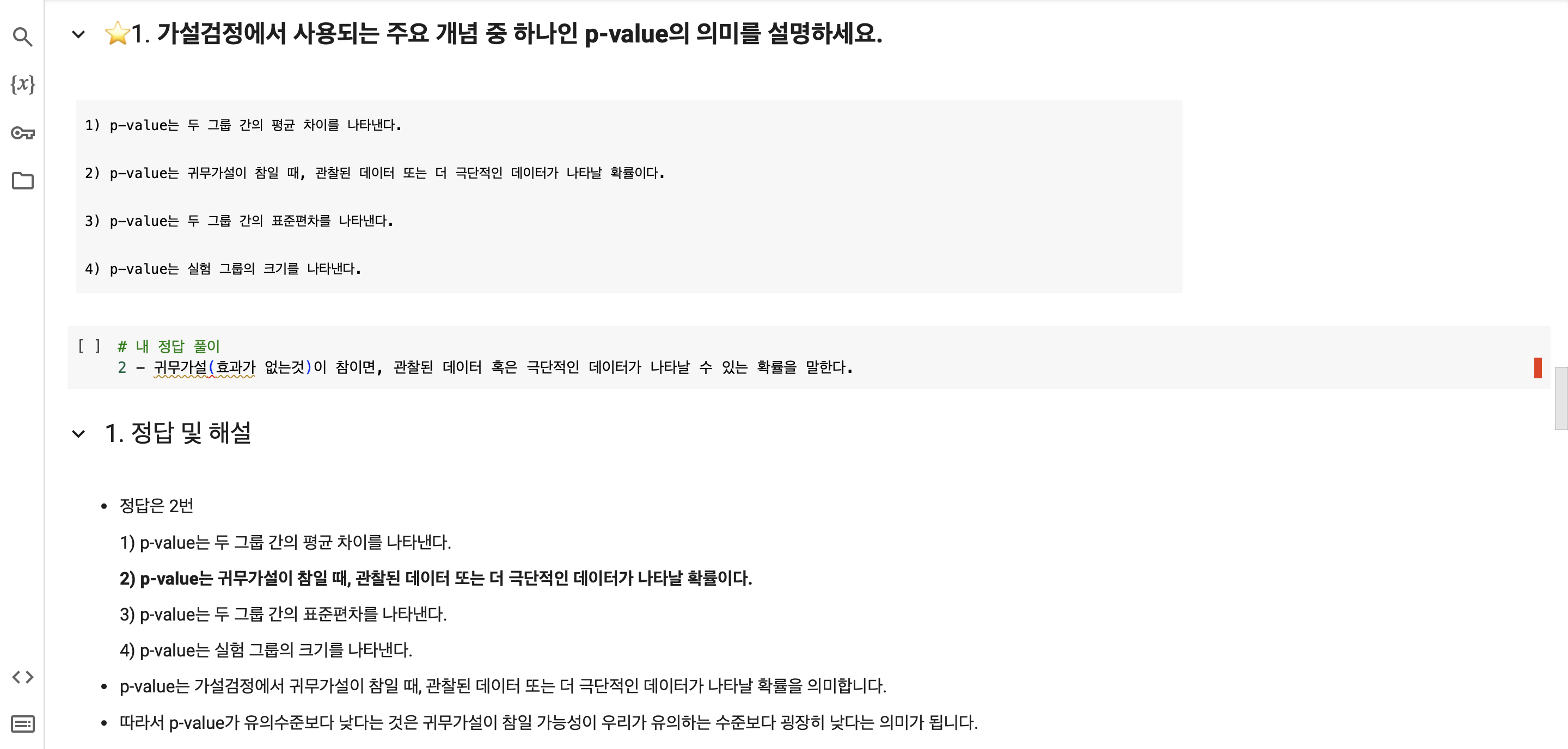
p-value는 예외가 일어난 확률을 나타낸다.
보통의 기준은 0.05 = 5% 이다.
p-value가 0.05(기준)보다 작으면 두 집단이 연관되어 있어 통계가 유의미하다는 뜻이고,
0.05(기준)보다 크면 두 집단은 같은 집단이거나 서로 다른 집단인 것이다.

- 귀무가설; (영가설) 두 집단은 연관성이 없다. / 예) 새로운 기술은 현재 있는 기술보다 효과적이지 않다.
- 대립가설; 두 집단은 연관성이 있다. / 예) 새로운 기술은 효과적이다.
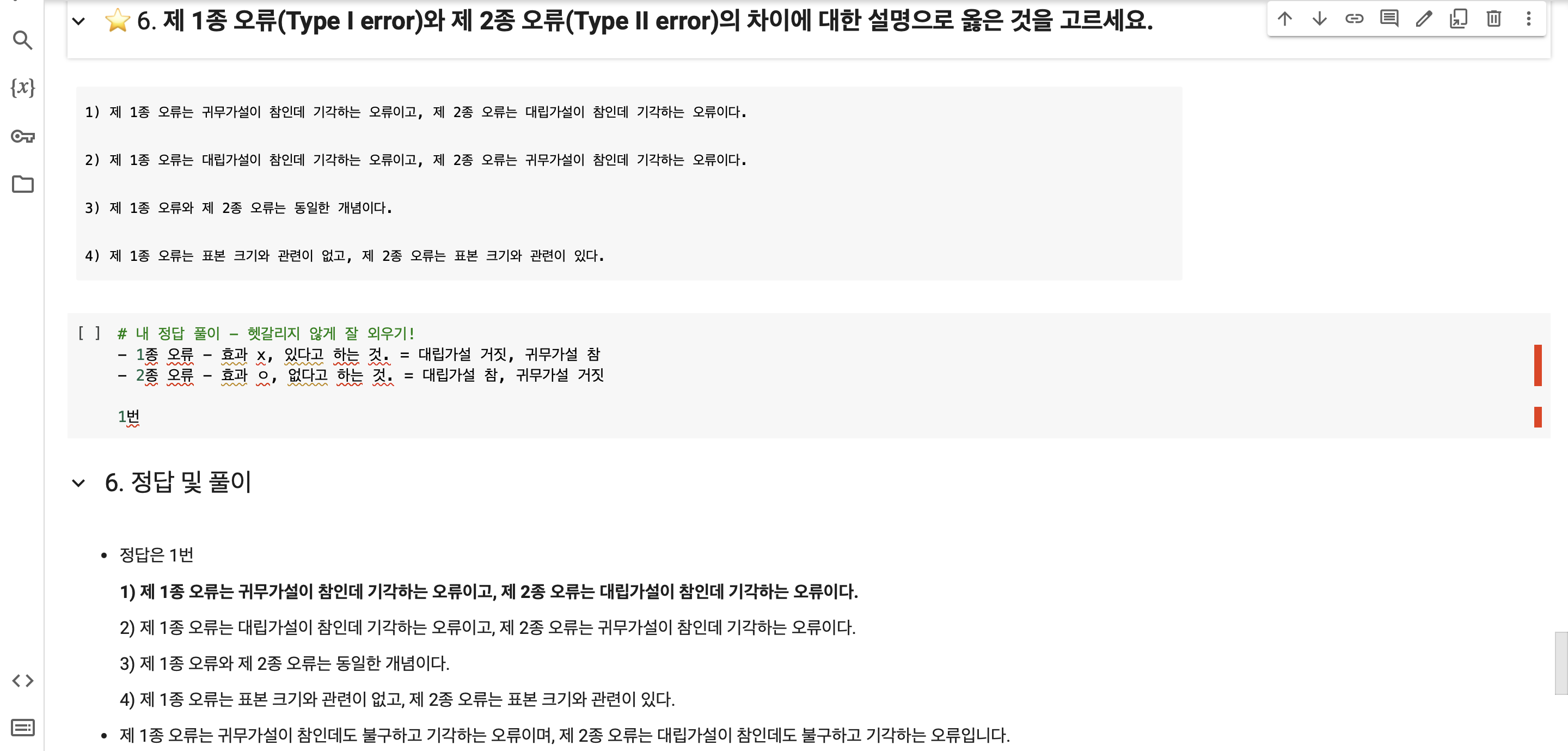
- ⭐️제 1종 오류와 제 2종 오류⭐️
1. 제 1종 오류
- 위양성
- 귀무가설 참 / 대립가설 거짓
- 예) 효과가 없는데도 있다고 한 것 (잘못된 긍정)
<해결방법> - ⍺(alpha)의 값을 최대한 줄이자
- ⍺(alpha)란? 1종 오류가 발생할 수 있는 확률! = 유의수준과 같은 말 - 보정방법 채택 (본페로니, 튜키, 던넷, 윌리엄스 등) ; 대표적으로는 본페로니 보정 사용
2. 제 2종 오류
- 위음성
- 귀무가설 거짓 / 대립가설 참
- 예) 효과가 있는데도 없다고 한 것 (잘못된 부정)
<해결방법>
- β(beta)의 값을 줄이기 어려움
- β(beta)란? 2종 오류가 발생할 수 있는 확률
- 직접 통제할 수 없기 때문.. - 그나마 시도해볼만한 방법 => 표본크기(n)이 커질수록 β(beta)가 작아짐
- BUT, ⍺(alpha) <-> β(beta) 서로 상충관계(하나가 증가하면 다른 하나는 무조건 감소하는 관계)로 한 쪽이 너무 맞으면 다른 쪽이 너무 높아짐
기타 - LaTex 문법
어제 튜터님께서 말씀해주신 Greek Letter의 관한 코드를 찾아서 대표적인 몇가지를 적어보았다.
"LaTex 문법"이라는 제목을 클릭하면 해당 코드가 적혀있는 구글 코랩으로 넘어가게 된다.
나도 해당 자료는 Matplotlib Tutorial - 파이썬으로 데이터 시각화하기라는 위키독스에서 참고하여 코드를 작성해보았다.
기본적으로 그리스 문자를 삽입하려고 하면 항상 두개의 $$(달러)표시안에 있어야 하며 '\...' 원하는 것 앞에 \(역슬래시)를 붙여서 사용해야 한다.
=> ⍺를 넣고 싶다면 파이썬에서는 $\alpha$ 로 입력해야 하는 것이다.
지금 velog에서도 $와 \ 표시가 글을 적는데도 인식이 되어 기호 그대로 쓴다고 역슬래시를 하나 더 추가해주었다.