통계학 기초

단순선형회귀

• 한 개의 독립 변수(X)와 종속 변수(Y)의 관계를 직선으로 모델링하는 방법
  

출처: 블로그

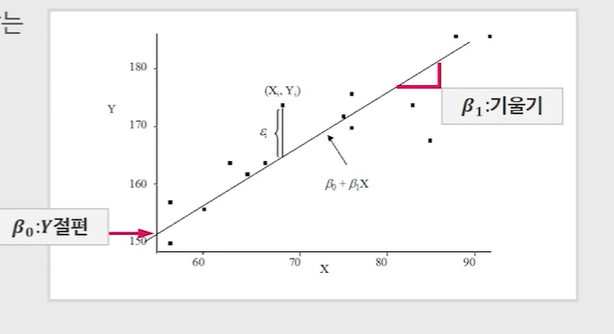
• 회귀식
  $Y = \beta_0 + \beta_1X$
  $\beta_0$ : 절편
  $\beta_1$ : 기울기

  $≈ y = ax + b$ 1차 함수
  $b$ : $y$절편
  $a$ : 함수의 기울기

  💡쉽게 말해 1차 함수의 양상을 띄고 있는 모델

• ⭐️특징
  독립변수의 변화에 따른 종속변수의 변화를 설명하고 예측
  데이터가 직선이랑 비슷할 때 사용 (반대로, 직선이 아닐 때는 적합하지 않음)
  간단한 해석

---

단순선형모델 파이썬 실습

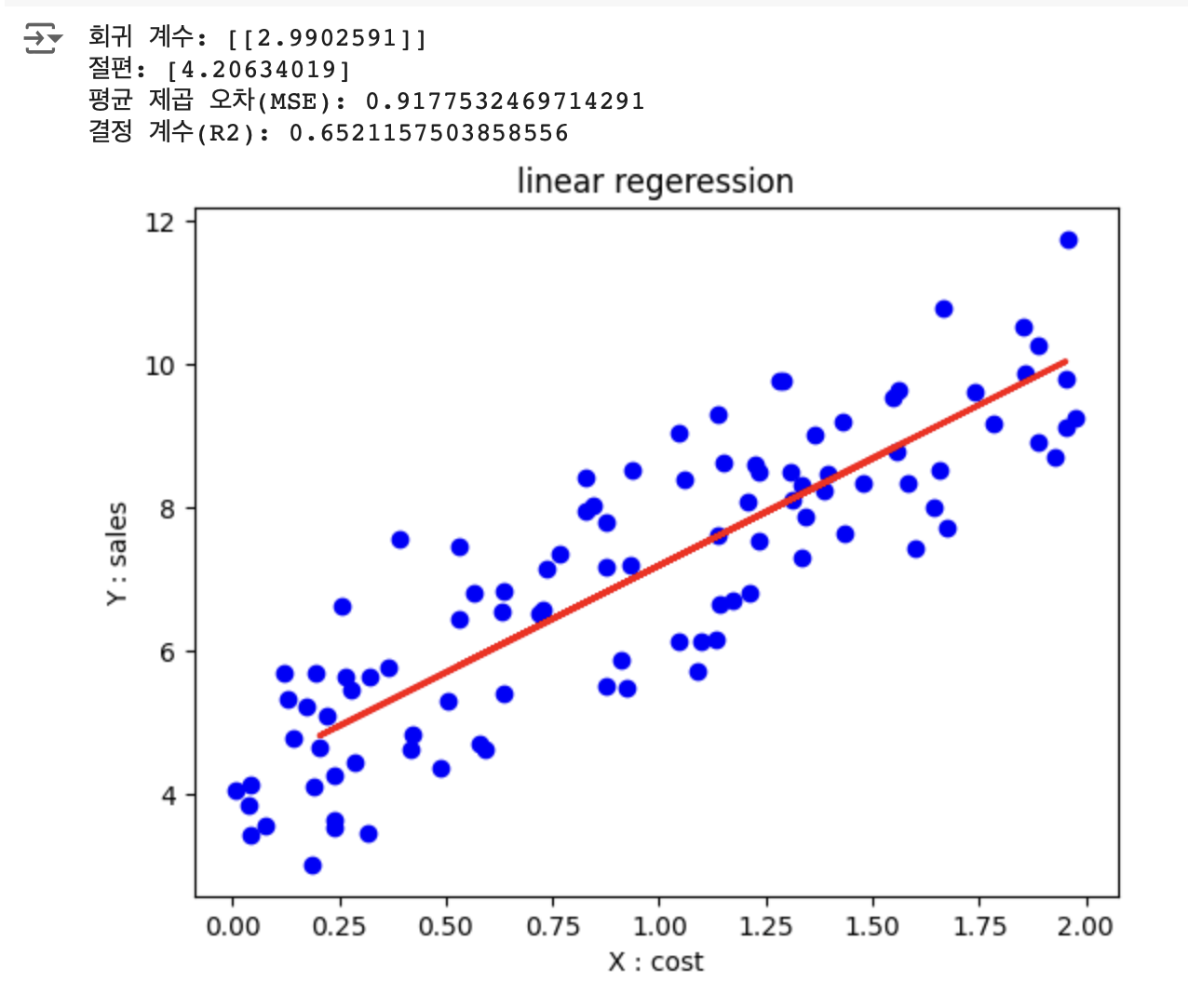
예) 광고비(X)와 매출(Y)의 관계
-> 현재 광고비를 바탕으로 예상되는 매출 예측 가능

• 회귀계수 = 기울기

• MSE(Mean Squared Error) 평균 제곱 오차?
  예측된 값들이 실제 값에 얼마나 가까운지를 측정하며, 값이 작을수록 모델의 예측 정확도가 높음을 의미
  MSE 계산 공식 (자세한 내용은 제목 클릭)
  $MSE = (1/n) * \Sigma(P_i - A_i)^2$
  - $n$ : 데이터 포인트의 총 수
  - $P_i$ : $i$번째 데이터 포인트에 대한 예측값
  - $A_i$ : $i$번째 데이터 포인트의 실제값
  

• $R^2$($R$ Square) 결정 계수?
  
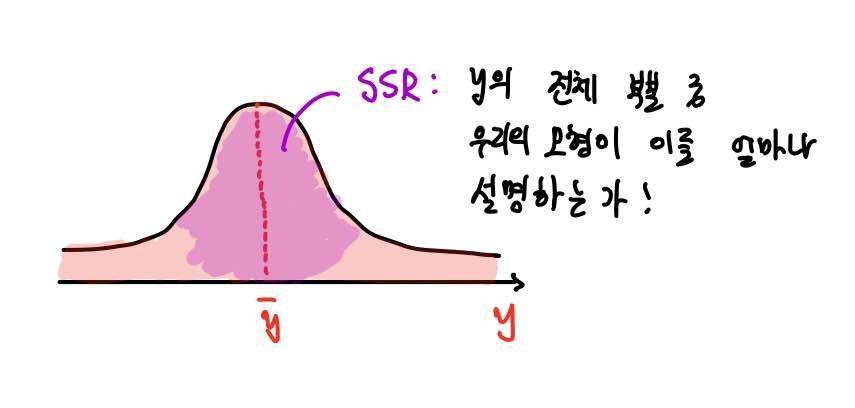
  $R^2$ 계산 공식 (자세한 내용은 제목 클릭)
  $R^2 = SSR / SST = 1 - SSE/SST$
  - $SSR$ : 설명 가능한 변동
  - $SSE$ : 설명 불가능한 변동
  - $SST$ : 총 변동 = $SSR + SSE$

$R^2$ : $0 ≤ R^2 ≤ 1$

• $R^2 = 0$ ; x와 y는 어떠한 선형 상관관계도 없음
• $R^2 = 1$ ; x와 y는 완벽한 선형 상관관계
  0에 가까울수록 선형 상관관계의 정도가 없다
  1에 가까울수록 선형 상관관계의 정도가 크다

---

다중선형회귀

• 2개 이상의 독립변수($X_1,X_2,...,X_n$)에 따른 종속변수(Y)의 변화
  

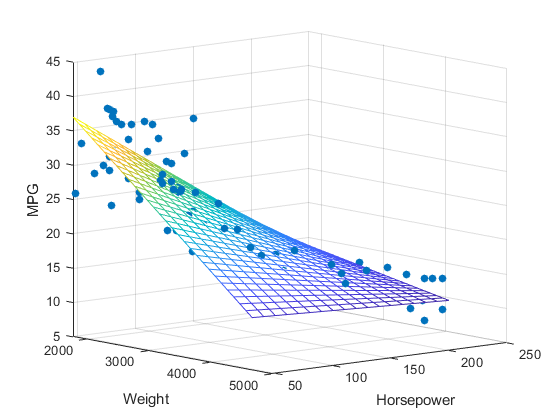
출처: 블로그

• 회귀식
  $Y = \beta_0 + \beta_1X_1 + \beta_2X_2 +...+ \beta_nX_n$
• ⭐️특징
  여러 독립 변수의 변화에 따라 종속 변수 설명하고 예측
  여러 변수의 영향을 동시에 분석할 수 있음
  BUT, 변수끼리 다중공선성 발생할 수 있음

  ⭐️다중공선성⭐️
  

---

⭐️다중공선성⭐️

<설명>

• 두 변수 이상에서 높은 상관관계가 나타나는 것
• 높은 상관관계가 나타나는 변수들이 있으면 그 중 한가지만 분석하는 게 더 좋을 수도!!
  예) 남,여 (남 아니면 당연히 여인데 굳이 둘 다 만들 필요가 있을까??)

<진단 방법>

• 변수들의 상관계수 계산 -> 상관계수 높은 변수들 확인 (기준 설정, 보통은 약 0.7)
• 분산 팽창 계수(VIF) 계산 -> $10 ≤ VIF$ (10보다 결과값이 높은지 확인)

  분산 팽창 계수(VIF)❓
  대략 어떤거다 하고 알고 있으면 될 듯하다
  

  from statsmodels.stats.outliers_influence import variance_inflation_factor
  import statsmodels.api as sm
  # 독립 변수 행렬
  X = data[['X1', 'X2', 'X3']]
  # 상수항 추가
  X = sm.add_constant(X)
  # VIF 계산
  vif = pd.DataFrame()
  vif["변수"] = X.columns
  vif["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
  # vif 결과 출력
  print(vif)

<해결 방법>

• 상관계수가 높은(약 0.7) 변수들 중 하나 제거☠️
• 주성분 분석(PCA) 활용 -> 변수들을 효과적으로 줄이기

  주성분 분석(PCA)❓
  대략 이런거다.. 하고 알고 있으면 될 듯 하다.
  

  	# 필요한 라이브러리 불러오기
  from sklearn.decomposition import PCA
  from sklearn.datasets import load_iris
  import pandas as pd
  	# Iris 데이터셋 불러오기
  iris = load_iris()
  X = iris.data
  columns = [f'feature_{i+1}' for i in range(X.shape[1])]
  df = pd.DataFrame(X, columns=columns)
  	# PCA 모델 생성 및 학습
  pca = PCA(n_components=2)  # 주성분을 2개로 설정
  X_pca = pca.fit_transform(X)
  	# 결과 출력
  explained_variance_ratio = pca.explained_variance_ratio_
  print(f"주성분의 설명된 분산 비율: {explained_variance_ratio}")
  	# 주성분으로 변환된 데이터프레임 생성
  columns_pca = ['Principal_Component_1', 'Principal_Component_2']
  df_pca = pd.DataFrame(X_pca, columns=columns_pca)
  	# 주성분이 추가된 데이터프레임 출력
  df_with_pca = pd.concat([df, df_pca], axis=1)
  print(df_with_pca.head())

---

다중선형회귀 파이썬 실습

시각화는 너무 어려워서 강의에서 생략되었다
예) 다양한 광고비(TV, Radio, Newspaper)과 매출 간의 관계 분석
-> 현재 광고비(TV, Radio, Newspaper)을 바탕으로 예상되는 매출을 예측 가능

X_train, X_test 차이
아직 머신러닝을 배우지 않아서 모르는 개념이라 궁금해서 찾아봤다.
train과 test의 차이는 학습과 실제 시뮬레이션 차이인듯 싶다.
즉, train = 훈련하다하는 뜻이다.

다음과 같은 설명을 통해 머신러닝에 학습된 내용과 실제 테스트를 했을 때 적절한 것 외에 나올 수 있는 현상을 알 수 있었다.

---

범주형 변수

• 문자형 데이터로 이루어져있는 변수 => 범주형 변수
  

출처: 블로그

• 범주형 변수 종류
  문자열로 되어있는 범주 -> 예) 상호명, 성적 등급 등

🔢순서가 있는 범주형 변수
크기 비교 (소,중,대), 성적(1등급, 2등급, 3등급, ...) 과 같이 순서가 정해져 있는 경우
임의의 숫자로 변환 (단, 순서가 잘 반영될 수 있도록 숫자로 변환)
예) 1등급 -> 0, 2등급 -> 1, 3등급 ->2 ,...

😵‍💫순서가 없는 범주형 변수
지역(서울,경기,광주,부산,...), 성별(남,여) 와 같이 순서가 정해져 있지 않은 경우
성별과 같이 2개인 변수 -> 임의의 숫자로 바꿔도 OK
지역과 같은 3개 이상인 변수 -> pandas(get_dummies) 함수 활용하여 구현
예) 서울 = [1,0,0,0], 경기 = [0,1,0,0], 광주 = [0,0,1,0], 부산 = [0,0,0,1]

---

범주형 변수 파이썬 실습

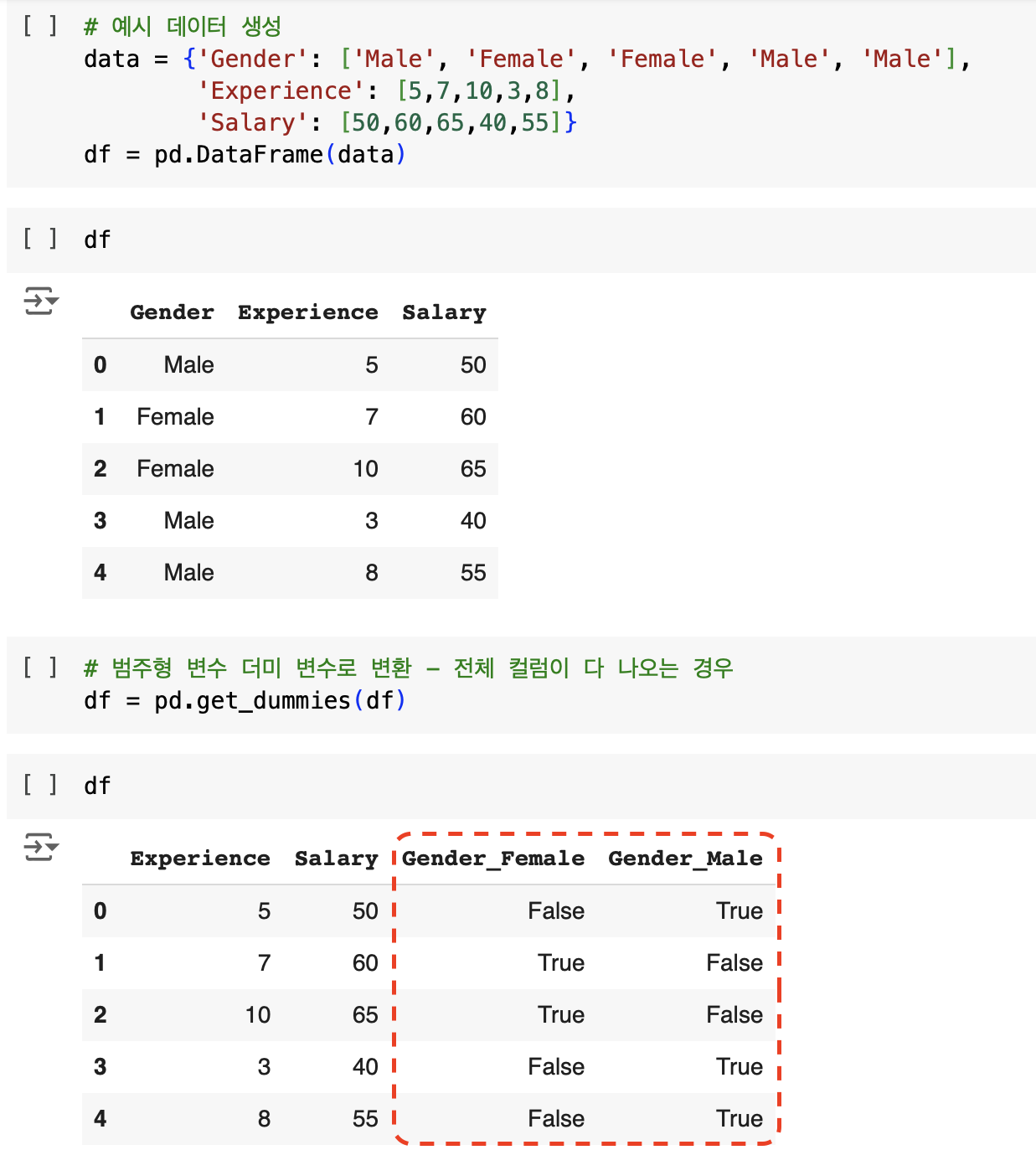
예) 성별, 근무 경력과 연봉 간의 관계

• 성별, 근무 경력 (독립 변수) => 성별(범주형 변수)
• 성별 => 더미 변수 (get_dummies)로 변환
  

더미 변수로 변환 과정

# 전체 데이터 프레임에서 더미 변수로 변환
df = pd.get_dummies(df)

# df와 다르게 출력하기 위함 임시 df2 설정
# 더미 변수 변환 후 하나만 남도록 설정
df2  = pd.get_dummies(df, drop_first=True)

---

다항회귀, 스플라인 회귀

다항회귀

• 독립 변수 - 종속 변수 간의 관계가 선형이 아닐 때
  

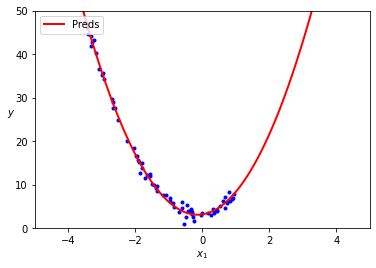
출처: 블로그

• ⭐️특징
  데이터가 곡선적 경향을 따를 때
  비선형 관계를 모델링
  고차 다항식의 경우 과적합(overfitting) 위험이 있음 - 원글의 "X_train, X_test 차이 부분 참고"

---

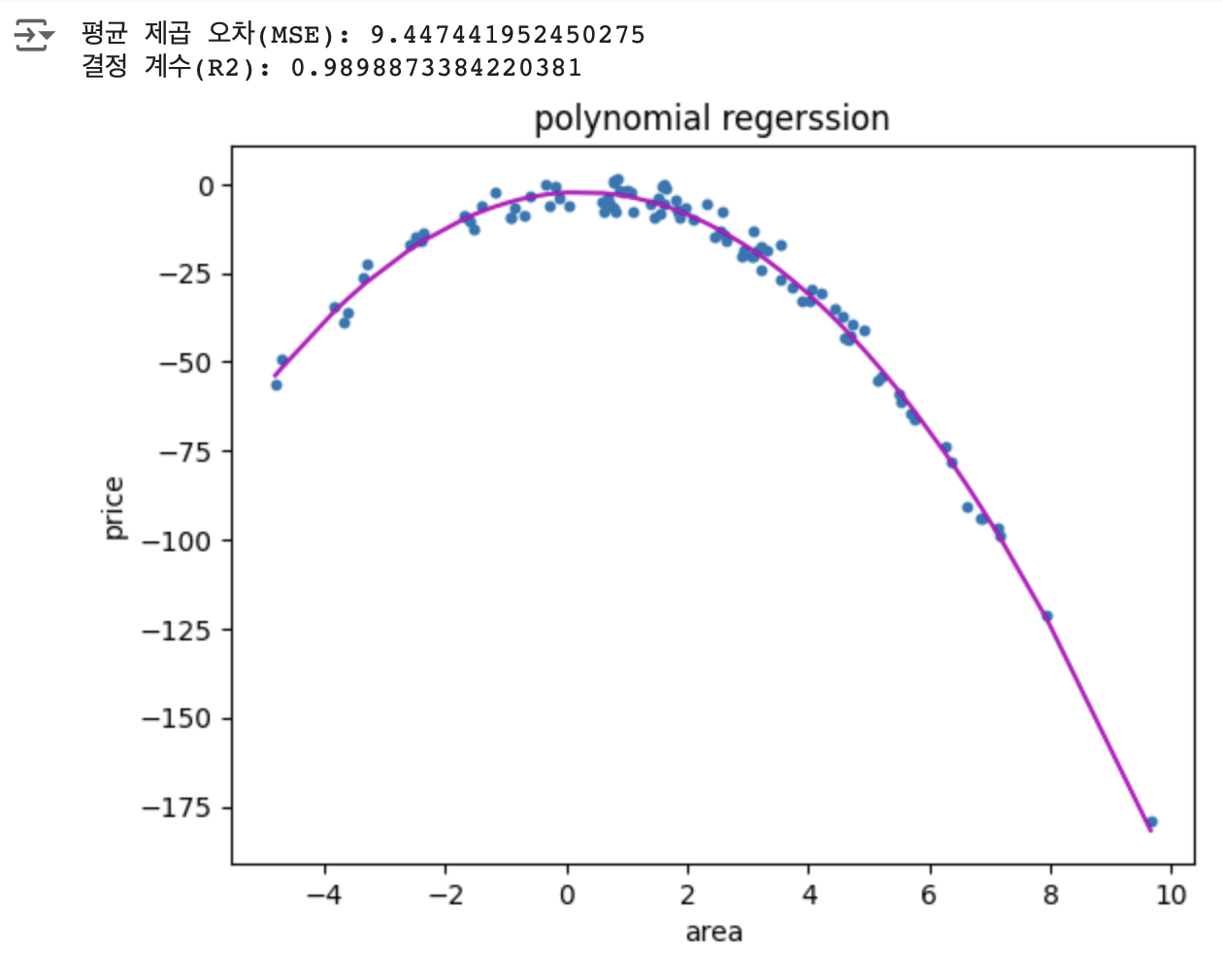
다항회귀 파이썬 실습

스플라인 회귀는 어려워서 강의에서 생략
예) 주택 가격 예측(면적과 가격 간의 비선형 관계)

---

스플라인 회귀

• 데이터가 전체적으로 다른 패턴을 보일 때 사용
  

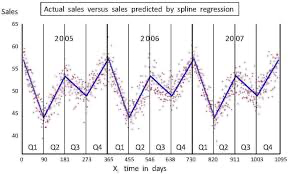
출처: 리서치

• ⭐️특징
  독립 변수의 구간별로 다른 회귀식을 적용하여 복잡한 관계를 모델링
  = 구간마다 다른 다항식 사용 -> 매끄러운 곡선 생성
  복잡한 비선형 관계 유연하게 모델링
  ⭐️적절한 매듭점(knots)를 잡는 것이 중요!

---

연습문제

오늘은 다 맞아서 오답할게 없다!! 대신 오늘 배운 내용에 대해서 조금 더 자세히 알고자 했다.