최단 경로 문제(Shortest path problem)
최단 경로 문제는 그래프에서 시작 정점에서 다른 모든 정점까지의 간선 가중치의 합이 최소가 되는 경로를 찾는 문제이다.
최단 경로 알고리즘은 우리가 흔히 아는 네비게이션에 사용된다. 현재 위치에서 특정 위치까지 가는 거리를 계산하여 가장 빠른 경로를 추천해 줄 수 있다.
최단경로 알고리즘에는 여러 알고리즘이 있지만 대표적으로 3가지만 알아보자.
1. 다익스트라 알고리즘(음의 가중치를 포함하지 않는 최단 경로)
2. 벨만-포드 알고리즘(음의 가중치를 허용하는 최단 경로)
3. 플로이드-워샬 알고리즘(모든 쌍에 대한 최단 경로)
다익스트라(Dijkstra) 알고리즘
음이 아닌 가중치가 있는 그래프를 기준으로 한다. 한 정점에서 모든 정점에 이르는 최단 경로를 모두 구하는 알고리즘이다.
다익스트라 알고리즘의 핵심은 시작 정점이
s, 도착 정점이w,s와w가 인접한 정점을u라고할 때
s->w 로 바로 가는 거리와 s->u->w 로 거쳐서 가는 거리를 비교해 작은 거리를 저장한다.
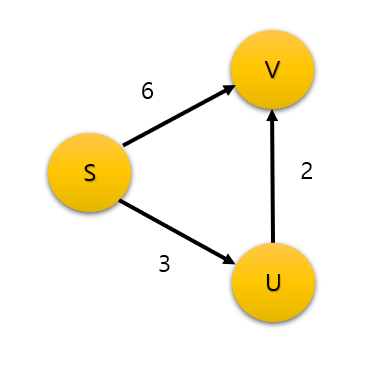
그림을 보면 s->v 의 가중치는 6 이지만 s->u->v 는 5로 더 작은 가중치를 가진다.
단계별 과정
예시를 통해 좀 더 살펴보자.
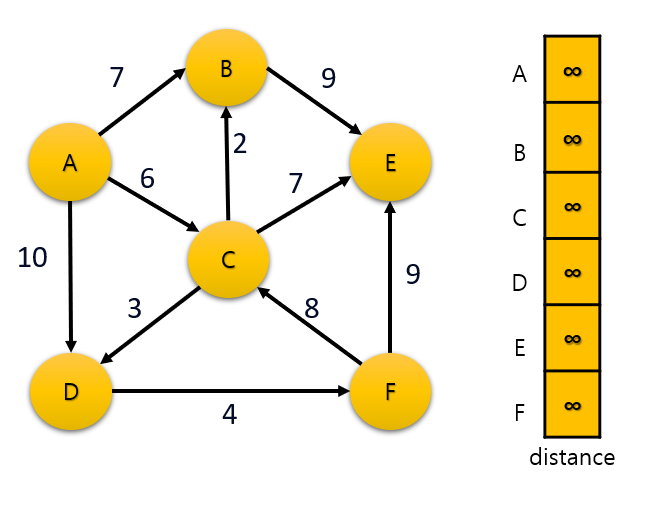
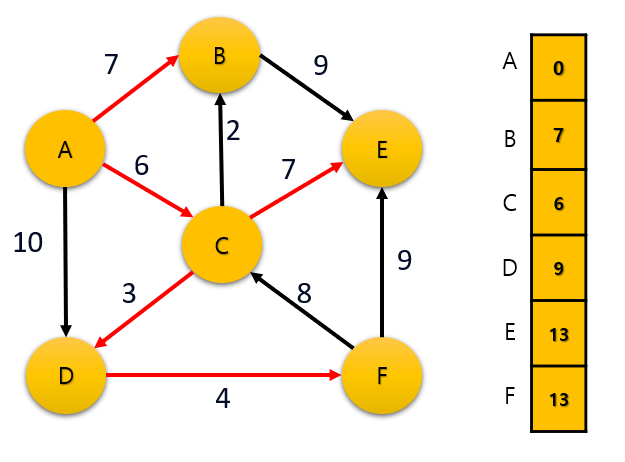
다음과 같은 그래프가 있다고 할 때 A에서 시작해서 모든 정점에 이르는 최단 경로를 구하는 과정을 보자. 전체 최단 경로의 값은 distance 배열에 저장한다.
초기 상태는 전체 distance 의 값을 무한대로 정의한다.
1. A 정점 방문
A 정점 방문시에 정점 A와 인접한 모든 정점의 distance 값을 기존 가중치 값으로 초기화 한다.
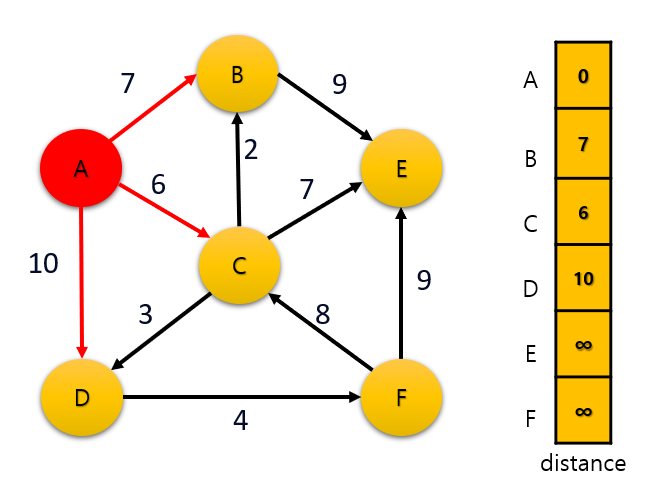
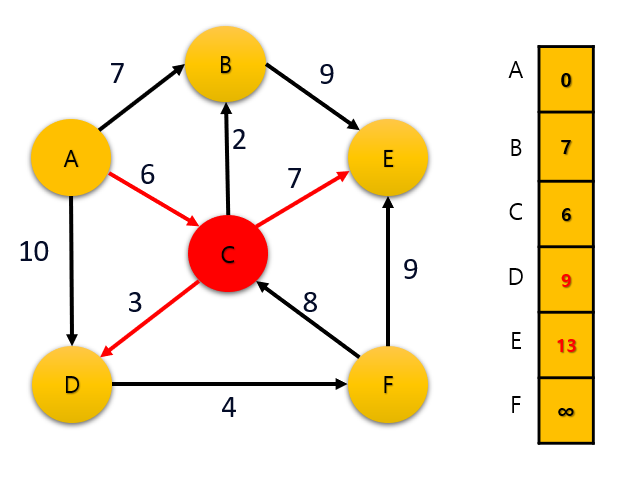
2. C 정점 방문
distance 값 중에서 가장 작은 가중치 값을 가지고 있는 정점 C 를 방문한다.
C 와 인접 한 정점 B , E , D 로 이동하는 경로를 살펴보자.
정점 C 방문시 A->C->B 로 가는 경로는 8 로 A->B 로 가는 경로인 7 이 더 작기 때문에 가지 않는다.
반대로 A->C->D 로 가는 경로는 9 이고 A->D 로 가는 경로는 10 이기 때문에 C->D 의 경로로 이동한다.
3. 나머지 정점
나머지 정점들도 위와 같은 방식으로 방문을 수행한다.
결과를 보면 A->C->B->D->E->F 순으로 방문한다. 값이 같은 경우에는 로직에 따라 다르다.
코드
앞서 이야기 한것을 바탕으로 최단 거리를 구하는 로직을 살펴보자.
weight은 간선의 가중치를 저장한 배열, 시작 정점에서 정점(index)까지의 거리를 저장하는 배열을 distance라고 하면 다음과 같은 식이 성립한다.
if(distance[u] + weight[u][w] < distance[w]) // s->u->w 와 s->w 비교
distance[w] = distance[u] + weight[u][w]전체 코드
C 로 작성한 코드이다. 해당 코드에서 인덱스는 정점을 나타낸다.
weight는 2차원 배열의 인접 행렬 그래프로 정점간의 간선 가중치를 나타낸다.
distance는 시작정점으로부터 최단 경로까지의 거리를 나타낸다.
found는 방문한 정점인지를 나타내는 배열로visited라고도 표현한다.
chooose() 함수는 방문하지 않는 노드 중 가장 작은 거리를 찾는 함수이다.
#include <stdio.h>
#define TRUE 1
#define FALSE 0
#define MAX_VERTICES 6
#define INF 10000000
int weight[MAX_VERTICES][MAX_VERTICES] = { // 인접 행렬
{0, 7, 6, 10, INF, INF},
{INF, 0, INF, INF, 9, INF},
{INF, 2, 0, 3, 7, INF},
{INF, INF, INF, 0, INF, 4},
{INF, INF, INF, INF, 0, INF},
{INF, INF, INF,8, 9, 0}};
int distance[MAX_VERTICES];
int found[MAX_VERTICES];
int choose(int n)
{
int i, min, minpos;
min = INF; // 가장 작은 거리를 저장
minpos = -1;
for (i = 0; i < n; i++)
if (distance[i] < min && !found[i])
{ // 작은 거리 찾기
min = distance[i];
minpos = i;
}
return minpos;
}
void dijkstra(int start, int n)
{
int i, u, w;
for (i = 0; i < n; i++)
{ // 전체 거리 초기화
distance[i] = weight[start][i];
found[i] = FALSE;
}
found[start] = TRUE; // 시작정점 방문
distance[start] = 0;
for (i = 0; i < n - 2; i++)
{
u = choose(n); // u: 새로 방문하는 노드
found[u] = TRUE;
for (w = 0; w < n; w++)
if (!found[w]) // 방문하지 않는 노드 확인
if (distance[u] + weight[u][w] < distance[w]) // s->u->w 와 s->w 비교
distance[w] = distance[u] + weight[u][w];
}
}
void main(){
dijkstra(0, MAX_VERTICES);
for(int i = 0; i < MAX_VERTICES; i++)
printf("%d ", distance[i]); // 0 7 6 9 13 13
}정리
다익스트라 알고리즘은 음의 간선을 제외한 특정 하나의 정점에서 다른 모든 정점으로 가는 최단 경로 알고리즘이다.
현실 세계에서 음의 간선이 존재하지 않아 현실세계에서 사용하기 적합한 알고리즘 중 하나이다.
특히 최단거리를 구할 때 이전까지 구했던 최단 거리 정보를 사용한다는 점에서 다이나믹 프로그래밍 문제로 볼 수 있다.
📕 참고 링크
다음의 링크를 참고했습니다.
https://en.wikipedia.org/wiki/Shortest_path_problem
https://velog.io/@dlgosla/최단경로-알고리즘
https://jina-developer.tistory.com/118
25강 - 다익스트라 알고리즘(Dijkstra Algorithm) [ 실전 알고리즘 강좌(Algorithm Programming Tutorial) #25 ]

