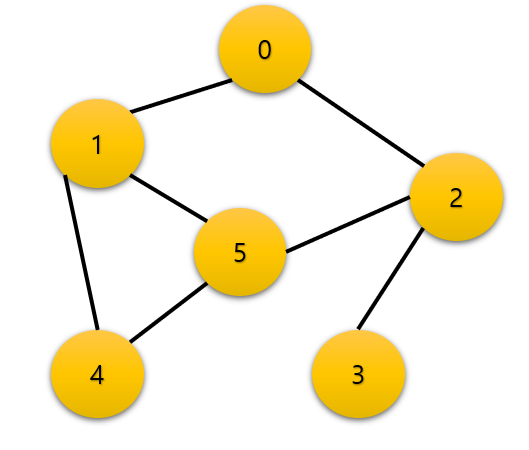
그래프란?
표현하고자 하는 현상이나 사물을 정점(vertex, node)와 연결선, 간선(link, edge)으로 표현한 것을 말한다.
트리와 마찬가지로 비선형 자료구조 중 하나로 트리는 그래프의 일종이다.
기존의 스택, 큐와 같은 자료구조로는 연결망과 같은 복합적인 관계를 표현하기에는 어려움이 있기에 이러한 자료구조를 사용한다.
흔히 말하는 그래프의 예시로는 지하철 노선도를 말할 수 있다. 각각의 역은 노드이고 이를 연결하는 철로는 간선이라 할 수 있다.
그래프 용어
정점 : 데이터를 저장하는 한점. vertex, node 로 불린다.
간선 : 정점을 연결하는 선. link, edge 로 불린다.
차수 : 무방향 그래프에서 하나의 정점에 인접한 정점의 수
단순경로 : 경로 중에서 반복되는 정점이 없는 경로
가중치 : 간선을 지날때의 비용
사이클 : 단순 경로의 시작 정점과 종료 정점이 동일한 경우
그래프 종류와 특징
그래프에는 그래프를 구분 짓는 몇가지 특징이 존재한다.
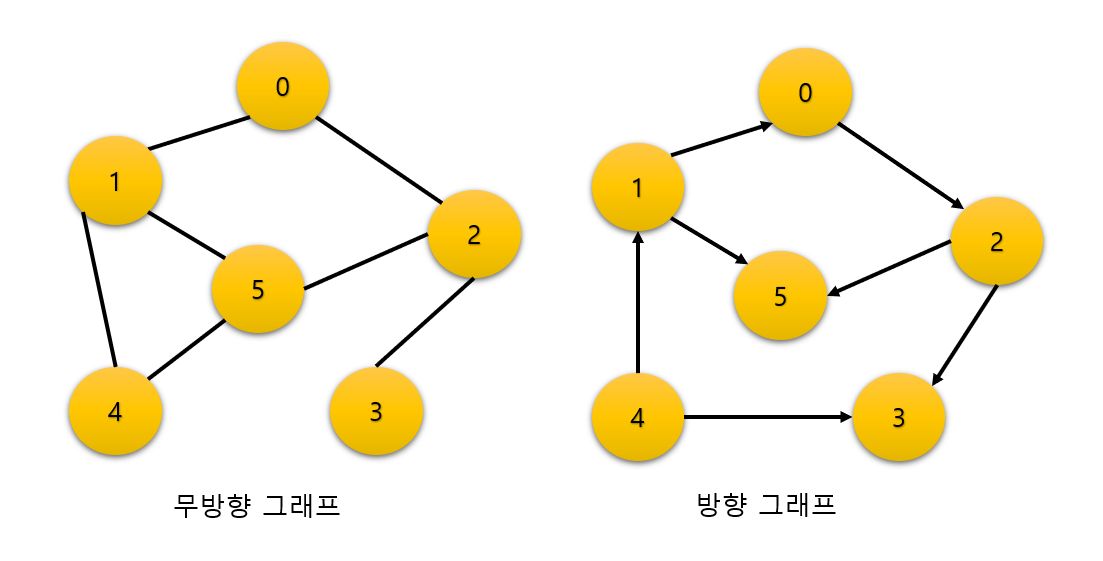
1. 무방향, 방향 그래프
무방향 그래프는 방향이 없는 그래프로 간선을 통해 양방향으로 갈 수 있음을 나타낸다.
표기는 (a, b) 와 같이 표기한다.
방향 그래프는 말그대로 방향이 있는 그래프로 a에서 b로 가는 방향을 a->b와 같이 화살표로 표기한 그래프이다.
이때 a에서 b로만 방향이 존재하면 b에서 a로 가지 못한다.
표기는 a->b를 표기하면 <a, b> 와 같이 표기한다.
따라서 <a, b> 와 <b, a> 는 서로 다른 간선을 의미한다.
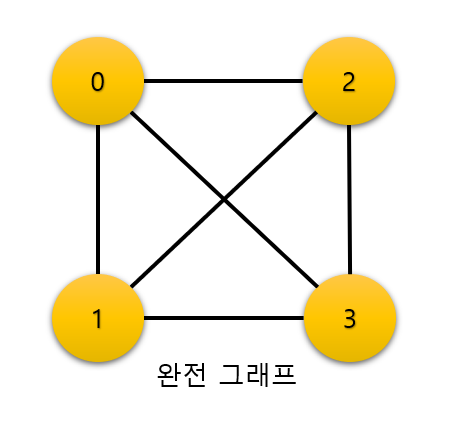
2. 완전 그래프
모든 정점이 서로 연결되어 있는 그래프를 완전 그래프라고 한다.
완전 그래프일 때 정점의 개수를 n이라고 하면 하나의 정점은 n-1개의 다른 정점과 연결되어
간선의 수는 n * (n-1) / 2 이다.
3. 가중치 그래프(weighted graph)
a에서 b로 가는 간선이 있다고 할때 이 간선을 지날때의 비용이나 가중치가 할당된 그래프를 가중치 그래프라고 한다.
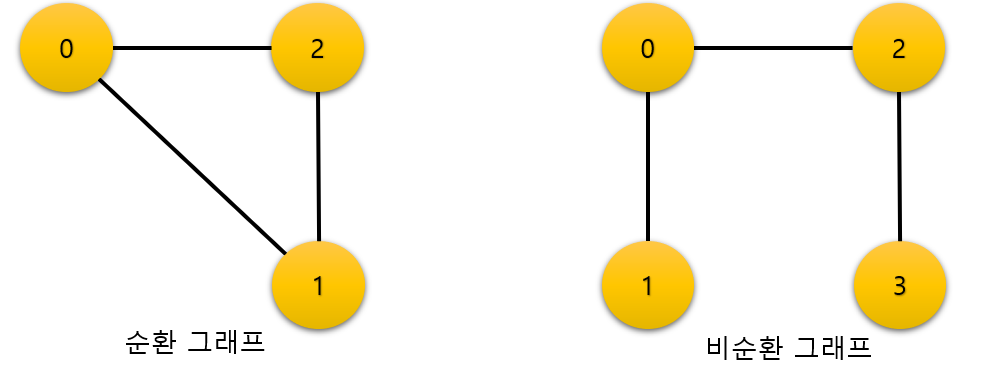
4. 순환(cycle), 비순환 그래프
순환 그래프는 사이클이 있는 그래프를 말하며 비순환 그래프는 사이클이 없는 그래프이다.
트리는 사이클이 없으므로 비순환적 그래프이다.
그래프 표현 방법
그래프를 표현하는 방법에는 2차원 배열을 이용한 인접 행렬 방법과 포인터를 이용한 인접 리스트 방법이 있다.
인접 행렬
정점의 수가 n개일 때 nxn 크기의 2차원 배열로 구현한 그래프이다.
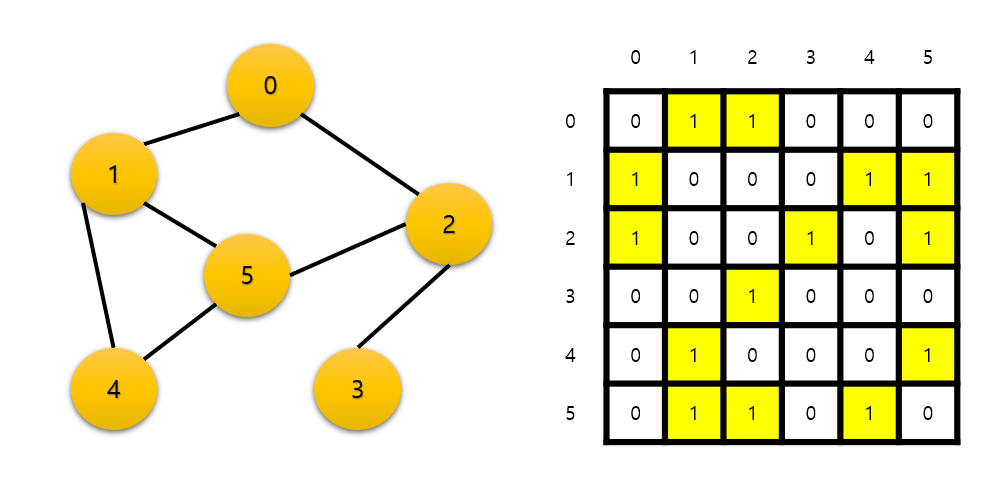
위 그림은 무방향 그래프를 인접 행렬로 나타낸 것이다.
인접 행렬을 배열 adj_mat 이라고 할 때 i에서 j로 가는 인접행렬은 adj_mat[i][j] 와 같이 표기한다.
인접 행렬에서 인접해 있을 때를 1, 아니면 0을 표기하고 가중치가 있는 경우는 가중치를 저장한다.
만약 0에서 1로가는 인접 행렬을 표현하자면 adj_mat[0][1] 이고 이 값은 1이다.
무방향 그래프는 0에서 1로 가는 경우와 1에서 0으로 가는 경우가 같으므로 대칭을 이룬다.
인접 행렬 특징
간선의 존재 여부를 확인하고자 할 때 인덱스를 통해 직접 접근 가능함으로 O(1)의 시간복잡도를 가진다.
모든 간선의 수를 파악하고자 하는 경우 전체 배열을 전부 탐색해봐야 함으로 O(n^2)의 시간복잡도를 가진다.
인접 리스트
정점의 수가 n개일 때 n개의 연결리스트의 포인터 배열을 만들어 구현한 그래프이다.
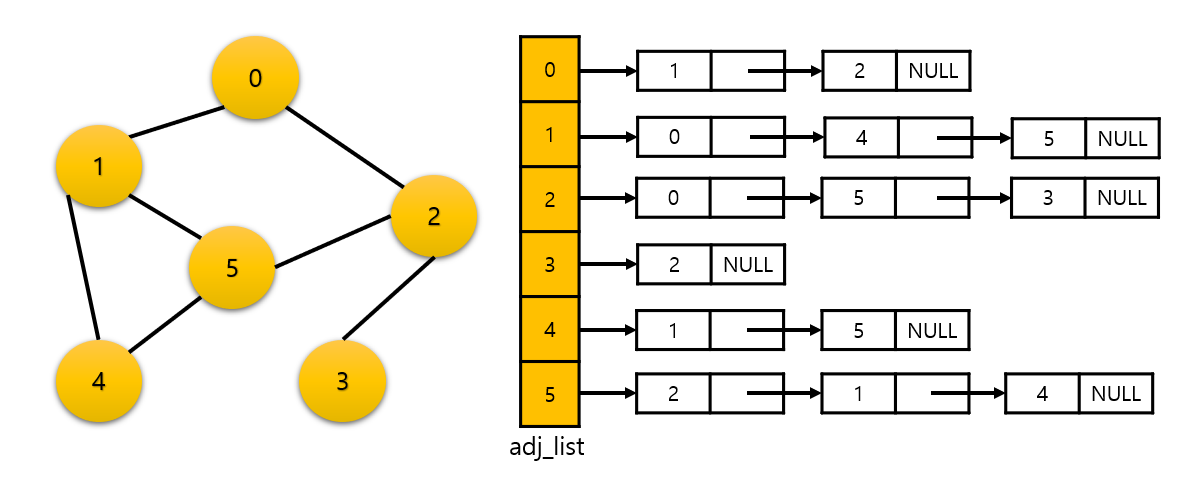
위 그림은 무방향 그래프를 인접 리스트로 나타낸 것이다.
인접 리스트는 포인터 배열로 각 정점과 연결된 노드를 가리킨다.
그래프 그림을 보면 2와 연결된 정점은 0, 5, 3 임을 알 수 있다. 이를 인접리스트의 2번 인덱스에 0, 5, 3을 가지는 노드를 연결리스트로 구현한다.
만약 가중치가 있는 그래프라면 노드에 정점과 가중치 값도 포함하게 된다.
인접 리스트 구현 및 특징
인접 리스트로 구현하면 인접 행렬은 모든 관계를 저장하여 노드의 개수가 많을 수록 메모리가 낭비되지만 인접리스트의 경우 관계를 정의 할때 연결된 정보만을 저장하여 메모리를 효율적으로 사용한다. 다만 인접 행렬 방식에서 특정 노드의 간선의 관계를 확인하기 위해 전부 확인 해야 한다는 점에서 인접 행렬은 바로 접근할 수 있는 데에 비해 비효율적이다.
인접 리스트에서 연결된 정점들의 순서는 기본적으로 어떤 순서이든 상관없다.
그래프 노드
정점과 정점을 연결 짓는 포인터 선언
typedef struct GraphNode
{
int vertex;
struct GraphNode *link;
} GraphNode;그래프 타입
정점의 개수와 인접 리스트의 선언
typedef struct GraphType
{
int n;
GraphNode *adj_list[MAX_VERTICES];
} GraphType;간선 삽입
u에서 v로 가는 간선을 삽입한다. 동적할당하여 노드를 만들고 넣고자하는 정점을 인접리스트가 가리키는 첫번째 요소에 삽입한다.
void insert_edge(GraphType *g, int u, int v)
{
GraphNode *node;
if (u >= g->n || v >= g->n)
{
printf("그래프 : 정점 번호 오류\n");
return;
}
node = (GraphNode *)malloc(sizeof(GraphNode));
node->vertex = v;
node->link = g->adj_list[u];
g->adj_list[u] = node;
}인접 리스트 전체 코드
#include <stdio.h>
#include <stdlib.h>
#define MAX_VERTICES 50
typedef struct GraphNode
{
int vertex;
struct GraphNode *link;
} GraphNode;
typedef struct GraphType
{
int n;
GraphNode *adj_list[MAX_VERTICES];
} GraphType;
// 그래프 초기화
void graph_init(GraphType *g)
{
int v;
g->n = 0;
for (v = 0; v < MAX_VERTICES; v++)
g->adj_list[v] = NULL;
}
// 정점 개수 확인
void insert_vertex(GraphType *g)
{
if ((g->n + 1) > MAX_VERTICES)
{
printf("그래프 : 정점의 개수 초과\n");
return;
}
g->n++;
}
// 간선 삽입
void insert_edge(GraphType *g, int u, int v)
{
GraphNode *node;
if (u >= g->n || v >= g->n)
{
printf("그래프 : 정점 번호 오류\n");
return;
}
node = (GraphNode *)malloc(sizeof(GraphNode));
node->vertex = v;
node->link = g->adj_list[u];
g->adj_list[u] = node;
}
void print_adj_list(GraphType *g)
{
for (int i = 0; i < g->n; i++)
{
GraphNode *p = g->adj_list[i];
printf("정점 %d의 인접 리스트 ", i);
while (p != NULL)
{
printf("-> %d ", p->vertex);
p = p->link;
}
printf("\n");
}
}
int main()
{
GraphType *g;
g = (GraphType *)malloc(sizeof(GraphType));
graph_init(g);
for (int i = 0; i < 6; i++)
insert_vertex(g);
insert_edge(g, 0, 2);
insert_edge(g, 0, 1);
insert_edge(g, 1, 5);
insert_edge(g, 1, 4);
insert_edge(g, 1, 0);
insert_edge(g, 2, 3);
insert_edge(g, 2, 5);
insert_edge(g, 2, 0);
insert_edge(g, 3, 2);
insert_edge(g, 4, 5);
insert_edge(g, 4, 1);
insert_edge(g, 5, 4);
insert_edge(g, 5, 1);
insert_edge(g, 5, 2);
print_adj_list(g);
free(g);
return 0;
}결과
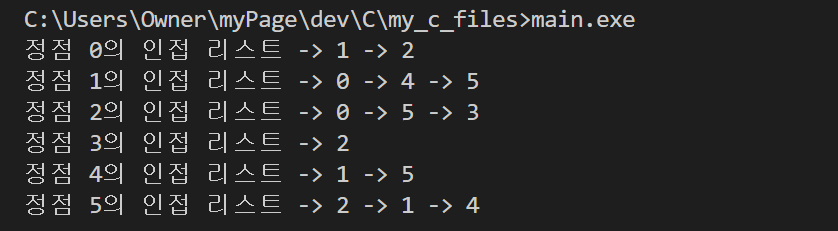
마무리
그래프의 개념과 이를 구현하는 방법인 인접 행렬, 인접 리스트에 알아보고 간단한 코드도 구현해보았다.
그래프는 비선형 자료구조로 이후 배울 dfs, bfs 와 같은 탐색 알고리즘 같이 여러 방면에서 자주 사용되는 자료구조임으로 개념과 용어를 잘 알아두자!
📕 참고 문헌
다음의 책을 참고했습니다.
C언어로 쉽게 풀어쓴 자료구조 [ 개정3판 ]
천인국, 공용해, 하상호 저 | 생능출판사 | 2021년 08월 20일