이진 탐색 트리

앞선 글에서는 트리와 이진트리에 대해 설명하였다. 이진 탐색트리는 이진 트리로 만들어진 탐색을 위한 자료구조이다.
이번에는 이진 탐색 트리에 대해 알아보자.

정의

이진탐색트리는 BinarySearchTree로 줄여서 BST라고도 부른다. 이진트리와 다른 이진탐색트리만의 특징이 있는데 다음과 같이 정의된다.

- 왼쪽 서브 트리의 값은 루트 값보다 작다.

- 오른쪽 서브 트리의 값은 루트 값보다 크다.

- 왼쪽 서브트리 오른쪽 서브트리도 이진 탐색트리를 만족한다.

- 중복이 되는 값은 존재하지 않는다.

이러한 특징 때문에 루트를 기준으로 왼쪽 서브트리의 값들은 루트보다 작고 오른쪽 서브트리의 값들은 루트보다 크다.

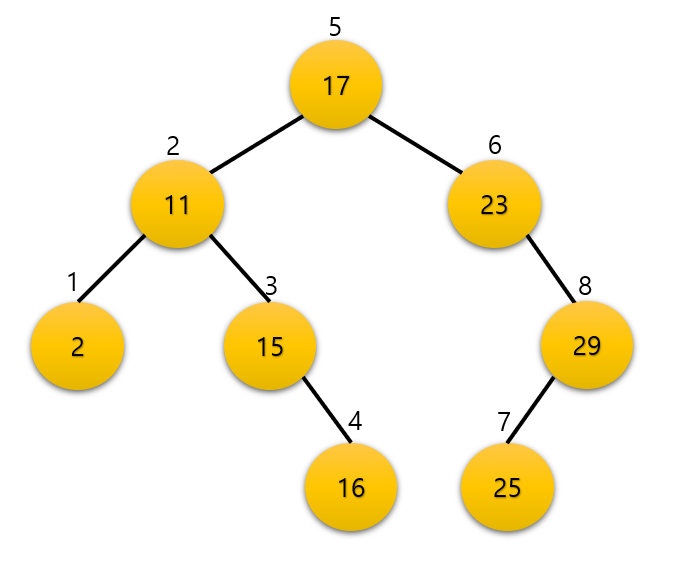
위 이미지는 이진 탐색 트리에 중위 순회한 순서를 적어둔 것이다. 순서를 따라 값을 적어보면 { 2, 11, 15, 16, 17, 23, 25, 29 } 라는 값이 나열된다. 숫자들의 순서를 보면 오름차순으로 나열되어 있는 것을 확인할 수 있다. 즉, 이진 탐색 트리에서 중위순회를 하면 정렬된 값을 얻을 수 있다.

이진 탐색 트리의 연산 및 구현

이진 탐색 트리에서 값은 키(key)라고 하고 왼쪽 서브트리는 left 오른쪽 서브트리는 right로 표기한다.

탐색(Search) 연산

먼저 루트부터 시작해서 루트와 값을 비교후 값이 작으면 왼쪽 서브 트리로 이동, 값이 크면 오른쪽 서브 트리로 이동하여 같은 값이 나올 때까지 탐색을 시도한다.

탐색을 성공하면 해당 노드를 반환하고 탐색을 실패할 경우 NULL을 반환한다.

순환을 이용한 탐색

다음은 재귀함수를 사용하여 이진 탐색 트리의 탐색을 구현한 코드이다.

TreeNode *recursive_search(TreeNode *node, element key)
{
    if (node == NULL)
        return NULL;
    if (key == node->key)
        return node;
    else if (key < node->key)
        return recursive_search(node->left, key);
    else
        return recursive_search(node->right, key);
}

반복을 이용한 탐색

반복문을 사용하여 이진 탐색 트리의 탐색을 구현한 코드이다. node 값이 변경되어도 복사된 포인터변수를 사용하는 것이기 때문에 실제 node의 값은 변경 되지 않는다.

TreeNode *loop_search(TreeNode *node, element key)
{
    while (node != NULL)
    {
        if (key == node->key)
            return node;
        if (key < node->key)
            node = node->left;
        else
            node = node->right;
    }

    return NULL;
}

삽입(Insert) 연산

이진 탐색 트리는 앞서 보았던 탐색 연산과 비슷하게 수행된다. 넣고자 하는 값을 key라고 할때 key와 현재 노드의 값을 비교하여 위치를 조정한다.

키 값이 노드의 값보다 작으면 왼쪽 서브트리로 이동, 키 값이 노드의 값보다 크면 오른쪽 서브트리로 이동하고 맨 마지막에 NULL 값이 오는 곳이 해당 key가 삽입될 위치가 된다.

만약 탐색 도중 같은 값이 나오면 오류가 생기므로 종료한다.

TreeNode *new_node(element item)
{
    TreeNode *node = (TreeNode *)malloc(sizeof(TreeNode));
    node->key = item;
    node->left = node->right = NULL;
    return node;
}

TreeNode *insert_node(TreeNode *node, element key)
{
    if (node == NULL) // 새로 노드를 생성해 삽입한다.
        return new_node(key);
    if (key < node->key)
        node->left = insert_node(node->left, key);
    else if (key > node->key)
        node->right = insert_node(node->right, key);
    else
        fprintf(stderr, "트리에 중복된 값이 있습니다.\n");

    return node;
}

삭제(Delete) 연산

이진 탐색 트리의 연산 중 삭제 연산이 가장 복잡하다.

한번 생각을 해보자 이진 탐색 트리의 맨 마지막 노드를 삭제하는 것은 간단할 것이다.
그러나 만약 중간에 있는 노드를 삭제하고자 한다면?

중간에 있는 노드가 연결된 서브 트리와 루트 노드 간에 구멍이 생길 것이다.
따라서 중간에 있는 노드의 위치에 서브 트리를 연결 시키는 것이 중요하다.

특히 서브트리의 값을 연결 시키고자 할 때 삭제된 노드와 가장 값의 차이가 작은 노드를 선택해야 한다.

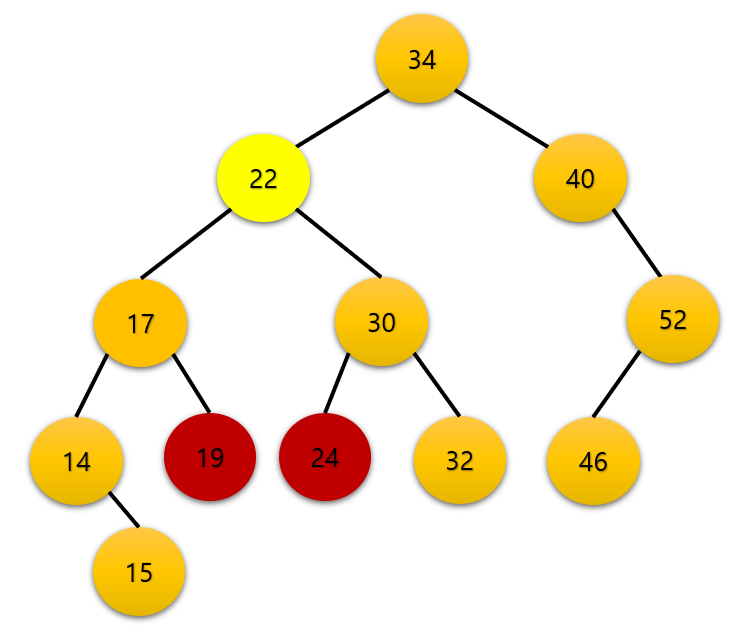
위 이미지에서 22를 삭제 한다고 생각해보자. 자식 노드인 30이 22에 있는 위치에 들어가면 이진 탐색 트리의 조건을 만족하지 못 할 것이다. 따라서 왼쪽 서브 트리에서 가장 큰 노드인 19와 오른쪽 서브트리에서 가장 작은 노드인 24 중에서 하나를 택하여 연결하면 된다. 왼쪽 서브트리의 가장 큰 노드는 오른쪽으로 계속 이동하고 오른쪽 서브트리의 가장 작은 노드는 왼쪽으로 계속 이동하여 값을 얻을 수 있다.

해당 코드에서는 오른쪽 서브트리의 가장 작은 값을 얻어 연결하도록 하였다.

TreeNode *get_min_subtree(TreeNode *node)
{
    while (node->left != NULL)
        node = node->left;
    return node;
}

TreeNode *delete_node(TreeNode *node, element key)
{
    if (node == NULL)
        return node;
    // 삭제하고자 하는 노드를 찾을 때까지 탐색을 수행한다.
    if (key < node->key)
        node->left = delete_node(node->left, key);
    else if (key > node->key)
        node->right = delete_node(node->right, key);
    else
    { // 삭제하고자 하는 값을 찾았을 때
        // 자식 노드가 하나 또는 없는 경우
        if (node->left == NULL)
        {
            TreeNode *linked_node = node->right;
            free(node);
            return linked_node;
        }
        else if (node->right == NULL)
        {
            TreeNode *linked_node = node->left;
            free(node);
            return linked_node;
        }
        // 자식노드가 두개인 경우
        TreeNode *linked_node = get_min_subtree(node->right);     // 오른쪽 서브트리 최대값
        node->key = linked_node->key;                             // 오른쪽 서브트리 최대값을 삭제하고자 하는 노드에 복사
        node->right = delete_node(node->right, linked_node->key); // 오른쪽 서브트리 최대값 삭제
    }
}

전체 코드

#include <stdio.h>
#include <stdlib.h>

typedef int element;
typedef struct TreeNode
{
    element key;
    struct TreeNode *left, *right;
} TreeNode;

TreeNode *recursive_search(TreeNode *node, element key)
{
    if (node == NULL)
        return NULL;
    if (key == node->key)
        return node;
    else if (key < node->key)
        return recursive_search(node->left, key);
    else
        return recursive_search(node->right, key);
}

TreeNode *loop_search(TreeNode *node, element key)
{
    while (node != NULL)
    {
        if (key == node->key)
            return node;
        if (key < node->key)
            node = node->left;
        else
            node = node->right;
    }

    return NULL;
}

TreeNode *new_node(element item)
{
    TreeNode *node = (TreeNode *)malloc(sizeof(TreeNode));
    node->key = item;
    node->left = node->right = NULL;
    return node;
}

TreeNode *insert_node(TreeNode *node, element key)
{
    if (node == NULL)
        return new_node(key);
    if (key < node->key)
        node->left = insert_node(node->left, key);
    else if (key > node->key)
        node->right = insert_node(node->right, key);
    else
        fprintf(stderr, "트리에 중복된 값이 있습니다.\n");

    return node;
}

TreeNode *get_min_subtree(TreeNode *node)
{
    while (node->left != NULL)
        node = node->left;
    return node;
}

TreeNode *delete_node(TreeNode *node, element key)
{
    if (node == NULL)
        return node;
    // 삭제하고자 하는 노드를 찾을 때까지 탐색을 수행한다.
    if (key < node->key)
        node->left = delete_node(node->left, key);
    else if (key > node->key)
        node->right = delete_node(node->right, key);
    else
    { // 삭제하고자 하는 값을 찾았을 때
        // 자식 노드가 하나 또는 없는 경우
        if (node->left == NULL)
        {
            TreeNode *linked_node = node->right;
            free(node);
            return linked_node;
        }
        else if (node->right == NULL)
        {
            TreeNode *linked_node = node->left;
            free(node);
            return linked_node;
        }
        // 자식노드가 두개인 경우
        TreeNode *linked_node = get_min_subtree(node->right);     // 오른쪽 서브트리 최대값
        node->key = linked_node->key;                             // 오른쪽 서브트리 초대값을 삭제하고자 하는 노드에 복사
        node->right = delete_node(node->right, linked_node->key); // 오른쪽 서브트리 최대값 삭제
    }
}

void inorder(TreeNode *root)
{
    if (root != NULL)
    {
        inorder(root->left);
        printf("%d ", root->key);
        inorder(root->right);
    }
}

int main(void)
{
    TreeNode *root = NULL;

    root = insert_node(root, 30);
    root = insert_node(root, 20);
    root = insert_node(root, 25);
    root = insert_node(root, 10);
    root = insert_node(root, 50);
    root = insert_node(root, 70);
    delete_node(root, 30);

    printf("중위 순회를 이용한 정렬\n");
    inorder(root);

    return 0;
}

이진 탐색 트리 복잡도

이진 탐색 트리에서 탐색, 삽입, 삭제의 경우 탐색 범위가 트리의 높이에 영향을 받으므로 트리의 높이가 h일 때 O(h) 값을 가진다.

이상적인 조건인 완전 이진트리의 형태를 가진 이진 탐색트리의 경우 n개의 노드를 가진다고 했을 때 n/2 씩 탐색 범위가 줄어들어 O($\log_2 n$)의 값을 가지고 최악의 경우인 경사 이진 트리의 경우 O(n)의 값을 가진다.

최악의 경우 기존의 선형 탐색과 동일한 연산을 수행한다. 만약 노드의 개수에 비해 트리의 높이가 높게 유지된다면 탐색에서 손해를 볼 것이다.

이를 해결하기 위해 고안된 방법이 AVL트리가 있다. 트리의 높이를 항상 ⌈$\log_2 n$⌉ 으로 유지시키는 방법으로 해당 자료구조를 사용하면 효율적인 탐색을 할 수 있다.

📕 참고 문헌

다음의 책을 참고했습니다.
C언어로 쉽게 풀어쓴 자료구조 [ 개정3판 ]
천인국, 공용해, 하상호 저 | 생능출판사 | 2021년 08월 20일