트리란?

트리는 우리가 아는 트리 형태의 구조를 가진 자료구조를 말한다. 그간 리스트, 스택, 큐와 같은 선형 자료구조에 대해서 공부했는데 트리의 경우 비선형 자료구조로 계층적인 구조를 가지고 있다.

선형 자료구조: 자료들이 선형으로 나열되어 있는 구조로 앞, 뒤 관계가 1:1의 관계를 가짐.

비선형 자료구조: 하나의 자료 뒤에 여러 개의 자료가 존재할 수 있는 구조로 앞, 뒤 관계가 1:n 또는 n:n의 관계를 가짐.

트리의 예시로는 가족의 가계도, 회사의 조직도, 컴퓨터의 디렉토리 구조 등이 있다.

트리의 용어

트리는 부모-자식 간의 관계의 노드들로 이루어져있다. 트리에서 사용되는 용어를 정리해보자.

노드(node): 트리의 구성 요소
간선(edge): 노드를 연결하는 선
루트(root): 부모가 없는 노드
서브트리(subtree): 하나의 노드와 그 노드들의 자손들로 이루어진 트리
단말 노드(terminal node, leaf node): 자식이 없는 노드(맨 끝에 있는 노드)
비단말 노드(non-terminal node): 적어도 하나의 자식을 가지는 노드
레벨(level): 트리의 각 층의 번호(1레벨부터 시작)
높이(height): 트리의 최대 레벨(깊이를 말함)
차수(degree): 노드가 가지고 있는 자식 노드의 개수(트리의 차수는 트리의 최대 차수를 가리키는 말임)
부모 노드(parent node): 임의의 노드 바로 위의 노드
자식 노드(children node): 부모 노드 바로 아래의 노드
형제 노드(sibling node: 같은 부모를 가지는 노드
조상 노드(ancestor node): 임의의 노드 위부터 경로를 따라 루트 노드까지 해당하는 노드
후손 노드(descendent node): 어떤 노드의 서브 트리에 속하는 모든 노드
포리스트(forest): 트리들의 집합

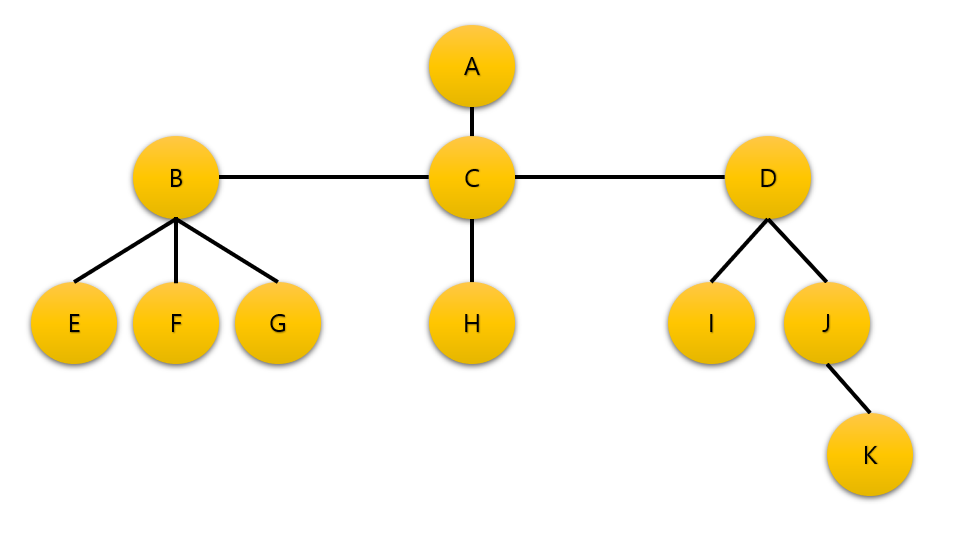
트리의 구조

위의 사진을 보면서 트리의 용어와 쓰임에 대해 더 자세히 알아보자.

루트 노드는 A이다.
B, C, D는 형제 노드이다.
C는 H의 부모 노드이다.
H는 C의 자식 노드이다.
E, F, G는 단말 노드이다.
트리의 높이는 4이다.
D의 차수는 2이다.

이진트리(binary tree)

지금까지 트리의 개념과 용어에 대해 알아보았다. 트리는 자식 노드의 개수에 따라 형태가 변한다. 그중 자식 노드의 개수가 2개 이하인 트리를 이진트리라고 한다. 트리 중에서 가장 활용도가 높은 트리임으로 잘 알아두자.

• 이진트리는 모든 차수가 2이하인 값을 가지고 트리를 말한다. 이는 자식 노드의 개수가 2개 이하임을 의미한다.

특징

• 서브 트리간의 순서가 존재한다. 서브트리를 왼쪽 서브트리, 오른쪽 서브트리로 구분시켜 사용한다.

• 모든 자식 노드는 부모 노드와 간선을 1개씩만 가진다. 루트 노드를 제외한 자식 노드의 개수가 간선의 개수이다. ⇒ 노드의 개수: n, 간선의 개수: n-1

• 높이가 h인 이진트리의 경우 최소 h개의 노드, 최대 2^h-1개의 노드를 가진다.

• n개의 노드를 가지는 경우 이진트리의 높이는 최소 천정 ⌈log2(n+1)⌉ , 최대 n ⇒ 최소인 경우 완전 이진트리를 만족할 때 최소이다.

이진 트리의 종류

포화 이진트리

• 각 레벨에 노드가 꽉차있는 노드를 의미.

완전 이진트리

• 높이를 h라고 하면 h-1까지 노드가 꽉 차있고 h번째부터는 왼쪽부터 오른쪽까지 순서대로 차있는 트리를 말한다. 포화 이진 트리와 다르게 h번째는 꽉 있지 않을 수 있다.

기타 이진트리

• 포화, 완전 이진트리를 제외한 이진트리를 말한다.

구현

이진 트리를 구현하는 방법에는 2가지가 존재한다.

• 배열을 사용해 구현하는 방법
• 포인터를 사용해 연결된 트리를 구현하는 방법

배열로 구현한 이진트리

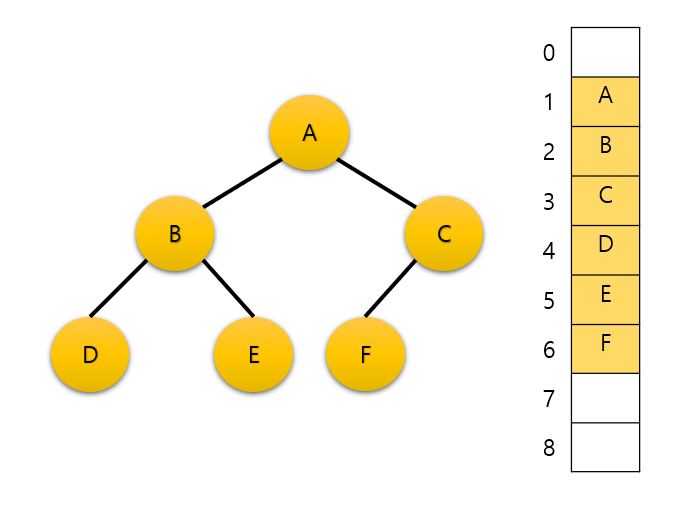
배열의 경우 위 사진과 같이 인덱스 1번부터 레벨 순, 왼쪽부터 오른쪽 순으로 순서대로 배열에 인덱스에 저장 할 수 있다.

i를 특정 노드의 인덱스라고 할 때 부모의 인덱스, 자식 노드의 인덱스에 접근할 수 있다.

노드 i의 부모 노드 인덱스 = i / 2
노드 i의 왼쪽 자식 노드 인덱스 = 2 * i
노드 i의 오른쪽 자식 노드 인덱스 = 2 * i + 1

만약 위 사진에서 C의 인덱스인 3을 알고 있다고 했을 때 부모 노드인 A의 인덱스는 3에서 2를 나눈 몫인 1의 값을 가진다. 왼쪽 자식 노드의 경우 3 * 2인 6의 인덱스를 가진다.

해당 방법은 구현하기 간단하다는 장점이 있지만 만약 경사 이진 트리와 같이 완전 이진 트리가 아닌 경우에는 배열에 빈 공간이 많이 메모리 측면에서 비효율적이다.

포인터로 구현한 이진트리

포인터를 사용해 부모 노드와 자식 노드간의 간선을 연결한다. 트리의 개념을 잘 적용한 방법이라고 볼 수 있다. 하나의 노드에는 자료를 담는 데이터와 왼쪽 노드를 연결하는 포인터, 오른쪽 노드를 연결하는 포인터가 있다.

구조체 노드 구현

typedef struct TreeNode {
	int data;
    struct TreeNode *left, *right;
} TreeNode;

트리의 순회

루트 노드를 알면 트리의 모든 노드에 접근 할 수 있다. 이를 사용하여 전위, 중위, 후위 순회를 할 수 있다.

트리의 순회를 결정하는 방식에는 3가지가 존재한다.
1. 왼쪽 서브트리 방문 : L(left)
2. 루트 방문 : V(Visit)
3. 오른쪽 서브트리 방문 : R(Right)

위 세가지 방식에 따라 루트 방문 V를 기점으로 순회방식이 3가지로 나눈다.
순회를 하기 위해 순환 기법을 사용하여 다음 노드 방문을 결정한다.

전위순회: VLR(preorder traversal)

순서

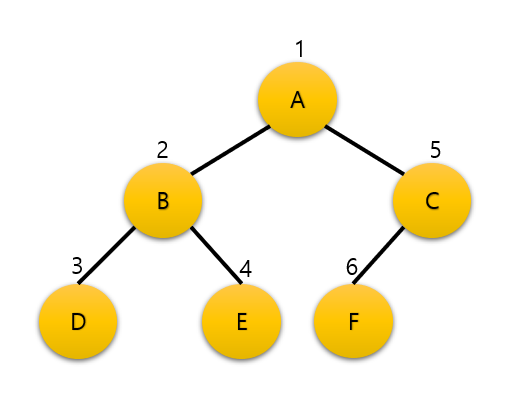
구현

void preorder(TreeNode *p){
	if(p != NULL){
		printf("[ %d ] ", p->data);
		preorder(p->left);
		preorder(p->right);
	}
}

중위순회: LVR(inorder traversal)

순서

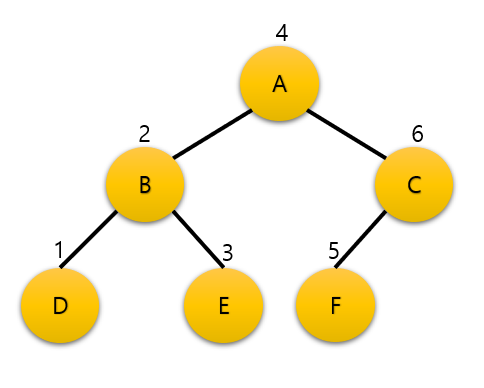
구현

void inorder(TreeNode *p){
	if(p != NULL){
    	inorder(p->left);
        printf("[ %d ] ", p->data);
        inorder(p->right);
    }
}

후위순회: LRV(postorder traversal)

순서

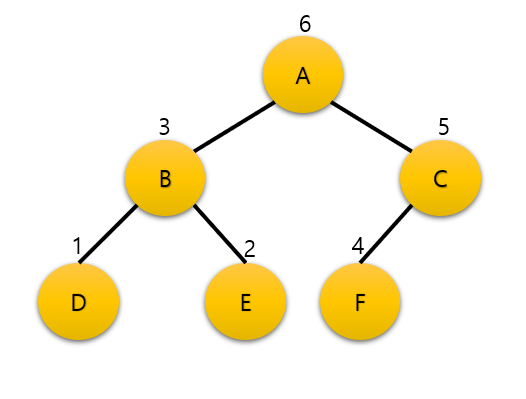
구현

void postorder(TreeNode *p){
	if(p != NULL){
    	postorder(p->left);
        postorder(p->right);
        printf("[ %d ] ", p->data);
    }
}

마무리

비선형 자료구조 중 하나인 트리의 개념과 용어에 대해 간단히 알아보고 이진트리도 구현해 보았다. 특히 이진트리는 탐색과 같은 작업에도 많이 사용함으로 기본 개념을 잘 알아두자.

📕 참고 문헌

다음의 책을 참고했습니다.
C언어로 쉽게 풀어쓴 자료구조 [ 개정3판 ]
천인국, 공용해, 하상호 저 | 생능출판사 | 2021년 08월 20일