🤔 Thinking
첫번째 풀이
전체 경로에 따른 최단경로를 구하기 위해서 전체 가능한 경로를 전부 찾으면 풀 수 있다고 생각하여 dfs를 이용해 작성하였다.
💻 DFS 로 짠 코드
def out_maps(x, y, maps):
return (-1 < x < len(maps)) and (-1 < y < len(maps[0])) # 맵을 벗어난 경우
def dfs_mat(maps, move_to, v, move):
x, y = v
if x == len(maps)-1 and y == len(maps[0])-1: # 상대팀 진영에 도착한 경우
global answer
answer = min(answer, move)
return
for mx, my in move_to:
if (out_maps(x+mx, y+my, maps) and maps[x+mx][y+my]): # 맵에 장애물이 없는 지 확인
maps[x+mx][y+my] = 0
dfs_mat(maps, move_to, (x+mx, y+my), move+1) # 이동
maps[x+mx][y+my] = 1 # 이전 상태 복구
def solution(maps):
global answer
max_size = 100 * 100 + 1
answer = max_size
move_to = [(1, 0), (-1, -0), (0, -1), (0, 1)]
dfs_mat(maps, move_to, (0,0), 1)
return -1 if (max_size == answer) else answer나의 실수
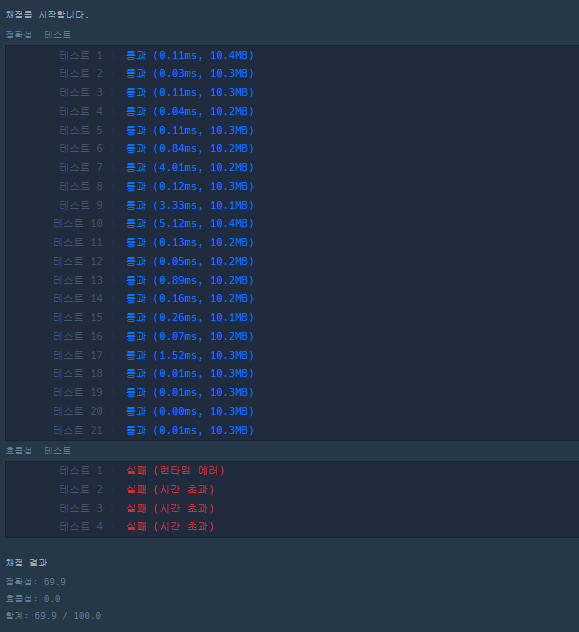
테스트를 돌려보니 효율성 테스트에서 전부 시간초과가 나왔다.
dfs에서는 백트레킹(?) 처럼 방문 후 다시 돌아왔을 때 이전상태로 바꿔주어야한다.
maps[x+mx][y+my] = 0
dfs_mat(maps, move_to, (x+mx, y+my), move+1) # 이동
maps[x+mx][y+my] = 1 # 이전 상태 복구dfs를 사용하면 이동시 매번 가능한 전체 경로를 탐색하기 때문에 매우 많은 경우의 수를 탐색해야 한다. 최단 거리가 아닌 경우도 탐색한다.
🙆♂️ 정답 풀이
두번째 풀이
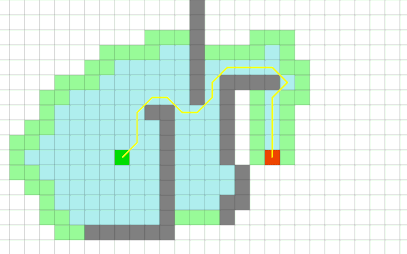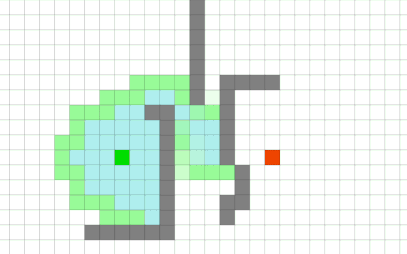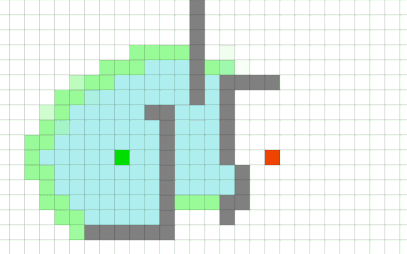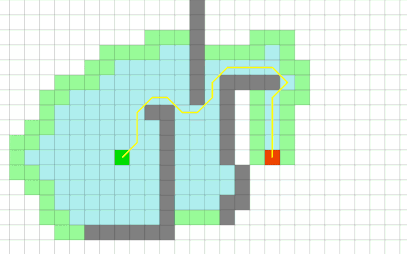
BFS 에서는 최단 거리를 구할 때 조건을 만족하면 종료하기 때문에 전체 경로를 탐색하는 dfs의 방식 보다 더 빠르다.
BFS와 DFS의 차이점을 실제 문제로 깨닫게 해주는 문제였다.
💻 BFS 로 짠 코드
BFS에서는 현재 이동거리를 큐에 인덱스와 같이 저장하였다.
from collections import deque
def out_maps(x, y, maps):
return (-1 < x < len(maps)) and (-1 < y < len(maps[0]))
def bfs_mat(maps, v):
queue = deque([v])
move_to = [(1, 0), (-1, -0), (0, -1), (0, 1)]
max_size = 100 * 100 + 1
result = max_size
while(queue):
x, y, move = queue.popleft()
for mx, my in move_to:
if (out_maps(x+mx, y+my, maps) and maps[x+mx][y+my]):
queue.append((x+mx, y+my, move+1))
maps[x+mx][y+my] = 0 # 방문
if x == len(maps)-1 and y == len(maps[0])-1:
result = min(result, move)
return -1 if result == max_size else result
def solution(maps):
answer = bfs_mat(maps, (0,0,1))
return answer
