[프로그래머스] 타겟넘버 - 43165

문제링크

DFS/BFS 문제 중 2차원 배열이 아닌 노드간의 그래프 형식의 문제의 경우에도 DFS/BFS 문제임을 알게 되어서 기록한다.

🤔 Thinking

나의 접근

처음에 음수인 경우와 양수인 경우를 각각 노드마다 정한 후 모든 경우의 수를 파악해야 한다고 생각하였다.
재귀 함수를 이용해서 아래와 같이 전부 비교하면 될 것이라고 생각하였다.

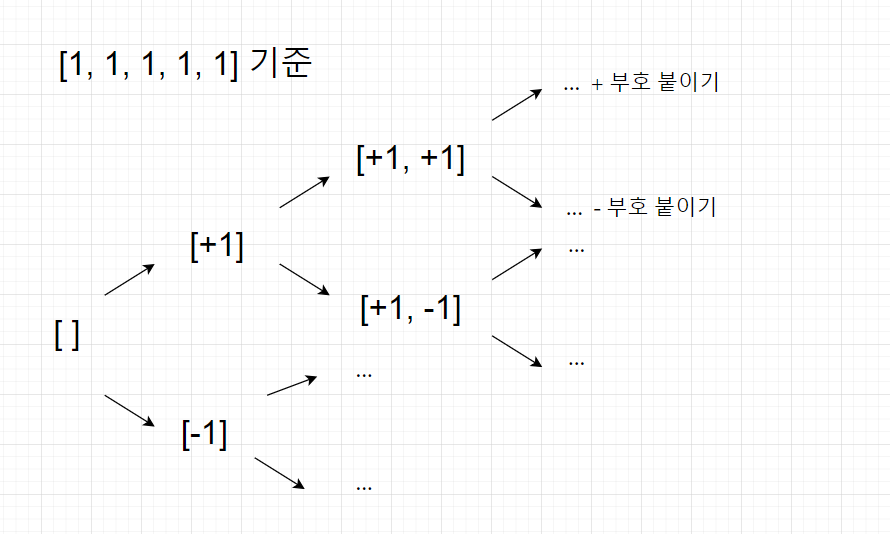
[  1  1  1  1  1  ] 기준
1. [  1  1  1  1  1  ]
2. [ -1  1  1  1  1  ]
3. [  1 -1  1  1  1  ]

...

n-1.[  1 -1 -1 -1 -1  ]
n.  [ -1 -1 -1 -1 -1  ]

다만, 코드를 작성해서 구현하는 것은 쉽게 떠오르지 않았다.

💡 아이디어

0부터 n-1 번까지 다음 인덱스의 number 에 (+) 또는 (-) 부호 를 붙여 각 숫자에서 2가지 경우의 수를 만든다. 이렇게 모든 경우의 수를 확인 할 수 있다.

기존의 방식은 2차원 배열의 그래프를 이용한 dfs/bfs 문제를 봐왔는데 이렇게 직접 경우의 수를 만들어 그래프 형태로 풀 수 있음을 알게되었다.

💻 Code

각각의 인덱스 값을 알아야 다음 number를 추가할 수 있기 때문에 인덱스도 같이 매개변수로 넘겨 준다.

DFS로 푼 코드

def dfs(numbers, target, v, idx):
    global answer
    
    if idx == len(numbers): # n 번째인 경우 종료
        if v == target:		# 조건 만족시 카운트
            answer += 1
        return
    dfs(numbers, target, v+numbers[idx], idx+1) # + 부호 붙이기
    dfs(numbers, target, v-numbers[idx], idx+1) # - 부호 붙이기
    
def solution(numbers, target):
    global answer
    answer = 0
    
    dfs(numbers, target, 0, 0)
    
    return answer

BFS로 푼 코드

from collections import deque

def bfs(numbers, target, vertex, index):
    result = 0
    queue = deque([(vertex, index)]) # 큐 사용
    
    while queue:
        v, idx = queue.popleft()
    
        if idx == len(numbers):
            if v == target:
                result += 1
        else:
            queue.append((v+numbers[idx], idx+1)) # + 부호 붙이기
            queue.append((v-numbers[idx], idx+1)) # - 부호 붙이기
        
    return result
    
def solution(numbers, target):
    answer = bfs(numbers, target, 0, 0)
    
    return answer