[컴퓨터비전 STUDY / KOCW 한동대학교 황성수 교수님 강의 Review]
Line
Hough tranform 알고리즘을 사용해서 선(line)을 검출한다.
What is Hough transform?
이미지 상의 특정한 점들 간의 연관성을 찾아 특징을 추출하는 방법
(Lane Detection)에서 많이 활용된다.
-
y = ax + b 를 b = -ax + y 로 변환한다.
(xy 평면 상에서 기울기와 y절편의 평면인 ab 평면으로 옮긴다.) -
각각의 edge pixel 로부터 모든 조합의 (a, b)를 찾는다.
-
여러 번 사용되는 (a, b)의 조합은 입력 영상의 선이 된다.
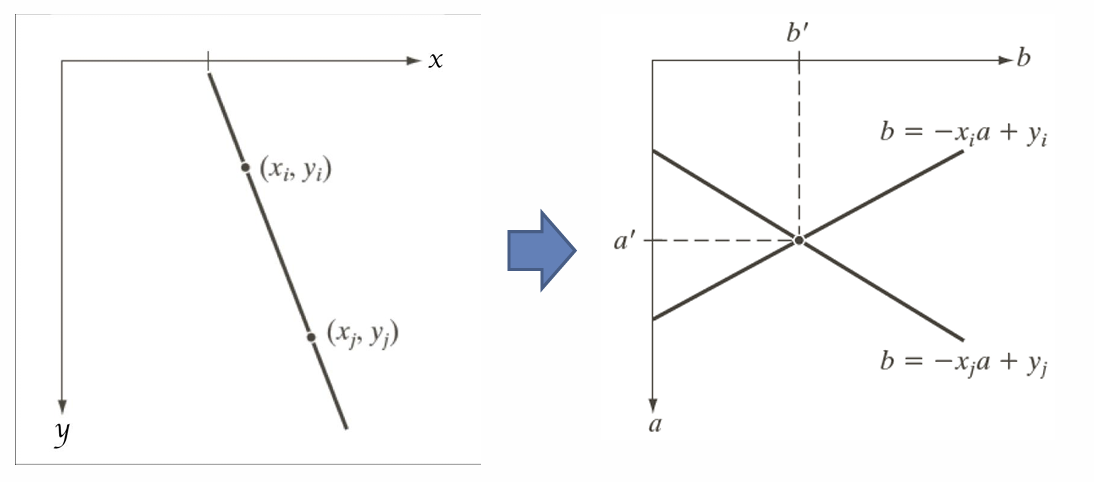
결국, ab평면 상에서의 직선을 구하고 그 직선들간의 교점의 존재 여부를 확인해 보면 같은 직선 상의 점인지 아닌지를 알 수 있다.
하지만, 위의 방법은 한가지 문제점이 있다.
만약 기울기가 0일 경우, 무수히 많은 직선이 형성되어 각 점들 간의 연관성을 찾을 수 없게 되는 것이다.
따라서 실제 Hough transform은 기울기와 y절편의 평면이 아닌 이산적으로 계산할 수 있는 극좌표계, rθ평면으로 변환한다.
오른쪽 그림은 변환한 후의 그래프이다.
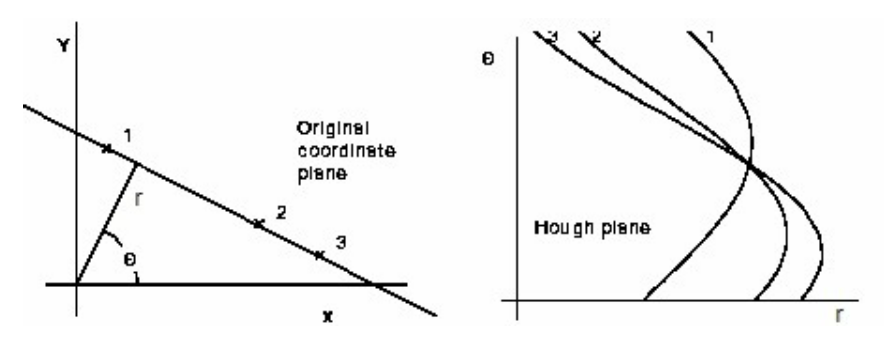
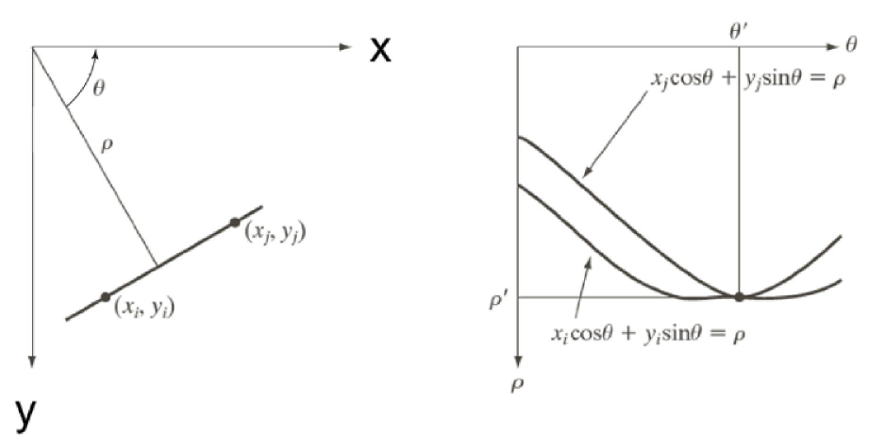
xy평면 상의 직선을 r과 θ에 대한 표현으로 바꿀 수 있다.
원점에서부터 직선까지의 거리를 r, x 축과의 기울기를 θ라고 하면, 다음의 수식들을 이용해 변환할 수 있다.
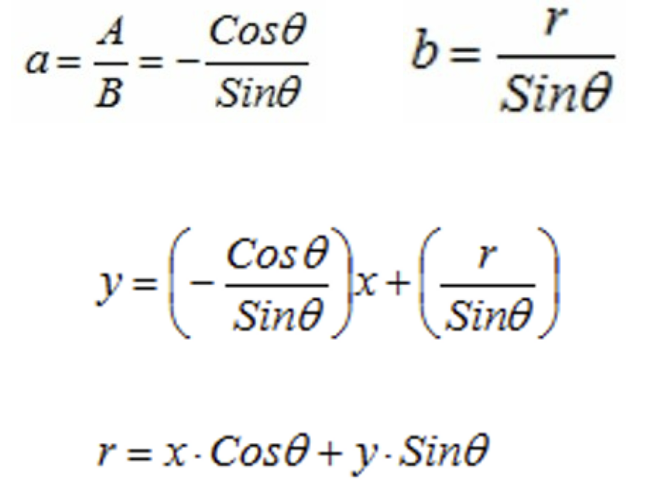
Hough Transform
알고리즘은 다음과 같다.
-
binary edge 이미지를 얻는다.
-
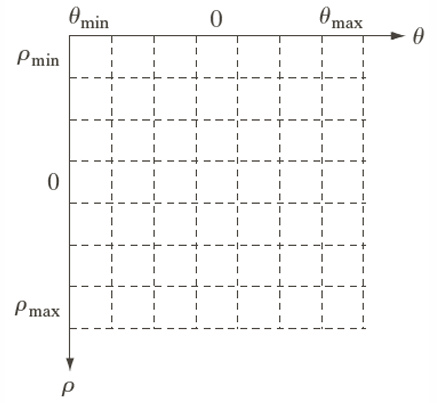
𝜌𝜃 − plane에서 세부 항목을 지정한다.
-
높은 픽셀 집중에 대해 accumulator 셀의 수를 검사한다.
(accumulator는 아래 그림과 같다.) -
선택한 셀의 픽셀 간의 관계(연결성)를 조사한다.
Circle detection
Hough Transform을 이용해 원을 검출할 수도 있다.
변환은 g(v, c)=0 형태의 모든 함수에 적용 가능하다.
여기서 v는 좌표 벡터이고 c는 계수 벡터이다.
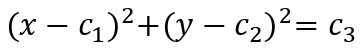
위 원의 방정식은 c1, c2, c3 3개의 파라미터를 가지고 있으므로, Hough transform을 그대로 사용하려면, c1, c2, c3의 3차원 파라미터 공간으로 변환시켜야 한다.
여기서 <x, y>를 상수로, <c1, c2, c3>를 변수로 판단하면 식은 다음과 같이 바뀐다.
(a, b, r은 차례대로 c1, c2, c3 이다.)
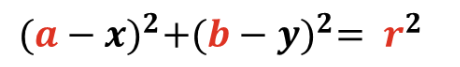
r(c3)에 상수를 하나씩 대입시키면서 생각해 보면, 아래 그림과 같이 xy 공간에서 원 위의 한 점은 a, b, r의 3차원 파라미터 공간에서 원뿔의 표면으로 표현된다.
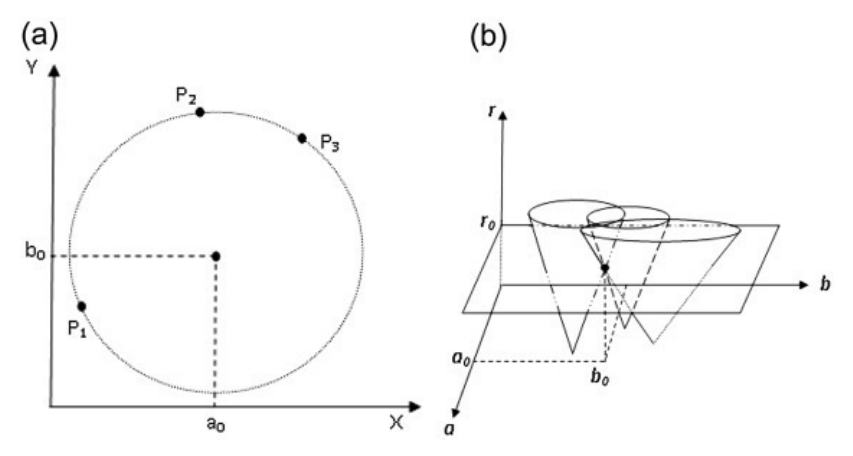
영상의 Edge 픽셀들을 Hough Transform 시켜 만들어진, 원뿔들의 표면이 많이 교차하는 점을 찾으면 원을 검출할 수 있다.
다음은 Houghlines(표준 허프 변환)을 사용하여 이미지에서 직선을 검출하는 과정을 구현하는 코드이다.
int main() {
Mat image, edge, result;
float rho, theta, a, b, x0, y0;
Point p1, p2;
vector<Vec2f> lines;
image = imread("chess_pattern.png"); // 이미지 파일 로드
result = image.clone(); // 이미지 복사본을 result 변수에 저장하여 후처리 과정에서 사용함
cvtColor(image, image, CV_BGR2GRAY); // 이미지를 grayscale로 변환함
# 두 개의 임계값 (50, 200)과 소벨 커널의 크기(3)를 사용하여 Edge를 검출함
Canny(image, edge, 50, 200, 3); // canny 함수를 사용하여 이미지의 엣지를 검출함
//applying Hough Transform to find lines in the image
//edge: input Mat, lines: output vector of lines
//1: (rho) distance resolution of the accumulator in pixels (거리 해상도)
//CV_PI/180: (theta) angle resolution of the accumulator in radians (각도 해상도)
//150: (threshold) accumulator threshold parameter (직선 검출 임계값)
// Edge 이미지에서 직선을 검출함
// 검출된 직선은 lines 벡터에 저장됨
HoughLines(edge, lines, 1, CV_PI / 180, 150);
for (int i = 0; i < lines.size(); i++) {
rho = lines[i][0]; // 원점에서 직선까지의 거리
theta = lines[i][1]; // 직선의 방향을 나타내는 각도
a = cos(theta); // 직선의 x 방향 성분
b = sin(theta); // 직선의 y 방향 성분
// 직선을 그리기 위한 기준점 역할을 함
x0 = a * rho;
y0 = b * rho;
// rho와 theta 값을 이용하여 직선의 시작점(p1)과 끝점(p2)을 계산함 (기울기 활용)
p1 = Point(cvRound(x0 + 1000 * (-b)), cvRound(y0 + 1000 * a));
p2 = Point(cvRound(x0 - 1000 * (-b)), cvRound(y0 - 1000 * a));
// 직선은 빨간색으로 표시되며, 선의 두께는 3, 선의 유형은 8-connected line -> result에 이미지를 차례로 표시함
line(result, p1, p2, Scalar(0, 0, 255), 3, 8);
}
imshow("Input image", image);
imshow("edge", edge);
imshow("Hough Transform", result);
waitKey(0);
}결과는 다음과 같다.


다음은 Houghlinesp(확률적 허프 변환)를 사용하여 직선을 검출하는 코드이다.
확률적 허프 변환은 더 빠르게 실행되며, 메모리 사용량도 줄이는 효과가 있다.
int main() {
Mat image, edge, result;
float rho, theta, a, b, x0, y0;
Point p1, p2;
vector<Vec4i> lines;
image = imread("chess_pattern.png"); // 이미지 로드함
result = image.clone(); // result 변수에 원본 이미지의 복사본을 생성함
cvtColor(image, image, CV_BGR2GRAY); // grayscale 이미지로 변환함
// grayscale 이미지에서 Edge를 검출함 (임계값 2개 -> 50, 200), 소벨 커널의 크기는 3
Canny(image, edge, 50, 200, 3);
//edge: input Mat, lines: output vector of lines
//1: (rho) distance resolution of the accumulator in pixels
//CV_PI/180: (theta) angle resolution of the accumulator in radians
//50: (threshold) accumulator threshold parameter
//10: (minLineLength) minimum line length.
//300: (maxLineGap) Maximum allowed gap between points on the
same line to link them
// 확률적 허프 변환을 사용하여 Edge 이미지에서 직선 segment를 검출함
// edge는 입력, lines는 검출된 직선 segment 저장 벡터, 1은 거리 해상도, CV_PI / 180은 각도 해상도
// 50은 직선 segment 임계값, 10은 최소 직선 길이, 300은 같은 직선으로 간주될 수 있는 최대 간격
HoughLinesP(edge, lines, 1, CV_PI / 180, 50, 10, 300);
for (int i = 0; i < lines.size(); i++) {
Vec4i l = lines[i];
// (l[0], l[1])은 선의 시작점 (시작점의 x, y 좌표), (l[2], l[3])은 선의 끝점 (끝점의 x, y 좌표)
line(result, Point(l[0], l[1]), Point(l[2], l[3]), Scalar(0, 0, 255), 3, 8);
}
imshow("Input image", image);
imshow("edge", edge);
imshow("Hough Transform", result);
waitKey(0);
}