⚛다익스트라 알고리즘이란?

음의 가중치가 없는 그래프의 한 정점(頂點, Vertex)에서 모든 정점까지의 최단거리를 각각 구하는 알고리즘(최단 경로 문제, Shortest Path Problem)이다.

• 처음 고안된 알고리즘은 O(v^2)의 시간 복잡도를 가졌다. 하지만 우선순위 큐를 이용한다면, O((V+E)logV)의 시간복잡도를 가지게된다.
• 그래프 방향의 유무는 상관 없으나, 간선들 중 단 하나라도 가중치가 음수이면 이 알고리즘은 사용할 수 없다.
• 음의 가중치를 가지는 간선이 있으며, 가중치가 음인 사이클이 존재하지 않는 경우 벨만 포드 알고리즘이 사용가능하다.

다익스트라 알고리즘 예

1. 1을 시작정점으로 잡고 1을 제외한 다른 모든 노드들과의 최소거리(최소 가중치)를 무한대로 설정한다.

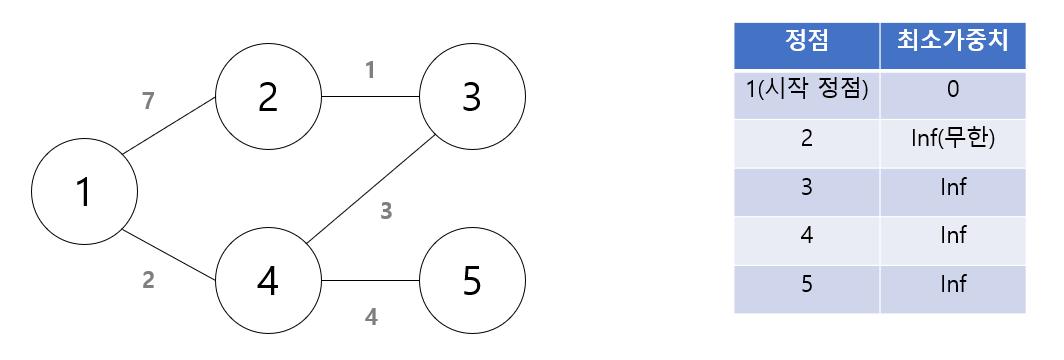
2. 가장 먼저 자기 자신을 방문한다. 방문한 노드와 연결된 노드들의 가중치를 조사하여, 연결된 노드의 최소 가중치를 갱신한다.
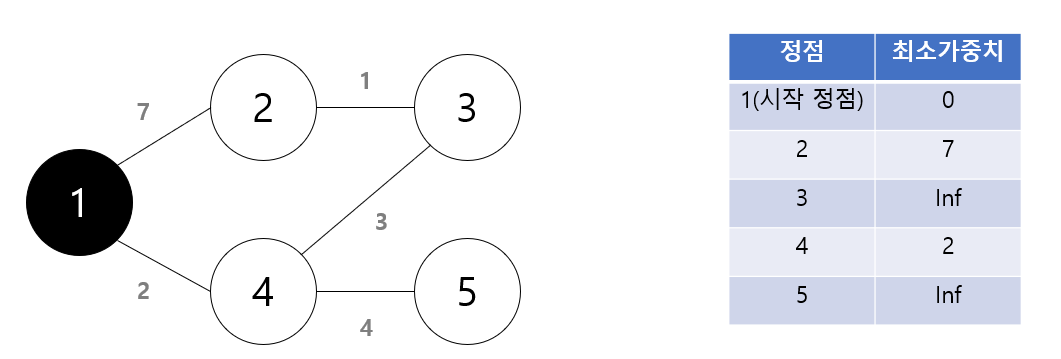
3. 연결된 노드들 중, 방문한 노드를 제외한, 모든 노드들 중 최소가중치가 가장 낮은 노드를 방문한다.
4. 방문 한 후, 자신 노드의 가중치 + 다음 노드의 가중치를 더한 값이 기존 최소 가중치보다 적을 경우, 갱신한다.

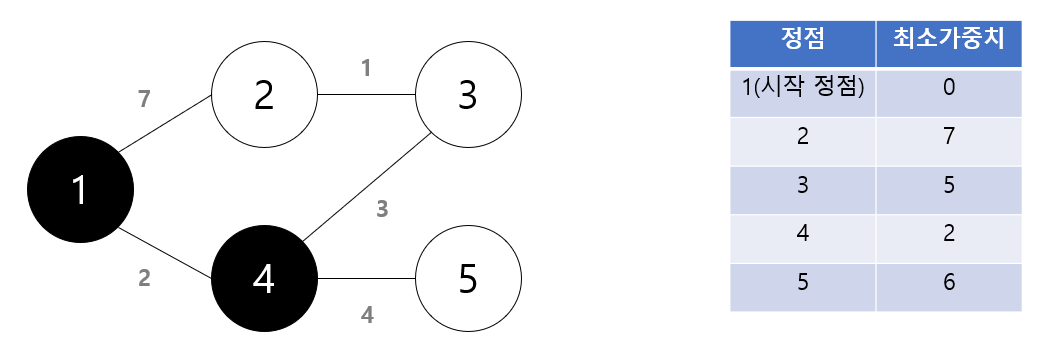
5. 위의 순서들을 모든 노드를 방문 할 때까지 계속해서 방문하고 최소 가중치를 갱신한다.

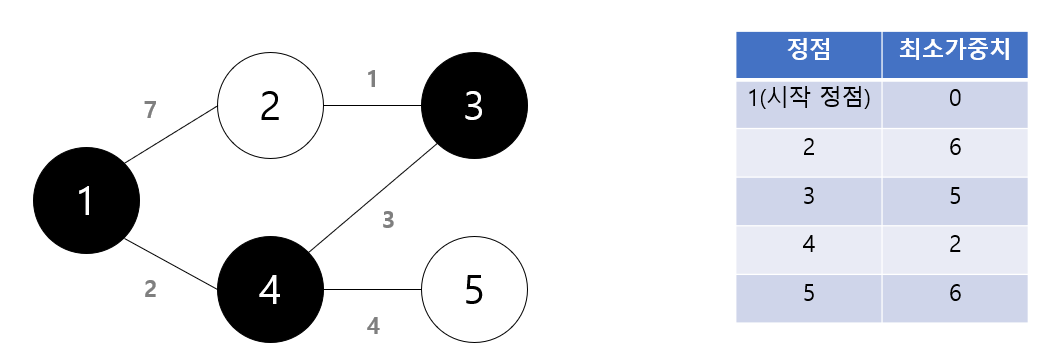
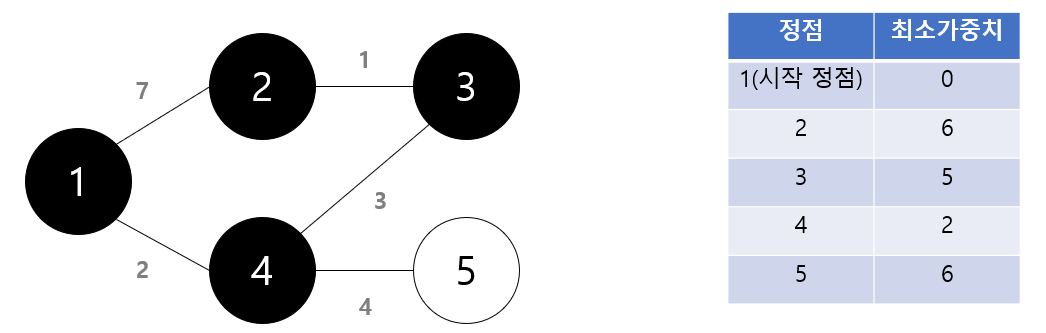
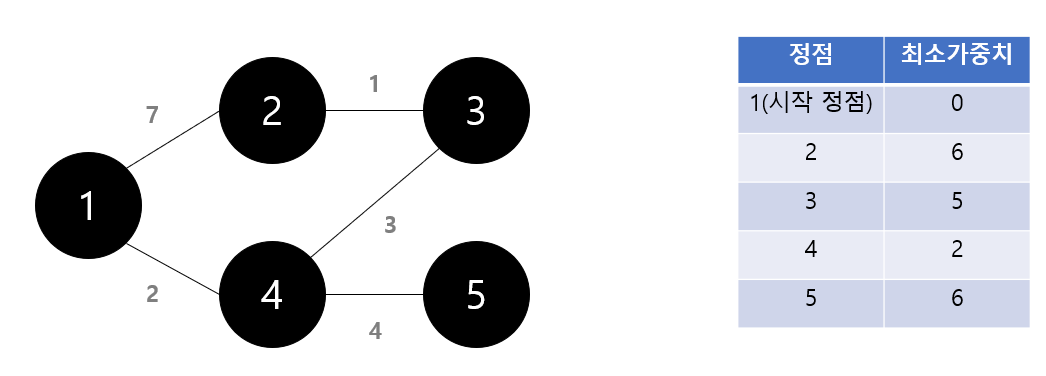
6. 마지막으로 모두 갱신된 최소 가중치로 시작 노드와 연결된 노드들의 최소 거리 값을 알 수 있다.

다익스트라 알고리즘 구현(힙사용, C++)

#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
#define INF 500000000 // 무한대

using namespace std;

int V, E, K;       //전체 정점의 개수, 간선의 개수, 시작점
int dist[20001];   // 최소가중치 테이블
vector<pair<int, int>> vertex[20001]; //그래프 전체 정보

void init();
void solve();
void dijkstra(int);

void init() {
	int u, v, w;

	cin >> V >> E >> K;

	for (int i = 0; i < E; i++) {
		cin >> u >> v >> w;
		
		vertex[u].push_back(make_pair(v,w)); // 그래프의 전체 정보를 벡터에 저장

	}
}
void solve() {
	fill_n(dist, V + 1, INF); // 최소 가중치 테이블 무한대로 초기화
	dijkstra(K); // 시작점이 K인 상태로 다익스트라 알고리즘 실행

	for (int i = 1; i <= V; i++) {
		if (dist[i] == INF) {
			cout << "INF\n";  // 정점이 무한대일 경우 INF 출력
		}
		else {
			cout << dist[i] << '\n'; //아니라면 해당 정점의 최소 가중치 값 출력 
		}
	}
}

void dijkstra(int start) {

	priority_queue<pair<int, int>> pq;  // 우선순위 큐 생성

	pq.push(make_pair(0,start));  // 시작점 정보를 힙에 push

	dist[start] = 0; // 시작점은 최소 가중치가 0으로 설정

	while (pq.empty() == 0) {
		
		int cur_w = -pq.top().first;  // 힙에 있는 값 중 가중치가 가장 작은 값을 꺼내와 정보를 저장
		int cur = pq.top().second; 

		pq.pop(); // 현재 정점에 대한 정보를 저장했으므로 빼준다.

		for (int i = 0; i < vertex[cur].size(); i++) {

			int next = vertex[cur][i].first; // 다음 정점에 대한 정보를 찾아 저장한다.
			int next_w = vertex[cur][i].second;

			if (dist[next] > cur_w + next_w) {
				
				dist[next] = cur_w + next_w;   //만약 현재 정점의 가중치와 다음 정점의 가중치를
																			 //더한 값이 기존 최소 가중치보다 작을 경우 갱신한다.
				pq.push(make_pair(-dist[next], next));  //최소 값으로 정렬해야하므로 음수를 붙여 힙에 넣는다.
			}
		}
	}
}

int main() {

	ios_base::sync_with_stdio(false);
	cin.tie(); cout.tie();

	init();
	solve();
}