에라토스테네스의 체
소수를 찾을 때 사용한다.
- 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
- 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
- 자기 자신을 제외한 2의 배수를 모두 지운다.
- 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
- 자기 자신을 제외한 3의 배수를 모두 지운다.
- 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
- 자기 자신을 제외한 5의 배수를 모두 지운다.
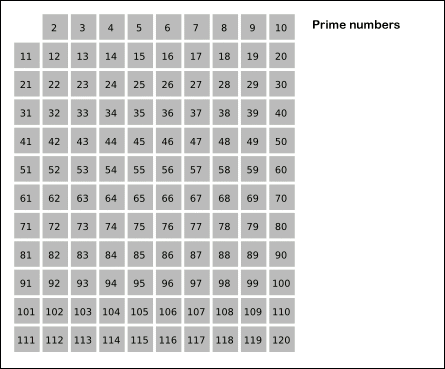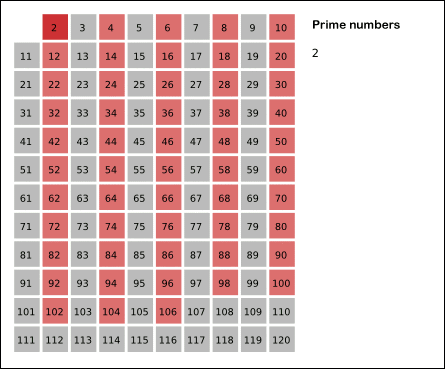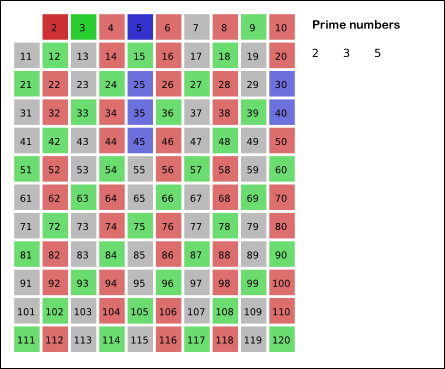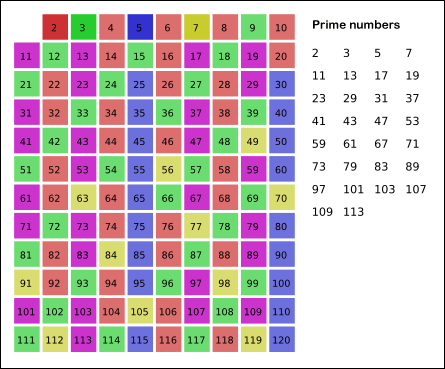
- 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
- 자기 자신을 제외한 7의 배수를 모두 지운다.
- 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
- 그림의 경우, 이므로 11보다 작은 수의 배수들만 지워도 충분하다. 즉, 120보다 작거나 같은 수 가운데 2, 3, 5, 7의 배수를 지우고 남는 수는 모두 소수이다.
- 위 설명처럼 에라토스테네스의 체를 구현하기 위해 숫자를 인덱스로 하는 배열을 생성한다. 배열이 가진 값은 해당 인덱스의 숫자가 소수인지를 나타낸다.
- 처음에는 모든 수를 소수라고 가정하여 초기화한다. 그리고 인덱스2(숫자2)부터 인덱스의 제곱수가 최대수보다 작을 때까지 해당 과정을 반복한다.
- 만약 인덱스의 숫자가 소수라고 여겨진다면 해당 소수를 배수로 하는 수를 모두 소수가 아니라고 표시해준다.
- 만약 인덱스의 숫자가 소수가 아니라면 그냥 넘어간다.
예제
소수 구하기
M이상 N이하의 소수를 모두 출력하는 프로그램을 작성하시오.- 에라토스테네스의 체의 기본개념을 물어보는 문제이다.
// isPrime은 모두 1로 초기화되어 있는 상태.
isPrime[1] = 0; // (1은 소수가 아니다)
for (int i = 2; i*i <= N; i++) {
if (isPrime[i]) {
for (int j = i*i; j <= N; j += i) { // 해당 수를 배수로 가지는 수를 모두 소수가 아니라고 표시한다.
isPrime[j] = 0;
}
}
}(응용) 제곱수로 나누어지지 않는 수 구하기
백준 1016 제곱 ㄴㄴ 수 - [풀이]
어떤 정수 X가 1보다 큰 제곱수로 나누어 떨어지지 않을 때, 그 수를 제곱ㄴㄴ수라고 한다.
제곱수는 정수의 제곱이다. min과 max가 주어지면, min보다 크거나 같고,
max보다 작거나 같은 제곱ㄴㄴ수가 몇 개 있는지 출력한다.- 에라토스테네스의 체에서 배수를 걸러내는 방법을 응용해서 문제를 풀 수 있다.
- 배열은 해당 숫자가 제곱수로 나누어지는지를 나타낸다.
- 인덱스2(숫자2)부터 인덱스의 제곱수가 최대수보다 작을 때까지 반복하는 것은 기본으로 똑같이 한다.
- 다만 해당 숫자가 소수인지 아닌지를 판별하지는 않는다.
- 여기서 최대가 될 수 있는 숫자가 으로 매우 크다. 따라서 min과 max의 범위값은 이므로 이를 이용해서, 해당 숫자의 배수를 범위 안에서만 세도록 한정시킨다.
- 배열을 탐색하며 제곱수로 나누어지지 않는 수(=1)를 확인한다.
for (long long i = 2; i*i <= maxx; i++) {
ii = i*i;
if (minn%ii == 0) mm = minn;
else mm = (minn/ii+1)*ii;
for (long long j = mm; j <= maxx; j += ii) {
isNini[j-minn] = 0;
}
}