Kunth, Morris, Prett 이름의 약자.

KMP

본문의 길이를 n이라 하고, 검색어의 길이를 m이라할 때, 문자열 검색을 빠르게 하기 위해 사용한다. 일반적인 검색 알고리즘에서는 비교 도중 다른 문자를 만났을 때, 시작점을 하나씩만 이동하여 진행한다.$O(nm)$ 하지만 KMP는 비교 도중 다른 문자를 만났을 때, 시작점을 특정 값만큼 이동하여 진행한다. 여기서 특정 값이란 현재 원문에서 비교중이었던 문자열의 크기에서, 그 문자열의 앞뒤로 겹치는 부분을 뺀 것이다. (비교중이었던 문자열의 앞부분과 뒷부분이 겹친다면 그 부분까지 점프해도 되기 때문이다.) $O(n+m)$

아래 사진은 원문 "안녕안녕하하안안녕하세요" 에서 "안녕하세요" 를 찾는 예시이다.

idx	1	2	3	4	5	6	7	8	9	10	11	12
	안	녕	안	녕	하	하	안	안	녕	하	세	요

1. 인덱스 1~2 까지 "안녕"이 찾는 문자열의 시작과 동일한 것을 확인하고, 인덱스 3을 확인한다.
   : 이때 인덱스3에는 "안"이 있고, 우리가 찾는 "하" 문자와 다른 것을 발견했다. 따라서 비교 시작점을 특정 값만큼 이동하여 진행한다.
   ⇒ 비교중이었던 문자열 크기(3. 안녕안) - 앞뒤로 겹치는 부분(1. 안-안) = 2.

2. 인덱스 1에서 +2한 인덱스3부터 다시 탐색한다. 인덱스 3~5 까지 "안녕하"가 찾는 문자열의 시작과 동일한 것을 확인하고, 인덱스 6을 확인한다.
   : 이때 인덱스6에는 "하"가 있고, 우리가 찾는 "세" 문자와 다른 것을 발견했다. 따라서 비교 시작점을 특정값만큼 이동하여 진행한다.
   ⇒ 비교중이었던 문자열 크기(4. 안녕하하) - 앞뒤로 겹치는 부분(0. $\emptyset$) = 4.

3. 인덱스 3에서 +4한 인덱스7부터 다시 탐색한다. 인덱스 7의 "안"이 우리가 찾는 문자열의 시작과 동일한 것을 확인하고, 인덱스 8을 확인한다.
   : 이때 인덱스8에는 "안"이 있고, 우리가 찾는 "녕" 문자와 다른 것을 발견했다. 따라서 비교 시작점을 특정값만큼 이동하여 진행한다.
   ⇒ 비교중이었던 문자열 크기(2. 안안) - 앞뒤로 겹치는 부분(1. 안-안) = 1.

4. 인덱스 7에서 +1한 인덱스8부터 다시 탐색한다.인덱스 8~13까지 "안녕하세요"는 우리가 찾는 문자열과 동일하다. 따라서 결과에 추가한다. (만약 이 뒤로 원문이 더 남아있다면, 비교 시작점을 동일한 방법으로 이동한다.)

겹치는 접두사, 접미사 (predecessor function, $\Pi$)

앞의 예시를 통해 시작점을 이동할 때 검색어의 앞뒤로 겹치는 부분의 문자 개수를 알아야 한다는 것을 생각할 수 있다.
그럼 문자열의 앞의 부분을 접두사(prefix), 뒤의 부분을 접미사(suffix) 라 하고, 문자열에서 일치하는 접두사와 접미사의 길이를 먼저 구해보자.

"안녕안녕안녕하" 라는 검색어의 접두사와 접미사의 길이를 구한 것은 다음과 같다. 문자열의 시작부부은 인덱스 0이며, Pi[i]는 0부터 i까지의 접두사와 접미사의 길이를 구하여 넣은 것이다.

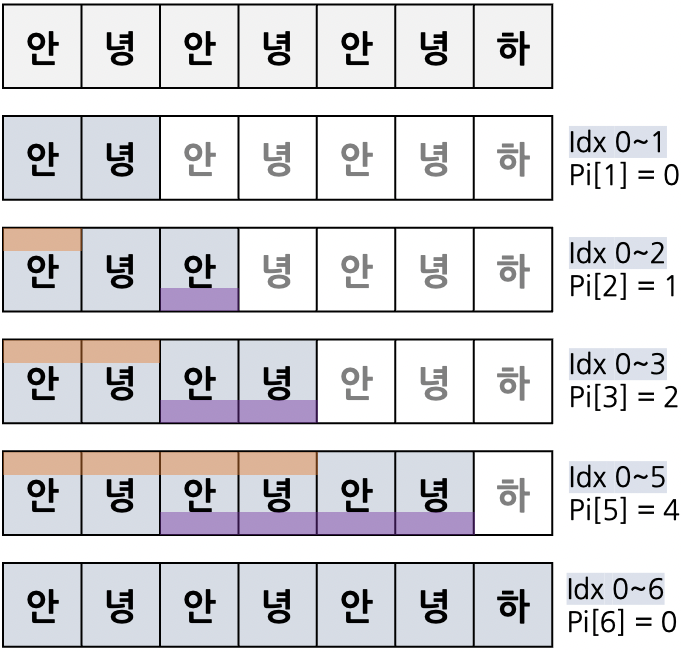
놀랍게도 이 또한 kmp 알고리즘으로 구할 수 있다. 접두사와 접미사의 동일한 부분을 구하는 것은, kmp의 원문을 "안녕안녕안녕하"라고 생각하고, 검색어를 "안녕안녕안녕하"라고 둔것과 동일하다.
코드로 나타내면 다음과 같다. $O(m)$

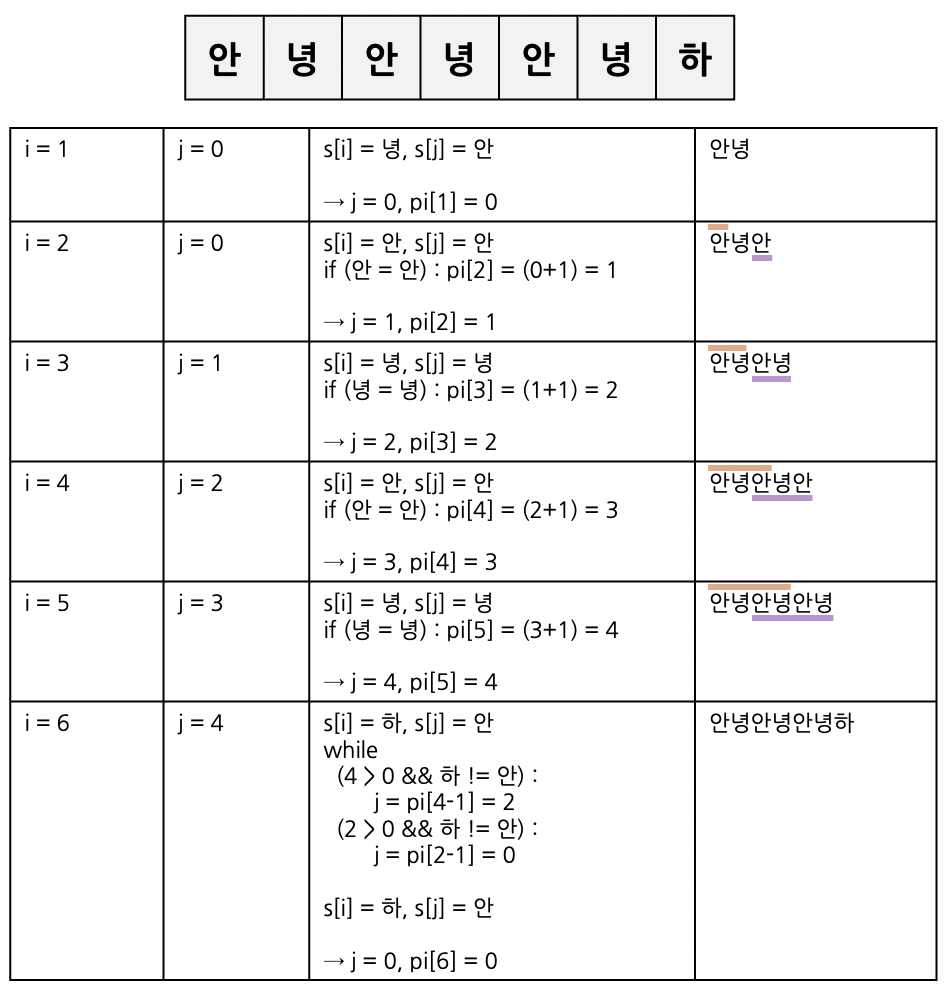
int j = 0;
for (int i = 1; i < s.length(); i++) {
	while (j > 0 && s[i] != s[j]) {
    	j = pi[j-1];
    }
    if (s[i] == s[j]) {
    	pi[i] = ++j;
    }
}  

1. 처음에 j를 0으로 두고, i를 1부터 시작하여 모든 문자열을 탐색할 때까지 다음을 반복한다.
2. 만약, s[i]와 s[j]가 같지 않고 j 또한 1 이상의 수를 가질 때, 이를 만족하지 않을 때까지 다음을 반복한다.
   • j = pi[j-1]
3. 만약, s[i]와 s[j]가 같을 때, j를 1 증가시키고, pi[i] 에 해당값을 넣는다.

얼핏 단순한 식이지만 동시에 이해하기 어렵다. 다음 예시가 동작하는 과정은 다음과 같다.

검색

int j = 0;
int n = original_string.length();
int m = search_string.length();
vector<int> pi = getPi(); // 위의 전처리

for (int i = 0; i < n; i++) {
	while (j > 0 && original_string[i] != search_string[j]) {
    	j = pi[j-1];
	}
    if (original_string[i] == search_string[j]) {
    	if (j == m-1) {
        	ans.push_back(i-m+1);
            j = pi[j];
		}
		else {
    		++j;
        }
	}
}

1. 처음에 j를 0으로 두고, i를 0부터 시작하여 모든 원문의 문자열을 탐색할 때까지 다음을 반복한다.
2. 만약, original_string[i]와 search_string[j]가 같지 않고 j 또한 1 이상의 수를 가질 때, 이를 만족하지 않을 때까지 다음을 반복한다. (점프하는 단계)
   • j = pi[j-1]
3. 만약, original_string[i]와 search_string[j]가 같을 때,
   3-1. 현재 j가 m-1과 같다면 (즉, 검색어의 마지막까지 동일하다면) 정답에 해당 시작 인덱스를 추가하고, j에 pi[j] 값을 넣는다.
   3-2. 현재 j가 m-1과 같지않다면 (즉, 검색어의 마지막까지 확인하지 못 했다면) j를 1 증가시킨다.

예제

백준 1786 찾기 - [풀이]

워드프로세서 등을 사용하는 도중에 찾기 기능을 이용해 본 일이 있을 것이다. 이 기능을 여러분이 실제로 구현해 보도록 하자.

두 개의 문자열 P와 T에 대해, 문자열 P가 문자열 T 중간에 몇 번, 어느 위치에서 나타나는지 알아내는 문제를 '문자열 매칭'이라고 한다. 
워드프로세서의 찾기 기능은 이 문자열 매칭 문제를 풀어주는 기능이라고 할 수 있다. 이때의 P는 패턴이라고 부르고 T는 텍스트라고 부른다.
....
T와 P가 주어졌을 때, 문자열 매칭 문제를 해결하는 프로그램을 작성하시오.

• KMP 기본개념적 문제