최소 스패닝 트리

• 스패닝 트리 (Spanning Tree)
  : 모든 꼭짓점을 포함하는 부분 그래프 = 즉, 모든 노드가 간선으로 서로 연결되어 있다. 하지만 사이클을 이루어서는 안 되며, 따라서 간선의 개수(n-1)는 노드의 개수(n)보다 하나 적어야 한다. (cf. 단방향 간선들이 사이클을 이루는지 확인하는 방법 - [위상정렬])
• 최소 스패닝 트리 (Minimum Spanning Tree)
  : 간선의 가중치 합이 최소인 스패닝 트리. 마찬가지로 사이클을 이루어서는 안 되며, 간선의 개수는 노드의 개수보다 하나 적어야 한다.
  

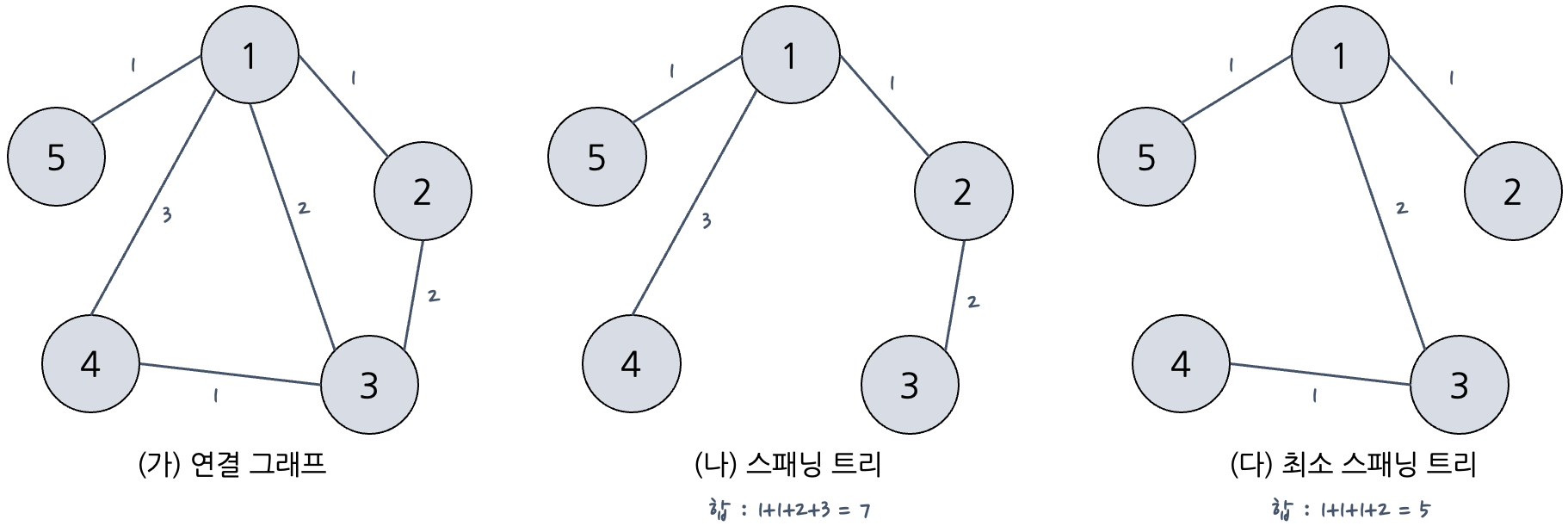
최소 스패닝 트리의 특징을 통해 노드들을 최소 비용으로 모두 연결할 수 있는 간선을 선택할 수 있다.

아래는 최소 스패닝 트리 MST를 구현하는 방법이다.

크루스칼 Kruskal

1. 간선들을 비용순으로 오름차순 정렬한다. $O(E\log{E})$
2. 사이클을 이루지 않도록 간선들을 차례대로 선택한다. 만약 n-1개의 간선들이 모두 뽑혔으면 최소 스패닝 트리가 만들어진 것이므로 종료한다.

• 정렬한 간선들을 차례대로 뽑으면 자연스럽게 최소합이 완성된다. 하지만 뽑은 간선들이 사이클을 이루는지는 어떻게 확인할까? 만약 a, b 노드를 잇는 간선 하나를 뽑아 둘을 이으려고 할 때, a, b 가 이미 다른 간선을 통해 이어져 있다면 사이클이 발생하게 된다. 따라서 a, b 노드가 같은 집합에 있다면 해당 간선을 선택하지 않아야 한다. 이를 위해 양방향 간선들로 이루어진 그래프가 사이클을 이루는지 확인하는 union-find 방법이 있다.

union-find 알고리즘

• union : 합집합, 즉 합집합 찾기
• 본인이 어느 부모의 자식인지를 나타낼 수 있도록 한다. 만약 두 노드가 같은 노드를 지녔다면, 두 노드는 같은 집합에 존재한다는 뜻이다.
  - 이때 조상 노드가 동일할 수도 있기 때문에 부모 노드의 부모 노드까지 탐색해야 한다.
• 같은 집합이 아닌 두 노드를 합칠 때, 더 작은 값을 가진 노드a를 노드b의 부모로 정한다. $parent[b] = a \,(a<b)$ (union)

크루스칼 + union-find 과정

위 과정을 정리하면 다음과 같다.

1. 간선들을 비용순으로 오름차순 정렬한다.
2. 사이클을 이루지 않도록 간선들을 차례대로 선택한다.
   2-1. 사이클을 판별하는 방법으로 union-find를 사용한다. 만약 부모가 같다면 해당 간선을 잇지 않는다.
   2-2. 부모가 다르다면 간선을 잇고, 한 쪽 노드의 부모 노드를 재정의한다.
3. 만약 n-1개의 간선들이 모두 뽑혔으면 최소 스패닝 트리가 만들어진 것이므로 종료한다.

1. 간선들을 비용이 작은 순으로 오름차순 정렬한다. (위 그림과 달리 2-5를 잇는 간선을 하나 더 추가했다.)
   parent[i] 는 i의 부모 노드를 뜻한다. 처음에는 자기 자신을 가리키도록 한다.
   

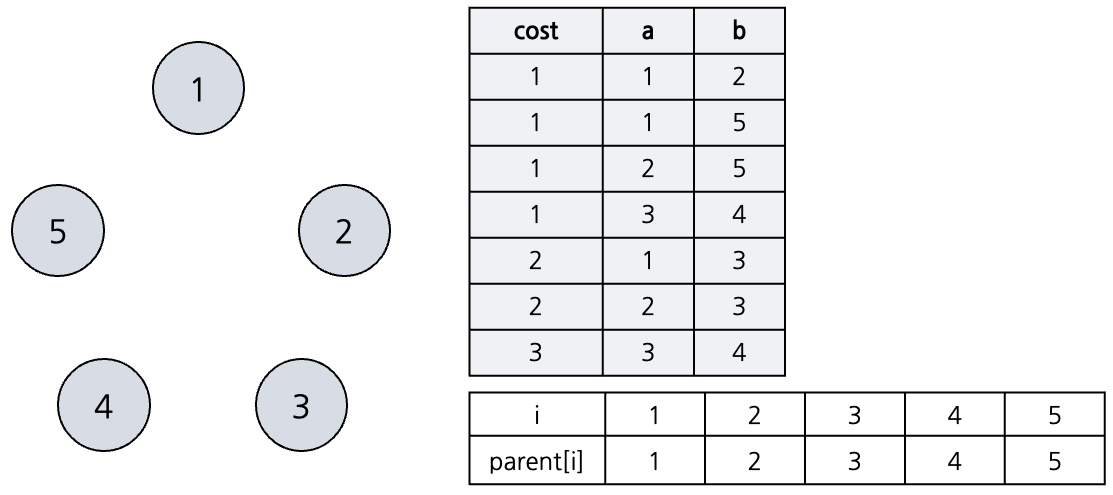
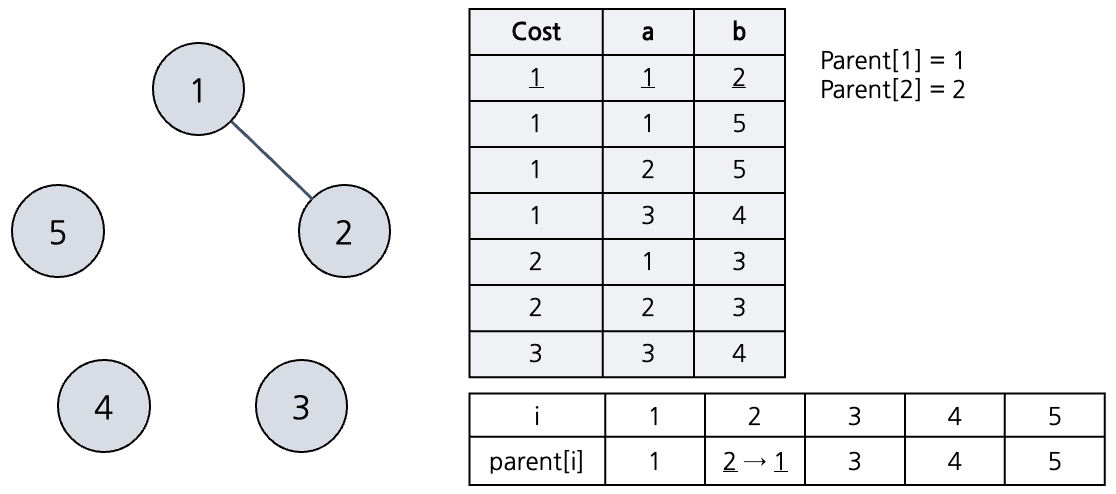
2. 첫번째 간선을 택한다. 노드 1, 2를 잇는 간선이므로 노드 1, 2의 부모를 조사해보자. 둘의 부모 노드는 1, 2로 다른 것을 알 수 있다. 따라서 두 노드를 해당 간선으로 이어도 사이클이 발생하지 않는다. 간선을 연결해주고 union-find 를 위해 노드2의 부모 노드를 1 로 바꾸어준다.
   

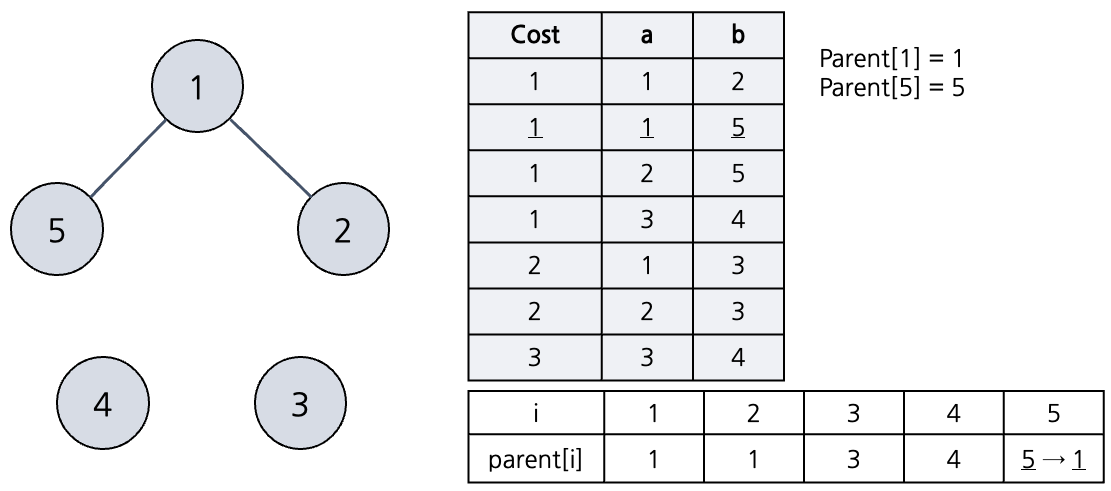
3. 다음 두번째 간선을 택한다. 노드 1, 5를 잇는 간선이므로 노드 1, 5의 부모를 조사해보자. 둘의 부모 노드는 1, 5로 다른 것을 알 수 있다. 따라서 두 노드를 해당 간선으로 이어도 사이클이 발생하지 않는다. 간선을 연결해주고 union-find 를 위해 노드5의 부모 노드를 1 로 바꾸어준다.
   

4. 다음 세번째 간선을 택한다. 노드 2, 5를 잇는 간선이므로 노드 2, 5의 부모를 조사해보자. 둘의 부모 노드는 1, 1로 서로 같다. 따라서 두 노드를 해당 간선으로 이으면 사이클이 발생한다. 그러므로 간선을 연결하지 않고 다음 간선으로 넘어간다.
   

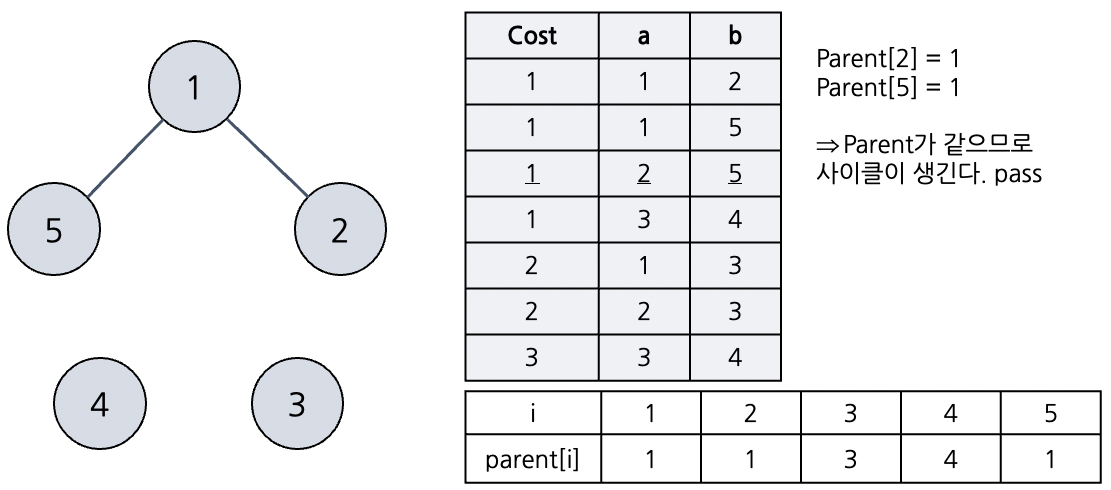
5. 다음 네번째 간선을 택한다. 노드 3, 4를 잇는 간선이므로 노드 3, 4의 부모를 조사해보자. 둘의 부모 노드는 3, 4로 다른 것을 알 수 있다. 따라서 두 노드를 해당 간선으로 이어도 사이클이 발생하지 않는다. 간선을 연결해주고 union-find 를 위해 노드4의 부모 노드를 3 로 바꾸어준다.
   

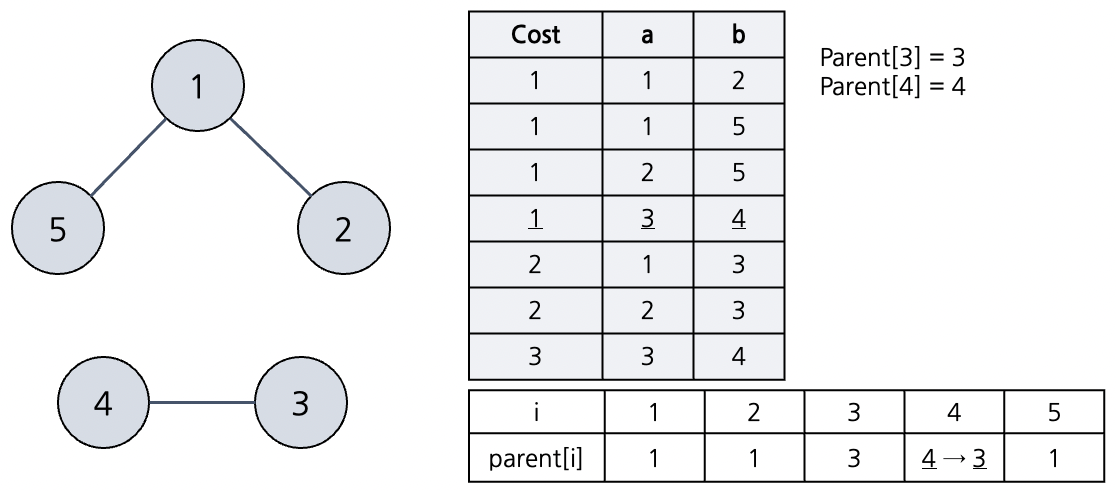
6. 다음 다섯번째 간선을 택한다. 노드 1, 3을 잇는 간선이므로 노드 1, 3의 부모를 조사해보자. 둘의 부모 노드는 1, 3로 다른 것을 알 수 있다. 따라서 두 노드를 해당 간선으로 이어도 사이클이 발생하지 않는다. 간선을 연결해주고 union-find 를 위해 노드3의 부모 노드를 1 로 바꾸어준다.
   간선 4개를 다 선택했으므로 중단한다.
   

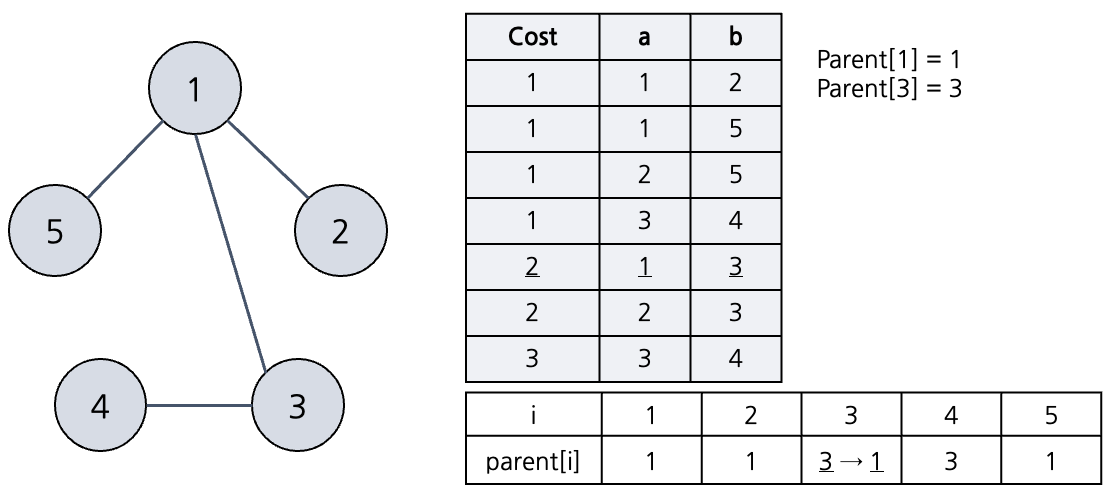
int find_parent(int node) {
    if (parent[node] != node) return find_parent(parent[node]);
    return node;
}

int kruskal() {
    sort(edge.begin(), edge.end()); // 1. 오름차순 정렬
    
    for (int i = 1; i <= N; i++) {
        parent[i] = i;
    }

    int node1, node2, cost, n1_parent, n2_parent, ans = 0;
    for (int i = 0; i < edge.size(); i++) {
        node1 = edge[i].second.first;
        node2 = edge[i].second.second;
        cost = edge[i].first;
        n1_parent = find_parent(node1); // 2.
        n2_parent = find_parent(node2);
        if (n1_parent != n2_parent) {	// union-find
            ans += cost;
            parent[n2_parent] = n1_parent;
        }
    }
}

프림 Prim

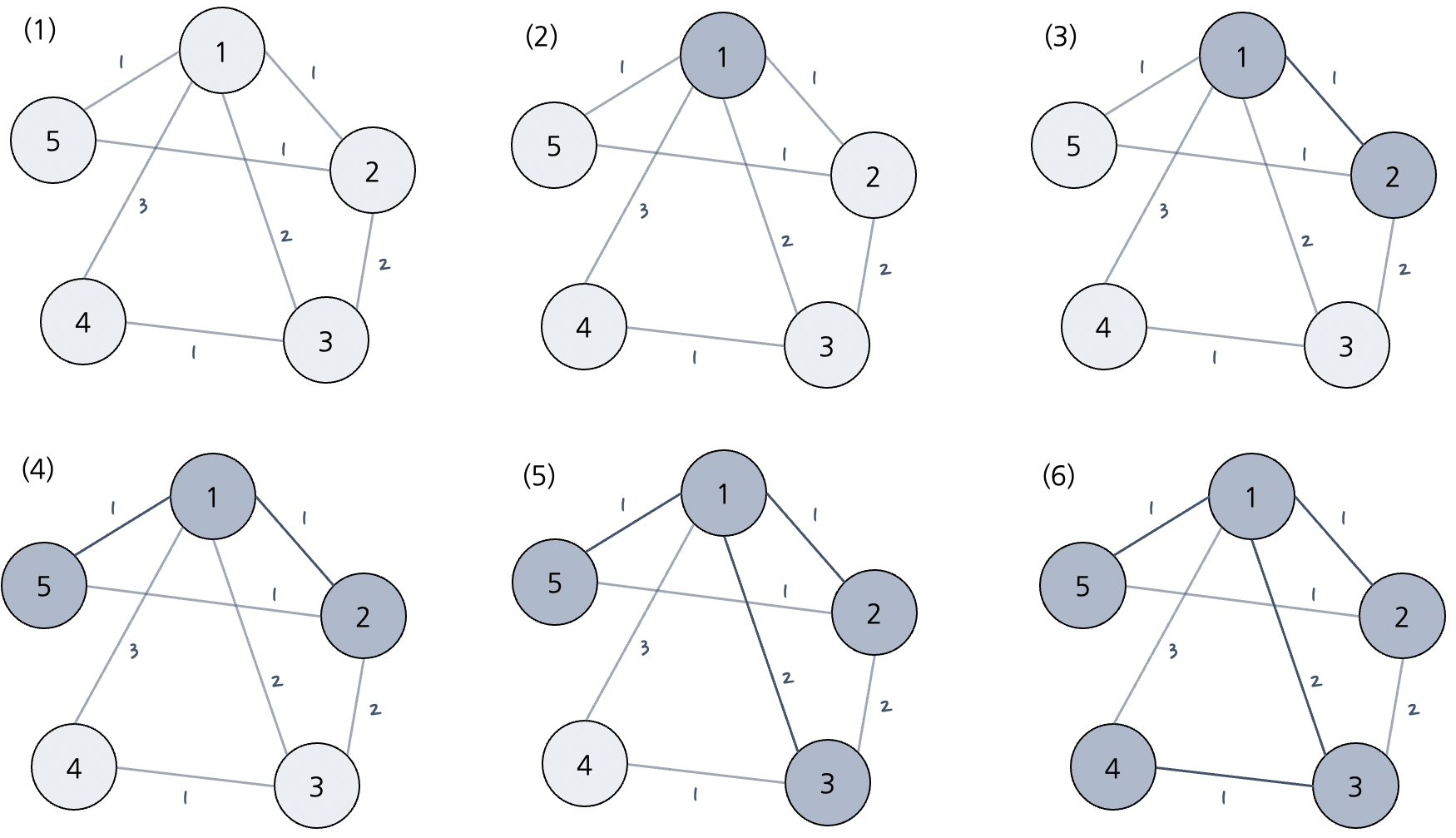
1. 임의의 노드를 하나 선택한다. 해당 노드는 이제 <연결된 노드 집합>에 포함된다.
2. <연결되지 않은 노드 집합>의 노드와 <연결된 노드 집합>의 노드를 잇는 간선 중 가장 짧은 간선을 선택한다.
3. 이렇게 새로 연결된 노드를 추가한 <연결된 노드 집합>의 노드와 <연결되지 않는 노드 집합>의 노드를 잇는 간선 중 가장 짧은 간선을 다시 선택한다.
   • <연결되지 않은 노드 집합>-<연결된 노드 집합>의 간선을 택하는 행위이므로 사이클이 발생하지 않는다.

like 다익스트라
1. (cost, node) 를 담는 우선순위 큐를 만든다. 그리고 시작점 1을 비용 0으로 집어넣는다.
2. 노드의 수만큼 다음을 반복한다. {
3. 큐가 빌때까지 다음을 반복한다. [
4. 큐에서 꺼낸 top의 노드가 연결되어 있지 않은 노드라면 min_dist를 갱신하고 반복을 빠져나온다.
5. 만약 연결된 노드라면 필요없으므로 pop하고 다음 top을 꺼낸다. ]
6. 갱신된 min_dist를 정답에 더하고, 새로운 노드가 연결되면서 추가로 선택할 수 있게된 간선들(새 노드를 출발점으로 한)을 큐에 집어넣는다. }

int prim() {
    priority_queue<pair<int, int> > que;
    que.push(make_pair(0, 1)); // cost 0, 출발 노드가 1

	for (int i = 1; i <= N; i++) {
    	int top_node = -1, min_dist = INF;
        
	    while (!que.empty()) {
    	    top_node = que.top().second; int top_cost = que.top().first;
			if (!connected[top_node]) {
            	min_dist = top_cost;
                break;
			}
            
        	que.pop();
		}
        ans += min_dist;
        connected[top_node] = true;
        for (int i = 0; i < edge[top_node].size(); i++) {
        	que.push(i);
		}
    }
}

(크루스칼 vs 프림)

• 크루스칼 $O(E\log{E})$ - 간선(E)이 적은 경우 프림보다 좋다.
• 프림 $O(E\log{V})$ - 간선(E)이 많은 경우 크루스칼보다 좋다.