분리집합이란
분리 집합(Disjoint Set, Union-Find)은 코테에서 중요한 자료구조로 나타남
Disjoint Set(분리 집합, 서로소 집합)이란 서로 공통된 원소를 가지고 있지 않은 2개 이상의 집합을 말함
분리집합은 여러 노드가 서로 중복되지 않는 집합으로 나누어져 있을 때, 각 집합을 대표하는 노드 하나를 선택해 그 집합을 대표하도록 구성함
분리 집합의 활용 유형
💡- 사이클 판별
- 그래프에서 사이클이 있는 지 확인할 때 사용함
- 간선을 하나씩 추가하면서 두 노드의 루트 노드가 같다면 사이클이 생성된 것
- Kruskal 알고리즘에서 MST를 구할 때 사이클 확인 용도로 사용됨
- 집합의 병합 및 찾기 연산
- 두 집합을 하나로 합치거나, 어떤 원소가 어떤 집합에 속하는 지 찾을 때 사용됨
- 네트워크 연결
- 여러 네트워크가 연결되어 있을 때, 두 네트워크가 연결되어 있는지 확인하거나 연결할 때 사용
- 모양 인식
- 이미지나 그래프에서 같은 모양의 그룹을 판별하는 문제에서 사용될 수 있음
- 동등 관계 문제
- 두 원소가 같은 집합에 속해 있는 지 확인하는 문제에서 사용됨
분리 집합의 3가지 연산
- Make set : 분리 집합을 초기화하는 연산
- Find : 원소가 속한 집합의 대표 원소(루트 노드)를 찾음
- Union : 원소가 속한 집합의 대표 원소를 찾음
Make-Set
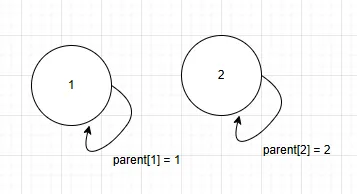
- i번째 노드의 루드 노드를 i번째 노드로 설정하는 것 → 자기 자신이 루트 노드가 되는 것임
- 보통 parent라는 배열을 선언해서 초기화함
코드
const int SIZE = 100001;
int parent[SIZE];
// 1번부터 SIZE - 1번의 노드를 초기화함
void init() {
for (int i = 0; i < SIZE; i++) {
parent[i] = i;
}
}
Find
Find 연산은 어떤 원소가 주어졌을 때 이 원소가 속한 집합의 대표 원소(루트 노드)를 반환하는 연산임
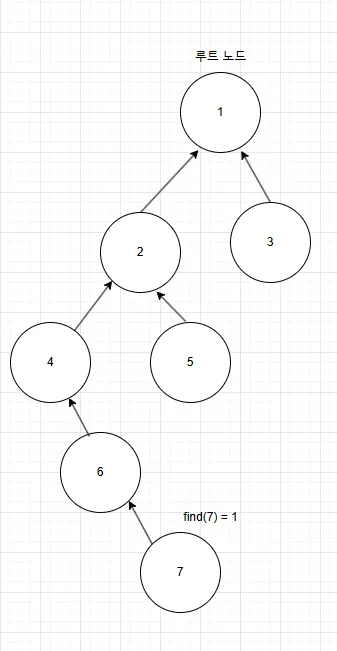
위 사진처럼 7이라는 노드에 find 연산을 하면 1이라는 값을 반환해야됨
이걸 단순하게 구현하려면 이렇게 구현하면 됨
일반적인 Find 연산
int find(int x) {
if (x == parent[x])
return x;
return find(parent[x]);
}하지만 위 사진을 예시로 들어서 find(7)이라는 연산을 실행했을 때는 다음과 같음
재귀 과정
find(7)→7의 부모6,find(6)호출find(6)→6의 부모4,find(4)호출find(4)→4의 부모2,find(2)호출find(2)→2의 부모1,find(1)호출find(1)→1 == parent[1], 루트 노드이므로1반환
총 5번의 함수 호출
만약, n번째 노드가 n level이라면 O(n)의 시간복잡도를 가지게 됨
find연산을 n번 호출하면 O()이라는 시간복잡도를 갖게 됨 이는 매우 비효율적임
이런 문제를 해결하기 위해 경로 단축을 활용함
경로 단축을 사용한 find연산 코드
int find(int x) {
if (x == parent[x])
return x;
return parent[x] = find(parent[x]);
}위 코드와 차이점은 return parent[x]를 할 때 find(parent[x])의 반환값으로 초기화한 뒤 반환한다는 점이다.
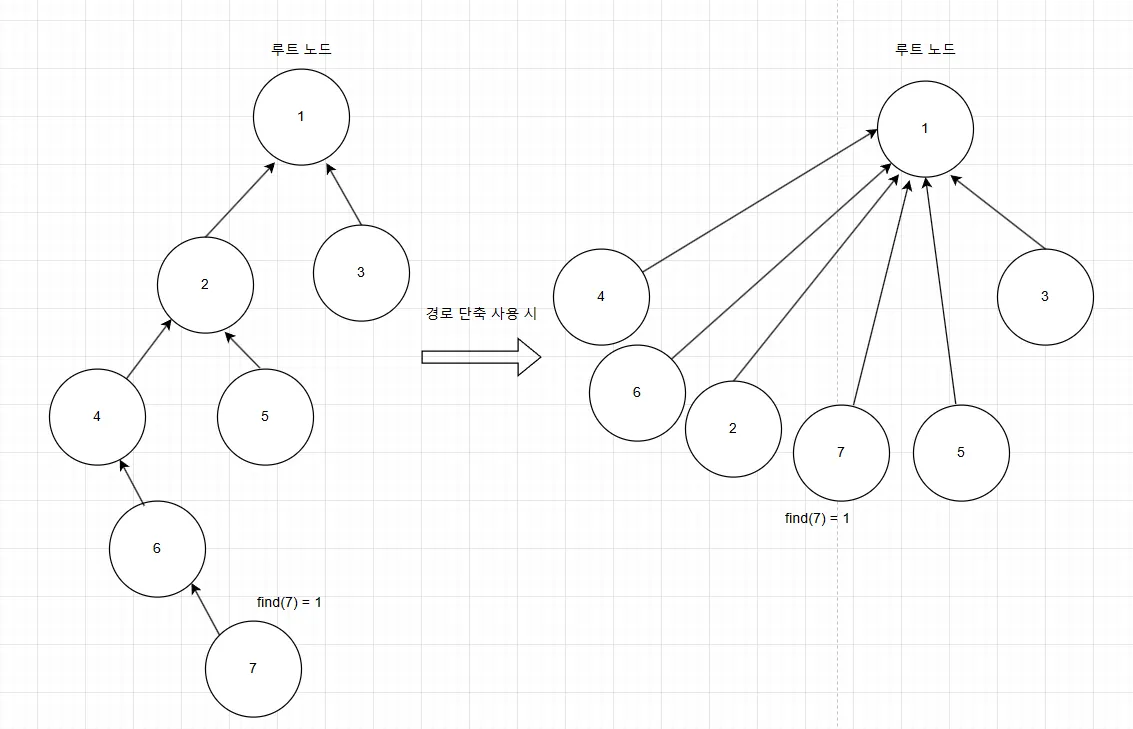
개선된 find 연산을 통해 위와 동일한 find(7)을 실행해보자
동작 과정
find(7)→return parent[7] = find(parent[7])⇒find(6)호출, 이때parent[7]은find(6)의 반환값으로 초기화됨- find(6) →
return parent[6] = find(parent[6])⇒find(4)호출, 이때parent[6]은find(4)의 반환값으로 초기화됨 - find(4) →
return parent[4] = find(parent[4])⇒find(2)호출, 이때parent[4]은find(2)의 반환값으로 초기화됨 - find(2) →
return parent[2] = find(parent[2])⇒find(1)호출, 이때parent[2]은find(1)의 반환값으로 초기화됨 - find(1) → parent[1] == 1 ⇒ return 1
결과 ⇒ parent[7], parent[6], parent[4], parent[2]의 값이 모두 1로 초기화됨
이는 추후에 7의 직계 조상 (부모, 부모의 부모, …) 노드들에 find 연산을 했을 때 O(1)의 시간 복잡도를 갖게 해준다.
Union
두 개의 집합을 하나의 집합으로 합치는 연산이다.
즉, 한 트리의 루트를 다른 트리의 루트에 연결하여 두 트리를 하나로 결합한다.
Union 과정은 다음과 같다.
- find 연선을 통해 두 요소의 루트 노드를 찾는다.
- 찾은 두 루트 노드를 비교한다.
- 같으면, union 연산을 중단한다.
- 다르면, 두 루트 노드 중 하나를 다른 트리의 루트 노드 아래에 배치하여 두 트리를 합친다.
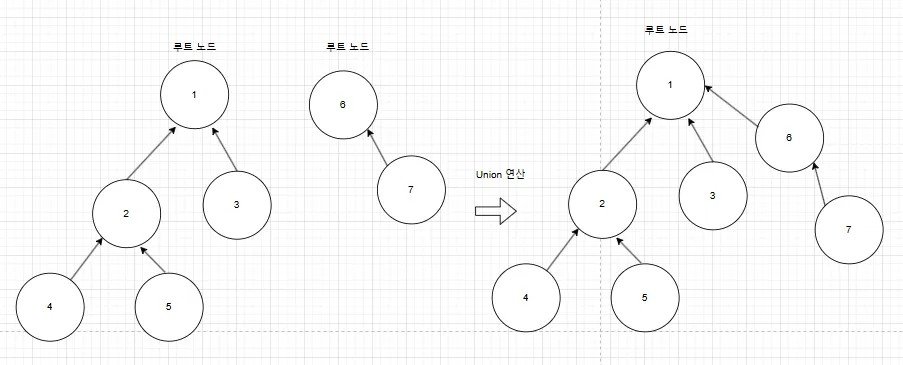
union 연산을 하면 그림과 같이 되는 것이다.
일반 union 연산 코드
// x, y 두 요소의 루트 노드를 찾은 뒤, y의 루트 노드를 x의 루트 노드 아래로 연결시킨다.
void merge(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX == rootY) {
return;
}
parent[rootY] = rootX;
}하지만 이 방식의 최악의 경우 다음과 같은 선형 트리가 생길 수 있음
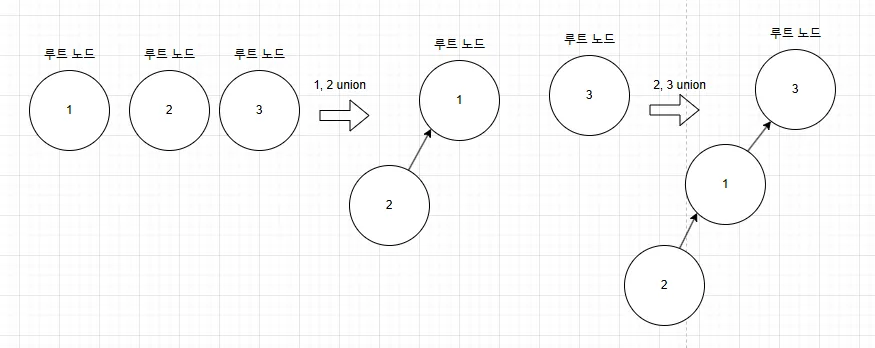
이런 경우, find 연산이 O(n)이라는 시간복잡도를 갖게 됨
개선된 union 연산 코드
두 트리를 합칠 때 트리의 높이(깊이, rank)를 기준으로 더 작은 트리를 더 큰 트리 아래에 연결한다.
직관적인 이유
높이가 더 낮은 트리를 더 큰 트리 아래에 연결하면, 합쳐진 트리의 최대 높이는 증가하지 않거나 1만큼만 증가함
이를 통해 균형을 유지하면서 트리의 깊이가 비정상적으로 커지는 것을 방지할 수 있음
이를 Union by Rank 기법이라고 한다.
증명
- 기본 가정
- 처음 각 원소가 자기 자신을 부모로 가지므로 모든 집합의 트리의 높이는 0
- Rank는 트리의 높이를 의미함
- Rank 증가 조건
- 두 트리를 합칠 때 Rank가 같은 경우에만 높이 (Rank)가 증가함
- 두 트리의 높이가 모두 h라면, 두 트리를 합친 결과의 높이는 h+1이 됨
- Rank의 최대값
- Rank가 증가하는 횟수는 제한적임
- 노드가 합쳐질 때마다 한 쪽 트리의 Rank는 그대로 유지되고, 다른 쪽 트리의 Rank가 증가함
- n개의 노드가 있을 때, 트리의 Rank는 최대 log N을 넘지 않음
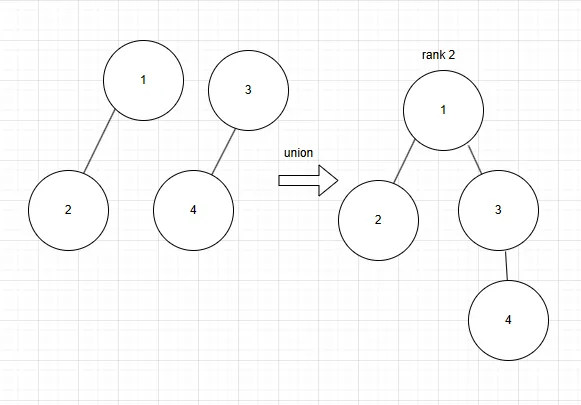

- 사진처럼 트리의 높이가 1 증가할 때마다 합쳐지는 두 트리는 서로 다른 집합이고, 이러한 과정이 반복될 때마다 트리에 속한 노드의 수가 두 배씩 증가하기 때문에 Rank가 증가하는 횟수는 제한적임
- 귀납적 증명
-
Base case
1개의 노드만 있을 때 트리의 높이 h = 0
-
Hypothesis
Union by Rank를 사용해서 두 트리를 합친 트리의 노드 수가 k개 일 때, 트리의 높이는 를 넘지 않는다고 가정
-
귀납
두 개의 높이가 이하인 트리를 합치면
- Rank가 증가하는 경우는 두 트리의 높이가 같을 때만 발생함
- 이때, 합쳐진 트리의 높이는 가 됨
- 이 경우 트리의 노드 수는 가 됨
이때, 트리의 최대 높이는 를 넘지 않음
따라서 Union by Rank를 사용해서 두 트리를 합친 트리의 노드 수가 N개일 때 트리의 높이는 최대 이 됨
-
개선 코드
int parent[SIZE];
int ranking[SIZE];
void init() {
for (int i = 0; i < SIZE; i++) {
parent[i] = i;
ranking[i] =0;
}
}
//find는 동일
void merge(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX == rootY) {
return;
}
if (ranking[rootX] > ranking[rootY]) {
parent[rootY] = rootX;
}
else if(ranking[rootX] < ranking[rootY]) {
parent[rootX] = rootY;
}
else {
ranking[rootX]++;
parent[rootY] = rootX;
}
}union-find 시간복잡도
최적화를 하지 않은 union-find의 시간복잡도는 O(N) 이다. (N은 노드의 수)
경로 압축과 union by rank를 적용한 union-find의 시간복잡되는 O(α(N))이다.
O(α(N))는 아커만 역함수로 매우 느리게 증가하는 함수로 N이 이어도 아커만 역함수는 4 이하이다.
따라서, 실제 문제에서는 O(1)과 같다.
번외
Weighted Union-Find
부모와의 관계를 나타내는 가중치를 저장하며, 상대적 관계나 거리, 값을 유지하는 데 사용할 수 있다.
💡사용예시
- 상대적 거리 계산
- 좌표계 문제
- 누적 비용 계산 등
예시 코드
const int SIZE = 100001;
int parent[SIZE];
int weight[SIZE];
void init() {
for (int i = 0; i < SIZE; i++) {
parent[i] = i;
weight[i] = 0;
}
}
int find(int x) {
if (x != parent[x]) {
int root = find(parent[x]); // 루트 노드 찾기
weight[x] += weight[parent[x]]; // 가중치 누적
parent[x] = root; // 경로 압축
}
return parent[x];
}
void merge(int x, int y, int w) {
int rootX = find(x);
int rootY = find(y);
if (x == y) {
return;
}
parent[rootY] = rootX;
weight[rootY] = weight[x] - weight[y] + w;
// weight[x] : 노드x와 루트 노드와의 상대적 가중치
// weight[y] : 노드y와 루트 노드와의 상대적 가중치
// w : 노드x와 노드y 사이의 직접적인 가중치
// weight[x] - weight[y] : 노드x와 루트 노드와의 상대적 가중치
// 이를 통해 x와 y 간의 기존 상대적 가중치 관계를 유지함
// + w : x와 y 사이에 새로운 가중치 w를 추가함
// 결과 weight[rootY]는 rootY가 rootX 아래로 병합될 때, rootY와 rootX 간의 가중치
// 차이를 정확히 반영함
}
weight[rootY] = weight[x] - weight[y] + w의 관한 GPT의 부가 설명
예시
- 노드 1 → 노드 2: 가중치 4
- 노드 2 → 노드 3: 가중치 3
이때, unionWeighted(1, 2, 4)와 unionWeighted(2, 3, 3)를 호출한다고 가정합니다.
과정
unionWeighted(1, 2, 4)실행 시:weight[root2] = weight[1] - weight[2] + 4- 초기 가중치가 0이므로:weight[2]=0−0+4=4 weight[2]=0−0+4=4
unionWeighted(2, 3, 3)실행 시:weight[root3] = weight[2] - weight[3] + 3- 현재
weight[2] = 4이므로:weight[3]=4−0+3=7 weight[3]=4−0+3=7
결과
- 노드 1 → 노드 2의 가중치: 4
- 노드 2 → 노드 3의 가중치: 3
- 노드 1 → 노드 3의 상대적 가중치: 4+3=7 4+3=7
정리
수식 weight[rootY] = weight[x] - weight[y] + w;는:
- 노드
x와 노드y가 속한 집합을 병합할 때, - 기존의 상대적 가중치와 새로운 가중치
w를 조정하여 - 가중치 관계를 유지하면서 두 집합을 하나로 합치는 역할을 합니다.
이 수식을 통해 가중치 기반의 Union-Find에서 각 노드 간의 상대적인 관계나 거리 값을 정확하게 관리할 수 있습니다. 🚀
