1 정의 - 스파셜 도메인 처리, 강도 변환
2 기본 강도 변환 함수 - 음수, 로그, 제곱, 조각
3 확률 변수&PDF
4 히스토그램 균등화
5 히스토그램 매칭

정의 - 스파셜 도메인 처리
스파셜 도메인 처리
-스파셜 도메인 : 이미지 평면
-스파셜 도메인 처리 : 주변 픽셀들이 변환됨(무시, 패딩)
정의 - 강도 변환
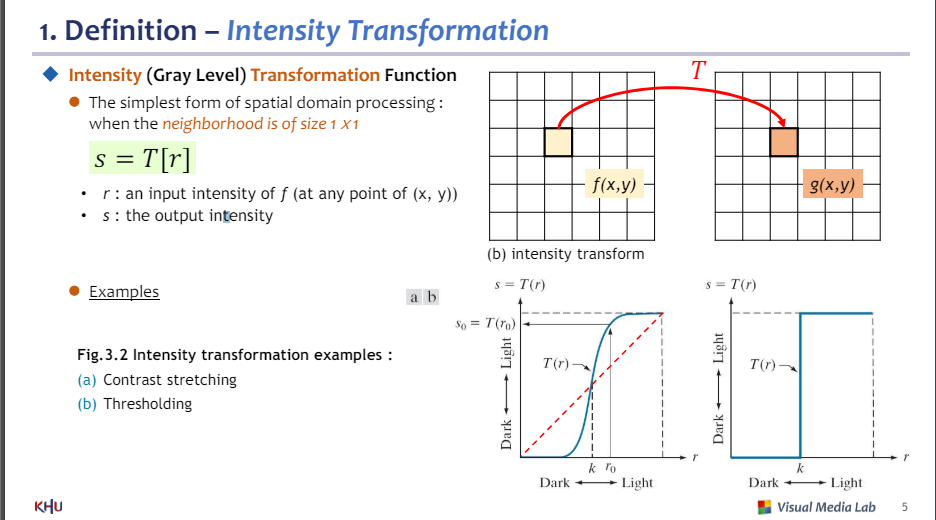
강도변환(그레이레벨) 함수
-빛의 강도를 변환함
-예제
(a) 대비 스트레칭: 대비 증가, 어두운건 더어둡고 밝은건 더밝게
(b) 스레숄딩 : 바이너리 이미지를 만듦

-포인트 처리기술이라고 불리기도함
-포인트 처리 기술 <-> 주변 처리 기술
-이미지 향상 도구임
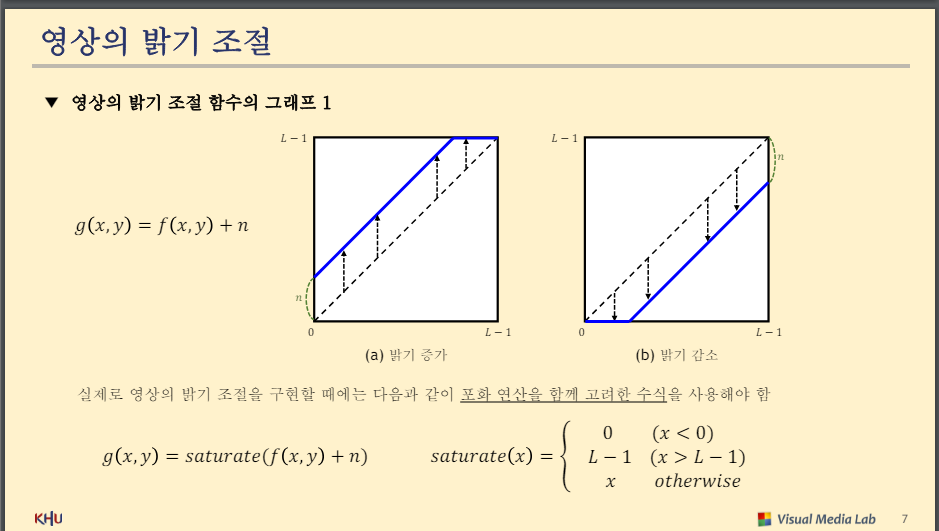
영상의 밝기 조절
포화 연산을 고려해야 함
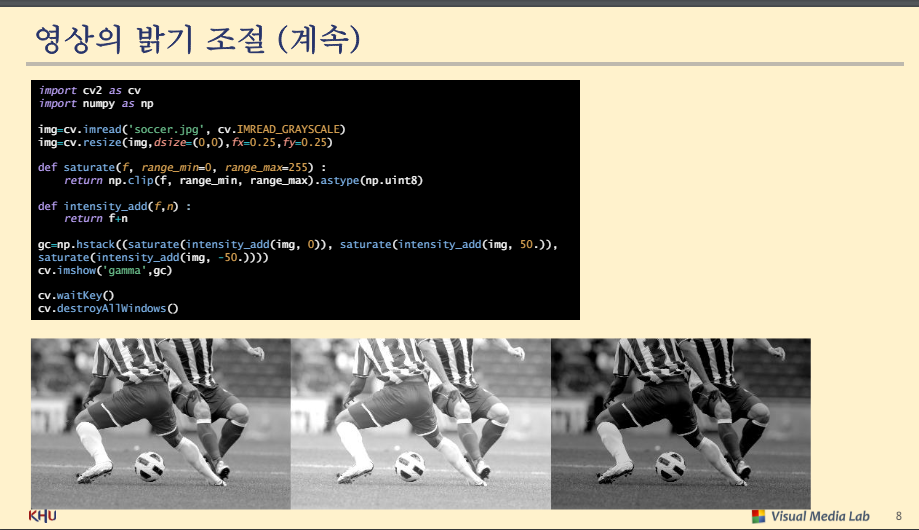
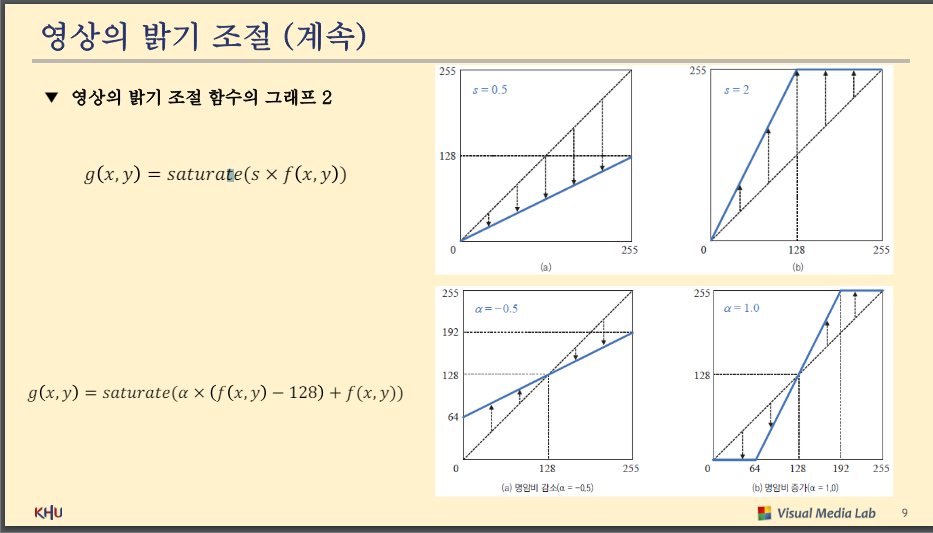
하단
(a) 명암비 감소
(b) 명암비 증가
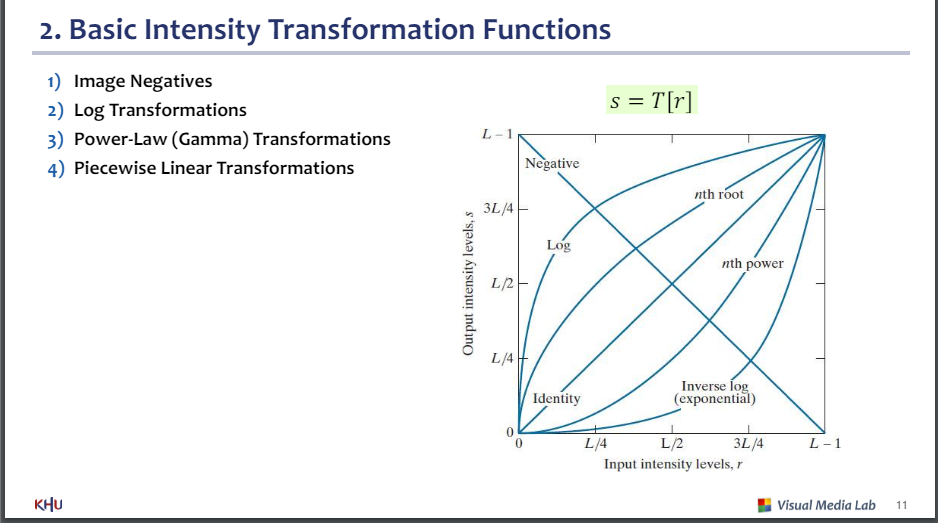
1) 이미지 음수
2) 로그변환
3) 제곱변환(감마)
4) 조각 선형 변환
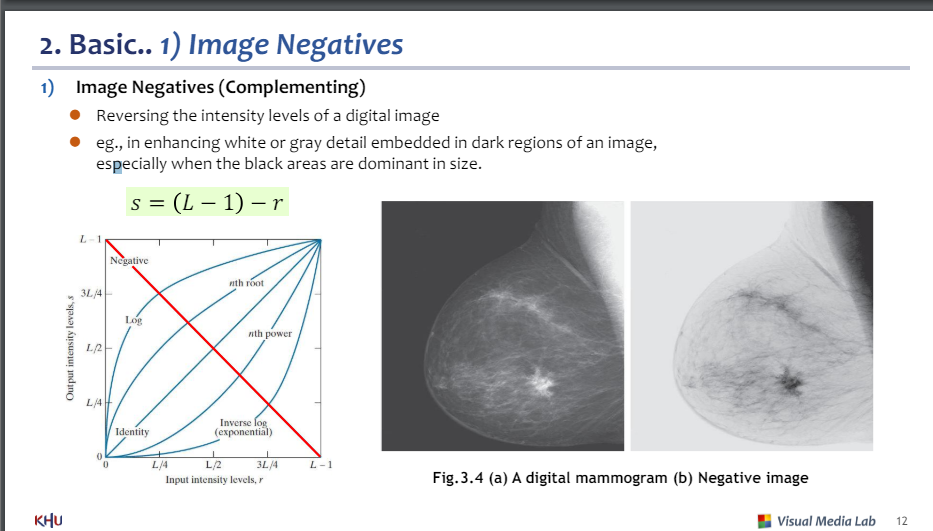
1) 이미지 네거티브
-이미지 반전
-어두운 부분이 많은 경우 사용
기울기 s = -r + (L-1)
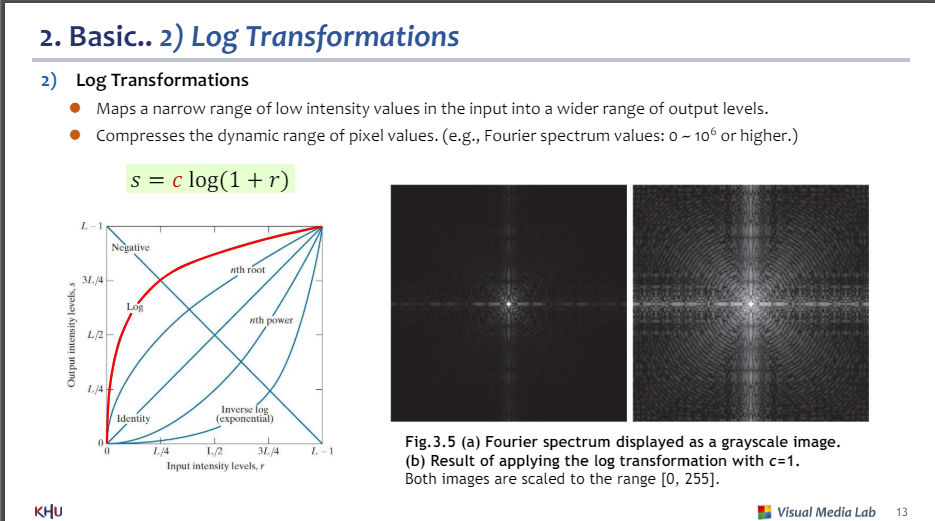
2)로그 변환
-좁은 범위를 넓은 범위의 강도 값으로 변환
-픽셀값의 다이나믹한 범위를 압축
c : 끝점을 맞추기 위함
1 + r : 시작점
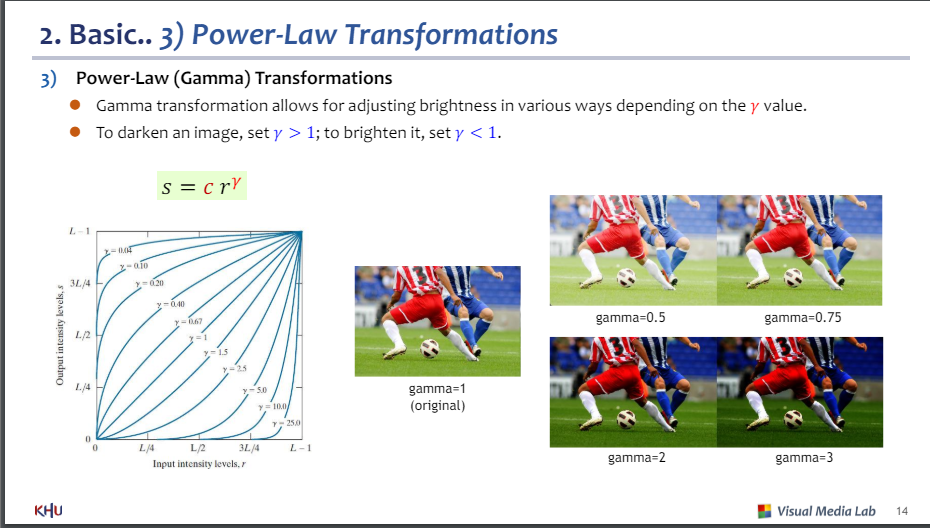
3) 제곱 변환
-감마 값에 따라 밝기를 다양하게 변환
c : 끝점
r : 1보다 크면 어두움

-이미지 디바이스가 이 방식 사용
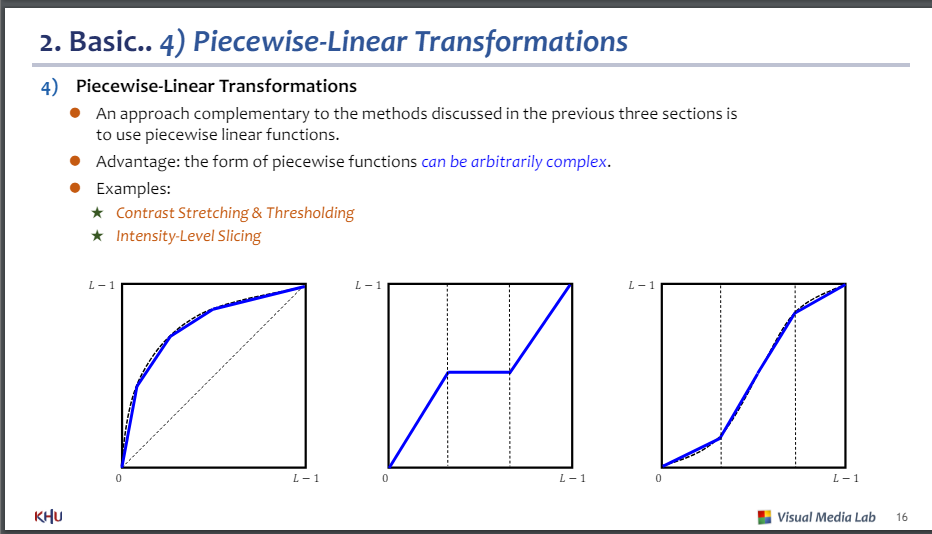
4) 조각 선형 변환
-이전 3개보다 보완적
-장점 : 임의로 구성할수 있음
예제
-대비 스트레칭 & 스레숄딩
-강도 레벨 슬라이싱
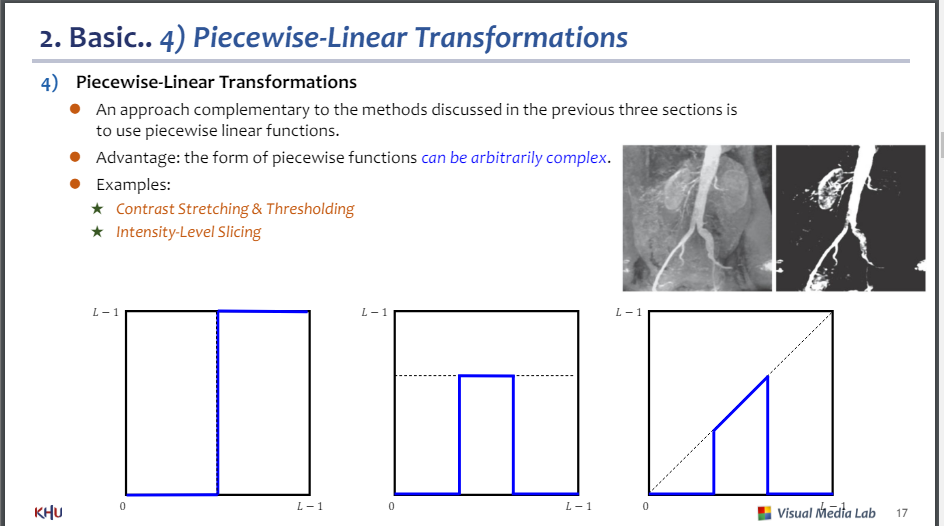
2번째 : 관심있는 영역
3번째 : 원본 그대로
 \
\
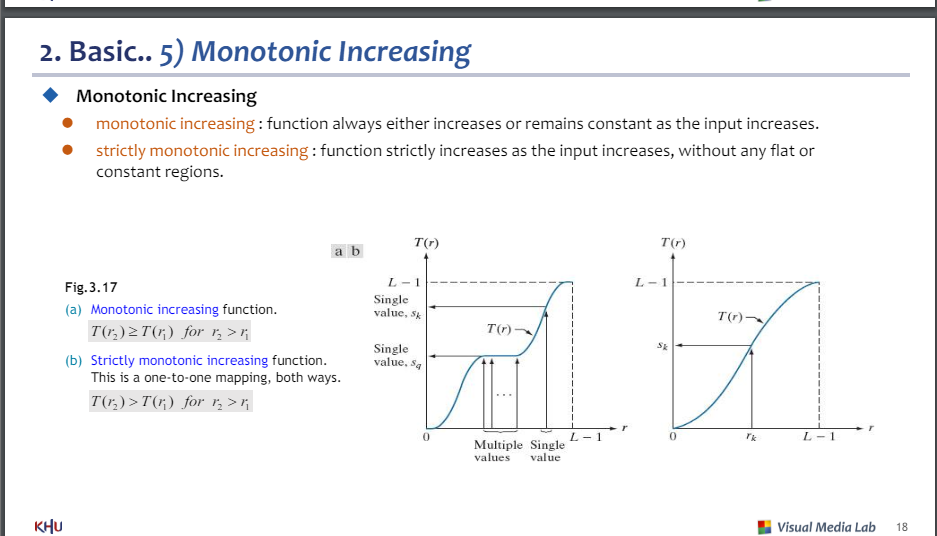
5)모노토닉 증가
-모노토닉 증가 : 함수는 유지되거나 증가만 함
-엄격 모노토닉 증가 : 증가만 함
a : 같음 허용
b : 같음 허용x
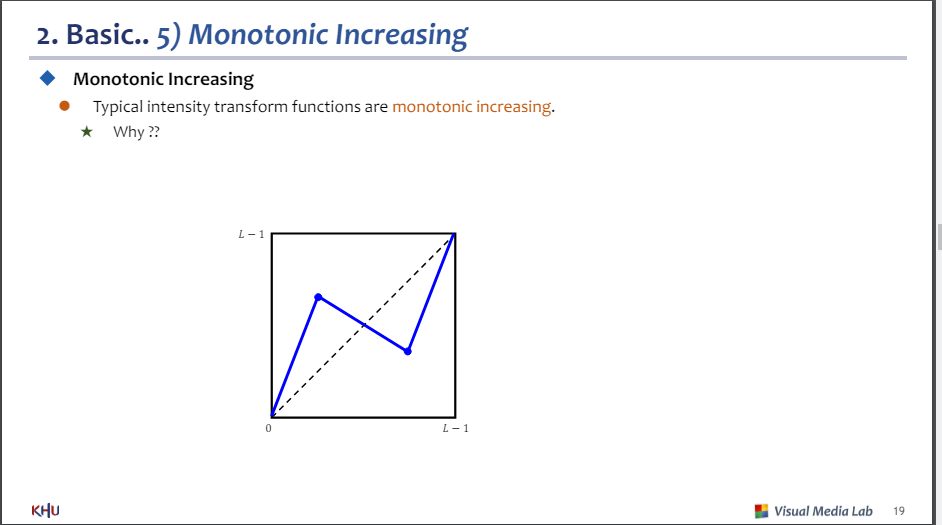
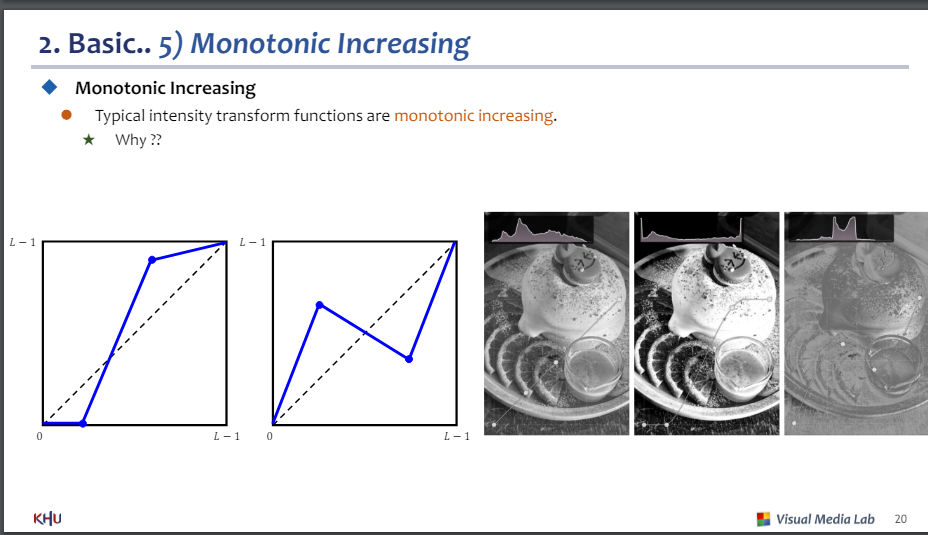
모노토닉 증가를 쓰는 이유 : 그렇지 않으면 왜곡이 심해지기 때문(명암 순서가 바뀜)


확률공간

확률 변수
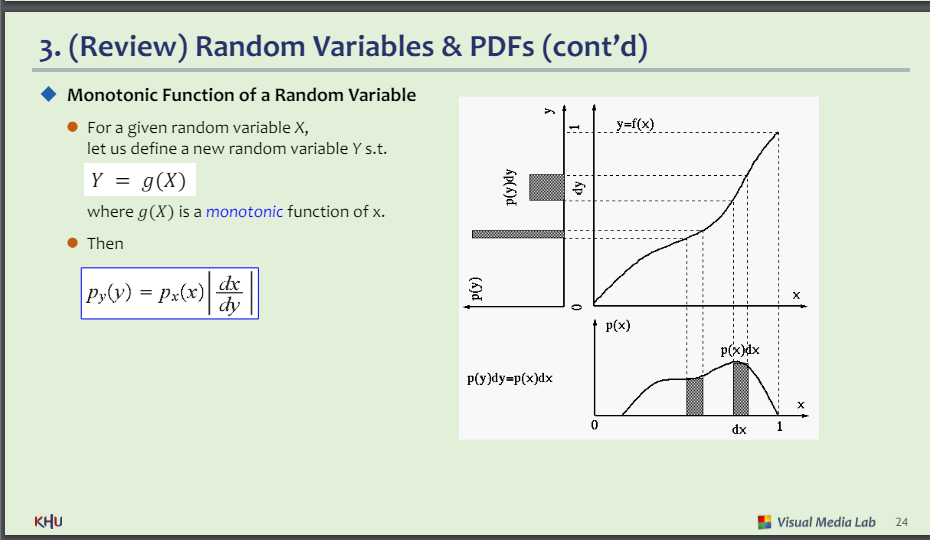
랜덤 변수의 모노토닉 함수

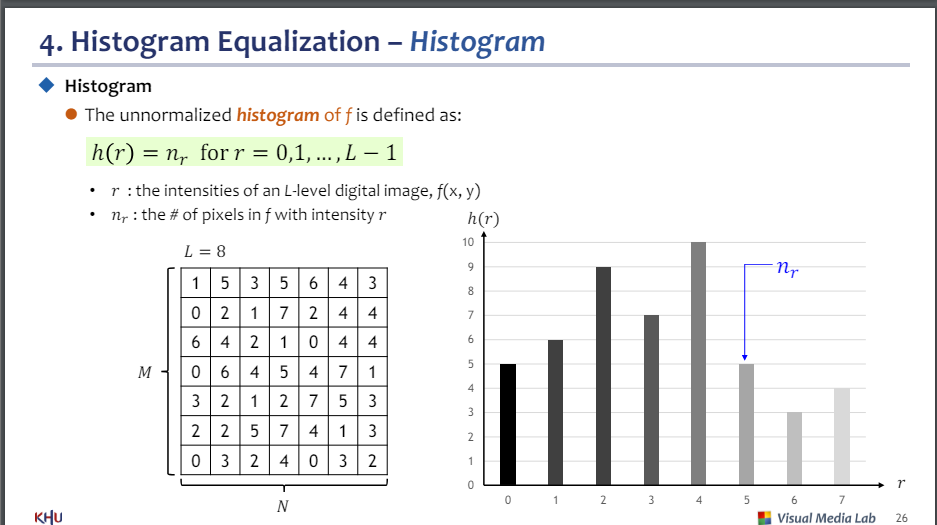
- 히스토그램 균등화
-비정규화된 히스토그램
r : 강도 값
the # : r의 개수
L = 8 : 2의 3승, 3비트
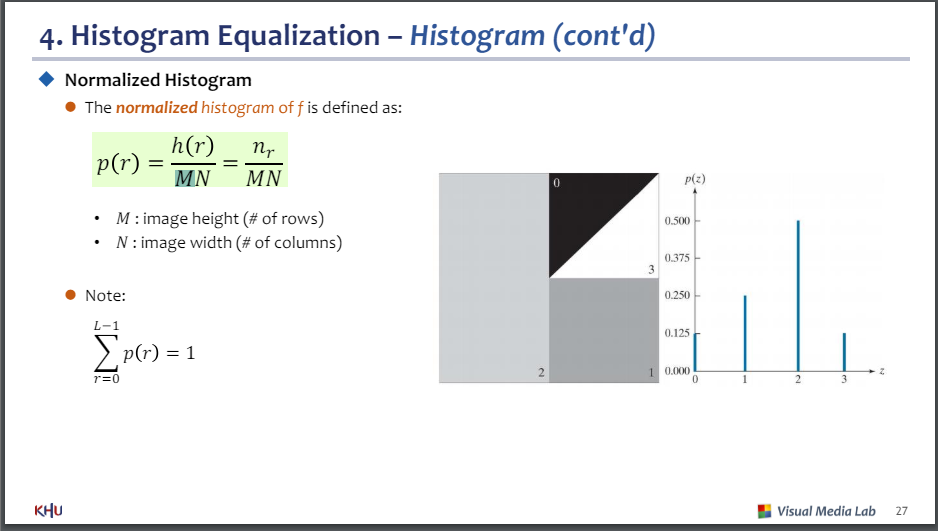
-정규화된 히스토그램
MN : 전체 픽셀 개수
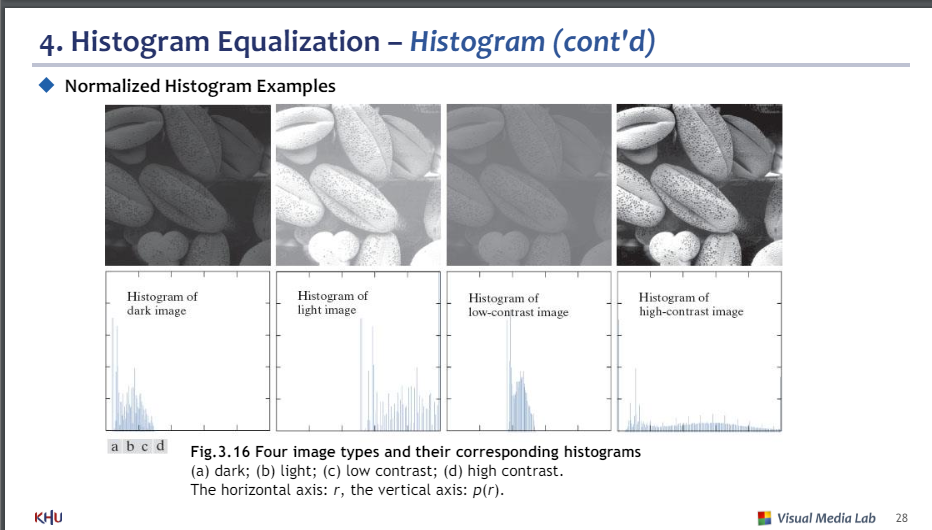
정규화된 히스토그램 예제
가로축: 밝기
세로축 : 개수
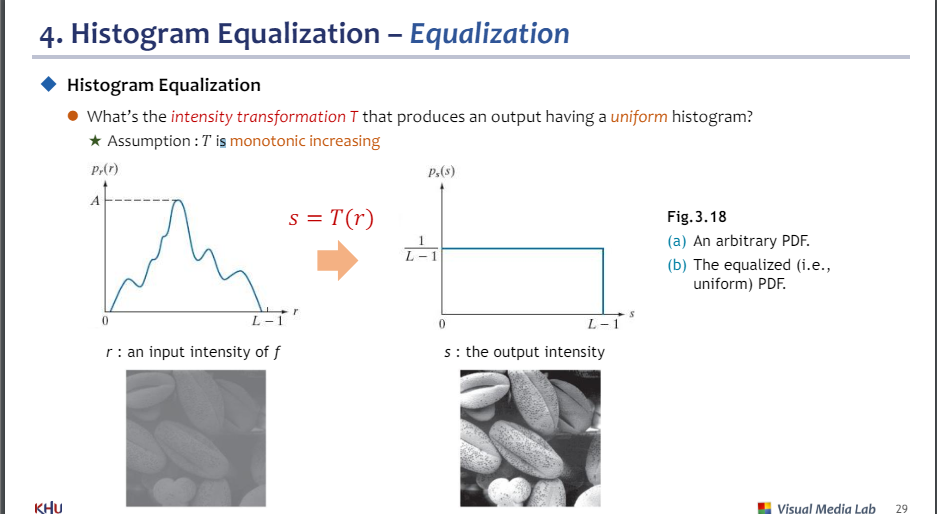
히스토그램 이퀄라이제이션 : T함수 구하기
-T함수 : 균일한 히스토그램 생성
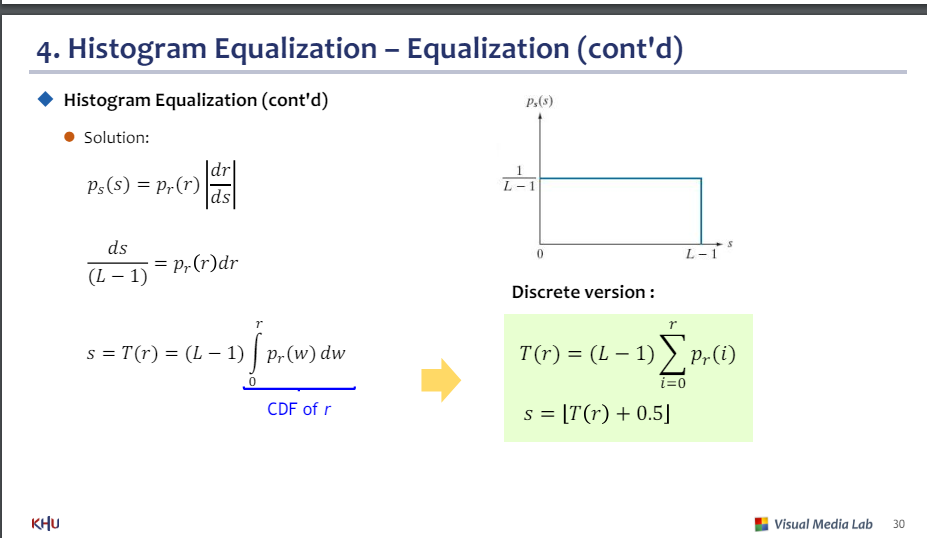
히스토그램 균일화
해결책
시험
1/(L-1) : p(s) 값
s = (L-1)*(r의CDF)
이산 버전
인티그랄은 시그마로
라운딩 연산 필요
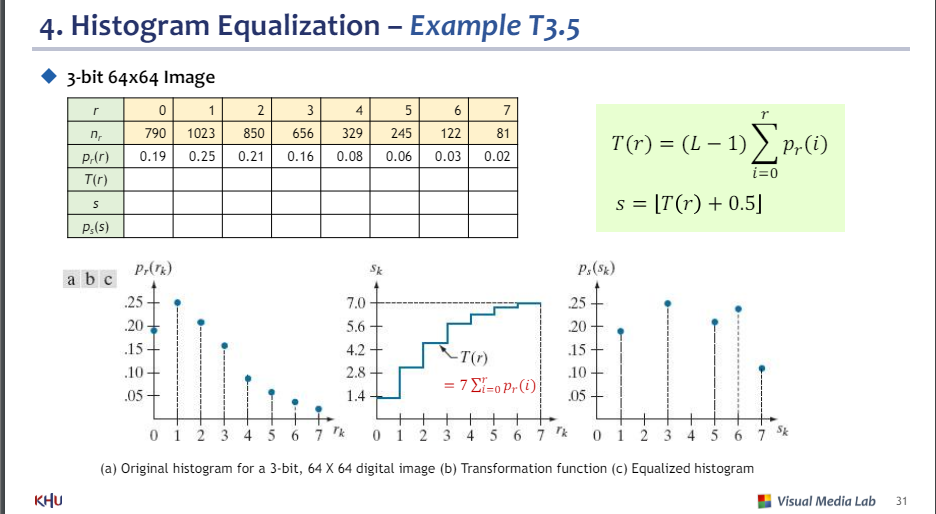
시험
빈칸 값 채우기
3비트(L=8)
p(r) : 오리지널 히스토그램에서 값 읽기(가로r 세로p(r))
T(r) : (L-1) * r의 CDF
s : T(r)에서 첫째자리 반올림, 변환 함수(가로r 세로T(r))
p(s) : s값이 같은 r들의 p(r) 합,균일화된 히스토그램(가로s 세로 p(s))
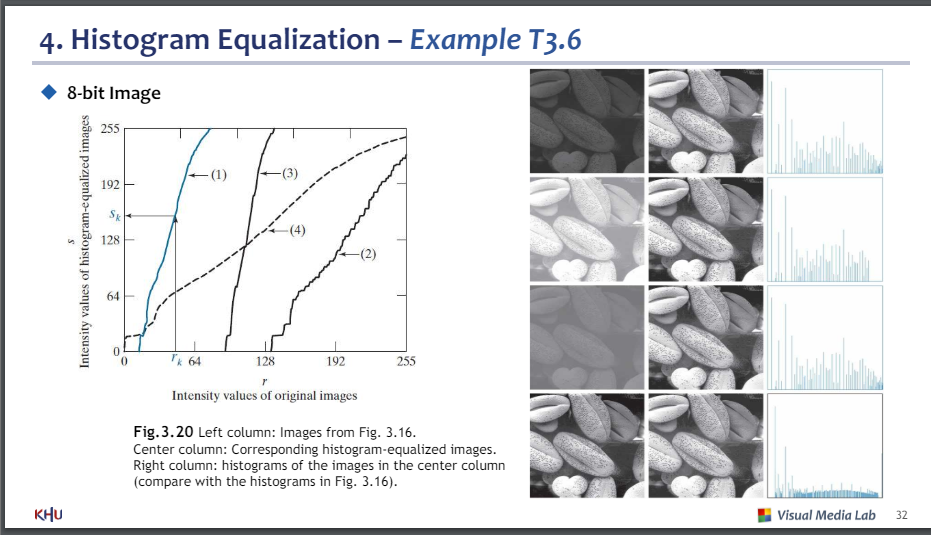
좌측열 : 이미지원본
중앙열 : 히스토그램 균일화한 이미지
오른쪽열 : 이미지의 히스토그램
위부터 1,2,3,4
가로축 : r(빛의강도)
1 : 가장 어두움
2 : 가장 밝음
3 : 중간 밝기
4 : 밝기 고루 퍼짐
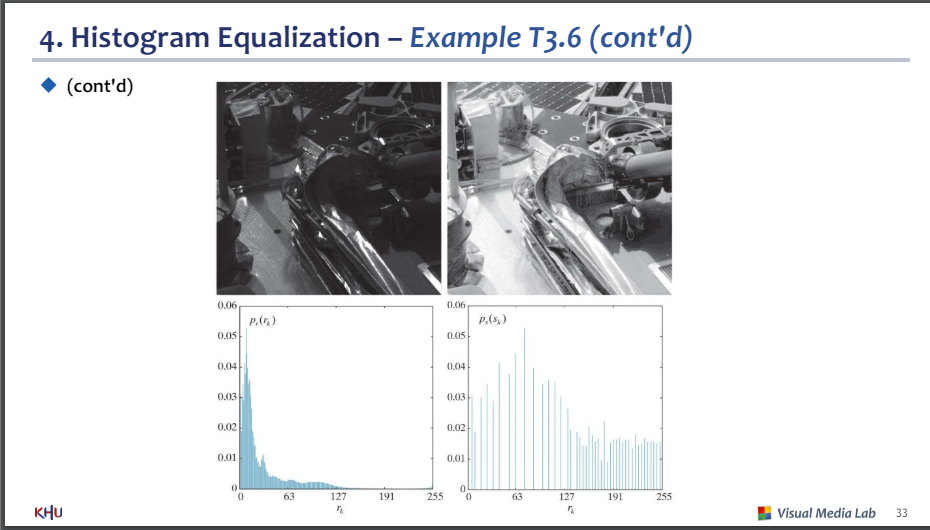
그래프가 사이사이 비어있는 이유 : 계단함수이기 때문

히스토그램 평활화
h(g) : g의 개수
H(g) : h의 CDF
H(g) * Lmax / 개수의 총합
반올림처리

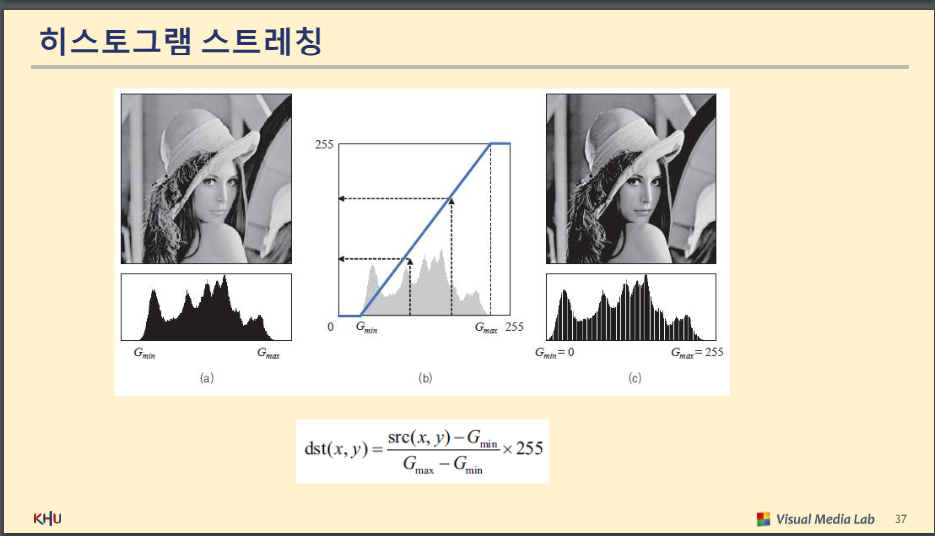
좌측 : 레인지 좁음
우측 : 레인지 넓음(레인지를 늘림)
dst(x,y)
분자 : src(x,y)인 input에서 Gmin(길이가 넘어가는 것을 방지)을 빼어 0으로 땡김
255(원하는 길이) / Gmax - Gmin(원래 길이) 곱하기: 레인지 늘어남

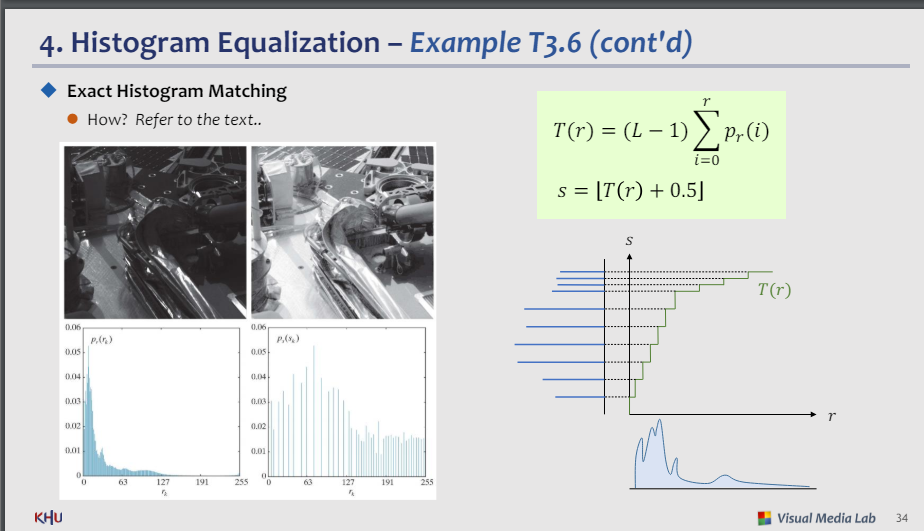
5 히스토그램 매칭
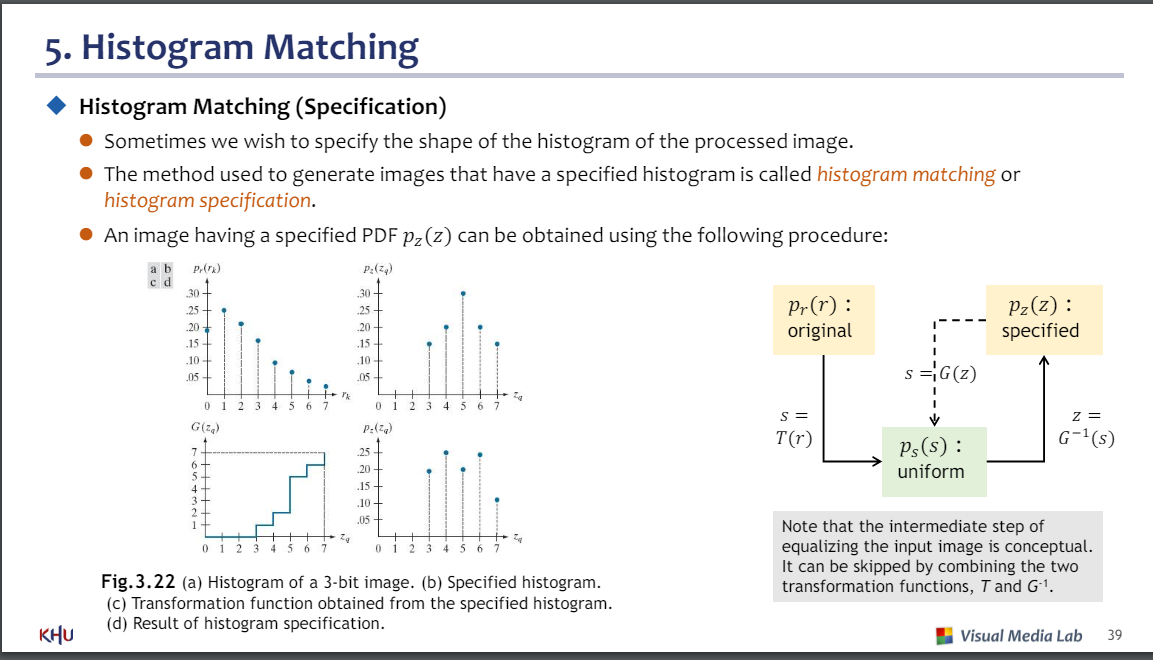
-히스토그램 매칭(구체화) : 구체화된 히스토그램을 갖는 이미지를 생성하는 방법
그림 : 오리지널 이미지를 균일화한 이후 역평활화함.
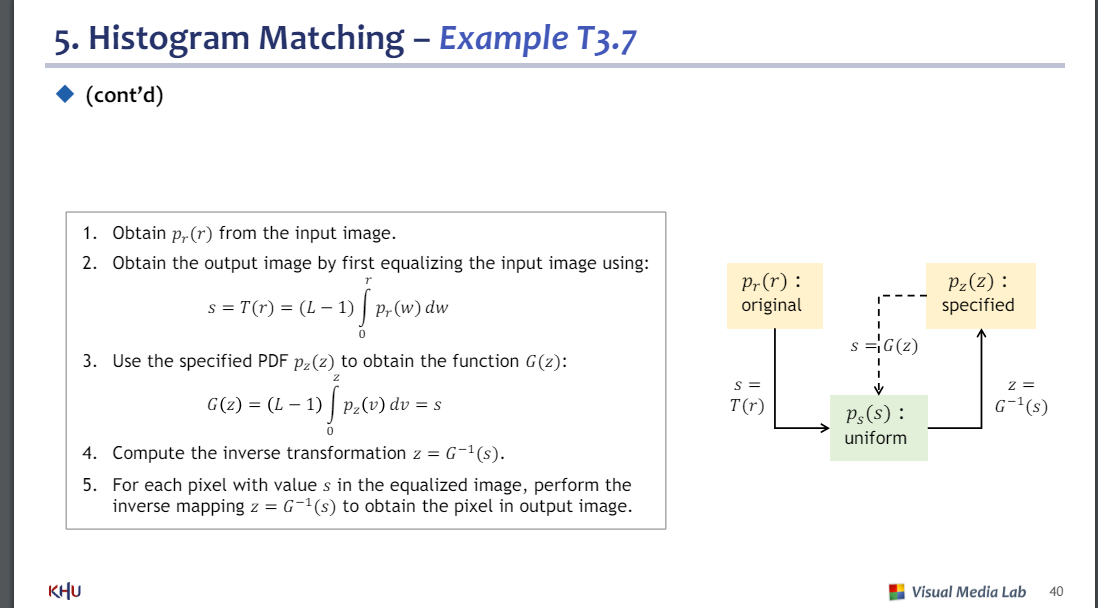
1 인풋이미지로부터 p(r) 얻기
2 인풋이미지를 균일화하기
3 G를 얻기위해 p(z)사용하기
4 G역함수 구하기
5 G역함수로 균일화하기

히스토그램 균일화 vs 매칭
히스토그램의 문제점
-어두운 영역의 내용물을 드러내는 것은 성공적
-그러나 노이즈가 많아짐

매칭
-스케일을 늘리면서, 노이즈는 적음
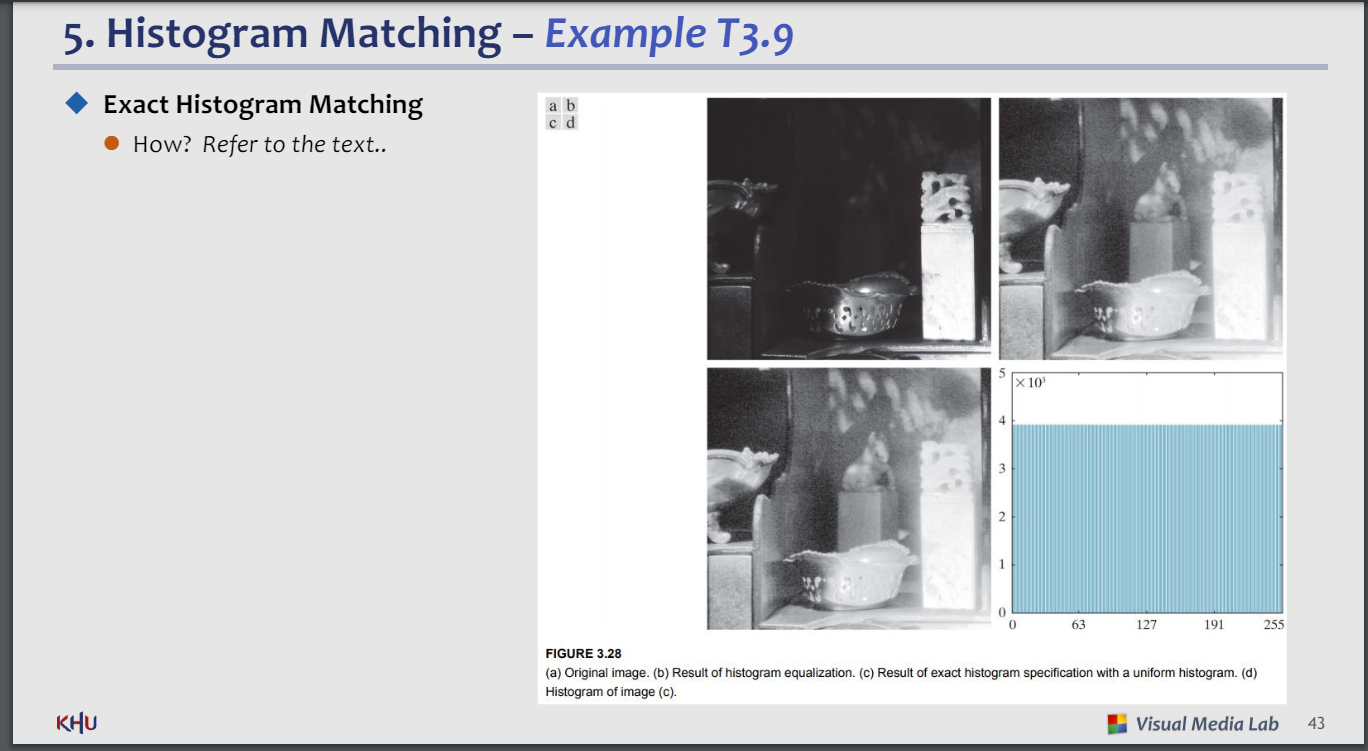
히스토그램 매칭
a)원본
b)히스토그램 균일화
c)히스토그램 매칭
b와c는 별 차이없음