

- DTFT(이산시간 푸리에 변환)
- DFT(이산 푸리에 변환)

- 샘플링 및 디지털 주파수
- 이산시간 푸리에 변환(DTFT)
- DTFT의 특성
- DTFT 쌍
- DTFT 속성 및 쌍 요약
- DTFT 연습

- Sampling & Digital Frequency 𝝎
◆ Sampling Sinusoidal Signals
◆ Digital Frequency (= Normalized Frequency)
⚫ f가 0에서 fs까지 다양하므로 0에서 2π까지 다양합니다.
⚫ 정현파는 2𝜋로 주기적입니다.

- Discrete Time Fourier Transform (DTFT)
◆ 연속시간 푸리에 변환(CTFT)
◆ 이산시간 푸리에 변환(DTFT)

- Properties of DTFT – Linearity
Linearity

◆ Conjugation
◆ Conjugate Symmetry

- Properties of DTFT – Time-/Frequency-Shift
◆ 시간지연 위상변이
◆ 시간 역전

◆ 주파수 편이(변조)

◆ Convolution


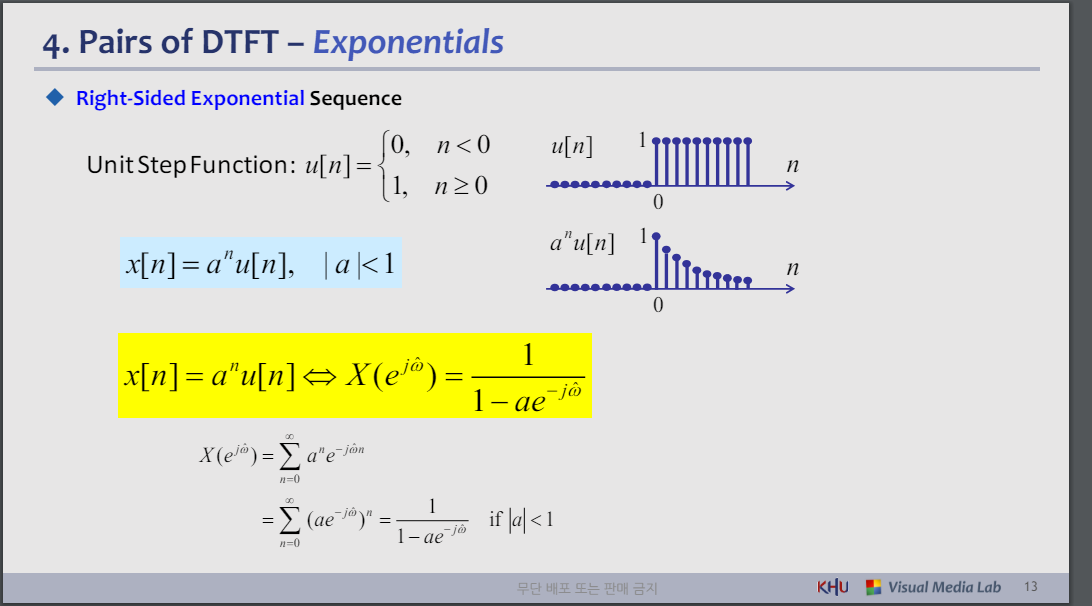
- Pairs of DTFT – Impulse
◆ 단일 샘플(단위 임펄스)
◆ 지연 임펄스

- Pairs of DTFT – Finite Rectangles
◆ L점 직사각형 펄스
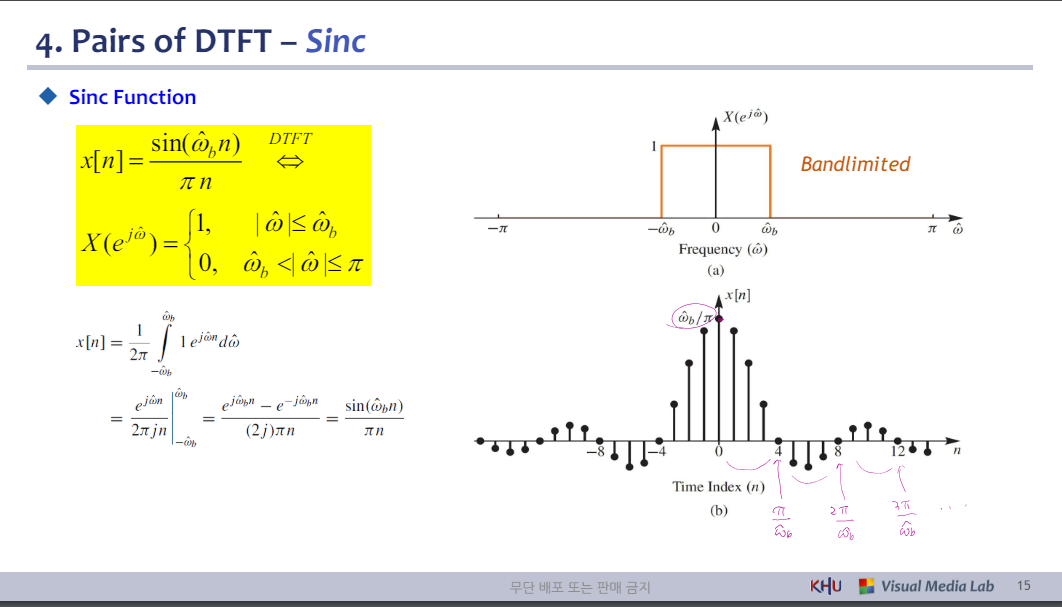
◆ Sinc Function

- Summary of DTFT Properties & Pairs





- 이산 푸리에 변환(DFT) [T.4.4]
- DFT 속성 및 쌍 [T4.4]
- FFT(고속 푸리에 변환)
- 푸리에 변환 요약

- DFT (Discrete Fourier Transform)
◆ 왜 DFT인가?
⚫ x[n]이 간단한 수학 공식으로 표현되지 않더라도 신호의 스펙트럼을 결정해야 합니다.
⚫ 즉, 우리는 신호 샘플에서 스펙트럼을 계산할 수 있는 컴퓨터 프로그램을 갖고 싶습니다.
◆ DTFT에서 DFT로
⚫ DTFT는 샘플링된 신호에 대한 푸리에 변환입니다.
⚫ 그러나 다음과 같은 이유로 컴퓨터에는 적합하지 않습니다.
★무한한 작업이 필요합니다.
★스펙트럼은 연속함수입니다.
⚫ DFT: DTFT에서 두 가지가 수정되었습니다.
★유한 신호 길이 : [-무한대, 무한대] → [0, N-1]
★ 유한한 주파수 수 :

- DFT (cont’d)
◆ N-point DFT & IDFT
⚫ DFT
⚫ IDFT
⚫ 제로 패딩
★때때로 x[n]의 시퀀스 길이 L이 N보다 짧습니다(L<N).
★이러한 경우 간단히 N−L 제로 샘플을 x[n]에 추가한 다음 N-포인트 DFT 계산을 수행할 수 있습니다.


◆ Matrix Form

2. DFT Properties & Pairs
◆ DFT & IDFT의 주기성
◆ 음의 주파수
• 시간 영역 샘플링
→ 주파수 영역의 주기성
• 주파수 영역 샘플링
→ 시간 영역의 주기성

◆ (원형) 시간 지연
시간 이동은 주기 N의 순환 이동입니다.


◆ (Circular) Convolution
⚫ DFT/IDFT 표현은 유한 길이 시퀀스를 다루기 때문에 각각 DFT 표현을 갖는 두 개의 유한 길이 신호의 컨볼루션을 연구하려고 합니다.
⚫ 따라서 컨볼루션 표현식은 아래와 같이 유한합으로 쓸 수 있습니다.
★ x[n]: 길이 L 시퀀스
★ h[n]: 길이 M 시퀀스
★ y[n]: 길이(L+M-1) 시퀀스
이제 Y를 샘플링하여 N-포인트 (N ≥ (L+M-1)) DFT Y[k]를 얻습니다.
★ 여기서는 모든 시퀀스가 N 길이로 제로 패딩되었다고 가정했습니다.
⚫ 고유한 주기성으로 인해 Y[k]=H[k]X[k]는 다음과 같이 고유한 주기 시퀀스 𝑥[𝑛] 및 𝑥[𝑛]의 주기(원형) 컨볼루션을 나타냅니다.


- DFT 속성 및 쌍(계속)

◆ DTFT Pairs ◆ DFT Pairs

- FFT (Fast Fourier Transform)
◆ FFT는 DFT를 빠르게 계산하기 위한 알고리즘입니다.
⚫ 계산 결과는 동일합니다.
◆얼마나 빨라졌나요?
⚫ 계산 복잡성: N2 대 N log2N 작업.
★ 곱셈(및 덧셈) 횟수를 세어보세요.
★ 예) N=1024 : 10,000 ops vs. 1,000,000 ops → 1000배 빨라진다!

