
1. 이미지 복원 모델
2. 복원을 위한 성과조치
3. 열화 추정(T5.6)
4. 역 필터링(T5.7)
5. 위너 필터링(T5.8)
6. 제한된 최소제곱 필터링(T5.9)
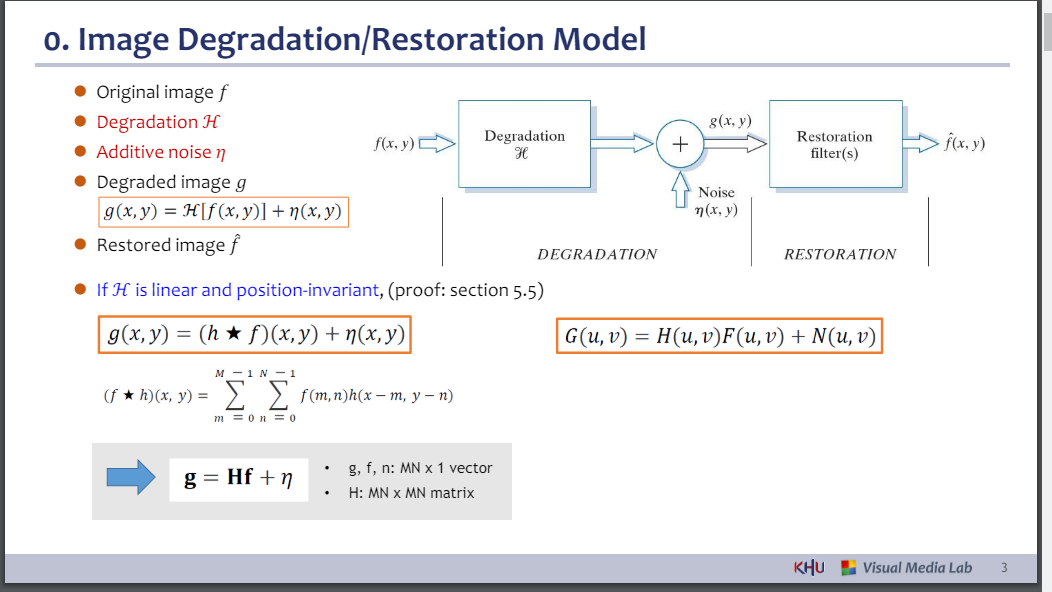
- 이미지 저하/복원 모델
⚫ 원본 이미지 𝑓
⚫ 저하 ℋ
⚫ 부가적인 소음 𝜂
⚫ 저하된 이미지 𝑔
⚫ 복원된 이미지 𝑓መ
⚫ ℋ가 선형이고 위치 불변인 경우 (증명: 섹션 5.5)



- 복원을 위한 성과조치
◆ MSE(평균제곱오차)
◆ SNR(신호 대 잡음비)
⚫ 주파수 영역 근사
⚫ 공간 영역 근사
◆ PSNR(피크 신호 대 잡음비)
⚫ 신호 값 대신 피크 신호 값을 사용하십시오.

◆ 때로는 앞의 두 측정값(예: MSE 및 SNR)의 제곱근이 대신 사용됩니다.
⚫ MSE와 SNR은 '전력'의 비율입니다.
⚫ RMSE(루트 MSE) 및 RSNR(루트 SNR)은 값 자체의 비율입니다.
◆ 로그 스케일의 SNR 및 PSNR
⚫ 대부분 SNR과 PSNR은 로그 스케일(dB)로 측정됩니다.
⚫ SNR
⚫ PSNR

- 성능 저하 추정(𝓗)
◆ 복원을 위해서는 열화기능𝓗을 알아야 합니다.
⚫ 그렇다면 𝓗를 찾는 방법은 무엇일까요?
◆ 3가지 주요 방법
A. 저하에 대한 통찰력이 있는 경우(예: 난기류, 모션 등)
→ 𝓗의 수학적 모델링을 시도해 보세요.
나. 열화영상 획득에 사용되는 유사한 장비(예: 카메라)가 있는 경우
→ 장비의 임펄스 응답을 얻기 위해 실험을 해보세요.
다. 통찰력이나 장비가 없는 경우
→ 이미지 관찰을 시도합니다. (즉, 저하된 이미지 자체에서 직접 정보를 수집합니다.)

2. 성능 저하 추정 – A. 수학적 모델링
A. 수학적 모델링에 의한 추정
1) 예: 대기 난류(대기난류)
★ 어떤 경우에는 모델이 성능 저하를 일으키는 환경 조건을 고려할 수도 있습니다.

A. 수학적 모델링에 의한 추정(계속)
2) 예: 모션 블러
★ 모델링에 자주 사용되는 또 다른 접근법은 기본 원리에서 출발하여 수학적 모델을 도출하는 것입니다.
▪ 영상 획득 시 영상과 센서 사이의 움직임으로 인해 영상이 흐릿해졌습니다.
▪ 이미징 시스템 셔터가 열려 있는 동안 시간 간격 T에 걸쳐 순간 노출을 통합하여 기록 매체(예: 필름 또는 디지털 메모리)의 모든 지점에서 총 노출을 얻습니다.
★ 영상 f(x, y)가 평면 운동(평면 운동)을 한다고 가정

A. 수학적 모델링에 의한 추정(계속)
⚫ 예: 모션 블러(계속)
★ 추가적으로 등속 아름다운 운동을 가정합니다.
▪ 사례 1: x 방향으로만 일정한 속도(예: 𝑥0 𝑡 = 𝑎𝑡/𝑇, 𝑦0 𝑡 = 0)
▪ 사례 2: x 방향과 y 방향 모두에서 일정한 운동을 허용하는 경우
(예: 𝑥0 𝑡 = 𝑎𝑡/𝑇 및 𝑦0 𝑡 = 𝑏𝑡/𝑇),
• PxQ 크기의 이산 필터 전달 함수를 생성하기 위해 u=0,1,..,P-1 및 v=0,1,…,Q-1에 대해 이 방정식을 샘플링합니다.
• H(u, v)의 중심 버전은 H(u-P/2, v-Q/2)입니다.

- 열화 추정 – B. 실험
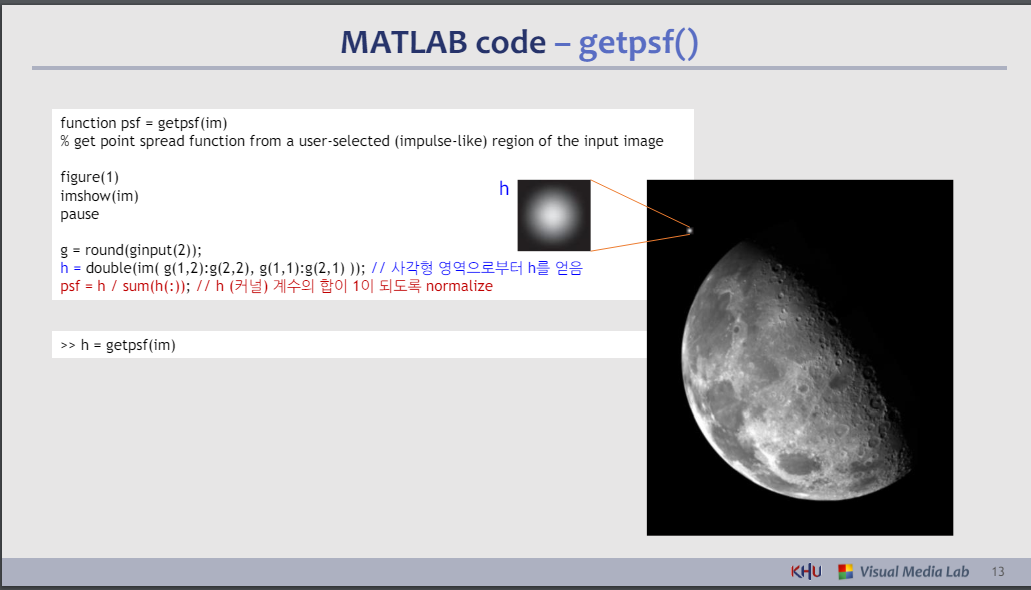
B. 실험에 의한 추정(충동응답)
⚫ 조건 : 열화영상 획득에 사용된 장비와 유사한 장비가 있어야 합니다.
⚫ 아이디어: 동일한 시스템 설정을 사용하여 임펄스를 이미징하여 열화의 임펄스 응답을 얻습니다.
★ 이상적으로는 𝑓 𝑥, 𝑦 = 𝛿(𝑥, 𝑦)인 경우 𝜂 𝑥, 𝑦 = 0, 𝑔 𝑥, 𝑦 = ℎ(𝑥, 𝑦)이라고 가정합니다.
★ 임펄스는 노이즈 효과를 줄이기 위해 최대한 밝은 밝은 점으로 시뮬레이션됩니다.
▪ 시뮬레이션된 충격 강도가 𝐴이면 ℎ 𝑥, 𝑦 = 𝑔(𝑥, 𝑦)/𝐴입니다.
▪ 또한 𝐻 𝑢, 𝑣 = 𝐺(𝑥, 𝑦)/𝐴에 의해 임펄스 응답을 푸리에 변환할 수 있습니다.

2. 열화 추정 – C. 이미지 관찰
영상 관찰에 의한 추정(Guessing)
⚫ 저하 함수 ℋ에 대한 지식 없이 저하된 이미지가 제공되었다고 가정합니다(LSI 가정 제외). 그런 다음 저하된 이미지𝑔에서 직접 정보를 수집해야 합니다.
⚫ 절차:
1) 무시할 수 있는 노이즈 영역(즉, 고대비 영역과 같은 강한 신호 콘텐츠)을 식별합니다: 𝑔𝑠(𝑥, 𝑦).
▪ 일반적으로 물체의 일부 및 배경과 같은 단순한 구조를 포함하는 이미지의 작은 부분입니다.
2) 하위 이미지를 처리하여 𝑓መ 𝑠(𝑥, 𝑦)을 얻습니다.
3) 디콘볼루션을 통해 하위 이미지의 저하 함수를 추정합니다. 𝐻𝑠 𝑢, 𝑣 = 𝐺𝑠(𝑢, 𝑣)Τ𝐹 𝑠(𝑢, 𝑣).
4) 𝐻𝑠 𝑢, 𝑣의 정보를 활용하여 𝐻 𝑢, 𝑣를 대규모로 구성합니다.

3. 역필터링을 통한 복원
◆ 우리가 저하 함수 ℋ를 알고 있다고 가정합니다. 그렇다면 ℋ를 사용하여 이미지를 "복원"하는 방법은 무엇입니까?
◆ 역 필터링 – 가장 간단한 접근 방식
⚫ 소음 없이 아주 잘 작동합니다.
⚫ 소음이 있으면 뭔가 나쁜 일이 발생합니다.
★ H(u,v)의 값이 0이거나 매우 작은 경우 N(u,v)/H(u,v) 비율이 F(u,v) 항을 쉽게 지배할 수 있습니다.
⚫ 이 작은 값 문제를 해결하기 위한 접근 방식: 큰 H(u,v) 값만 사용하세요!
★ 필터 주파수(u,v)를 원점에 가까운 값(즉, 낮은 주파수)으로 제한합니다.
★ H(u,v)는 일반적으로 원점(0,0) 근처에서 높은 값을 가집니다.
★ 예: 다음 슬라이드..

◆ 예: 역필터링을 통한 이미지 디블러링
⚫ 저하 기능(대기 난류):

4. 위너 필터링을 통한 복원
◆ 노이즈의 열화함수와 통계적 특성을 모두 통합한 접근 방식입니다.
⚫ 이미지와 노이즈를 확률변수로 생각하고 통계적 추정이론을 활용해보자.
◆ 가정
⚫ 노이즈와 이미지는 서로 관련이 없습니다.
◆ 목표: MSE 최소화
⚫ 둘 사이의 MSE(평균 제곱 오차)가 최소화되도록 손상되지 않은 𝑓의 추정치 𝑓መ를 찾습니다.

◆ The Result (MMSE Estimator)
우리는 Sf(u,v)를 추정할 수 있습니다. 예를 들어, 백색 잡음의 스펙트럼 N(u,v)는 상수입니다.
그러나 품질 저하되지 않은 이미지의 전력 스펙트럼 Sf(u,v)는 거의 알려져 있지 않습니다.
이러한 양을 알 수 없는 경우 잡음 대 신호 전력 비율 대신 조정 가능한 매개변수 K가 사용됩니다.


◆ 예 5.10: 역필터링과 Wiener 필터링에 의한 디블러링 비교

◆ 예 5.11: Wiener 필터링을 사용한 추가 디블러링 예

5. 제한된 최소제곱 필터링을 통한 복원
◆ 위너 필터 사용의 어려움
⚫ 품질 저하되지 않은 이미지와 노이즈의 파워 스펙트럼을 알아야 합니다.
⚫ 어떤 경우에는 식의 근사를 사용하여 수용 가능한 결과를 얻는 것이 가능합니다. (5-85), 그러나 전력 스펙트럼 비율(즉, K)에 대한 일정한 값이 항상 적합한 솔루션은 아닙니다.
◆ 제한된 최소제곱 필터링
⚫ 노이즈의 평균과 분산만 필요합니다.
★ 섹션 5.2에서 설명한 대로 이러한 매개변수는 일반적으로 주어진 저하된 이미지에서 계산할 수 있습니다.



- 제한된 최소제곱 필터링을 통한 복원(계속)

그림 5.31(a) 올바른 노이즈 매개변수를 사용하여 그림 5.25(b)의 제한된 최소 제곱 복원을 반복적으로 결정합니다. (b) 잘못된 노이즈 매개변수로 얻은 결과.