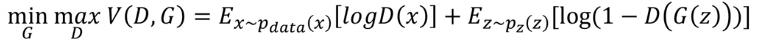GAN : Generative Adversarial Nets

0. GAN 핵심 요약

• GAN?
  실제로 존재하지는 않지만, 있을법한 데이터를 만들 수 있는 생성모델 중 하나입니다.

• 확률 분포를 이용(학습)
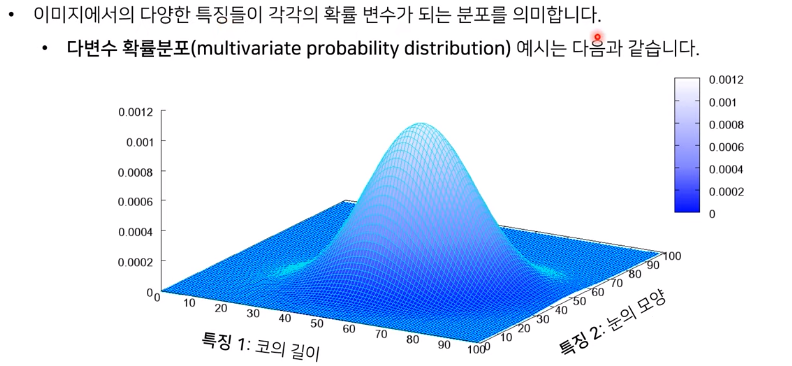
  키와 아이큐 같은 데이터는 1차원으로 표현될 수 있지만, 이미지 데이터는 많은 픽셀들로 구성되어 있고, 각 픽셀들 또한 RGB로 3개의 채널을 가지고 있기 때문에 다차원 특징 공간의 한 점으로 표현됩니다. 그렇기에 이미지의 분포를 근사하는 모델을 학습할 수 있습니다.
  (사람의 얼굴에는 통계적인 평균치가 존재할 수 있습니다.(눈의 길이, 코의 길이, 두께 등) 모델은 이를 수치적으로 표현하게 됩니다.)
  

• 생성 모델은 무엇인가? (Generative Model)
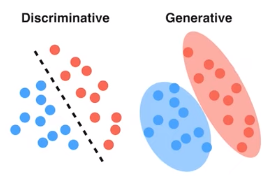
  우선 Generative model vs Discriminative model 을 참고하시면 좋습니다.

• Discriminative : Decision boundary를 학습
• Generative : class의 분포를 학습
  

생성 모델은 실존하지는 않지만 있을 법한 이미지, 자연어 문장, 오디오 등을 생성할 수 있는 모델을 의미합니다.
여러 개의 변수에 대한 joint probability distribution 형태로 통계적인 모델로 표현하며, 새로운 data instances를 생성합니다.

* instance?) 사진 한 장과 같은 구별되는 데이터 객체

확률 분포를 잘 학습할 수 있다면, 그 모델은 통계적인 평균치를 내제할 수 있습니다.

분포를 잘 학습한 뒤에, 확률이 높은 곳에서 부터 출발해서 약간의 노이즈 섞어가며 랜덤 샘플링을 진행한다면, 그렇게 만들어진 이미지는 굉장히 다양한 형태로 그럴싸한 이미지를 만들어낼 것입니다.

즉, 이미지 데이터의 분포를 근사하는 모델 G를 만드는 것이 생성 모델의 목표
: 모델 G가 잘 작동한다는 의미는 원래 이미지들의 분포를 잘 모델링할 수 있다는 것

• Generativ Adversarial Networks : GAN
  GAN은 두 개의 네트워크 생성자(G)와 판별자(D)를 활용한 생성 모델입니다.
  학습 이후에는 생성자를 이용하게 되면, 판별자는 생성자가 학습을 잘 할 수 있게 도와주는 목적을 가집니다.

목적함수는 이와 같으며
V라는 값을 생성자는 낮추려고 노력하고, 판별자는 높이려고 노력합니다.
V는 두 개의 항으로 구성되어 있으며,
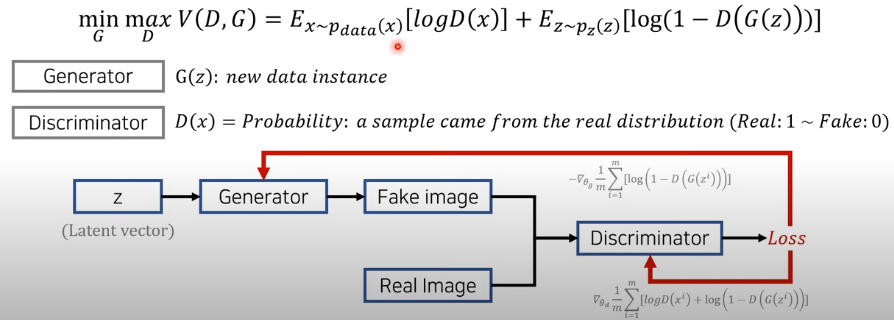
왼쪽 - Pdata 원본 데이터의 확률분포 이며, 원본 데이터의 확률분포에서 임의의 x를 샘플링하여 꺼내겠다.(쉽게 말하면, 이미지 데이터 셋에서 하나를 꺼내 D에 넣겠다.) 그리고 log를 씌운 평균값을 구하겠다.
=> 여러개의 데이터를 꺼내서 D에 넣고 log를 씌우고 평균을 구하겠다. 이를 통해 원본 데이터는 1에 가깝게 지속적 학습을 진행하게 된다.
오른쪽 - 생성자에 대한 개념이 포함되어 있으며 , 생성자는 노이즈를 포함한 벡터를 받아 이미지를 만들게 되는데, p(z)는 노이즈를 포함한 데이터셋의 distribution이며, 여기서 노이즈 벡터 z를 샘플링하여 식에 대입한다.
=> 노이즈를 포함한 데이터셋 분포에서 여러개를 꺼내어 생성자를 통해 이미지를 생성하고 이를 판별자에 넣은 후 1에서 빼고 log를 씌운 후 평균값을 구한다.

D(G(z))가 1에 가깝다는 것은 이미지를 원본 데이터셋과 유사하게 만들었다는 것이며, V값은 낮아지게 됩니다. 그렇기에 생성자 G의 목표는 V를 낮추는 것이며, 판별자 D는 V를 높이는 것이 각자의 목표인 것입니다!

그렇기에 왼쪽 식은 판별자만 보게됩니다. 생성자는 오른쪽 텀만 보며 이를 최대한 낮추기 위해 진행합니다.
회색 글씨로 이루어진 식을 보면 이는 각각에 대한 손실함수입니다.
학습을 진행할 때, D를 먼저 학습하고 G를 학습하거나, G를 먼저 학습하고 D를 학습하는 방식을 진행하는데 매번 mini batch마다 변경합니다. 이를 통해 각각이 optimal한 point로 잘 이동할 수 있게 학습을 진행합니다.

• 기댓값이 나오는데 기댓값을 구하는 방법

  • 이산확률 변수 : E[x] = sigma(xi*f(xi))
  • 연속확률 변수 : E[x] = integral(x*f(x))dx
    where x:사건, f(x):확률분포함수

• GAN의 공식의 목표
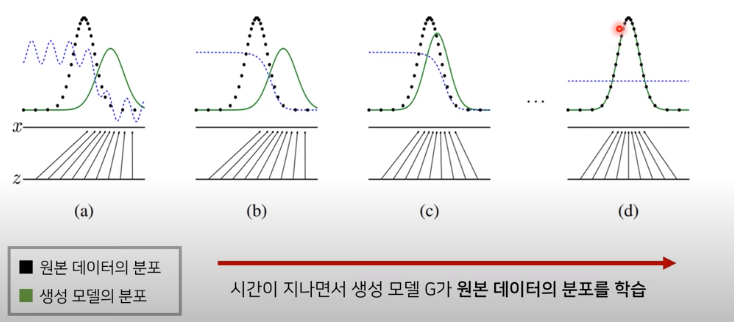
  Pg -> Pdata 로 수렴하게 만드는 것!(즉, 생성 이미지들의 분포가 원본 이미지들의 분포와 유사하게 만드는 것) 이는 다시 말해서 판별자가 구별할 수 없게, 판별자의 값이 1/2로 찍을 수 밖에 없게 만드는 것 입니다.
  
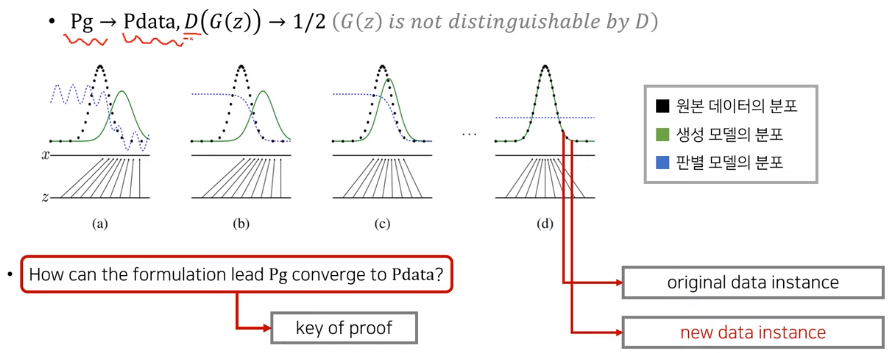
  그림을 보시면 z의 도메인에서 x의 도메인으로 매핑이 이루어지는데 원본의 x들의 distribution을 잘 만들 수 있게 매핑이 되는가! 이렇게 만드는 것이 목표입니다. 그렇게 된다면 판별 모델은 1/2로 값이 나올 수 밖에 없게 됩니다.

• 두 가지 증명 : Global Optimality ① & ②
  매 상황에 대해서 생성자와 판별자가 각각 어떤 포인트로 global optimal을 가지게 되는가에 대한 증명입니다.

  • Proof 1) 판별자의 Global Optimality ①
    
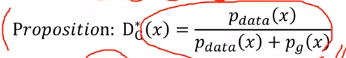
    판별자 D 의 optimal point는 위 D star 와 같습니다.
    (생성자 G는 고정되어 있습니다.)
    이에 대한 증명을 진행하겠습니다.
    
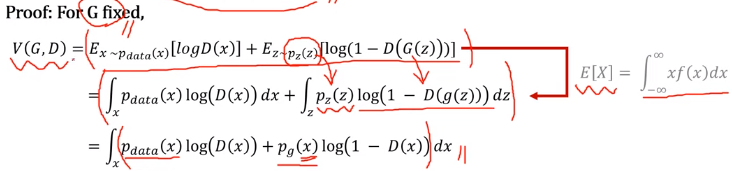
    pf① ) V를 이전에 말한 식으로 놓고, 연속확률분포의 E(X)를 이용하여 식을 재구성합니다. 이후 g(z)자체가 결국 x를 만들기 위함이고 x와 매우 유사하게 만들었다면 g(z)를 x로 설정하여 식을 다시 구성합니다. 이렇게 만들어진 식을 미분하여 극대값을 구하게 된다면, 최종 maximum point in [0,1] = D* 가 되게 됩니다.
    (혹은 아래와 같이 식을 생각하여 미분 없이(물론 미분으로 나온 식이지만) 도출할 수 있습니다.)
    
  • Proof 1) 생성자의 Global Optimality ②
    
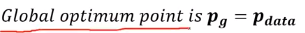
    궁극적으로 알고 싶은 생성자의 gloabla optimal point로 이는 Pg = Pdata (학습을 진행할 수록 생성자의 분포 = 원본 데이터 를 따라가게 된다) 와 같습니다.
    
    pf② ) 여기서는 별도의 함수 C를 구성하게 되는데 이 C는 D에 대한 V값을 maximize하는 식입니다.(특정 fixed G함수에 대한 global optimal을 갖는 D star를 이용한 V)
    이 식은 pf①에서 증명한 D start를 이용하여 식을 재구성하고 log(4)를 이용하여 증명을 쉽게 하기 위해 식을 재정비합니다. 이 이유로는 이 식을 KL Divergence(쿨백 레이블러 발산)로 바꾸기 위함인데 KL Divergence는 두 개의 확률분포(Pg와 Pdata)가 얼마나 차이가 나는지에 대해 수치적으로 표현하는 기법입니다. 이를 통해 두 분포의 기댓값과 각 Pdata, Pg의 차이를 KL 발산으로 표현하고, jensen shannon divergence(두 분포의 distance를 표현)를 이용하여 이를 최종적으로 표현해주게 됩니다.(KL발산은 distance metric으로 표현하기 어렵기 때문에, JSD를 이용하여 distance metric으로 효과적인 표현이 가능합니다.)
    즉, 이 JSD를 최소화하는 것이 목표이며, Pg = Pdata 일때 JSD가 0이 되기에 최종적인 생성자 G의 global optimal point Pg = Pdata가 되게 됩니다.
    생성자는 D가 이미 잘 수렴해서 global optimal D star를 가지고 있다고 가정한 상태에서 생성자가 잘 학습해서 Pg = Pdata와 같이 같은 분포를 가질 수 있도록 수렴하게 됩니다!
    (물론 이 두 proof는 학습이 잘 되어서 global optimal을 찾을 수 있다는 가정 하에 증명된 것이며, global opitmal에 잘 들어갈 수 있는가에 대한 내용은 엄밀히 다르게 다루어져야 하는 내용입니다.)
    (GAN은 학습시키기 까다로운 모델이기도 하며, 차후 다른 논문들에 이를 안정화시키기 위한 다양한 내용들이 등장합니다.)

GAN의 목적함수를 알아봤고, 이 목적함수로 학습을 진행했을 때 global optimal point가 어디인지 또한 알아봤습니다.
지금부터는 GAN 알고리즘을 설명하여 어떻게 논리적으로 이루어지는지 살펴보겠습니다.

우선 m개의 노이즈를 샘플링을 진행하고, m개의 원본 데이터를 뽑습니다. 위의 discriminator 같은 경우에 첫 번째 식을 이용하여 학습을 시키고, 생성자의 경우에는 두 번째 식을 이용하여 학습을 진행하게 됩니다.

이를 통해 학습 후 생성한 이미지를 보면 위와 같습니다.
논문에서는 임의로 몇 개를 뽑았으며, 이는 단순 암기를 통한 생성이 아닌 분포를 유사하게 만들어 생성한 이미지라고 말했습니다. 마지막 노란 컬럼은 바로 왼쪽의 이미지를 생성한 이미지로 굉장히 비슷하지만 똑같지는 않음을 보이며 단순 암기가 아님을 보였습니다.
다른 생성모델들에 비해 성능도 좋음을 보이며, auto-encoder 계열의 다른 생성 네트워크와 비교했을 때 blurry하지 않고 sharp한 이미지를 생성함을 보였습니다.

1을 만들 수 있는 latent vector와 5를 만들 수 있는 latent vector 사이에서 interpolating을 진행하며 실제 이미지로 바꿔본 것
생성자에 들어가는 latent space의 공간에서 만들어지는 이미지는 그럴듯한 이미지로 변형되며 사용될 수 있습니다.

참고 : https://www.youtube.com/watch?v=AVvlDmhHgC4