Linear Algebra
2장. Linear transformation and matrix
'Algebra 대수학' 이란 무엇인가?
: 방정식을 어떻게 풀 것 인가에 대해 공부하는 학문
2.1 Linear transformation
V에서 W로 보내주는 변환을 Linear Transformation이라고 한다.
Linear Transformation이 되기 위해서는 T(cx+y) = cT(x)+T(y) 를 만족시키면 된다!
(T(0)=0 를 잘 만족시키는지 주의해야 한다)

Null space : N(T) 란 무엇일까?
Null space는 아래와 같이 T(x)=0이 되는 모든 x를 모아둔 space이다.
Range : R(T) 는?
우리가 아는 치역으로, 정의역 Vector space 내의 원소가 갈 수 있는 모든 image의 집합이다.

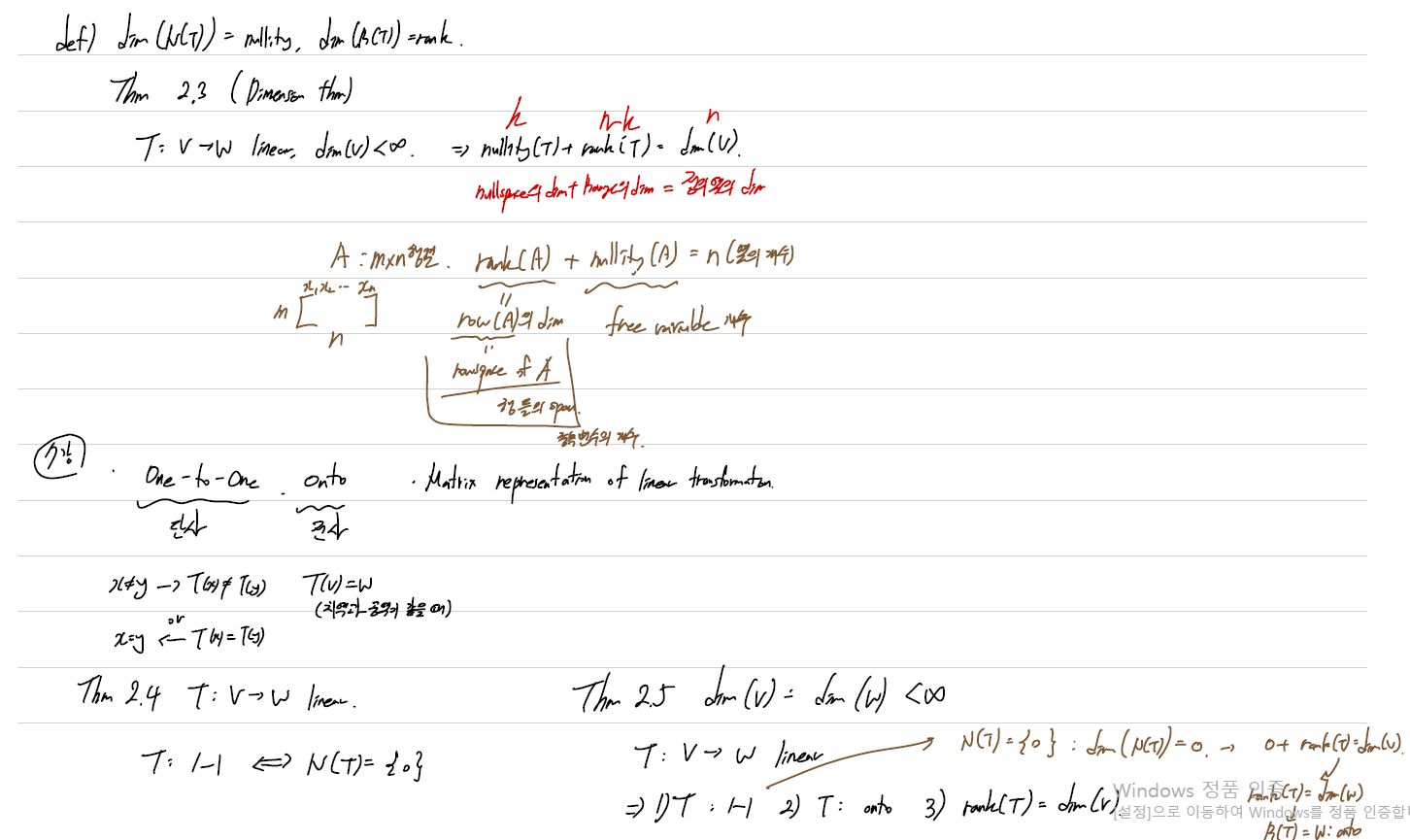
그렇다면 이들의 dimension을 이용한 Nullity와 Rank가 등장한다.
dim(N(T)) = nullity / dim(R(T)) = rank
여기서 아주 중요한 theorem이 등장하는데, 바로 "Dimension Thm" 이다.
=> nullity(T) + rank(T) = dim(V) : 즉, "null space의 dim과 range dim의 합"은 "정의역의 dim"이다!
이를 mxn 행렬로 생각해보자!
(rank(A) = row(A)의 dim) + (nullity(A) = free variable의 개수)
= n(열의 개수)
이제 one-to-one과 onto에 대해 살펴보자.
- one-to-one : 단사
정의역의 임의의 원소 x,y가 x!=y 이면 -> T(x) != T(y) 이다. (대우도 당연히 마찬가지)
T(x) = T(y) -> x = y 이다.
* 1-1 <=> N(T)={0} (zero vector에 대응되는 것이 하나뿐이고 0은 무조건이기에 성립한다) - onto : 전사
T(V)=W로 정의역에서 나간 모든 image의 집합인 치역과 공역이 같을 때 onto라고 한다.
정의역의 basis가 있을 때 공역의 원소들에 대해, there exist one Linear Transformation V to W such that T(vi)=wi for all i
++ linear transformation 에서는 basis에 속하는 vector들의 image가 정해지면, 다른 수 많은 정의역의 vector들의 image도 바로 정해진다! 
2.2 Matrix representation : linear transformation을 행렬로 표현할 수 있다!



2.3 Composition of linear transformation and matrix multiplication



2.4 Invertibility
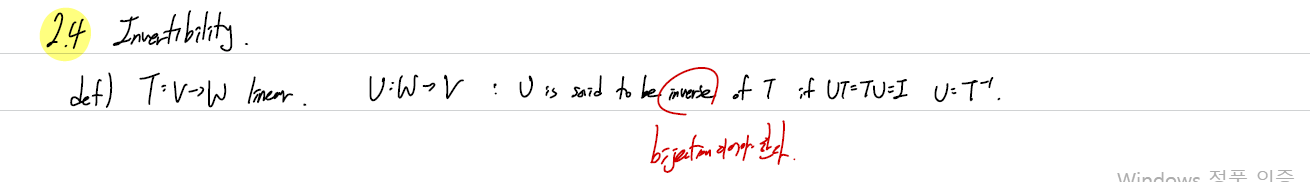


2.5 Change of coordinate matrix

