Linear Algebra

1장. Vector Space

'Algebra 대수학' 이란 무엇인가?
: 방정식을 어떻게 풀 것 인가에 대해 공부하는 학문

1.1 Field

Field는 다양한 조건들을 만족해야 한다.
Field는 수의 집합을 나타내는 개념으로 아래와 같이 closed under additive, multiplication / commutative / associative / there exist additive, multiplicative identity & inverse (mutiple에 대해서는 0 제외) / distributive 를 만족해야 한다.

이러한 조건들을 만족하는 예시로는 실수집합, 유리수 집합, 복소수 집합 등 아래와 같은 많은 Field들이 존재한다.
하지만 당연히 Field가 되지 않는 예시들도 볼 수 있다.
예를 들어 자연수 집합과 정수 집합은 3에 대한 곱의 역원을 가지고 있지 않기에 Field가 될 수 없다.

1.2 Vector Space

Field에 대해 공부했다면 이제 Vector Space에 대해 알아보자
Vector Space는 Field의 원소들로 이루어진 특정 조건들을 만족시키는 대수적 구조로 아래의 조건들을 만족시켜야 한다!!
Vector Space의 예시로는 아래와 같은 많은 경우가 존재하며, 특정 조건을 만족하는지 확인하며 증명해낸다.Vector Space와 관련한 다양한 Theorem들을 보자면,
Thm 1.1 : Cancellation Law 로 등식의 양쪽을 뺄 수 있고, 이에 따른 Corollary로 identity(0)와 inverse의 uniqueness를 확인해 볼 수 있다.
Thm 1.2 는 Field원소와의 연관성으로 연관짓는 값 혹은 도출되어 나온 값이 scalar인지 vector인지 잘 확인해야 한다.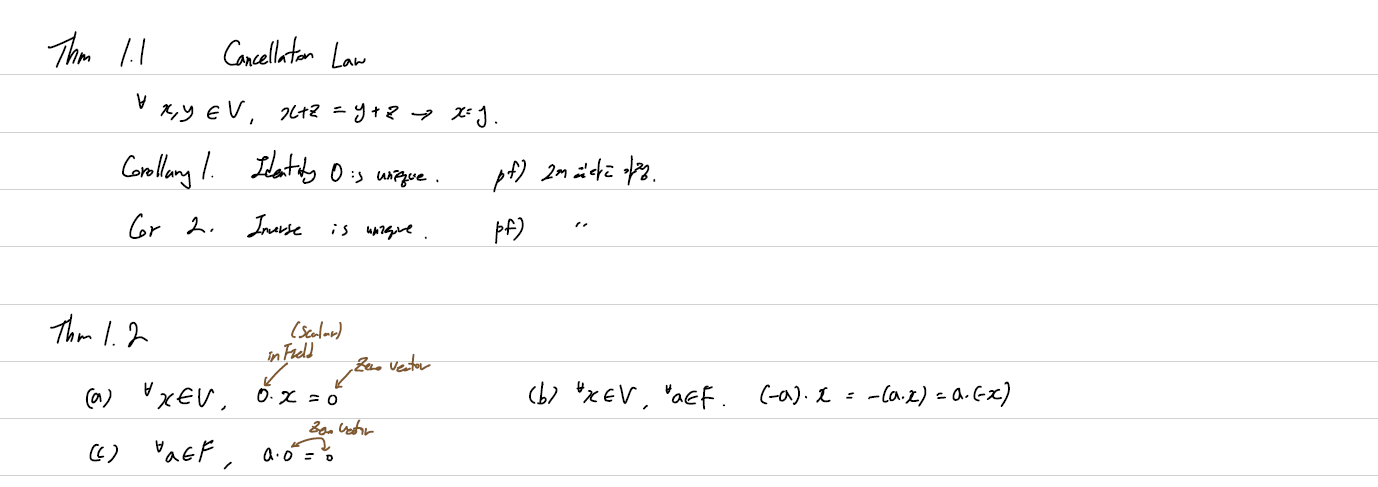

1.3 Subspace

다음은 Subspace에 대하여 알아보자
Subspace는 어떠한 Vector Space의 부분집합이자 Vector Space의 조건들을 만족시키는 공간이다.
부분 공간과 관련한 다양한 Thm들을 아래에서 확인해 볼 수 있다.

1.4 Linear Combination

다음은 Linear Combination으로 vector들 간의 연관으로 이루어진 형태를 의미한다.
아래의 definition과 같이 v는 u1부터 un까지의 linear combination으로 이루어진 vector로 볼 수 있다.
이와 관련하여 Span의 개념도 볼 수 있고, Thm 1.5와 같이 Vector Space의 subset의 span(=생성)은 subspace가 되는 것을 볼 수 있다.
++ span(공집합) = {0}

1.5 Linear Independent / dependent

이제 이러한 내용과 관련하여 1.5 linear independent / dependent가 시작된다.
정의로는 다양한 vector들과 scalar들의 연관으로 이루어진 식에 대해 = 0을 만족시키는 scalar값이 모두 0인 해 밖에 없다면, 이를 linearly independent라고 부른다. 반대로 다른 해가 존재한다면 적어도 어떤 하나의 vector는 다른 vector들로 표현될 수 있기에 linearly dependent라고 말한다.
아래의 Thm 1.7과 같이 재밌는 경우도 확인해 볼 수 있다.

1.6 Bases and Dimension

이제 1장의 마지막 내용이다. 바로 Bases와 dimension에 대해 말해볼 것 인데
basis는 B가 Linearly Independent subset of V(Vector Space)이며, Vector Space V를 Span 한다면 B를 V의 basis(기저)라고 부른다.
++ 위에서 span(공집합) = {0} 이라고 했는데 공집합은 Linearly Independent이며, {0}을 span하기에 {0}의 basis라고 볼 수 있다!!

이에 더하여 아래 Dimension을 볼 수 있는데, 쉽게 말해 dimension은 basis내에 있는 vector의 개수라고 생각하면 된다. 예를 들어 위에 예시를 든 {0}은 공집합의 span이기에 dim은 0이라고 할 수 있다.
만약 dim을 알고 있다면, 무엇을 알 수 있을까?
1) V를 generate하는 vector n개가 있다면 basis이다
2) V의 아무 linearly independent한 n개의 vector를 가져오면 그것이 basis이다

벌써 1장 Vector Space를 마쳤다!!
다음 포스터에서는 2장 Linear transform and matrix에 대해서 알아볼 것이다.