NCF : Neural Collaborative Filtering

논문 리뷰에 앞서 "추천 시스템" 은 무엇이며 이의 필요성과 역사 등에 대하여 이해한다면 이 논문을 읽는 데 많은 도움을 받을 수 있습니다.
추천 글 : NFC를 이해하기 위한 내용 - 추천 시스템이란 무엇인가?

Recommender System

본 논문에서는 Collaborative Filtering에 기반한 대표적인 방법중 하나인 Matrix Factorization(MF)의 한계를 지적합니다. 본 논문을 읽으며 MF의 문제점과 이를 극복한 Neural Collaborative Filtering은 무엇이며, 어떻게 해결하였는지 살펴보겠습니다.

Abstract

• Matrix Factorization(MF)
  

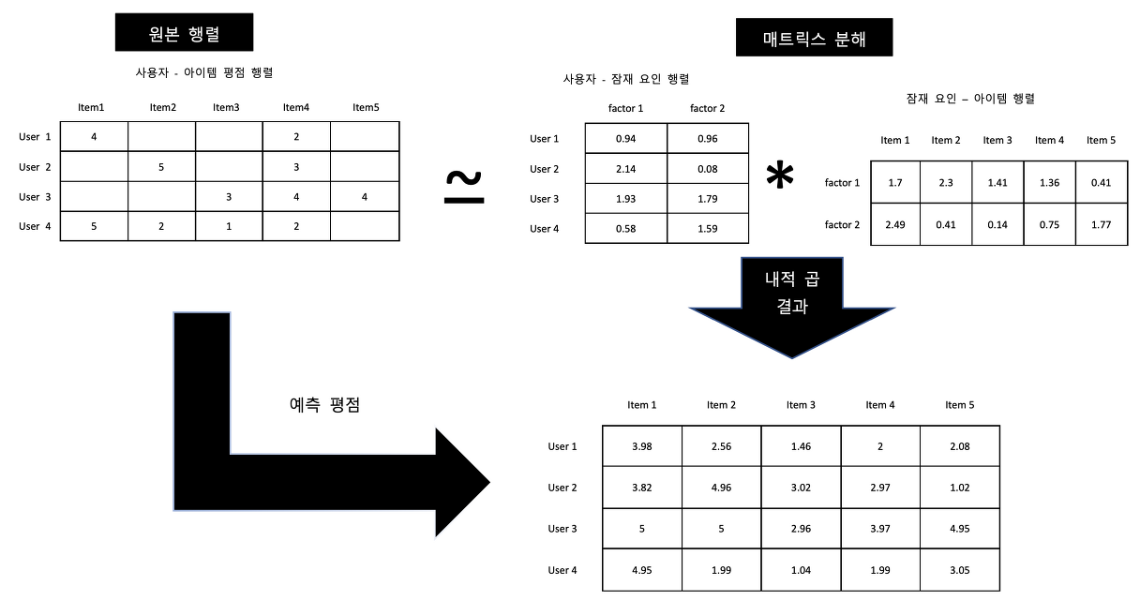
Matrix Factorization(MF)은 추천 시스템에서 널리 사용되는 방법입니다. 이는 user와 item 간의 상호작용을 학습하는 한 방법으로, user-item 공간의 latent feature들의 내적을 통해 두 관계를 표현하게 됩니다.
이에 대하여 Neural Net 기반의 architecture인 Neural Collaborative Filtering(NCF)를 제시함으로 보다 유연한 방식으로 두 관계를 표현할 수 있는 일반화된 MF 모델을 제안합니다.

1. Introduction

위에서 언급한 MF는 선형 방식이기에 user와 item간의 복잡한 관계를 표현하는데 한계가 있습니다. 반면 Deep Neural Network(DNN)의 multi-layer 구조는 non linear하기 때문에 복잡한 구조를 표현하는데 용이합니다.
따라서 논문은 이를 이용하여 user와 item간의 관계를 더욱 유연하게 표현하고자 합니다.

• DNN에 기반한 Collaborative Filtering 방법 제시 : NCF
• MF는 NCF의 특별한 케이스임을 증명
• 다양한 실험을 통한 NCF의 효율성 증명

2. Preliminaries : 사전 지식

2.1 Learning from implicit data

M과 N이 각각 user와 item 개수라고 할 때 user-item행렬 Y는 위와 같습니다. 여기서 y-u,i = 1은 user u와 item i간의 상호작요이 있음을 나타냅니다. 상호작용이란 user가 item을 열람했거나, 구매했거나 등의 암시적인(implicit) 정보를 의미하며, 주의할 점은 이것은 명시적인(explicit) 선호를 뜻 하는 것은 아닙니다.

즉, y-u,i=0은 상호작용이 없는 것이지 해당 item을 비선호한다는 것은 아니다!

이러한 implicit한 정보를 담고 있는 데이터의 문제는 당연히 user의 선호를 분명하게 정의할 수 없다는 것입니다.

ex)
y-u,i=1 : user u와 item i간에 상호작용이 있다. (꼭 선호를 의미하는 것은 아님)
y-u,i=0 : user u가 item i를 꼭 선호하지 않는 것이 아니다. (항목 자체를 모르기에 0이 나타나는 것일 수 있음)

그렇기에 추천은 y-u,i가 1이 될 확률(user u와 item i의 관련 정도)을 예측하는 문제로 귀결될 수 밖에 없습니다. 이는 아래와 같이 표현할 수 있습니다.

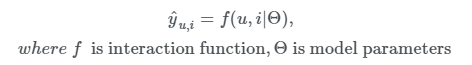
이러한 문제를 해결할 떄 보통 다음과 같은 loss(point wise loss function, pairwise loss function)가 사용되며, 본 논문에서는 모두 이용합니다.

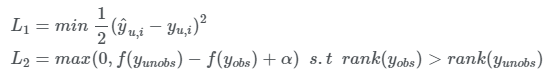
먼저 L1은 point wise loss ft으로 regression 문제에서 많이 사용되며, 실제값과 예측값의 차이를 최소화 합니다.
이와 달리 L2는 pairwise loss ft으로 관측값이 관측되지 않은 값보다는 큰 값을 갖도록하여 두 값의 마진을 최대화합니다.

2.2 Matrix Factorization

위에서 제시한 행렬 Y의 y-u,i를 예측하는 한 가지 방법은 MF를 이용하는 것 입니다. MF는 Y를 행렬 2개로 분해하여 표현하는 방법으로 각 element y_hat은 p_u와 q_i의 내적으로 추정하게 됩니다.

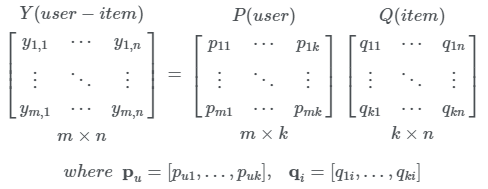
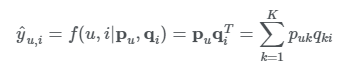
The limitation of Matrix Factorization

하지만 이 MF방식은 한계점이 있습니다. 바로 내적과 같은 linear 모델은 user와 item 간의 복잡한 관계를 표현하는데 한계가 있기 때문입니다.

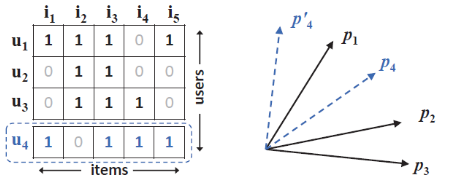
논문의 예시를 들자면 왼쪽 그림과 같은 user과 item간의 행렬이 있다고 할 때, 이를 이용하여 각 user간의 유사도 s_i,j(i와j의 유사도)를 구할 수 있습니다. 그럼 아래와 같은 관계가 성립하는데 이를 기하학적으로 표현하면 위 우측 그림과 같이 표현할 수 있습니다.하지만 여기서 문제가 발생합니다. user 1,2,3를 표현했을 때, 만약 user 4가 들어온다면 아래와 같은 관계로 인해 이를 2차원 상의 벡터로 절대 표현할 수 없습니다.이러한 한계로 인해 user와 item간의 복잡한 관계를 저차원의 단순한 공간에 표현 하는데서 기인합니다. 이에 더하여 linear space는 고정된 특징이 있기 때문에 새로운 관계를 표현하는데 유연하지 못합니다.
따라서 본 논문은 DNN을 이용하여 이러한 문제를 해결합니다.

3. Neural Collaborative Filtering

3.1 General Framework

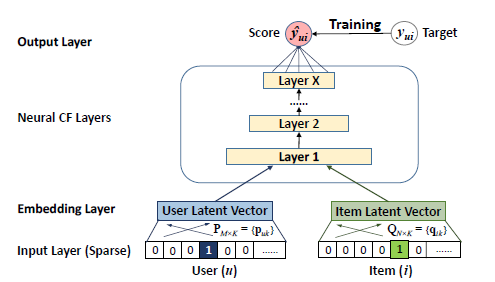
• Input layer (sparse)
  user와 item의 원핫인코딩 벡터가 input으로 사용됩니다.

• Embedding layer
  input에서의 sparse vector를 dense 벡터로 맵핑하는 단계입니다. 보통 dense 벡터를 얻기 위해 임의로 가중치를 초기화 하지만, 별도의 fully connected neural network를 사용할 수도 있습니다.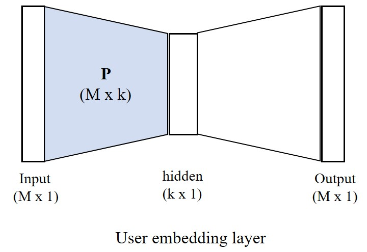
  위를 예로 들자면, user dense vector를 얻기 위한 모델로, 이를 통해 가중치 행렬 P를 얻을 수 있습니다. 이 P는 m차원의 sparse vector를 k(<m)차원의 공간에 projection하는 변환행렬로 볼 수 있습니다. 따라서 이 P 행렬의 각 row는 각 user를 표현하는 저차원의 dense 벡터가 되고 이를 이용해 user latent vector로 사용하게 됩니다.

• Neural CF layers
  이 user latent vector와 item latent vector를 concat한 벡터를 input으로 받아 deep neural network를 통과하는 단계입니다.
  

• Ouput layers
  y.u,i의 추정치인 y hat(user u와 item i가 "얼마나 관련" 있는지)을 구하는 단계입니다. 이 값으 0과 1 사이로 나타나며 ϕout에는 logistic 함수나 prohibit함수를 사용합니다.
  

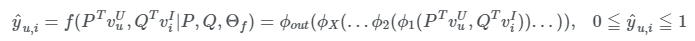
• Learning NCF
  위와 같은 모델을 학습하기 위해서는 앞전에 말한 loss ft을 정의해야 합니다. NCF는 0과 1사이의 예측값을 갖고, 결과 데이터는 0or1로 이진 데이터로 이루어져 있습니다. 일반적으로 이런 분포를 모델링 할 때는 bernoulli distribution을 이용합니다. 즉, Y가 y.u,i=1인 집단을 나타내고, Y-가 0인 집단을 나타낼 때 ,likelihood ft은 아래와 같습니다. 동전 앞뒤를 판단하는 것과 같이 예측값(0과1사이)을 이용한 likelihood ft이라 이해하면 될 것 같습니다.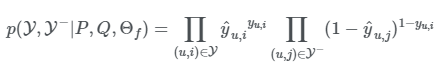
  이어서 loss ft은 아래와 같습니다.(binary cross entropy loss와 동일)
  모델은 이 L을 최소화 하는 파라미터를 찾게 됩니다.
  

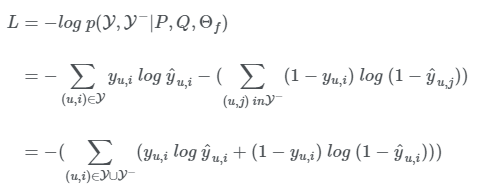
3.2 Generalized Matrix Factorization (GMF)

저자는 앞전에 얘기했던 MF가 이 논문에서 소개하는 NCF의 특별한 케이스임을 보여주며 이를 GMF로 명명합니다.
MF에서는 사용자 벡터와 아이템 벡터의 내적으로 최종 행렬을 만들어 예측했다면, GMF는 각 벡터의 원소마다 가중치를 두어 이를 학습하는 방식입니다. 이러한 GMF에 아래와 같은 a_out, hT, ϕ1를 준다면 이는 MF가 됨을 보이며, MF는 GMF의 특별한 케이스임을 보입니다.

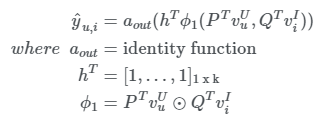
GMF란 a_out과 hT를 아래와 같이 두어 MF를 일반화한 모델입니다. a_out에는 시그모이드 함수를 사용했으며, hT에는 non uniform 값을 주어 내적할 때, 각 텀에 각기 다른 가중치를 주어 latent 벡터의 중요도를 조절하는 역할을 하게 됩니다.

3.3 Multi-layer Percpetron (MLP)

논문에서는 GMF가 linear하고 고정된 특성으로 인해 user과 item간의 복잡한 관계를 표현하지 못하는 반면, 지금 소개할 MLP는 non linear에 flexible하기 때문에 보다 복잡한 관계를 표현할 수 있다고 합니다.

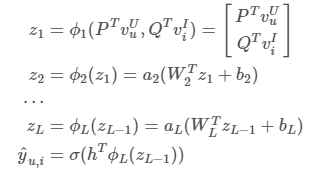
이러한 방식으로 파라미터라이징을 통해 최종 y hat을 구하기 위해 ϕ1부터 ϕL까지 연속적으로 계산이 이루어 집니다. 여기에는 GMF와 달리 ϕ1은 concat, ϕ2~L은 Neural Net 함수로 가중치 행렬 W와 편향벡터 b를 이용한 것을 통해 GMF와 달리 non linear 구조를 확인할 수 있습니다.

3.4 Fusion of GMF and MLP

이 논문에서는 위에 설명한 두개를 통합한 모델을 제시합니다.

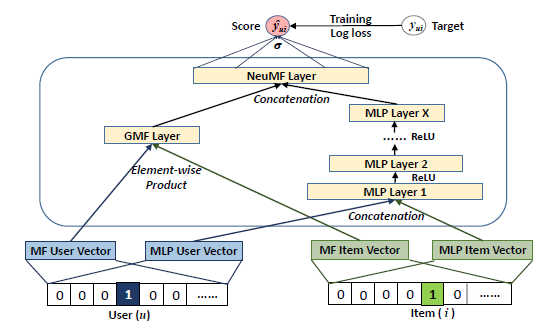
여기서 주목할 점은 각 두 모델별로 서로 다른 embedding layer를 사용한다는 것 입니다. 아래는 모델이 어떻게 파라미터라이징 되는 지 보여주는데, pu^G와pu^M은 각 GMF와 MLP의 user latent vector입니다. 서로 다른 임베딩 layer를 사용하는 의미는 두 벡터의 차원이 다를 수 있다는 것이며, 결국 y hat을 구할 때 concat하기에 차원은 상관이 없음을 확인할 수 있습니다. concat을 진행한 후 h로 가중치를 주고 sigmoid를 통과함에 따라 최종 추정치 y hat을 구하게 됨을 확인할 수 있습니다.

이 모델은 user과 item간의 상호관계를 표현하기 위해 MF의 linearity와 MLP의 non linearity를 결합한 것입니다. 이러한 모델을 논문에서는 Neural Matrix Factorization 이라고 하였습니다.

Conclusion

Neural Matrix Factorization은 GMF와 MLP를 결합한 모델입니다. GMF는 MF를 일반화한 모델이며(linear), MLP는 DNN(deep neural network) 모델(non linear)로, 이 둘을 결합함으로써 linear space에 기반한 기존 모델의 한계점을 극복하고, collaborative filtering의 핵심가치(user와 item의 상호작용 모델링)를 놓치지 않으면서 성능 또한 높일 수 있었음을 확인할 수 있었습니다.

이 방법은 기존 모델들과 아이디어는 비슷하지만 collaborative filtering의 아이디어를 실현한다는 점에서 큰 contribution을 갖습니다